1. 引言
党的十九大指出“不忘初心,方得始终。”高校有义务积极引导学生热爱祖国听党指挥,积极响应国家号召和需求,培养学生增强遵纪守法的意识,帮助学生建立良好的道德情操、积极进取勇于担当的时代精神。作为高校教师,更应牢记自己身上的使命,回答好总书记“为谁培养人、培养什么样的人和怎样培养人”这三个教育的根本问题并落实在自己的教学始终 [1] 。但人生观的建立远非一朝一夕之功,全面健康的人生观仅靠传统的思想政治课堂是远远不够的,而习近平总书记在全国高校思想政治工作会议上的讲话恰恰为我们打开了一扇新的大门。他指出,要用好课堂教学这个主渠道,思想政治理论课要坚持在改进中加强,提升思想政治教育亲和力和针对性,满足学生成长发展需求和期待,其他各门课都要守好一段渠、种好责任田,使各类课程与思想政治理论课同向同行,形成协同效应 [2] 。这一讲话肯定了在专业课课程中融入思政内容的必要性和可行性,为高校教育指明了方向。
课程思政要求各学科授课教师在熟悉本学科专业课程的基础上,还要尽可能地将学科知识与思想政治内容相结合,达到“既育才也育德”的教学要求 [3] [4] 。经过几年的建设,特别是在2018年学校实施“双带头人”后,按照习总书记落实立德树人根本任务的指示,以高质量党建引领学校高质量发展,牢固树立“抓基层、打基础”的理念,不断加强教师党支部建设,大力选配政治素质好、工作能力强、既熟悉党建工作又是业务骨干的优秀教师担任党支部书记,实现支部书记既是党建带头人也是学术带头人的“双带头人”机制,进而促进数学系逐渐形成以教工党支部为依托的课程思政改革。经过一系列的理论与实践研究,在如何确定课程思政教学目标和如何将思政元素有机融入课堂等教学问题上取得了很多宝贵的经验。形成了案例式教学的课程思政模式。
2. 线性代数课程教学目标的确立
在课程思政建设中,始终以总书记“为谁培养人、培养什么样的人和怎样培养人”这三个教育的根本问题为指导思想,依据《高等学校课程思政建设指导纲要》,强调文化自信,突出科学精神、石油精神。通过与线性代数知识相结合 [5] ,使思政的内容有了具体的案例基础,使学生更易接受,更易产生共鸣。将课程思政教学目标设计为以下三点(详见图1):
(1) 引导学生树立文化自信。
(2) 培养学生的科学精神、石油精神和辩证唯物主义世界观。
(3) 帮助学生懂得数学的美和价值。
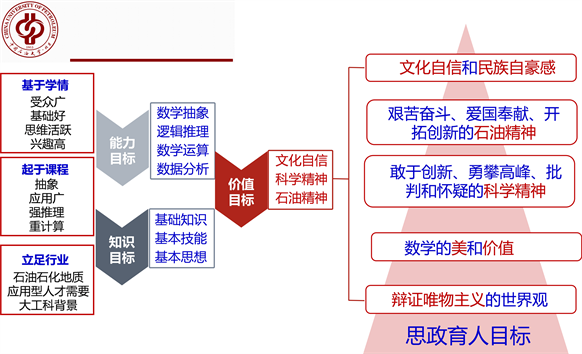
Figure 1. The goals of ideological and political education
图1. 课程思政目标
3. 案例式教学模式的构建
围绕上述育人目标,团队从以下四个方面开展思政建设工作,形成了线性代数案例式教学模式:
(1) 能力建设,提高教师思政素养。团队开展了示范性教学和课程思政教学竞赛等各项活动,鼓励教师积极探索和参与课程思政,让课程思政深入人心,成为教师的自觉行动。
(2) 二次开发,编制课程思政案例。根据知识体系构建了丰富的思政案例库和示范教学课件,积累了丰富的教学素材。
(3) 内容重构,有机融入思政主题。以案例为着力点,重构导入内容,服务思政主题;以科技话题为载体,重构例题,强化思政主题。
(4) 多管齐下,助力思政落地生根。线上与线下相结合,增加课程与学生之间的粘性;增加互动式、发现式和研讨式教学,提高学生的主动性和参与度;运用雨课堂、学习通等智慧教学工具进行教学管理和反馈改进,在跟踪过程中推动思政落地。
经过多年的建设,课程团队梳理汇总了线性代数中能够融入课程思政的知识点以及适合融入到线性代数课堂的思政内容,以科学精神和石油精神为着力关键,以专业伦理与社会服务为价值依托,不生硬、不刻意,做到“润物细无声”。两项结合共编制出10个线性代数课堂思政案例 [6] ,见表1。每个案例都实现了“如春在花,如盐在水”般的效果。
4. 课程思政案例展示
4.1. 穿越千年的科技之光——从《九章算术》增强学生的文化自信和民族自豪感
高斯消元法是用矩阵解线性方程组的一种方法,形成于19世纪初,其基本思想是分离系数,顺序消元。由于这一方法有明确、清晰的计算程序,所以它是用电子计算机解线性方程组常用的一种方法。事实上这个解法早在中国古代数学著作《九章算术》中就已出现,虽较新法略繁,但步骤整齐,算法别致,和高斯消元法有颇多相似之处。

Table 1. Cases of ideological and political education
表1. 课程思政案例汇总
《九章算术》成书于东汉初年(公元一世纪),刘徽重辑《九章算术》是在公元263年,比欧洲早了一千多年。《九章算术》中使用筹算求解三元一次线性方程组时,去掉未知数,将系数和常数项都放在固定的位置上,可以说是构成一个图表。若把筹算的图表“看作”矩阵,其转置即为方程组的增广矩阵。筹算的“遍乘”是用一个非零数乘方程的各项,筹算的直除法是从一个方程累减(或累加)另一个方程,这实际上就是对方程组的增广矩阵进行初等行变换。无论是从运算过程还是从结果的形式上看,两者是一致的。
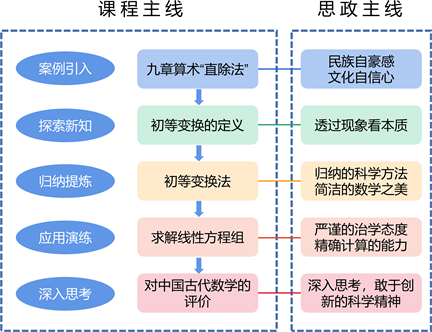
Figure 2. Teaching design of ideological and political education for case 1
图2. 案例1课程思政教学设计
通过对比讲解的教学方式(见图2),使学生认识到数学体系的建立承载了先辈们锲而不舍的钻研,只有勇于深入探索,不断完善,才能攀登科学高峰。在培养学生探究精神和创新思维的同时,更提升了文化自信和民族自豪感。课堂效果反馈时学生们纷纷表示:先辈们的突出成就是如今发展的基石,未来将在科技创新中继续努力,书写新的历史篇章。
4.2. 从病态方程组问题培养学生的科学精神
在第三章线性方程组的解一节已经完全解决了线性方程组问题,即:可以根据系数矩阵的秩和增广矩阵的秩确定线性方程组解的存在性、唯一性以及如何求解。但完美的理论应用到实际仍然会出现问题。
第一个问题由伏安法测电阻引出。实验时通过调节滑动变阻器,可以得到几组电流和电压的值。将这些值代入欧姆定律,就得到方程组(1)
(1)
由定理可知,方程组(1)是矛盾方程组,无解;但一个电阻的阻值又是客观存在的。这里可引导学生讨论出现这一问题的原因,并结合伏安法测电阻的实验步骤分析如何从矛盾方程组中求出“客观存在的解”。最后由老师总结:出现这个问题的原因就是由于误差的普遍存在性,因此需要经过多次测量以求最大程度减少测量误差。工程上,这一类方程数量大于未知数数量的方程组叫做超定方程组。实验时,在伏安坐标纸上画过原点的直线,这条直线的斜率就是电阻的阻值,其实这就是最小二乘法,即虽然不能满足每个方程,但我们选取的解应保证每个方程左右两边的差别尽量小。运用最小二乘法解决伏安法测电阻的问题,就是理论应用到实际时遇到的问题,也就是解的判定定理在解决线性方程组解的存在性上遇到的实际问题。培养学生以科学的态度看待问题、评价问题,求真务实,开拓创新,注重实践,勇于探索。
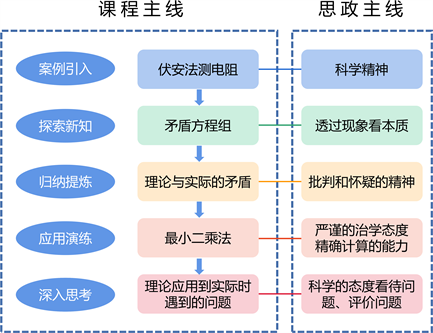
Figure 3. Teaching design of ideological and political education for case 2
图3. 案例2课程思政教学设计
第二个问题是解的稳定性。在授课过程中首先给出下面两个线性方程组并求解。
(2.1)
(2.2)
方程组(2.1)和(2.2)的系数矩阵完全一样,常数项差别很小,可以看作是对同一实验的两次测试结果,然而两者解的差别却特别大,这种方程组的参数有微小改变导致解的差别特别大的线性方程组是不稳定性的。此时用近似方程组得到的解是没有办法代替原方程组解的。然而不稳定方程组在工程实际中大量存在,因此如何从近似方程组中找到某种“合理的解”来代替原方程组的解一直是研究者们热衷的问题。经过很多专家学者几十年的努力,目前已经获得了一系列的办法,然而解的稳定性这个问题依然没有完全解决。
在课堂教学中,直面这一“未能解决”的问题,激发学生的好奇心和学习热情,鼓励学生积极探索适当的方法让理论知识在实践中发挥最大作用。在探索过程中培养学生大胆猜想、小心求证的批判和怀疑的精神,树立理论联系实际、实践是检验真理的唯一标准等科学思想,强调注重实践等科学精神(见图3)。并通过两个实例引出实际与理论的差别,引导有兴趣的同学继续阅读相关文献,培养自主学习的能力。
5. 总结
线性代数课程作为一门起点低、受众面广的公共数学基础课程,蕴含了丰富的思政元素和哲学思想,是开展课程思政教学的良田沃土。课程团队从历史、特性、案例和相关知识点出发梳理思政元素,建设教学案例,设计教学方法,将思政教育有机地融入教学过程,力求将立德树人的教育目标融入日常教学的点点滴滴。
尽管已取得初步成效,但线性代数课程思政建设仍然任重道远。在今后的课程建设中,团队将继续融会创新,紧跟时代发展,捕捉课程知识与思政元素的新结合点,不断拓展线性代数课程思政建设的方法和途径,丰富完善教学案例库,与学生在“思政”中共同成长。
致谢
本文由以下项目支持:2017年度教育部人文社会科学研究专项任务(中国特色社会主义理论体系研究)项目“微域网络思政教育探索与实践”(项目批准号:17JD710097)、北京市社会科学基金项目暨2018年度首都大学生思想政治教育重点课题“辅导员全程全方位育人平台建设及实效性研究——基于移动学习分析技术视角”(项目批准号:17KDB034 BJSZ2018ZD07)、中国石油大学(北京)本科一般教改项目“依托教工党支部,构建《线性代数》课程思政体系”。
NOTES
*通讯作者。