不同拓扑结构下无线传感器网络可靠性模型

Reliability Models of Wireless Sensor Networks with Different Topologies

摘要: 无线传感器网络系统的拓扑结构种类繁多，节点连接方式不尽相同，在不同场景下往往会采用不同的拓扑结构模型。因此，探究不同拓扑结构下无线传感器网络的可靠性模型尤为必要。本文采用串联、并联以及连续k/n(G)系统等典型系统作为案例，在系统中各节点失效独立的条件下，构建无线传感器网络系统的可靠度一般模型，讨论在系统中各节点寿命分布均服从于Weibull分布，且尺度参数不变时，系统可靠度在不同形状参数下的变化趋势，并结合案例进行计算。结果表明，串联系统的可靠度低于并联系统和连续k/n(G)系统，当节点寿命分布的形状参数大于1时，系统具有较高的可靠性；当系统中的节点数相同时，环型拓扑网络系统的可靠度最弱。

Abstract: There are many kinds of topologies of wireless sensor network systems, the node connection meth-ods are different, and different topology models are often used in different scenarios. Therefore, it is necessary to explore the reliability model of wireless sensor networks under different topologies. In this paper, a typical system such as series, parallel and continuous k/n(G) systems are used as ex-amples, under the condition that each node in the system fails independently, a general model of the reliability of the wireless sensor network system is constructed, and the variation trend of the reliability of the system under different shape parameters is discussed when the life distribution of each node in the system is subject to the distribution and the scale parameters remain unchanged, and the case is calculated. The results show that the reliability of the series system is lower than that of the parallel system and the continuous k/n(G) system, and the system has higher reliability when the shape parameter of the node life distribution is greater than 1. When the number of nodes in the system is the same, the reliability of the ring topology network system is the weakest.

1. 引言

无线传感器网络(Wireless Sensor Networks, WSN)是一种分布式传感网络，它由大量的传感器节点所组成，这些节点大量随机部署在被监测区域，主要作用是完成对周围环境中所需要数据的感知、处理和传输 [1] 。无线传感器网络具有灵活性、容错性以及快速部署等特点，使其广泛应用在环境、食品、工业等领域，被认为是二十一世纪最重要的技术之一 [2] 。目前，无线传感器网络已在军事国防、工业控制、抢险救灾、环境监测、精准农业等领域中得到成功应用 [3] 。大多数应用都要求无线传感器网络具有高可靠性，因为WSN的故障可能会导致严重后果，如环境污染、经济损失、人员伤亡等 [4] 。随着人们的日常活动和信息交换对WSN的依赖性的增加，如何量化WSN的执行能力，已成为主要关注的问题之一。

目前已有大量文献对系统拓扑结构可靠性进行了研究，但对在不同拓扑结构下的无线传感器网络可靠性模型研究还并不多见。Ju Xiao等人 [5] 利用可靠性理论和数值模拟对不同拓扑结构下的两级级联无源光网络保护策略进行了研究。Tsao等人 [6] 基于价值可靠性评估理论，通过对不同拓扑结构的配电系统可靠性与成本价值分析，得到最合适的系统设计。Mustafa等人 [7] 使用适当的可靠性指标对并网光伏系统在不同拓扑结构下的可靠性模型进行研究。Chakraborty [8] 研究了多状态节点无线传感器网络的可靠性，提出了用于评估多状态传感器节点的网络可靠性方法，所提方法在不同拓扑结构上具有高度适用性。谢果丰 [9] 探究了相关失效对不同系统结构的系统可靠性影响，并利用算例探讨Copula对不同部件数的系统可靠度影响。Basaran等人 [10] 从网络可靠性的角度，研究了具有非结构化拓扑结构的无线网络的中断性能。Habashneh等人 [11] 概述了基于系统可靠性的结构拓扑优化的最新进展、增强与应用，优化拓扑结构找到各节点连接的最佳方式对系统的性能有重大影响。郄鑫等人 [12] 以典型电网为例建立了系统拓扑仿真算例，分析了在不同拓扑调整方法下，短路电流抑制效果和对系统可靠性的影响。

综上所述，对无线传感器网络的可靠性进行研究，设计并利用合适的可靠性模型与可靠性分析方法，来分析无线传感器网络的可靠性，对于降低无线传感器网络的故障风险以及减少或避免故障发生时造成的损失具有重要的意义。基于此，本文在系统中各节点失效独立的假设下，构建无线传感器网络系统的可靠度一般模型，即WSN系统中的每个节点是相互独立的，每个节点的失效都不会导致其它节点发生故障。该假设对简化系统分析和可靠性建模具有较大的帮助，尤其适用于系统结构相对简单、节点间相互影响较低的情况，有助于提供清晰且可推导的数学模型。同时，在对WSN系统可靠性有较高要求和资源受限的情况下，假设系统中各节点的失效独立，为WSN系统的设计提供了更为直观的分析框架。

2. 系统可靠性模型

2.1. 串联系统可靠性模型

系统内部每一个节点、模块通过串行的方式构成的系统称为串联系统，在系统运行的过程中，每个节点或模块都必须保持功能正常，系统才能保持正常运行。利用可靠性框图(Reliability Block Diagram, RBD)来表示串联系统，如图1所示：

Figure 1. RBD of series system

图1. 串联系统的 RBD

在一个存在n个普通节点串联系统中，设簇头在t时刻的可靠度为 $R_1\left(t\right)$ ，普通节点在t时刻的可靠度为 $R_2\left(t_i\right)$ ， $\left(i=1,2,3,\cdots ,n\right)$ ，对应的失效分布函数分别为 $F_1\left(t\right)$ 、 $F_2\left(t_i\right)$ ，则各节点可靠度为 $R\left(t_i\right)=1-F\left(t_i\right)$ 。串联系统在t时刻能正常工作的条件是系统中所有的节点都能正常工作，若系统中各节点失效相互独立，则处于t时刻的串联系统可靠度为：

$R=R_1\ast {\displaystyle \underset{x=1}{\overset{n}{\prod }}{R}_2\left(t_x\right)}$ (2-1)

失效率曲线是用于讨论可靠性的典型概念，按硬件失效的发生时间，硬件失效率曲线可分为三个不同阶段：早期、稳定期和消耗期，曲线的形状呈现出两头高，中间低的浴盆状趋势，如图2所示，具有明显的阶段性。Weibull分布是可靠性工程领域中使用范围最为广泛的其中一种寿命分布，采用不同的参数时，可以得到不同的失效模式，能很好的展示出硬件失效的“浴盆曲线”特征。因此，为了验证利用本文模型所构建的WSN系统可靠性，本文假设WSN系统中的每个节点寿命均服从于式(2-2)的Weibull分布，但普通节点和簇头的寿命分布参数可以不同，其可靠性函数如式(2-3)所示。

$G\left(t\right)=1-\exp \left(-{\left(\frac{t}{\lambda }\right)}^k\right)$ (2-2)

$R\left(t\right)=1-G\left(t\right)=\exp \left(-{\left(\frac{t}{\lambda }\right)}^k\right)$ (2-3)

其中， $\lambda$ 为尺度参数，k为形状参数。

Figure 2. Typical hardware failure rate curve

图2. 典型硬件失效率曲线

若假设在一个串联系统中，共包含5个普通节点和一个簇头，且普通节点和簇头的寿命分布均服从于Weibull分布，由于串联系统只有在簇头和普通节点全部正常工作情况下，才能正常运行。此时，系统的可靠度为如式(2-4)所示，变化趋势如图3所示。

$R\left(t\right)=R_1\ast {\left(R_2\right)}^5=\exp \left(-{\left(\frac{t}{{\lambda }_1}\right)}^{k_1}\right){\left[\exp \left(-{\left(\frac{t}{{\lambda }_2}\right)}^{k_2}\right)\right]}^5$ (2-4)

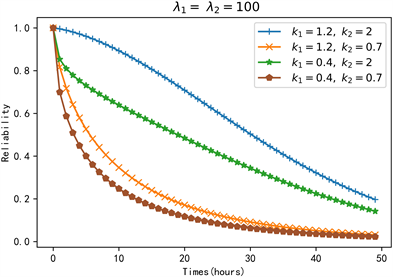
Figure 3. Variation trend of reliability function of series system

图3. 串联系统的可靠度函数变化趋势

2.2. 并联系统可靠性模型

系统内部每一个节点、模块通过并行的方式构成的系统称为并联系统，在并联系统中一条或某几条通路的失效不影响系统的正常运行，至少一条通路保持正常运行系统都不会发生失效，并联结构可靠性框图示意图如图4所示：

Figure 4. RBD of parallel system

图4. 并联系统的RBD

在一个存在n个普通节点并联系统中，设簇头在t时刻的可靠度为 $R_1\left(t\right)$ ，普通节点在t时刻的可靠度为 $R_2\left(t_i\right)$ ， $\left(i=1,2,3,\cdots ,n\right)$ ，对应的失效分布函数分别为 $F_1\left(t\right)$ 、 $F_2\left(t_i\right)$ ，则各节点可靠度为 $R\left(t_i\right)=1-F\left(t_i\right)$ 。并联系统在t时刻能正常工作的条件是系统中至少有一个普通节点是正常工作的，若系统中各节点间相互独立，则处于t时刻的并联系统可靠度可表示为：

$R=1-\left(\left(1-R_1\left(t\right)\right)+R_1\left(t\right){\displaystyle \underset{x=1}{\overset{n}{\prod }}\left(1-R_2\left(t_x\right)\right)}\right)$ (2-5)

若假设在一个并联系统中，共包含5个普通节点和一个簇头，且普通节点和簇头的寿命分布分别服从于式(2-2)的分布，则当该系统中至少有一个普通节点能正常工作时，系统能正常运行。此时，系统的可靠度如式(2-6)，变化趋势如图5所示。

$\begin{array}{c}R\left(t\right)=1-\left(\left(1-R_1\left(t\right)\right)+R_1\left(t\right){\displaystyle \underset{x=1}{\overset{5}{\prod }}\left(1-R_2\left(t_x\right)\right)}\right)\\ =1-\left\{\left[1-\exp \left(-{\left(\frac{t}{{\lambda }_1}\right)}^{k_1}\right)\right]+\exp \left(-{\left(\frac{t}{{\lambda }_1}\right)}^{k_1}\right){\left[1-\exp \left(-{\left(\frac{t_x}{{\lambda }_2}\right)}^{k_2}\right)\right]}^5\right\}\end{array}$ (2-6)

Figure 5. Variation trend of reliability function of parallel system

图5. 并联系统的可靠度函数变化趋势

2.3. 表决系统可靠性模型

存在一类系统结构，在其组成的节点或模块数量为n的基础上，系统内必须至少有k个节点或模块正常工作，系统才能正常运转，换句话说，系统故障部件数量如果大于 $n-k+1$ ，系统才会发生整体性失效，符合这样失效机制的系统在可靠性领域称为表决系统，即k/n(G)系统。利用可靠性框图来表示k/n(G)系统，如图6所示。

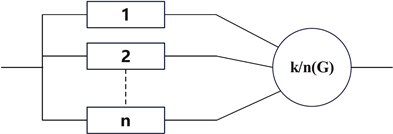
Figure 6. RBD of continuous k/n(G) system

图6. 连续k/n(G)系统的RBD

在一个k/n(G)系统中，若至少有 $n-k+1$ 个普通节点无法正常工作，则系统失效。根据定义，假设 $X_1,X_2,\cdots ,X_n$ 为n个节点的寿命，各节点之间保持相互独立，每个普通节点的可靠度均为 $R_2\left(t_i\right)$ ，则系统可靠度为：

$R=R_1\ast {\displaystyle \underset{x=\left[k\right]}{\overset{n}{\sum }}{C}_n^x}{\left[R_2\left(t_i\right)\right]}^x{\left(1-R_2\left(t_i\right)\right)}^{n-x}$ (2-7)

若假设在一个k/n(G)系统中，共包含5个普通节点和一个簇头，且普通节点和簇头的寿命分布分别服从于式(2-2)的分布，由于k/n(G)网络系统的可靠度与普通网络的有效节点的覆盖率有关，因此，在簇头节点正常工作情况下，当该系统中能正常工作的普通节点数量不小于3时，系统能正常运行。此时，系统的可靠度如式(2-8)，变化趋势如图7所示。

$\begin{array}{c}R\left(t\right)=1-F_1\left(t\right)-F_2\left(t\right)=R_1\left(t\right){\displaystyle \underset{x=3}{\overset{5}{\sum }}{C}_5^x}{\left[R_2\left(t\right)\right]}^x{\left[1-R_2\left(t\right)\right]}^{5-x}\\ =\exp \left(-{\left(\frac{t}{{\lambda }_1}\right)}^{k_1}\right){\displaystyle \underset{x=3}{\overset{5}{\sum }}{C}_5^x}{\left[\exp \left(-{\left(\frac{t}{{\lambda }_2}\right)}^{k_2}\right)\right]}^x{\left[1-\exp \left(-{\left(\frac{t}{{\lambda }_2}\right)}^{k_2}\right)\right]}^{5-x}\end{array}$ (2-8)

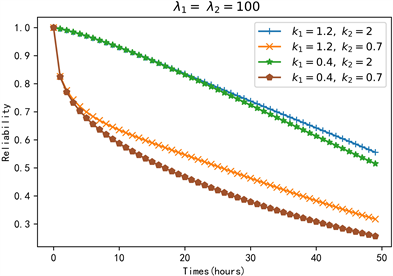
Figure 7. Variation trend of reliability function of k/n(G) system

图7. k/n(G)系统的可靠度函数变化趋势

结合三种系统的可靠度变化趋势来看，在尺度参数不变的情况下，当WSN系统内的节点寿命分布均服从形状参数k大于1的Weibull分布时，WSN系统具有较高的可靠性。这是因为当 $k>1$ 时，Weibull分布的可靠性函数 $R\left(t\right)$ 如式(2-3)所示，与时间t呈负相关，即递减风险的特性，这表示无线传感器网络系统在初期具有较低的失效概率。同时，从概率密度的角度来看，较大的形状参数k意味着节点寿命分布的尾部更重，即系统有更高的概率具有较长的寿命，增加了无线传感器网络系统在长时间内保持正常运行的可能性。

3. 不同拓扑结构的可靠性模型

3.1. 星型拓扑结构可靠性模型

星型拓扑结构如图8所示，网络中的各节点通过点到点的方式连接到一个汇聚节点上，由该汇聚节点向目的节点传送信息。星型网络为典型的k/n(G)系统，在该系统中，各个普通节点分别与汇聚节点相连接，在汇聚节点和不少于[k]个普通节点都能正常工作的情况下，该系统才能正常运行。

Figure 8. Star topology

图8. 星型拓扑结构

假设星型拓扑结构的汇聚节点可靠度为 $R_1\left(t\right)$ ，第i个普通节点的可靠度为 $R_2\left(t\right)$ ，且该系统为k/n(G)系统，在各节点失效独立的假设下，星型拓扑结构系统失效概率如式(3-1)所示。

$F\left(t\right)=F_1\left(t\right)+\left[1-F_1\left(t\right)\right]{\displaystyle \underset{x=n-\left[k\right]+1}{\overset{n}{\sum }}{C}_n^x}{\left[F_2\left(t\right)\right]}^x{\left[1-F_2\left(t\right)\right]}^{n-x}$ (3-1)

星型拓扑结构的系统可靠度可由式(3-2)表示。

$R\left(t\right)=1-F\left(t\right)=R_1\left(t\right){\displaystyle \underset{x=\left[k\right]}{\overset{n}{\sum }}{C}_n^x}{\left[R_2\left(t\right)\right]}^x{\left[1-R_2\left(t\right)\right]}^{n-x}$ (3-2)

若在t时刻，该系统的 $R_1\left(t\right)=0.95$ ， $R_2\left(t\right)=0.9$ ，则系统的可靠度为：

$\begin{array}{c}R\left(t\right)=R_1\left(t\right){\displaystyle \underset{x=3}{\overset{n=5}{\sum }}{C}_5^x}{\left[R_2\left(t\right)\right]}^x{\left[1-R_2\left(t\right)\right]}^{5-x}\\ =0.95\times \left[C_5^3\times {0.9}^3\times {0.1}^2+C_5^4\times {0.9}^4\times 0.1+{0.9}^5\right]\\ =0.941868\end{array}$ (3-3)

3.2. 网状型拓扑结构可靠性模型

网状型拓扑结构主要指各节点通过传输线互联连接起来，并且每一个节点至少与其他两个节点相连，节点之间可能会存在于回路，拓扑结构如图9所示。在该网络中可能会同时存在串联、并联以及k/n(G)系统。

Figure 9. Mesh topology

图9. 网状型拓扑结构

因为在网状型拓扑结构网络中，线路的连接方式存在多种情况，故无法构建适用于所有网状型拓扑结构的系统可靠性模型。但可以构建适用于像全连接型和环型等特殊网状型拓扑结构的系统可靠性模型。

3.2.1. 全连接型拓扑结构可靠性模型

在全连接型拓扑结构中，每个节点和网络上的其它所有节点都有通信线路连接，每个节点上的信息都可以通过线路传输给其它任意节点。其拓扑结构如图10所示，相比于星型拓扑结构，全连接型网络结构更复杂，但本质上仍为k/n(G)网络系统。

Figure 10. Fully connected topology

图10. 全连接型拓扑结构

在全连接型拓扑结构系统中，假设汇聚节点的可靠度为 $R_1\left(t\right)$ ，第i个普通节点的可靠度为 $R_2\left(t\right)$ ，且该系统为k/n(G)系统，在各节点失效独立的假设下，系统失效概率如式(3-4)所示。

$F\left(t\right)=F_1\left(t\right)+\left[1-F_1\left(t\right)\right]{\displaystyle \underset{x=n-\left[k\right]+1}{\overset{n}{\sum }}{C}_n^x}{\left[F_2\left(t\right)\right]}^x{\left[1-F_2\left(t\right)\right]}^{n-x}$ (3-4)

全连接型拓扑结构的可靠性可由式(3-5)表示。

$R\left(t\right)=1-F\left(t\right)=R_1\left(t\right){\displaystyle \underset{x=\left[k\right]}{\overset{n}{\sum }}{C}_n^x}{\left[R_2\left(t\right)\right]}^x{\left[1-R_2\left(t\right)\right]}^{n-x}$ (3-5)

若一个全连接型拓扑结构网络的 $R_1\left(t\right)=0.95$ ， $R_2\left(t\right)=0.9$ ，且存在7个普通节点和一个汇聚节点，在 $k/n\ge 60\%$ 的情况下，该网络系统可以正常运行。此时，系统的可靠度为：

$\begin{array}{c}R\left(t\right)=R_1\left(t\right){\displaystyle \underset{x=5}{\overset{n=7}{\sum }}{C}_7^x}{\left[R_2\left(t\right)\right]}^x{\left[1-R_2\left(t\right)\right]}^{7-x}\\ =0.95\times \left[C_7^5\times {0.9}^5\times {0.1}^2+C_7^6\times {0.9}^6\times 0.1+{0.9}^7\right]\\ =0.925593\end{array}$ (3-6)

3.2.2. 环型拓扑结构可靠性模型

环型网络的拓扑结构较为特殊，在该网络中，发送端所发出的数据，可延环绕行一周后回到发送端，且任何一个节点发出的数据都可以被环上的其他节点接收到。其拓扑结构如图11所示。环型网络可看作串联系统，需要所有普通节点的信息均能传输至汇聚节点中。

若环型网络拓扑结构中，汇聚节点的可靠度为 $R_1\left(t\right)$ ，第i个普通节点的可靠度为 $R_2\left(t\right)$ ，在各节点失效独立的假设下，环型拓扑结构系统的失效概率可如式(3-7)表示。

$F\left(t\right)=\left[1-F_1\left(t\right)\right]\left[1-{\left(1-F_1\left(t\right)\right)}^n\right]+F_1\left(t\right)$ (3-7)

Figure 11. Ring topology

图11. 环型拓扑结构

环型拓扑结构的系统可靠度可由式(3-8)表示。

$R=R_1\ast {\displaystyle \underset{x=1}{\overset{n}{\prod }}{R}_2\left(t_x\right)}$ (3-8)

例如，当环型拓扑结构网络中的 $R_1\left(t\right)=0.95$ ， $R_2\left(t\right)=0.9$ ，且普通节点的数量为5时，系统的可靠度可表示为：

$R\left(t\right)=R_1\ast {\displaystyle \underset{x=1}{\overset{5}{\prod }}{R}_2\left(t_x\right)}=0.95\times {0.9}^5=0.560966$ (3-9)

4. 总结与展望

4.1. 研究内容总结

无线传感器网络系统的拓扑结构影响着网络的连接性、数据的传输效率以及系统的可靠性。因此，探究不同拓扑结构下无线传感器网络的可靠性模型尤为必要。本文在系统中各节点失效独立的条件下，对无线传感器网络的系统可靠性进行了评估，主要研究内容与结论如下：

1) 选用串联、并联以及连续k/n(G)系统等三类典型系统作为案例，推导出无线传感器网络系统的可靠性一般表达式，并在系统中各节点寿命分布均服从于Weibull分布时，讨论了形状参数对无线传感器网络可靠度的影响。结果表明，串联系统的可靠度低于并联系统和表决系统，当系统内的节点寿命分布均服从形状参数k大于1的Weibull分布时，系统具有较高的可靠性。

2) 推导出了不同拓扑结构下无线传感器网络可靠性模型的一般表达式，并列举了相应的案例对不同拓扑结构下的无线传感器网络系统可靠性进行了求解。结果表明，在不同拓扑结构中，由于环型拓扑网络结构只有在所有节点都不发生失效时，系统才能正常工作，故其系统可靠度最弱。

4.2. 前景展望

本文主要讨论了在系统中各节点失效独立的情况下，不同拓扑结构下的无线传感器网络模型，下一步的研究工作可在现有结论上进行深入讨论，研究方向可分为以下几个方面：

1) 在实际应用中，无线传感器网络可能同时存在多种拓扑结构的混合情况，下一步可以探索混合星型、环型、全连接型等拓扑结构下的可靠性模型，以更全面地分析无线传感器网络系统的性能。

2) 本文在WSN系统中的所有节点失效独立的假设下构建了系统可靠性模型，然而在实际的应用中，无线传感器网络的各系统节点有可能存在节点失效相依的情况，下一步可考虑相关性对系统可靠性的影响规律。

基金项目

国家自然科学基金资助项目(72361008)。