基于端节点部分分量辅助的星型网络中央节点跟踪控制

Central Node Tracking Control of Star Networks via Partial Components Assistance of Terminal Nodes

摘要: 讨论了一类星型复杂动态网络通过端节点的部分分量辅助中央节点实现中央节点的跟踪控制问题。此类星型网络由具有不同状态维数的节点构成，控制器仅施加于中央节点上。在给定中央节点跟踪目标的情况下，为端节点设计辅助跟踪目标，并结合控制理论和稳定性理论，提出自适应控制策略使星型网络的中央节点在控制作用下实现跟踪。所提出的跟踪控制策略的有效性和正确性，既从理论上进行了严格证明，也通过数值仿真进行了验证。

Abstract: The tracking control of the central node assisted by the partial components of the terminal nodes for a class of star complex dynamical networks is discussed in this paper. The star network in this paper consists of nodes with different state dimensions, and the controller is applied only on the central node. Given the tracking target of the central node, the auxiliary tracking targets are de-signed for the terminal nodes and the adaptive control strategy is proposed to guarantee the cen-tral node of the star network realizing tracking based on the control theory and stability theory. The validity and correctness of the proposed tracking control strategy are rigorously proved theoreti-cally and also verified by numerical simulations.

1. 引言

复杂动态网络由节点和连接这些节点的边组成，在实际网络中，每一个个体可视为节点，个体之间的关系可视为节点间的边 [1] 。星型网络作为复杂动态网络中一类简单的规则网络，它是以中央节点为中心，由中央节点和若干端节点(外围节点)相连构成的网络 [2] ，其具有易于管理、集中控制的优点。现有关星型网络的应用越来越多 [2] - [9] ，例如文献 [2] 借助离散事件网络仿真器3对星型拓扑下分布式无人战车与长期演进无线基站通信的网络性能进行仿真分析，文献 [6] 讨论了星型网络中耦合振子的同步优化问题，文献 [9] 借助旋转周期解理论探讨了星型网络结构对同步的影响。

在现有文献中，关于复杂动态网络跟踪问题的研究 [10] - [15] 有很多，例如：在多智能体跟踪研究中，把领导者作为目标信号，所有跟随者的状态需要跟踪上领导者的状态 [10] ，群体无人机系统的轨迹跟踪 [11] 等等。值得注意的是，文献 [11] [12] [13] [14] [15] 探讨的跟踪，是网络在实现跟踪时，每个节点都有一个跟踪目标。而在诸如团队合作、集团作战等现实问题对应的星型网络中，常常最终的目标由中央节点(项目负责人、主机等)完成，但中央节点最终目标的实现需要团队中各个成员即端节点的辅助，且端节点需要完成各自的任务(端节点的跟踪)。也即是说，需要端节点实现各自的跟踪目标，进而利用端节点来辅助中央节点实现中央节点的跟踪。根据这一现实问题的需求，非常有必要研究星型复杂动态网络的中央节点在端节点辅助下的跟踪问题，而目前这方面的研究鲜有报道。

一般情况下，网络不能自发实现既定的跟踪目标，常常需要借助控制手段 [16] 。迄今为止，已经有许多控制用于网络，例如自适应控制 [16] - [21] ，滑模控制 [22] [23] [24] [25] ，牵制控制 [26] [27] ，分散控制 [28] [29] 等。现已有一些文献探讨了复杂动态网络的跟踪控制 [12] [13] [14] [15] [30] [31] [32] 。如：文献 [15] 研究了由链路子系统和节点子系统构成的网络，提出当链路子系统的状态渐近跟踪上设计的辅助跟踪目标时，节点子系统的状态能渐近跟踪上给定的参考目标。文献 [32] 针对由链路子系统和节点系统构成的网络，通过为节点子系统设计控制器，使得链路子系统跟踪上给定的目标，从而使得网络实现了结构平衡。值得指出的是，上述文献为每个节点都施加了控制器，这可能增加控制成本。考虑到降低控制成本以及星型网络的拓扑结构特点，通过仅对中央节点施加控制器实现网络的跟踪便成为非常有研究意义的研究课题。

从现有文献看，有关网络的控制方案几乎都是依赖节点的所有状态分量的信息，例如，文献 [33] 针对具有相同维数节点的星型网络，通过调节端节点与中央节点之间的耦合强度和耦合系数来辅助中央节点在控制的作用下实现中央节点与驱动振荡器的同步。然而在现实网络中，因为数据传输通道拥塞等原因，可能导致节点的部分状态分量信息丢失，即只有节点的部分分量能够用于控制方案的设计。例如，在由机器人群(端节点)协助主刀医生(中央节点)执行手术任务的星型网络中，可能存在个别机器人运动关节受损的情况，此时机器人群仍然能正常协助主刀医生完成手术任务。即中央节点需要在端节点部分状态分量的辅助下实现既定的目标。因此探讨节点部分状态分量用于控制策略的设计具有重要的意义，而目前这方面的研究尚缺乏。

在星型复杂动态网络的研究中，多数网络节点的维数是相同的 [33] [34] [35] [36] 。例如，文献 [35] 针对具有相同维数的耦合时滞星型网络来分析部分振荡死亡(PAD)的稳定性。文献 [36] 针对由四旋翼超混沌系统组成的具有相同维数的反星型网络，研究了一类时间可控的内同步和外同步问题。然而在现实世界中，网络的节点维数可以是不同的，这类网络能表现出更复杂的动态行为。

受上述讨论启发，本文主要研究一类具有不同维数节点的星型复杂动态网络，通过端节点的部分分量辅助中央节点，使得中央节点在控制作用下实现跟踪的问题。与现有关于星型网络跟踪的研究成果相比，本文主要优点如下：(1) 从网络模型上看，本文星型网络的中央节点和端节点和动力学方程各不相同且其状态也可以不相同，这区别于文献 [34] 中的所有节点相同的星型网络。(2) 在控制器的个数上，本文仅为中央节点施加控制，这与文献 [35] 中为所有节点设计控制策略不同，本文的控制策略有希望降低成本。(3) 在端节点的状态信息利用上本文仅利用端节点的部分分量来辅助中央节点来实现跟踪，这与文献 [33] [34] 中利用了端节点的所有状态信息不同。

本文其余部分工作安排如下。第二节给出了网络模型和端节点部分分量选取以及假设工作。第三节设计出自适应控制器和给出了理论证明过程。第四节是数值仿真实例，验证了本文理论结果的有效性，最后给出了研究结论。

符号说明： $R^m$ 表示m维向量集， $R^{n\times m}$ 表示 $n\times m$ 矩阵集， $Z^{+}$ 表示正整数， $X^{\text{T}}$ 表示向量X或矩阵X的转置， $\Vert \cdot \Vert$ 表示向量的欧几里得范数或矩阵的Frobenius范数。

2. 模型描述与准备工作

本文考虑一类含有不同维数节点的星型复杂动态网络，其由1个中央节点(记为节点0)和N个端节点(记为节点 $\text{1},\text{2},\cdots ,N$ )组成，动力学方程如下：

${\stackrel{\dot{}}{x}}_0=f_0\left(x_0\right)+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\delta }_{0i}}{\Gamma }_{0i}{x}_i+u_0$ ， (1a)

${\stackrel{\dot{}}{x}}_i=f_i\left(x_i\right)+{\delta }_{i0}{\Gamma }_{i0}{x}_0,i=1,2,\cdots ,N$ ， (1b)

其中， $x_p={\left(x_{p1},x_{p2},\cdots ,x_{p{n}_p}\right)}^{\text{T}}\in R^{n_p}$ 是节点p ( $p=0,1,\cdots ,N$ )的状态向量， $n_p$ 表示节点p的状态维数。 $f_0\left(x_0\right)\in R^{n_0}$ ， $f_i\left(x_i\right)\in R^{n_i}$ 分别表示节点0和节点i的非线性向量值函数， ${\Gamma }_{0i}\in R^{n_0\times n_i}$ 和 ${\Gamma }_{i0}\in R^{n_i\times n_0}$ 为内耦合矩阵， $u_0\in R^{n_0}$ 为中央节点0的控制输入， ${\delta }_{0i}$ 和 ${\delta }_{i0}$ 分别表示端节点i指向中央节点0以及中央节点0指向端节点i的耦合强度。

不失一般性，本文考虑每个端节点的m ( $m\in Z^{+}$ ， $1\le m\le n_p$ )个状态分量 $x_{i{n}_1},x_{i{n}_2},\cdots ,x_{i{n}_m}$ 来辅助中央节点实现跟踪，其中 $n_m\in Z^{+}$ ， $1\le n_1<n_2<\cdots <n_m\le n_p$ ， $i=1,2,\cdots ,N$ 。

为方便理论分析，引入一个特殊矩阵 $B_p=diag\left(b_1,b_2,\cdots ,b_{n_p}\right)$ ，其中 $b_{n_k}=1\left(k=1,2,\cdots ,m\right)$ ( $m\in Z^{+}$ ， $1\le n_m\le n_p$ )，其余对角元素为0，则

${\tilde{x}}_i=B_i{x}_i$ ， (2)

保留了端节点i的状态分量 $x_{i{n}_1},x_{i{n}_2},\cdots ,x_{i{n}_m}$ 的信息，其它状态分量的信息置为0。

注1. 可以通过一个具体的例子来展示 $B_i$ 的选取。假设一个星型网络的6维端节点i的状态向量为 $x_i={\left(x_{i1},x_{i2},x_{i3},x_{i4},x_{i5},x_{i6}\right)}^{\text{T}}$ ，其需要保留第1，3和6个状态分量，则 $x_{i{n}_1}=x_{i1}\left(n_1=1\right)$ ， $x_{i{n}_2}=x_{i3}\left(n_2=3\right)$ ， $x_{i{n}_3}=x_{i6}\left(n_3=6\right)$ ， ${\tilde{x}}_i={\left(x_{i1},0,x_{i3},0,0,x_{i6}\right)}^{\text{T}}$ ，则特殊矩阵 $B_i=diag\left(1,0,1,0,0,1\right)$ ，使得(2)式成立。容易得知 $B_i^{\text{T}}=B_i$ 。

定义1 考虑星型网络(1)。给出中央节点的跟踪目标 $s_0$ ，如果 $\underset{t\to +\infty }{\text{lim}}\Vert x_0-s_0\Vert =0$ 成立，则称星型网络(1)实现了中央节点的渐近跟踪。

假设星型网络(1)满足以下条件：

假设1：非线性向量值函数 $f_0\left(x_0\right)$ 和 $f_i\left(x_i\right)$ 是已知有界的，外耦合强度 ${\delta }_{0i}$ 和 ${\delta }_{i0}$ 是未知常数。

注2. 星型网络(1)中的节点具有不同维数，这说明本文的网络模型(1)与文献 [33] [34] [35] [36] 的具有相同维数节点的网络模型相比，本文不同维数星型网络跟踪控制能满足更多需求。此外，外耦合强度是未知有界的，这与文 [6] [33] 有所不同。

假设2：对于任意的 $x,y\in R^{n_p}$ ，存在正常数 $\eta \in R$ ，使得星型网络(1)中的函数 $f_p(\cdot )$ 满足

${\left(x-y\right)}^{\text{T}}\left(f_p\left(x\right)-f_p\left(y\right)\right)\le \eta {\left(x-y\right)}^{\text{T}}\left(x-y\right)$ 。 (3)

3. 控制器设计

在这一小节中，设计有效的自适应控制器，以保证星型网络(1)实现定义1意义下中央节点的渐近跟踪。为方便，记 $r_i=x_i-s_i$ 表示端节点的跟踪误差， ${\tilde{r}}_i={\tilde{x}}_i-{\tilde{s}}_i=B_i\left(x_i-s_i\right)$ ( $i=1,2,\cdots ,N$ )表示端节点部分状态分量的跟踪误差， $r_0=x_0-s_0$ 表示中央节点的跟踪误差。

控制目标：为星型网络(1)设计合适控制输入 $u_0$ ，在给定中央节点的跟踪目标 $s_0$ 的情况下，为(1b)中的每个端节点设计辅助跟踪目标 $s_i$ ，且端节点部分分量的辅助跟踪目标为 ${\tilde{s}}_i=B_i{s}_i$ ，使得当 $\underset{t\to +\infty }{\lim }\Vert {\tilde{x}}_i-{\tilde{s}}_i\Vert =\underset{t\to +\infty }{\lim }\Vert B_i\left(x_i-s_i\right)\Vert =0$ 时，网络(1)在控制输入 $u_0$ 的作用下实现中央节点的渐近跟踪，即保证 $\underset{t\to +\infty }{\text{lim}}\Vert x_0-s_0\Vert =0$ 成立。

记模型(1)中 ${\delta }_{0i}$ 和 ${\delta }_{i0}$ 的估计值分别是 ${\hat{\delta }}_{0i}$ 和 ${\hat{\delta }}_{i0}$ ，估计误差分别是 ${\bar{\delta }}_{0i}$ 和 ${\bar{\delta }}_{i0}$ ，且

${\bar{\delta }}_{0i}={\delta }_{0i}-{\hat{\delta }}_{0i}$ ， ${\bar{\delta }}_{i0}={\delta }_{i0}-{\hat{\delta }}_{i0}$ 。 (4)

为实现上述控制目标，根据给定中央节点的跟踪目标 $s_0$ ，设计如下端节点的辅助跟踪目标 $s_i$

${\stackrel{\dot{}}{s}}_i=f_i\left(s_i\right)+{\hat{\delta }}_{i0}{\Gamma }_{i0}{s}_0+d_i{r}_i$ 。 (5)

定理1 考虑星型网络(1)。如果假设1与假设2成立，则网络(1)在控制器

$u_0={\stackrel{\dot{}}{s}}_0-f_0\left(s_0\right)-{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left({\hat{\delta }}_{0i}{\Gamma }_{0i}{x}_i+{\hat{\delta }}_{i0}{\Gamma }_{i0}^{\text{T}}{\tilde{r}}_i\right)}-d_0{r}_0$ ， (6)

和自适应律

${\stackrel{\dot{}}{\hat{\delta }}}_{i0}={\mu }_{i0}{\tilde{r}}_i^{\text{T}}{\Gamma }_{i0}{x}_0$ ， (7)

${\stackrel{\dot{}}{\hat{\delta }}}_{0i}={\mu }_{0i}{r}_0^{\text{T}}{\Gamma }_{0i}{x}_i$ ， (8)

以及动力补偿系统

${\stackrel{\dot{}}{d}}_0=r_0^{\text{T}}{r}_0$ ， (9)

${\stackrel{\dot{}}{d}}_i={\tilde{r}}_i^{\text{T}}{\tilde{r}}_i$ ， (10)

的控制下能实现定义1意义下中央节点的渐近跟踪，其中 ${\mu }_{i0}$ ， ${\mu }_{0i}$ 是可调的正常数。

证明：由星型网络(1)和方程(4)~(6)，可得节点的跟踪误差方程为：

$\begin{array}{c}{\stackrel{\dot{}}{r}}_0={\stackrel{\dot{}}{x}}_0-{\stackrel{\dot{}}{s}}_0=f_0\left(x_0\right)+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\delta }_{0i}}{\Gamma }_{0i}{x}_i+\left({\stackrel{\dot{}}{s}}_0-f_0\left(s_0\right)-{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left({\hat{\delta }}_{0i}{\Gamma }_{0i}{x}_i+{\hat{\delta }}_{i0}{\Gamma }_{0i}^{\text{T}}{\tilde{r}}_i\right)}-d_0{r}_0\right)-{\stackrel{\dot{}}{s}}_0\\ =f_0\left(x_0\right)-f_0\left(s_0\right)+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\delta }_{0i}}{\Gamma }_{0i}{x}_i-{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left({\hat{\delta }}_{0i}{\Gamma }_{0i}{x}_i+{\hat{\delta }}_{i0}{\Gamma }_{i0}^{\text{T}}{\tilde{r}}_i\right)}-d_0{r}_0\\ =f_0\left(x_0\right)-f_0\left(s_0\right)+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{\delta }}_{0i}}{\Gamma }_{0i}{x}_i-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\hat{\delta }}_{i0}}{\Gamma }_{i0}^{\text{T}}{\tilde{r}}_i-d_0{r}_0\end{array}$ 。 (11)

$\begin{array}{c}{\widetilde{\stackrel{\dot{}}{r}}}_i=B_i\left({\stackrel{\dot{}}{x}}_i-{\stackrel{\dot{}}{s}}_i\right)=B_i\left(f_i\left(x_i\right)+{\delta }_{i0}{\Gamma }_{i0}{x}_0-\left(f_i\left(s_i\right)+{\hat{\delta }}_{i0}{\Gamma }_{i0}{s}_0+d_i{r}_i\right)\right)\\ =B_i\left(f_i\left(x_i\right)-f_i\left(s_i\right)\right)+B_i\left({\tilde{\delta }}_{i0}{\Gamma }_{i0}{x}_0+{\hat{\delta }}_{i0}{\Gamma }_{i0}{x}_0-{\hat{\delta }}_{i0}{\Gamma }_{i0}{s}_0-d_i{r}_i\right)\\ ={\tilde{f}}_i\left({\tilde{x}}_i\right)-{\tilde{f}}_i\left({\tilde{s}}_i\right)+B_i{\tilde{\delta }}_{i0}{\Gamma }_{i0}{x}_0+B_i{\hat{\delta }}_{i0}{\Gamma }_{i0}{r}_0-d_i{\tilde{r}}_i\end{array}$ 。 (12)

选取以下Lyapunov候选函数：

$V\left(t\right)=\frac{1}{2}{r}_0^{\text{T}}{r}_0+\frac{1}{2}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}{\tilde{r}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{{\tilde{\delta }}_{0i}^2}{2{\mu }_{0i}}}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{{\tilde{\delta }}_{i0}^2}{2{\mu }_{i0}}}+\frac{{\left(d_0-{\lambda }_0\right)}^2}{2}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\frac{{\left(d_i-{\lambda }_i\right)}^2}{2}}$ ， (13)

其中， ${\lambda }_0$ 和 ${\lambda }_i$ 是可调待定参数。由假设2、方程(11)、方程(12)、自适应律(7)~(10)，可以得到函数 $V\left(t\right)$ 沿着误差系统(11)~(12)的导数为：

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)=r_0^{\text{T}}{\stackrel{\dot{}}{r}}_0+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}{\stackrel{\dot{}}{\tilde{r}}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\mu }_{0i}^{-1}{\tilde{\delta }}_{0i}\left(-{\stackrel{\dot{}}{\hat{\delta }}}_{0i}\right)}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\mu }_{i0}^{-1}{\tilde{\delta }}_{i0}\left(-{\stackrel{\dot{}}{\hat{\delta }}}_{i0}\right)}+\left(d_0-{\lambda }_0\right){\stackrel{\dot{}}{d}}_0+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(d_i-{\lambda }_i\right){\stackrel{\dot{}}{d}}_i}\\ =r_0^{\text{T}}\left(f_0\left(x_0\right)-f_0\left(s_0\right)+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{\delta }}_{0i}}{\Gamma }_{0i}{x}_i-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\hat{\delta }}_{i0}}{\Gamma }_{i0}^T{\tilde{r}}_i-d_0{r}_0\right)\\ +{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}\left({\tilde{f}}_i\left({\tilde{x}}_i\right)-{\tilde{f}}_i\left({\tilde{s}}_i\right)+B_i{\tilde{\delta }}_{i0}{\Gamma }_{i0}{x}_0+B_i{\hat{\delta }}_{i0}{\Gamma }_{i0}{r}_0-d_i{r}_i\right)\\ +{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\mu }_{0i}^{-1}{\tilde{\delta }}_{0i}\left(-{\stackrel{\dot{}}{\hat{\delta }}}_{0i}\right)}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\mu }_{i0}^{-1}{\tilde{\delta }}_{i0}\left(-{\stackrel{\dot{}}{\hat{\delta }}}_{i0}\right)}+\left(d_0-{\lambda }_0\right){\stackrel{\dot{}}{d}}_0+{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(d_i-{\lambda }_i\right)\stackrel{\dot{}}{d}}\end{array}$

$\begin{array}{c}\le \eta r_0^{\text{T}}{r}_0+\eta {\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}{\tilde{r}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{r}_0^{\text{T}}{\tilde{\delta }}_{0i}}{\Gamma }_{0i}{x}_i-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{r}_0^{\text{T}}{\hat{\delta }}_{i0}}{\Gamma }_{i0}^{\text{T}}{\tilde{r}}_i-d_0{r}_0^{\text{T}}{r}_0+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}{B}_i{\tilde{\delta }}_{i0}{\Gamma }_{i0}{x}_0\\ +{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}{B}_i{\hat{\delta }}_{i0}{\Gamma }_{i0}{r}_0-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{d}_i{\tilde{r}}_i^{\text{T}}}{\tilde{r}}_i+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\mu }_{0i}^{-1}{\tilde{\delta }}_{0i}\left(-{\mu }_{0i}{r}_0^{\text{T}}{\Gamma }_{0i}{x}_i\right)}+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\mu }_{i0}^{-1}{\tilde{\delta }}_{i0}\left(-{\mu }_{i0}{\tilde{r}}_i^{\text{T}}{B}_i{\Gamma }_{i0}{x}_0\right)}\\ +d_0{r}_0^{\text{T}}{r}_0-{\lambda }_0{r}_0^{\text{T}}{r}_0+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{d}_i{\tilde{r}}_i^{\text{T}}{\tilde{r}}_i-{\lambda }_i{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}}{\tilde{r}}_i\\ \le \left(\eta -{\lambda }_0\right)r_0^{\text{T}}{r}_0+\left(\eta -{\lambda }_i\right){\displaystyle \underset{i=1}{\overset{N}{\sum }}{\tilde{r}}_i^{\text{T}}}\tilde{r}\end{array}$ (14)

由于 ${\lambda }_0$ 和 ${\lambda }_i,i=1,2,\cdots ,N$ 是可调参数，所以一定存在充分大的 ${\lambda }_p>\eta ,p=0,1,\cdots ,N$ 成立。由(14)式可知 $\stackrel{\dot{}}{V}\left(t\right)\le 0$ ，故 $V\left(t\right)$ 单调递减且 $0\le V\left(t\right)\le V\left(t_0\right)$ 。另外，从(13)式可知， $V\left(t_0\right)$ 是有界的以及(7)~(10)的参数 ${\hat{\delta }}_{i0}$ ， ${\hat{\delta }}_{0i}$ ， $d_0$ 和 $d_i$ 是一致有界的。根据Barbalat’s引理 [37] ，有 $\underset{t\to +\infty }{\text{lim}}{r}_0=O$ 和 $\underset{t\to +\infty }{\lim }{\tilde{r}}_i=O$ 。从而 $\underset{t\to +\infty }{\text{lim}}\Vert r_0\Vert =\underset{t\to +\infty }{\text{lim}}\Vert x_0-s_0\Vert =0$ 和 $\underset{t\to +\infty }{\lim }{\tilde{r}}_i=\underset{t\to +\infty }{\lim }\Vert {\tilde{x}}_i-{\tilde{s}}_i\Vert =0$ ，即意味着当 $\underset{t\to +\infty }{\lim }\Vert {\tilde{x}}_i-{\tilde{s}}_i\Vert =0$ 时，可实现目标 $\underset{t\to +\infty }{\text{lim}}\Vert x_0-s_0\Vert =0$ 。因此，网络(1)实现了定义1意义下中央节点的渐近跟踪。定理1证明完毕。

4. 数值仿真

本节选取一个仿真实例来验证理论结果的有效性。考虑由超混沌Chen系统组成的通信接收基站 [38] 为中央节点(即节点0)和 $N=5$ 个的无人水面艇 [39] 为端节点(即节点i， $i=1,2,3,4,5$ )组成的星型网络，其需要跟踪海上某处信号 $s_0$ ，则网络(1)中

$f_0\left(x_0\right)={\left[a\left(x_{02}-x_{01}\right)+x_{04},d{x}_{01}-x_{01}{x}_{03}+c{x}_{02},x_{01}{x}_{02}-b{x}_{03},x_{02}{x}_{03}+r{x}_{04}\right]}^{\text{T}}$ ， (15)

$f_i\left(x_i\right)={\left[-\frac{d_{11}}{m_{11}}{x}_{i1}+\frac{m_{22}}{m_{11}}{x}_{i2}{x}_{i3},-\frac{d_{33}}{m_{33}}{x}_{i2}+\frac{m_{11}-m_{22}}{m_{33}}{x}_{i1}{x}_{i3},-\frac{d_{22}}{m_{22}}{x}_{i3}+\frac{m_{11}}{m_{22}}{x}_{i1}{x}_{i2}\right]}^{\text{T}}$ ， (16)

其中， $x_{i1}$ 、 $x_{i2}$ 、 $x_{i3}$ 分别表示水面船的前进速度、艏摇角速度、横漂速度。 $a=35$ ， $b=3$ ， $c=12$ ， $d=7$ ， $r=0.6$ ， $m_{11}=0.516\text{kg}$ ， $m_{22}=14.43\text{kg}$ ， $m_{33}=0.516\text{kg}\cdot {\text{m}}^2$ ， $d_{11}=12.18\text{kg}/\text{s}$ ， $d_{22}=207.872\text{kg}/\text{s}$ ， $d_{33}=0.4512\text{kg}\cdot {\text{m}}^2/\text{s}$ 。

不失一般性，网络(1)的矩阵选取如下：

${\Gamma }_{i0}=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1.1+0.01i& 0.01i\end{array}\right)$ ， ${\Gamma }_{0i}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& i+0.5\\ 0& 0& 0.1i\end{array}\right)$ ， (17)

${\delta }_{10}=5$ ， ${\delta }_{20}=8$ ， ${\delta }_{30}=23$ ， ${\delta }_{40}=20$ ， ${\delta }_{50}=15$ ， (18)

${\delta }_{01}=45$ ， ${\delta }_{02}=48$ ， ${\delta }_{03}=42$ ， ${\delta }_{04}=45$ ， ${\delta }_{05}=46$ 。 (19)

中央节点的跟踪目标 $s_0$ 选取为：

$s_0={\left(\begin{array}{cccc}\cos t& 2\sin t& 3\sin t& \sin 2t\end{array}\right)}^{\text{T}}$ 。 (20)

控制方案中的其它参数选取如下：

${\mu }_{01}=0.013$ ， ${\mu }_{02}=0.015$ ， ${\mu }_{03}=0.012$ ， ${\mu }_{04}=0.019$ ， ${\mu }_{05}=0.014$ ， (21)

${\mu }_{10}=55$ ， ${\mu }_{20}=58$ ， ${\mu }_{30}=56$ ， ${\mu }_{40}=61$ ， ${\mu }_{50}=52$ 。 (22)

在下面的仿真中，选取初值 $x_p\left(0\right)\left(p=0,1,2,3,4，5\right)$ ， $s_i\left(0\right)$ ， $i=1,2,3,4,5$ 以及(7)~(10)中的初值 ${\hat{\delta }}_{0i}\left(0\right)$ ， ${\hat{\delta }}_{i0}\left(0\right)$ ， $d_0\left(0\right)$ ， $d_i\left(0\right)$ 如下：

$x_0\left(0\right)=10rand\left(4,1\right)$ ， $x_i\left(0\right)=10rand\left(3,1\right)$ ， $s_i\left(0\right)=10rand\left(3,1\right)$ ，(23)

${\hat{\delta }}_{0i}\left(0\right)=5rand\left(1\right)$ ， ${\hat{\delta }}_{i0}\left(0\right)=5rand\left(1\right)$ ， $d_0\left(0\right)=5rand\left(1\right)$ ， $d_i\left(0\right)=5rand\left(1\right)$ 。(24)

下面运用定理1的跟踪控制方案来实现具有参数(15)~(24)的星型网络端节点部分分量辅助中央节点的跟踪，其跟踪误差如图1所示，其中 $r_{0i}\left(i=1,2,3,4\right)$ 和 ${\tilde{r}}_{kj}\left(k=1,2,3,4,5;j=1,2,3\right)$ 分别表示节点0和节点k部分状态分量的误差分量。

图1表明，运用本文提出的控制策略，具有参数(15)~(24)的星型网络(1)在端节点部分分量辅助下，中央节点的跟踪误差曲线 $r_{0i}$ 能收敛到0，即中央节点 $x_0$ 在端节点部分分量辅助下跟踪上了给定的跟踪信号 $s_0$ 。这充分验证了本文定理1中提出的控制策略是有效的。

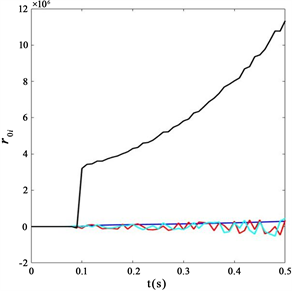
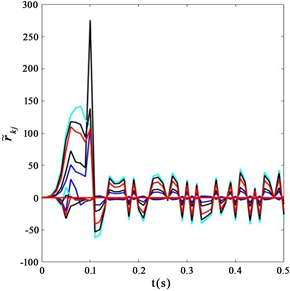(a) 未施加控制器时，中央节点 $x_0$ 的误差响应曲线(b) 未施加控制器时，端节点 $x_i$ 的误差响应曲线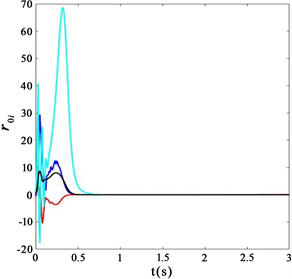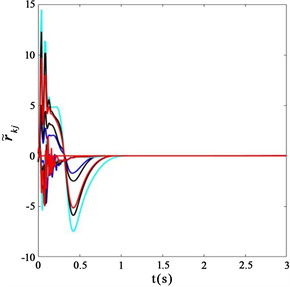(c) 施加控制器后，中央节点 $x_0$ 的跟踪误差响应曲线(d) 施加控制器后，端节点 $x_i$ 的跟踪误差响应曲线

Figure 1. Error response curve of star network (1) with parameters (15)~(24)

图1. 具有参数(15)~(24)的星型网络(1)的误差响应曲线

(7)式、(8)式中的自适应参数的时间响应曲线如图2所示。

图2是本文自适应参数(7)-(8)随时间变化的响应曲线，其验证了未知常数 ${\delta }_{0i}$ 和 ${\delta }_{i0}$ 的估计值是有界的。

5. 结论

本文探讨了一类具有不同维数节点的星型复杂动态网络端节点部分状态分量辅助中央节点实现中央节点跟踪控制问题。针对这类网络，给出了网络中央节点的总体跟踪目标，提出了中央节点的自适应动力补偿跟踪控制方案，利用Lyapunov稳定性理论和Barbalat’s引理，使得中央节点在控制作用下实现跟踪。最后本文通过一个仿真实例验证了所提出控制策略的有效性和可行性。由于实际应用中，可能会受到随机因素的影响。因此，在未来的研究中，将进一步在星型网络模型上考虑随机干扰因素。

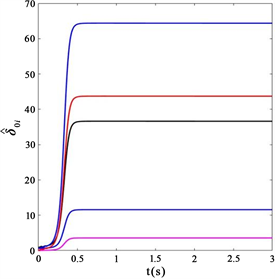
Figure 2. Adaptive time response curves for parameters ${\hat{\delta }}_{0i}$ and ${\hat{\delta }}_{i0}$ ( $i=1,2,3,4,5$ )

图2. 自适应参数 ${\hat{\delta }}_{0i}$ 、 ${\hat{\delta }}_{i0}$ ( $i=1,2,3,4,5$ )的时间响应曲线

基金项目

广东省自然科学基金项目(2020A1515010809)。

NOTES

^*通讯作者。