1. 引言
复变函数是高等院校理、工科普遍开设的一门基础课,也是一些相关研究生入学考试的一门复试课程。复变函数在自然科学和工程技术中有广泛的应用。比如俄国的茹柯夫斯基在设计飞机的时候,就用复变函数论解决了飞机机翼的结构问题。在数学领域的许多分支也都应用了复变函数的理论,它已经深入到微分方程、积分方程、概率论和数论等学科,对它们的发展有着重要影响。
复变函数的课程内容与先修课程高等数学有很多类似的内容,也可以说是在实变函数中的推广和发展。因而我们在教学中采用一个重要的教学方法就是类比法。特别是基础概念,从复变函数的定义、极限、连续、导数乃至积分的定义形式都有密切的联系,但是我们的教学重点应该关注两者之间的不同点。这样才能抓住本质,融会贯通。其中积分部分,高等数学的定积分利用牛顿–莱布尼兹公式,在复平面也有类似的公式,因此计算定积分并不是复变函数课程的重点,计算复围线上的积分才是本课程的重点和难点,也是重要的考点。
是否掌握复围线上的积分也是判断学生是否理解复变函数课程本质的关键点。复变函数的围线积分不仅仅是理论上复的被积函数在封闭曲线上的复积分计算,它还可以用来求解原函数不易求出的定积分和反常积分,比如在研究阻尼振动时遇到的Dirichlet积分;在研究光的折射时的Fresnel积分等。
本文正是基于上述考虑,对复围线上积分进行探索,让学生掌握复围线积分计算,这一个课程核心内容。在文献 [1] 的第三章第7题(7),笔者通过观察学生解答中,发现存在各种普遍的问题。此题非常典型,属于复围线积分的核心类型,非常有必要进行总结分析。本文对此进行了讨论,以帮助读者对复变函数课程核心知识点的理解和掌握。
2. 主要内容
下面我们给出本文的研究对象,一道关于被积函数为有理函数,在圆周上的复积分。通过此题的求解过程,理解和掌握柯西积分定理、柯西积分公式、高阶导数公式,以及留数定理去求解复围线积分。
例:计算沿给定曲线正向的积分:
,
。
为了叙述方便设
。
2.1. 解法一
令
,则
为被积函数
的四个奇点;只有
含于围线C的内部;为了利用柯西积分公式,首先在C内以i为中心作一个正向圆周C1,以−i为中心作一个正向圆周C2 (如图1),C1与C2互不相交,那么被积函数
在由C,C1和C2所围成的区域内是解析的。
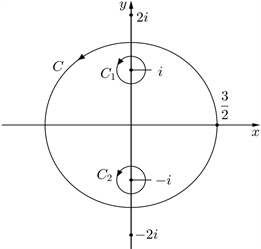
Figure 1. Two singular points within the perimeter
图1. 围线内2个奇点情况
根据复合闭路定理,我们有
易见,函数
和
分别在C1和C2的内部解析,故由柯西积分公式我们有
于是,
注2.1 研究复围线积分的常规思路:先考虑被积函数在围线C内的性质,是否无奇点;如果无,即被积函数在围线C内解析,由柯西积分定理得积分得零;如果有奇点,则分情况考虑内C奇点的个数,若被积函数在C内只有1个奇点,直接利用柯西积分公式可得;若被积函数在C内有几个(多于1个)奇点,就不能直接利用柯西积分公式来计算沿闭曲线C的积分,常需要在C内作几个互不相交的小圆将它们分离,应用复合闭路定理将沿C的积分转化为沿各小圆周的积分之和,再利用柯西积分公式分别计算。此解法为最常规做法。
2.2. 解法二
由于
,故
由于
的两个奇点
在C的外部,故由柯西积分定理得
而
直接由柯西积分公式知
从而
注2.2 此解法首先要观察被积的有理函数简单分解,应用了柯西积分定理及柯西积分公式,形式及计算量简单。避免了使用复合闭路定理,但是要求对有理函数分解直观能力较强的学生。
2.3. 解法三
由于只有两个奇点
含于C的内部,故将被积函数
进行分解为
从而
直接由柯西积分公式可得:
我们有
注2.3 此解法 [2] 首先要深刻认识到被积函数在C的内部只有两个奇点,因而对被积函数的分解具有针对性,只分解分母的一部分,这样分解成两个积分,每个积分只有一个奇点,从而只需要应用柯西积分公式,形式及计算量简单。此方法要求对柯西积分公式及有理函数分解直观能力非常强的学生。
2.4. 解法四
类似解法一,令
,则
为被积函数
的四个奇点;对被积函数逐步降次分解我们有
此时由柯西积分公式知
由柯西积分定理知
我们有
注 2.4 此解法首先要观察到被积的有理函数可逐步降次分解,只应用了柯西积分公式,形式及计算量简单。避免了使用复合闭路定理,需要理解在复数域内:任何有理函数,若分母为零时只有单根,一定可以分解为分母是一次的有理函数之和(可参考文献 [3] )。即
2.5. 解法五
由于被积函数
在C的内部只有两个一级极点
,故
根据留数定理,我们有
注2.5 此解法利用了教材 [1] 中第五章留数的方法,超出第三章知识点范围,此方法本质上也是复合闭路定理的推广,可以总结此法让学生总复习阶段对围线积分进行比较。
2.6. 解法六
MATLAB计算复围线积分,可以利用residue函数求留数命令,但是不容易记忆。实际上,可以参考文献 [4] ,采用最简单的利用参数方程求定积分或者求极限命令即可。
2.6.1. 利用参数方程法
先把围线C化为参数方程
。
MATLAB程序及结果如下:
>> syms z t %定义符号变量
>> z=3/2*cos(t)+3/2*i*sin(t) %定义圆周参数方程
>> f=1/((z^2+1)*(z^2+4)) %定义被积函数f
>> int f=int(f*diff(z),0,2*pi) %调用int函数计算积分
int f = 0
2.6.2. 利用求极限命令
首先理论部分:由于被积函数
在C的内部只有两个一级极点
,其次利用MATLAB计算函数在两点的留数,在MATLAB窗口输入:
>> syms z %定义符号变量
>>f=1/((z^2+1)*(z^2+4)); %定义函数
>>limit(f*(z-i), z, i); %函数在
处留数.
ans=-i/6;
>> limit(f*(z+i), z, -i); %函数在
处留数.
ans=i/6;
即函数在
处的留数为−i/6;在
处的留数为i/6。从而由留数定理得积分为0。
注6:2.6.1方法转化为实积分,其命令与高等数学积分命令一致;2.6.2方法在学习留数理论之后可以发现留数的计算规则之一就是算极限。
3. 推广与总结
在总结上述题目的各类解法之后,我们可以对上述例题进行变形,从而加深学生对例题的理解。比如变式1:当围线C为
。这时问学生所求积分是多少?显然,四个奇点都在围线C外,不用计算,

Figure 2. Four singular points within the perimeter
图2. 围线内4个奇点情况
由柯西积分定理,直接给出答案为0。再给出变式2:当围线C为
。这时问学生所求积分是多少?显然这个时候就困难一些,我们发现在围线C内有四个奇点。可以提出如下问题,上述解法哪些还适用并给出解答?回答:解法一、解法四、解法五、解法六成立,解法二、三不成立。为了方便比较,我们给出其中的解法一、四的解答。相关的复积分的解法,也可以参考文献 [5] [6] [7] 。
3.1. 解法一
令
,则
为被积函数
的四个奇点都在于C的内部;为了利用柯西积分公式,以四个奇点为圆心作互不相交的小圆
,那么被积函数
在由在
和
的所围成的区域内是解析的(如图2)。
根据复合闭路定理,我们有
易见,函数
、
、
和
分别在
和
的内部解析,故由柯西积分公式我们有
类似地有
于是,
3.2. 解法四
令
,则
为被积函数
的四个奇点;对被积函数逐步降次分解,我们有
此时由柯西积分公式知
我们有
基金项目
广东省本科高校教学质量工程建设项目——复变函数课程教学团队(粤教高函〔2020〕19号);2023年度广东省教育科学规划项目——课程思政视域下复变函数课程体系研究与建设(2023GXJK517)。