一个带参数的对偶插值型细分

A Parametric Dual Interpolatory Subdivision

摘要: 对偶插值型细分是近年来提出的一种新型细分格式。它区别于传统的插值型细分格式，不通过逐步插值的方式，而只是确保极限曲线插值于原始控制网格。对偶插值型细分可有效结合了插值型细分和对偶型细分的优势。由于其新颖性，该类格式引起了广泛的学术关注。本文提出了一个带参数的四重九点对偶插值型细分格式，对其连续性和多项式再生性进行了分析，并计算了相应的Hӧlder指数。

Abstract: The dual interpolatory subdivision, a novel subdivision scheme introduced in recent years, dis-tinguishes itself from traditional interpolatory subdivision schemes. Instead of employing a step-wise interpolation approach, it interpolates the limit curve to the original control mesh. This dual interpolatory subdivision effectively amalgamates the advantages of both interpolatory schemes and dual schemes. Owing to its innovative nature, this format has garnered widespread academic interest. This paper presents a parametric quaternary nine-point dual interpolatory subdivision scheme, analyzes its continuity and polynomial reproduction properties, and calculates the cor-responding Hӧlder exponent.

1. 引言

在计算机辅助设计领域，细分方法是一种强大的工具，它通过简单的几何规则和拓扑规则，将粗糙的网格加细连接，获得更精细的控制网格，提供更精细、更复杂的模型。随着计算机技术的进步和图形处理能力的提升，细分方法在计算机图形学、三维建模、动画设计中应用越来越广泛。

根据拓扑规则的不同，细分格式可分为两大类：基本型细分 [1] 和对偶型细分 [2] 。此外，根据细分后生成的极限曲线是否通过初始控制顶点，又可分为逼近型细分和插值型细分。在基本型细分中，k + 1层的控制网格上的顶点除一部分新顶点外，第k层的控制顶点中会通过与周围顶点的线性组合被磨光。相比之下，对偶型细分格式可以视为顶点的分裂过程，第k层的控制顶点消失，产生更多k + 1层控制顶点。典型的插值型细分通常指逐步插值型细分，即第k层的控制顶点在磨光得到k + 1层的控制网格时得以保留下来且保持不变。与之相对的是逼近型细分，其第k层的控制顶点不会保留至k + 1层。因此，传统的插值型细分格式可以看作是逼近型细分。

近年来，一些学者对对偶型细分的极限曲线能否插值控制多边形进行了探讨。2018年，Deng等人 [3] 发现，当n趋近无限时，2重2n点对偶型细分格式的极限曲线可以插值闭合的初始控制网格。2019年，Romani [4] 正式提出了对偶插值型细分的概念，并给出一个构造4重对偶插值型细分的算法。2020年，Romani和Viscardi [5] 详细描述了任意重数曲线对偶插值型细分的特性，并提供了相关构造方法，推动了新型对偶插值型细分格式的发展。2022年，Gemignani等人 [6] 给出了对偶插值型细分需要满足的代数条件，并给出了基于多项式方程求解的构造性算法。2023年，Viscardi [7] 探讨了偶数重和奇数重对偶插值型细分的特点，指出奇数重对偶插值型细分与经典基本型插值型细分之间的关系。目前，关于对偶插值型细分的研究仍相对有限。本文介绍了一种新的四重九点对偶插值型细分格式，该格式具有包含一个可变参数，有较高的灵活性，当参数取定在特定范围内时能达到C³光滑。文献 [6] 中的例2细分格式是此格式的一个特例。当参数取特定值时，该格式可以有更高的Hölder指数。

2. 预备知识

给定初始控制点集 $P^0=\left\{P_j^0\in {ℝ}^d|j\in \mathbb{Z}\right\}$ 通过不断加入新点来构造细分曲线，设 $P^k=\left\{p_j^k\in {ℝ}^d|j\in \mathbb{Z}\right\}$ 为第 $k\left(k\ge 0,k\in \mathbb{Z}\right)$ 次细分后的控制顶点集合，则m重细分格式可表示为

$P_i^{k+1}={\displaystyle \underset{j\in \mathbb{Z}}{\sum }{a}_{i-mj}{P}_j^k},i\in \mathbb{Z},$

其中 $a=\left\{a_i|i\in \mathbb{Z}\right\}$ 称为掩模。插值细分格式的一般形式为

$\{\begin{array}{l}{P}_{mi}^{k+1}=P_i^k,\\ P_{mi+j}^{k+1}={\displaystyle \underset{l\in Z}{\sum }{a}_{mi+j-ml}{P}_l^k},j=1,\cdots ,m-1.\end{array}$

若m重细分格式S一致收敛，则其掩模a满足

${\displaystyle \underset{i\in \mathbb{Z}}{\sum }{a}_{mi+j}}=1,j=0,1,\cdots ,m-1.$ (1.1)

引理2.1 [8] 若m重细分格式S的掩模a满足(1.1)式，则必存在一个细分格式 $S_1$ (称为S的一阶差分格式)，满足

$\text{d}{P}^k=S_1\text{d}{P}^{k-1},$

其中， $P^k=S^k{P}^0$ ， $\text{d}{P}^k=\left\{{\left(\text{d}{p}^k\right)}_i=m^k\left(p_{i+1}^k-p_i^k\right)|i\in \mathbb{Z}\right\}$ 。细分S是一致收敛当且仅当 $\frac{1}{m}{S}_1$ 对任意初始控制网格 $f^0$ 都收敛到零函数。

一般地，将S的n阶差分格式记为 $S_n$ ，其掩模为 $a^{\left(n\right)}={\left\{a_i^{\left(n\right)}\right\}}_{i\in \mathbb{Z}}$ ，则 $S_n$ 的生成多项式为

$a^{\left(n\right)}\left(z\right)={\displaystyle {\sum }_{i\in \mathbb{Z}}{a}_i^{\left(n\right)}{z}^i}={\left(\frac{mz}{1+z+\cdots +z^{m-1}}\right)}^{n}a\left(z\right)$ .

引理2.2 [8] 若m重细分格式S的掩模 $a={\left\{a_i\right\}}_{i\in Z}$ 及差分格式 $S_j\left(j=1,2,\cdots ,n+1\right)$ 存在，且 $\frac{1}{m}{S}_{n+1}$ 对任意初始控制网格 $f^0$ 都收敛到零函数，则m重细分格式S是 $C^n$ 连续的。

为证明细分S是 $C^n$ 连续的，依据引理2.2，只需证明 $n+1$ 阶差分细分 $S_{n+1}$ 存在，并存在一个正整数L满足 ${\Vert {\left(\frac{1}{m}{S}_{n+1}\right)}^L\Vert }_{\infty }<1$ ，其中

${\Vert {\left(\frac{1}{m}{S}_{n+1}\right)}^L\Vert }_{\infty }=\max \left\{{\displaystyle {\sum }_{j\in Z}\left|a_{i+m^{L}j}^{\left[n+1,L\right]}\right|},i=0,1,\cdots ,m^L-1\right\}$ ，

$a^{\left[n+1,L\right]}\left(z\right)={\displaystyle {\sum }_{i,j}{a}_{i+m^{L}j}^{\left[n+1,L\right]}{z}^{i+m^{L}j}}=\frac{1}{m^L}{\displaystyle {\prod }_{j=0}^{L-1}{a}^{\left(n+1\right)}\left(z^{m^j}\right)}$ .

引理2.3 [9] 将数据 $f_i^k\left(i\in \mathbb{Z},k\in {\mathbb{N}}_0\right)$ 与参数值

$t_i^k=t_0^k+\frac{i}{m^k},t_0^k=t_0^{k-1}-\frac{\tau }{m^k}$

相关联，其中 $\tau =\frac{a^{\prime }\left(1\right)}{m}$ 是对应的参数平移。则一个收敛的细分格式 $S_a$ 关于该参数化再生d次多项式当且仅当对 $k=0,\cdots ,d$ ，

$a^{\left(k\right)}\left(1\right)=m\underset{l=0}{\overset{k-1}{{\displaystyle \prod }}}\left(\tau -l\right),a^{\left(k\right)}\left({\zeta }_m^j\right)=0,j=1,\cdots ,m-1,$

其中 ${\zeta }_m^j=\exp \left(\frac{2\pi I}{m}j\right)$ ，I为虚单位。

3. 一种新的四重九点细分格式

下面我们给出四重九点细分格式的加细规则如下

$\{\begin{array}{l}{P}_{4i}^{k+1}=a_{16}{P}_{i-4}^k+a_{12}{P}_{i-3}^k+a_8{P}_{i-2}^k+a_4{P}_{i-1}^k+a_0{P}_i^k+a_{-4}{P}_{i+1}^k+a_{-8}{P}_{i+2}^k+a_{-12}{P}_{i+3}^k+a_{-16}{P}_{i+3}^k,\\ P_{4i+1}^{k+1}=a_{17}{P}_{i-4}^k+a_{13}{P}_{i-3}^k+a_9{P}_{i-2}^k+a_5{P}_{i-1}^k+a_1{P}_i^k+a_{-3}{P}_{i+1}^k+a_{-7}{P}_{i+2}^k+a_{-11}{P}_{i+3}^k+a_{-15}{P}_{i+4}^k,\\ P_{4i+2}^{k+1}=a_{14}{P}_{i-3}^k+a_{10}{P}_{i-2}^k+a_6{P}_{i-1}^k+a_2{P}_i^k+a_{-2}{P}_{i+1}^k+a_{-6}{P}_{i+2}^k+a_{-10}{P}_{i+3}^k+a_{-14}{P}_{i+4}^k,\\ P_{4i+3}^{k+1}=a_{15}{P}_{i-3}^k+a_{11}{P}_{i-2}^k+a_7{P}_{i-1}^k+a_3{P}_i^k+a_{-1}{P}_{i+1}^k+a_{-5}{P}_{i+2}^k+a_{-9}{P}_{i+3}^k+a_{-13}{P}_{i+4}^k,\end{array}$ (3.1)

其中 ${\left\{a_i\right\}}_{i=-16}^{17}$ 为掩模，满足 $a_i=a_{1-i},i=1,2,\cdots ,17$ 。 $a_{-16}$ 到 $a_0$ 依次为

$\begin{array}{l}\frac{\omega }{1024},\frac{25\omega }{3072},-\frac{9381}{315621376}+\frac{25\omega }{512},-\frac{78175}{315621376}-\frac{25\omega }{512},-\frac{30081}{22544384}-\frac{23\omega }{1536},\\ \frac{62025}{22544384}-\frac{89\omega }{1536},\frac{464197}{45088768}-\frac{175\omega }{512},\frac{582183}{45088768}+\frac{175\omega }{512},\frac{76275}{5636096}+\frac{119\omega }{1536},\\ -\frac{131415}{5636096}+\frac{91\omega }{512},-\frac{3727635}{45088768}+\frac{525\omega }{512},-\frac{4620297}{45088768}-\frac{525\omega }{512},-\frac{1628125}{22544384}-\frac{105\omega }{512},\\ \frac{2575125}{22544384}-\frac{469\omega }{1536},\frac{19486893}{45088768}-\frac{875\omega }{512},\frac{32915935}{45088768}+\frac{875\omega }{512},\frac{1361625}{1409024}+\frac{245\omega }{768}.\end{array}$

当 $\omega =\frac{947}{110940}$ 时得到对应的是 [6] 例2格式。

3.1. 光滑性分析

在本节中根据引理2.2给出由细分格式(3.1)生成的极限曲线的收敛性和光滑性的条件并进行证明。

四重九点细分格式(3.1)的生成多项式为

$\begin{array}{c}a\left(z\right)=\frac{z^{-16}}{946864128}{\left(1+z+z^2+z^3\right)}^6\left(1+z\right)(924672\omega +1232896\omega z+\left(-28143+12637184\omega \right)z^2\\ -4\left(9381+59795456\omega \right)z^3+\left(-240873+1061215232\omega \right)z^4+\left(7471320-2526203904\omega \right)z^5\\ +168\left(-167887+23661696\omega \right)z^6+\left(42542808-4571578368\omega \right)z^7\\ +168\left(-167887+23661696\omega \right)z^8+\left(7471320-2526203904\omega \right)z^9\\ +\left(-240873+1061215232\omega \right)z^{10}-4\left(9381+59795456\omega \right)z^{11}\\ +\left(-28143+12637184\omega \right)z^{12}+1232896\omega z^{13}+924672\omega z^{14}).\end{array}$

定理3.1 当参数 $\omega$ 满足 $-\frac{2035}{9632}<\omega <\frac{26181}{240800}$ 时，细分格式(3.1)是C⁰连续的；当 $-\frac{121161}{2033255}<\omega <\frac{110007}{2033255}$ 时，细分格式(3.1)是C¹连续的；当 $\frac{24819}{10479616}<\omega <\frac{23319}{2034158}$ 时，细分格式(3.1)是C²连续的；当 $0.007931<\omega <0.014104$ 时，细分格式(3.1)是C³连续的。

证明：对原函数一阶差分细分序列分组求和得到

$\begin{array}{l}{\Vert \frac{1}{4}{S}_1\Vert }_{\infty }=\max \{\left|\frac{10499243}{39452672}-\frac{2455\omega }{3072}\right|+\left|\frac{16362557}{315621376}-\frac{619\omega }{1024}\right|+\left|\frac{37057}{4931584}-\frac{249\omega }{1024}\right|+\frac{\left|\omega \right|}{1024}\\ +\left|\frac{9381}{315621376}-\frac{125\omega }{3072}\right|+\left|\frac{342959}{315621376}-\frac{107\omega }{3072}\right|+\left|\frac{605\omega }{1024}+\frac{9401489}{315621376}\right|\\ +\frac{5\left|1810816\omega +3671\right|}{39452672},\left|\frac{1071}{131072}-\frac{55\omega }{768}\right|+\left|\frac{20143}{65536}-\frac{55\omega }{768}\right|+\left|\frac{8589}{131072}-\frac{33\omega }{256}\right|+\frac{11}{768}\left|\omega \right|,\\ \left|\frac{25\omega }{128}+\frac{34397}{78905344}\right|+\left|\frac{75\omega }{64}+\frac{189277}{39452672}\right|+\left|\frac{375\omega }{128}+\frac{2745763}{78905344}\right|+\left|\frac{125\omega }{64}+\frac{11063971}{39452672}\right|\}\text{.}\end{array}$

经Mathematica [10] 求解不等式 ${\Vert \frac{1}{4}{S}_1\Vert }_{\infty }<1$ 可得 $-\frac{2035}{9632}<\omega <\frac{26181}{240800}$ 。由引理2.2知此时是C⁰连续的，即是收敛的。

$\begin{array}{l}{\Vert \frac{1}{4}{S}_2\Vert }_{\infty }=\max \{\left|\frac{4598539}{39452672}-\frac{4235\omega }{768}\right|+\left|\frac{1673953}{78905344}-\frac{1061\omega }{384}\right|+\left|\frac{274165}{78905344}-\frac{205\omega }{384}\right|\\ +\left|\frac{425\omega }{768}+\frac{59413}{78905344}\right|+\frac{\left|\omega \right|}{256}+\left|\frac{2095\omega }{768}+\frac{1178113}{78905344}\right|+\left|\frac{1055\omega }{192}+\frac{6857451}{39452672}\right|,\\ \left|\frac{15270491}{39452672}-\frac{305\omega }{192}\right|+\left|\frac{2474309}{39452672}-\frac{375\omega }{256}\right|+\left|\frac{8561873}{78905344}-\frac{235\omega }{256}\right|\\ +\left|\frac{1072783}{78905344}-\frac{89\omega }{128}\right|+\left|\frac{1632443}{78905344}-\frac{33\omega }{128}\right|+\left|\frac{9381}{78905344}-\frac{103\omega }{768}\right|+\frac{19\left|\omega \right|}{768}\}.\end{array}$

经Mathematica求解不等式 ${\Vert \frac{1}{4}{S}_2\Vert }_{\infty }<1$ 可得，由引理2.2知此时是C¹光滑的。

$\begin{array}{l}{\Vert \frac{1}{4}{S}_3\Vert }_{\infty }=\max \{\left|\frac{549}{19264}-\frac{3379\omega }{96}\right|+\left|\frac{6711}{308224}-\frac{419\omega }{48}\right|+\frac{\left|\omega \right|}{32}+\left|\frac{423\omega }{16}+\frac{74983}{308224}\right|,\\ \left|\frac{177327}{308224}-\frac{101\omega }{6}\right|+\left|\frac{171161}{616448}-\frac{23\omega }{2}\right|+\left|\frac{87399}{616448}-\frac{133\omega }{12}\right|+\left|\frac{119163}{1232896}-\frac{37\omega }{12}\right|+\frac{\left|\omega \right|}{12}\\ +\left|\frac{11\omega }{4}+\frac{3127}{1232896}\right|,\left|\frac{9381}{9863168}-\frac{7\omega }{8}\right|+\left|\frac{7\omega }{4}+\frac{1522107}{4931584}\right|+\left|\frac{21\omega }{8}+\frac{569041}{9863168}\right|\}.\end{array}$

经Mathematica求解不等式 ${\Vert \frac{1}{4}{S}_3\Vert }_{\infty }<1$ 的解是 $\frac{24819}{10479616}<\omega <\frac{23319}{2034158}$ ，由引理2.2知此时是C²光滑的。

若要验证该格式具有C³光滑性，需找到正整数L使得 ${\Vert {\left(\frac{1}{4}{S}_4\right)}^L\Vert }_{\infty }<1$ 。经实验发现当 $L=1,2,3,4$ 时均无解。当时， ${\Vert {\left(\frac{1}{4}{S}_4\right)}^5\Vert }_{\infty }<1$ 的范围是 $0.011294<\omega <0.011398$ ；当 $L=6$ 时， ${\Vert {\left(\frac{1}{4}{S}_4\right)}^6\Vert }_{\infty }<1$ 的范围是 $0.008580<\omega <0.013932$ ；当 $L=7$ 时， ${\Vert {\left(\frac{1}{4}{S}_4\right)}^7\Vert }_{\infty }<1$ 的范围是 $0.007931<\omega <0.014104$ 。由引理2.2知此时是C³光滑的。

3.2. 多项式再生性

在本节中根据引理2.3讨论细分格式(3.1)生成多项式的再生性。

定理3.2 四重九点细分格式(3.1)的多项式再生次数是5次。

证明：通过对该细分生成多项式 $a\left(z\right)$ 求一阶导，代入 $z=1$ 得

$a^{\prime }\left(1\right)=2.$

$\tau =\frac{a^{\prime }\left(1\right)}{4}=\frac{1}{2}\text{.}$

计算易得 $a\left(1\right)=4$ ， $\frac{1}{4}{a}^{\prime }\left(1\right)=\tau$ ， $\frac{1}{4}{a}^{″}\left(1\right)=-\frac{1}{4}=\tau \left(\tau -1\right)$ ， $\frac{1}{4}{a}^{‴}\left(1\right)=\frac{3}{8}=\tau \left(\tau -1\right)\left(\tau -2\right)$ ， $\frac{1}{4}{a}^{\left(4\right)}\left(1\right)=-\frac{15}{16}=\tau \left(\tau -1\right)\left(\tau -2\right)\left(\tau -3\right)$ 。 $a^{\left(5\right)}\left(1\right)=\frac{105}{32}=\tau \left(\tau -1\right)\left(\tau -2\right)\left(\tau -3\right)\left(\tau -4\right)$ ，但 $a^{\left(6\right)}\left(1\right)=\frac{229815}{32}\ne -\frac{945}{64}=\tau \left(\tau -1\right)\left(\tau -2\right)\left(\tau -3\right)\left(\tau -4\right)\left(\tau -5\right)$ 且 $a^{\left(k\right)}\left(\exp \left(\frac{2\pi I}{4}j\right)\right)=0$ ， $j=1,2,3$ ， $k=0,1,2,3,4,5$ 。由引理2.3可知细分格式(3.1)的最大多项式再生次数为5次。

3.3. Hӧlder指数

在本节中，我们研究随着 $\omega$ 变化时，细分格式对应极限函数Hӧlder指数的变化规律。计算采用了Matlab程序包ttoolbox工具箱 [11] [12] 。图1展示了当 $\omega$ 在−0.3至0.3变化范围内，细分格式的极限函数的Hӧlder指数变化情况。结果表明，Hӧlder指数先随着 $\omega$ 增加而增大，随后又逐渐减小。图2则详细描绘了Hӧlder指数在极值点附近的变化趋势。图中红色点是文献 [6] 中特例 $\omega =\frac{947}{110940}$ 时的情形，此时Hӧlder指数曲线为3.05087。以0.00025为步长，在−0.005到0.025区间内进行了搜索，发现当 $\omega =0.00675$ 时，Hӧlder指数达到最大值3.0547，大于3.05087。

Figure 1. Hӧlder exponential curve of dual interpolation subdivision scheme (3.1)

图1. 对偶插值细分格式(3.1)的Hӧlder指数曲线

Figure 2. Dual interpolation subdivision scheme (3.1) curve near the maximum value of Hӧlder exponent

图2. 对偶插值细分格式(3.1) Hӧlder指数极大值附近的曲线

3.4. 数值算例

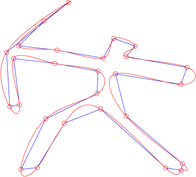
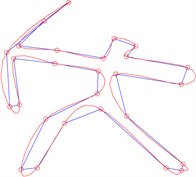
Figure 3. Control polygons of two polylines. The left column is subdivided ( $\omega =0.005$ ) once, and the right column is subdivided ( $\omega =0.005$ ) three times

图3. 两个折线的控制多边形。左列细分( $\omega =0.005$ ) 1次，右列细分( $\omega =0.005$ )三次

图3给出了细分格式(3.1)在 $\omega =0.005$ 时细分一次和三次的效果。左列两幅折线图展示了初始控制网格(以蓝色表示)及其经过一次细分后的结果(以红色表示)。右列的两幅图像则展现了经过三次细分后的控制网格。由于采用了四重细分格式，控制顶点的数量呈现出快速增长的趋势，三次细分后的控制点变得相对密集。此外，观察三次细分后的图像，可以发现原始控制网格在视觉上完全落在极限曲线上。这表明，尽管细分格式(3.1)不是逐步插值型的，但它能够在有限几次加细的情形下就可以达到近似插值的效果。

基金项目

国家自然科学基金(No. 61502217)，辽宁省教育厅科研项目青年项目(LQ2020020)。