Logistic模型分析脑中风影响因素

Logistic Model Was Used to Analyze the Influencing Factors of Cerebral Apoplexy

摘要: 脑中风是一种急性脑血管疾病，是由于脑部血管突然破裂或因血管阻塞导致血液不能流入大脑而引起脑组织损伤的一组疾病。城乡合计脑中风已成为我国第一位死亡原因，也是中国成年人残疾的首要原因。其具有发病率高、死亡率高和致残率高的特点。本文通过对于脑中风数据的描述性分析，建立Logistic回归模型，得到了患脑中风的五个显著的重要因素：年龄、高血压、心脏病、工作类型和平均血糖水平，并得到了经验回归方程。

Abstract: Stroke is an acute cerebrovascular disease, which is a group of diseases caused by the sudden rup-ture of blood vessels in the brain or the blockage of blood vessels that prevents blood from flowing into the brain. Combined urban and rural cerebral apoplexy has become the first cause of death in China and the leading cause of adult disability in China. It has the characteristics of high morbidity, high mortality and high disability rate. In this paper, through descriptive analysis of cerebral stroke data, Logistic regression model was established, and five significant factors of cerebral stroke were obtained: age, hypertension, heart disease, job type and average blood sugar level, and empirical regression equation was obtained.

1. 研究背景

脑中风又称脑卒中，是一种急性脑血管疾病。脑中风是由脑部血管破裂或是血管堵塞导致血液无法流入大脑而引起的一种脑组织损伤疾病，其包括两种：缺血性以及出血性卒中。其中，缺血性卒中的发病比例略高于出血性卒中的发病比例，大概占总发病比例的60%~70%。常见的缺血性卒中多发生在年龄40周岁以上的老年人，颈内动脉和椎动脉闭塞常常是引发老年人缺血性卒中的主要原因。相较于缺血性卒中而言，出血性卒中的危害更加明显，死亡率远高于缺血性卒中。

目前，脑中风已经一跃成为我国致死原因第一位，也是我国成年人残疾的首要原因。对于脑中风的治疗，目前而言预防是最为主要的措施，而高血压是导致脑中风的重要因素之一，因此对于血压的观测应是脑中风患者的重中之重。

关于脑中风的研究，目前国内已有许多学者发表了许多文献研究。刘艳娇 [1] 通过临床流行病学方法研究了肥胖人痰湿体质与脑中风的相关性并证明了肥胖人痰湿体质是引发脑中风的相关因素之一。赵孔华与张沁园 [2] 通过对缺血性脑中风的研究分析出其发病机理以及治疗原则。杜恩 [3] 通过老年脑中风患者观察组与对照组的比较说明了早期康复治疗对于老年脑中风偏瘫患者的重要性。甘勇、杨婷婷以及刘建新等人 [4] 通过对脑中风的研究，分析出了影响脑中风的主要因素。本文选取了该篇文献内的相关指标来使用Logistic回归模型得到几个重要影响因素。

2. 广义线性模型

2.1. 模型介绍

在数据分析的过程中，很多分析方法和模型往往要求目标变量(数据)服从某些假设如正态分布、方差齐次等。一般来说，如果数据不能服从这些假设，那么采用对应的方法或模型获得的结果往往不可信。例如，我们经常使用的经典模型，即形如y = kx + b的一般线性模型就要求数据(目标变量)必须满足正态分布和残差的方差齐次。然而，在实际科研工作中，很多数据往往不能满足以上条件。这种情况就要求我们寻找一种没有以上假设的方法来替代存在假设的模型如：一般线性模型。此时就产生了广义线性模型(GLM)。

在统计学中，广义线性模型(GLM)是普通线性回归的灵活概括，它允许响应变量具有除正态分布以外的误差分布模型。GLM通过允许线性模型通过链接函数与响应变量相关，并允许每种度量的方差大小成为其预测值的函数，从而推广线性回归。广义线性模型由John Nelder和Robert Wedderburn制定，作为统一各种其他统计模型的一种方式，包括线性回归，逻辑回归和泊松回归。他们提出了一种迭代重加权的最小二乘方法，用于模型参数的最大似然估计。最大似然估计仍然很流行，并且是许多统计计算包上的缺省方法。其他方法，包括贝叶斯方法和最小二乘拟合方差稳定响应，已经开发出来。

线性回归模型主要适用于因变量为连续性(特别是服从正态分布)的随机变量的情况，GLM通过一个已知的连接函数将因变量的数学期望与自变量的线性函数连接起来，并将因变量的分布由正态分布推广到广义指数分布族，GLM可以处理因变量为一些离散型、连续性随机变量的回归问题。

在线性回归模型中，设因变量Y与自变量的n组观测值： $\left(Y_i;X_{i1},\cdots ,X_{ip}\right),i=1,\cdots ,n$ ，其有两个基本要素： $Y_1,\cdots ,Y_n$ 相互独立，服从同方差的正态分布 $N\left({\mu }_i,{\sigma }^2\right)$ ； ${\mu }_i=E\left(Y_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}$ ，通常取 $X_{i1}=1,i=1,\cdots ,n$ 。

在广义线性模型中，将 $Y_i$ 的分布由正态分布推广到指数族分布；将 ${\mu }_i$ 推广到它的一个单调、可微函数(称为连接函数) ${\eta }_i=g\left({\mu }_i\right)$ ，使得 ${\eta }_i=g\left({\mu }_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j},i=1,\cdots ,n$ 。

称随机变量 $Y_1,\cdots ,Y_n$ 满足广义线性模型，如果： $Y_1,\cdots ,Y_n$ 相互独立且服从指数族分布；对于某单调、可微的连接函数 $g(·)$ ，有 $g\left({\mu }_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j},i=1,\cdots ,n$ ，其中 ${\mu }_i=E\left(Y_i\right),i=1,\cdots ,n$ 。指数族分布包含诸如二项分布、Poisson分布、正态分布、Γ分布等常见的离散型和连续性分布。对指数族分布的定义为，若Y (一元)概率分布(离散)或概率密度(连续)有如下形式： $f\left(y;\theta ,\varphi \right)=\exp \left(\frac{y\theta -b\left(\theta \right)}{a\left(\varphi \right)}+c\left(y,\varphi \right)\right)$ ，其中 $a(\cdot ),b(\cdot ),c\left(\cdot ,\cdot \right)$ 为已知连续函数， $\theta$ 称为自然参数(表示位置)， $\varphi$ 称为散度参数(表示尺度)，则称Y服从指数族分布。通常， $\theta$ 与 $E\left(Y\right)=\mu$ 有关，是我们所感兴趣的参数， $\varphi$ 与 $Var\left(Y\right)={\sigma }^2$ 有关，通常作为多余参数。

一般连接函数是，连接函数 $g(\cdot )$ 是将自变量第i组观测值的线性组合 ${\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}$ 与 ${\mu }_i=E\left(Y_i\right)$ 联系起来的函数，即 $g\left({\mu }_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j},i=1,\cdots ,n$ 。常见的连接函数有：对数函数， $g\left(\mu \right)=\ln \mu ,\left(\mu >0\right)$ ；Logit或Logistic函数： $g\left(\mu \right)=\ln \left(\mu /\left(1-\mu \right)\right),\left(0<\mu <1\right)$ ；Probit函数或Gauss函数： $g\left(\mu \right)={\Phi }^{-1}\left(\mu \right),\left(0<\mu <1\right)$ ；重对数函数： $g\left(\mu \right)=\ln \left(-\ln \mu \right),\left(0<\mu <1\right)$ ；互补重对数函数： $g\left(\mu \right)=\ln \left(-\ln \left(1-\mu \right)\right),\left(0<\mu <1\right)$ 。

典型连接函数是随机变量Y服从指数族分布，典型连接函数 $g\left(\mu \right)$ 满足 $g\left(E\left(Y\right)\right)=g\left(\mu \right)=\theta$ 。此时， $b^{\prime }\left(\theta \right)=E\left(Y\right)=\mu =g^{-1}\left(\theta \right)$ ， $b^{″}\left(\theta \right)=V\left(\mu \right)=\frac{\text{d}\left(b^{\prime }\left(\theta \right)\right)}{\text{d}\theta }=\frac{\text{d}\left(b^{\prime }\left(\theta \right)\right)}{\text{d}\mu }\frac{\text{d}\mu }{\text{d}\theta }={\left(\frac{\text{d}\theta }{\text{d}\mu }\right)}^{-1}=\frac{1}{g^{\prime }\left(\mu \right)}$ 。

当 $Y~N\left(\mu ,{\sigma }^2\right)$ ： $\theta =\mu$ ，典型连接： $g\left(\mu \right)=\theta =\mu$ ； $Y~P\left(\mu \right)$ ： $\theta =\ln \mu$ ，典型连接： $g\left(\mu \right)=\theta =\ln \mu$ ； $Y~B\left(m,\mu \right)/m$ ： $\theta =\ln \left(\frac{\mu }{1-\mu }\right)$ ，典型连接： $g\left(\mu \right)=\theta =\ln \left(\frac{\mu }{1-\mu }\right)$ ，即Logit (或Logistic)函数； $Y~\Gamma \left(\alpha ,\mu \right)/\alpha$ ： $\theta =1/\mu$ ，典型连接： $g\left(\mu \right)=\theta =1/\mu$ 。

设 $\left(Y_i;X_{i1},\cdots ,X_{ip}\right),i=1,\cdots ,n$ 为因变量Y和自变量 $X_1,\cdots ,X_p$ 的观测值，若： $Y_1,\cdots ,Y_n$ 相互独立，且对每个i， $Y_i$ 服从指数族分布： $Y_i~f\left(y;{\theta }_i,{\varphi }_i\right)=\exp \left(\frac{y{\theta }_i-b\left({\theta }_i\right)}{a\left({\varphi }_i\right)}+c\left(y,{\varphi }_i\right)\right)$ ； $g\left({\mu }_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}$ 其中 ${\mu }_i=E\left(Y_i\right),i=1,\cdots ,n$ ，则称Y与 $X_1,\cdots ,X_p$ 服从广义线性模型(GLM)。

广义线性模型有十分广泛的应用背景，例如：研究人类某种疾病的发病率与人的性别、年龄、家庭经济情况、职业、自然环境情况等的关系，我们可以用典型连接函数创建Logistic模型，通过检验 ${\beta }_j$ 是否显著为0，了解哪些因素是影响该疾病发病率的主要因素，各因素影响发病率的强度等等。还可以研究某地区在某时段内矿难发生次数与矿山类型、企业类型、企业管理水平、企业规模、安全资金投入等等因素的关系，我们可以建立Poisson模型或者对数线性模型来分析。

2.2. GLM的极大似然估计

设有数据： $\left(Y_i;X_{i1},\cdots ,X_{ip}\right),i=1,\cdots ,n$ ， $Y_i$ 服从参数为 ${\theta }_i$ 和 ${\varphi }_i$ 的指数族分布，其概率分布或密度： $f\left(y;{\theta }_i,{\varphi }_i\right)=\exp \left(\frac{y{\theta }_i-b\left({\theta }_i\right)}{a\left({\varphi }_i\right)}+c\left(y,{\varphi }_i\right)\right)$ 。设 ${\mu }_i=E\left(Y_i\right)$ ，选定连接函数 $g(\cdot )$ ，考虑广义线性模型： $g\left({\mu }_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j},i=1,\cdots ,n$ 。

求参数 ${\beta }_1,\cdots ,{\beta }_p$ 的最大似然估计， $Y_1,\cdots ,Y_n$ 的对数似然函数为：

$\ln L\left({\beta }_1,\cdots ,{\beta }_p\right)=\ln \left({\displaystyle \underset{i=1}{\overset{n}{\prod }}f\left(Y_i;{\theta }_i,{\varphi }_i\right)}\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(\frac{Y_i{\theta }_i-b\left({\theta }_i\right)}{a\left({\varphi }_i\right)}+c\left(Y_i,{\varphi }_i\right)\right)}$

由于 ${\theta }_i$ 通过 ${\mu }_i$ 与 ${\beta }_1,\cdots ,{\beta }_p$ 相联系，而 $c\left(Y_i,{\varphi }_i\right)$ 与 ${\beta }_1,\cdots ,{\beta }_p$ 无关，所以 ${\beta }_1,\cdots ,{\beta }_p$ 的最大似然估计即是下列方程组的解：

$\frac{\partial \ln L\left({\beta }_1,\cdots ,{\beta }_p\right)}{\partial {\beta }_r}=\frac{\partial }{\partial {\beta }_r}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(\frac{Y_i{\theta }_i-b\left({\theta }_i\right)}{a\left({\varphi }_i\right)}\right)}=0,r=1,\cdots ,p$

${\mu }_i=b^{\prime }\left({\theta }_i\right)$ ， $V\left({\mu }_i\right)=b^{″}\left({\theta }_i\right)$ ， $g\left({\mu }_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}$ ， ${\mu }_i=g^{-1}\left({\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}\right)$ 。

利用链式求导法则得：

$\frac{\partial {\theta }_i}{\partial {\beta }_r}=\frac{\partial {\theta }_i}{\partial {\mu }_i}\frac{\partial {\mu }_i}{\partial {\beta }_r}={\left(\frac{\partial {\mu }_i}{\partial {\theta }_i}\right)}^{-1}\frac{\partial {\mu }_i}{\partial {\beta }_r}=\frac{1}{b^{″}\left({\theta }_i\right)}\frac{\partial {\mu }_i}{\partial g\left({\mu }_i\right)}\frac{\partial g\left({\mu }_i\right)}{\partial {\beta }_r}=\frac{1}{b^{″}\left({\theta }_i\right)}\frac{1}{g^{\prime }\left({\mu }_i\right)}{X}_{ir}=\frac{X_{ir}}{V\left({\mu }_i\right)g^{\prime }(\; \mu \; i\; )}$

$\frac{\partial b\left({\theta }_i\right)}{\partial {\beta }_r}=\frac{\partial b\left({\theta }_i\right)}{\partial {\theta }_i}\frac{\partial {\theta }_i}{\partial {\beta }_r}=b^{\prime }\left({\theta }_i\right)\frac{\partial {\theta }_i}{\partial {\beta }_r}=\frac{{\mu }_i{X}_{ir}}{V\left({\mu }_i\right)g^{\prime }(\; \mu \; i\; )}$

代入似然方程得 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\left(Y_i-{\mu }_i\right)X_{ir}}{a\left({\varphi }_i\right)V\left({\mu }_i\right)g^{\prime }\left({\mu }_i\right)}}=0$ ，其中 ${\mu }_i=g^{-1}\left({\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}\right)$ 。对很多有重要应用背景的指数族分布，有 $a\left({\varphi }_i\right)=a_i\varphi$ ， $a_i$ 已知。这时似然方程为 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\left(Y_i-{\mu }_i\right)X_{ir}}{a_{i}V\left({\mu }_i\right)g^{\prime }\left({\mu }_i\right)}}=0$ 。

讨论一般情形下的似然方程的迭代最小二乘解。 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\left(Y_i-{\mu }_i\right)X_{ir}}{a\left({\mu }_i\right)V\left({\mu }_i\right)g^{\prime }\left({\mu }_i\right)}}=0$ 。在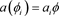的情况下，似然方程为 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\left(Y_i-{\mu }_i\right)X_{ir}}{a_{i}V\left({\mu }_i\right)g^{\prime }\left({\mu }_i\right)}}=0$ 。令 $Z_i=g\left({\mu }_i\right)+\left(Y_i-{\mu }_i\right)g^{\prime }\left({\mu }_i\right)$ ，则 $E\left(Z_i\right)=E\left(g\left({\mu }_i\right)+\left(Y_i-{\mu }_i\right)g^{\prime }\left({\mu }_i\right)\right)=g\left({\mu }_i\right)$ ，由于 $Var\left(Y_i\right)=V\left({\mu }_i\right)a\left({\varphi }_i\right)=a_i\varphi V\left({\mu }_i\right)$ ，因此

$Var\left(Z_i\right)=Var\left(Y_i\right){\left(g^{\prime }\left({\mu }_i\right)\right)}^2=a_i\varphi V\left({\mu }_i\right){\left(g^{\prime }\left({\mu }_i\right)\right)}^2={\tilde{a}}_i\varphi$ 。

从而有：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{Z_i-g\left({\mu }_i\right)}{{\tilde{a}}_i}{X}_{ir}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\left(Y_i-{\mu }_i\right)g^{\prime }\left({\mu }_i\right)}{a_{i}V\left({\mu }_i\right){\left(g^{\prime }\left({\mu }_i\right)\right)}^2}{X}_{ir}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{Y_i-{\mu }_i}{a_{i}V\left({\mu }_i\right)}}\frac{X_{ir}}{g^{\prime }(\; \mu \; i\; )}$

从而似然方程变为 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{Z_i-g\left({\mu }_i\right)}{{\tilde{a}}_i}{X}_{ir}}=0$ ， $E\left(Z_i\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}{\beta }_j}$ 。

若 $Z_i$ 已知，则 ${\beta }_1,\cdots ,{\beta }_p$ 的加权最小二乘估计为 $\hat{\beta }={\left(X^{\text{T}}WX\right)}^{-1}{X}^{\text{T}}WZ$ ，其中， $W=Diag\left(w_1,\cdots ,w_n\right)$ ， $w_i=\frac{1}{{\tilde{a}}_i}=\frac{1}{a_{i}V\left({\mu }_i\right){\left(g^{\prime }\left({\mu }_i\right)\right)}^2}$ ， $Z={\left(Z_1,\cdots ,Z_n\right)}^{\text{T}}$ 。

实际上，Z是未知的，可用迭代加权LS法：

1) 给定 ${\mu }_1,\cdots ,{\mu }_n$ 的一组初值 ${\mu }_1^{\left(0\right)},\cdots ,{\mu }_n^{\left(0\right)}$ ，比如 ${\mu }_i^{\left(0\right)}=Y_i$

2) 计算 $g\left({\mu }_i\right)$ 的初值 ${\eta }_i^{\left(0\right)}=g({\mu }_i^{(\; 0\; )})$

3) 由 $Z_i=g\left({\mu }_i\right)+\left(Y_i-{\mu }_i\right)g^{\prime }\left({\mu }_i\right)$ ，计算 $Z_i$ ， $w_i$ 的初值：

$Z_i^{\left(0\right)}={\eta }_i^{\left(0\right)}+\left(Y_i-{\mu }_i^{\left(0\right)}\right)g^{\prime }\left({\mu }_i^{\left(0\right)}\right)$ ，

$w_i^{\left(0\right)}=\frac{1}{a_{i}V\left({\mu }_i^{\left(0\right)}\right){\left(g^{\prime }\left({\mu }_i^{\left(0\right)}\right)\right)}^2}$ ，

$Z^{\left(0\right)}={\left(Z_1^{\left(0\right)},\cdots ,Z_n^{\left(0\right)}\right)}^{\text{T}}$ ，

$W^{\left(0\right)}=Diag\left(w_1^{\left(0\right)},\cdots ,w_n^{\left(0\right)}\right)$ 。

计算 $\beta ={\left({\beta }_1,\cdots ,{\beta }_p\right)}^{\text{T}}$ 的第一次估计： ${\hat{\beta }}^{\left(1\right)}={\left(X^{\text{T}}{W}^{\left(0\right)}X\right)}^{-1}{X}^{\text{T}}{W}^{\left(0\right)}{Z}^{(\; 0\; )}$

4) 令 ${\eta }^{\left(1\right)}={\left({\eta }_1^{\left(1\right)},\cdots ,{\eta }_n^{\left(1\right)}\right)}^{\text{T}}=X{\hat{\beta }}^{\left(1\right)}$ ，这里 ${\eta }_i^{\left(1\right)}=g\left({\mu }_i^{\left(1\right)}\right)={\displaystyle \underset{j=1}{\overset{p}{\sum }}{X}_{ij}}{\hat{\beta }}_j^{\left(1\right)}$ ， ${\mu }_i^{\left(1\right)}=g^{-1}\left({\eta }_i^{\left(1\right)}\right)$ 。由 ${\mu }_1^{\left(1\right)},\cdots ,{\mu }_n^{\left(1\right)}$ ，根据3)计算得 $Z_i^{\left(1\right)}={\eta }_i^{\left(1\right)}+\left(Y_i-{\mu }_i^{\left(1\right)}\right)g^{\prime }\left({\mu }_i^{\left(1\right)}\right)$ ， $w_i^{\left(1\right)}=\frac{1}{a_{i}V\left({\mu }_i^{\left(1\right)}\right){\left(g^{\prime }\left({\mu }_i^{\left(1\right)}\right)\right)}^2}$ ，由此求得 $\beta$ 的第二次迭代估计：

${\hat{\beta }}^{\left(2\right)}={\left(X^{\text{T}}{W}^{\left(1\right)}X\right)}^{-1}{X}^{\text{T}}{W}^{\left(1\right)}{Z}^{(\; 1\; )}$

5) 重复上述步骤得 $\beta$ 的迭代估计式： ${\hat{\beta }}^{\left(m+1\right)}={\left(X^{\text{T}}{W}^{\left(m\right)}X\right)}^{-1}{X}^{\text{T}}{W}^{\left(m\right)}{Z}^{\left(m\right)}$ ，直到 ${\hat{\beta }}^{\left(m+1\right)}$ 收敛。

3. Logistic模型

3.1. 模型

Logistic模型最早在20世纪四五十年代由Berkson，Dyke和Patterson等人使用过。当因变量Y是0~1变量(二值变量)时，即Y表示分两类的类别，用取值1和0表示，将取值1称为成功，我们关心的时成功的概率 $p=P\left(Y=1\right)$ 。这是一个[0, 1]区间内的值。如果把Y当作一般因变量做线性回归，会给出不合理的结果，比如负值，另外线性回归假定误差项为正态分布在这里也不适用。

如果Y是m次试验中成功的次数，这时可以设Y服从二项分布B(m,p)，关心的是成功概率p，也可以归入相同的模型。

为此考虑对应于二项分布的广义线性回归模型：

$Y~B\left(m,p\right)$ ，

$g\left(p\right)={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k$

其中m为试验次数，Y为m次试验中成功次数，p为给定 $x_1,\cdots ,x_k$ 条件下的成功概率。一般取联系函数 $g\left(p\right)$ 为Logit函数 $\text{logit}\left(p\right)=\ln \left(p/\left(1-p\right)\right)$ 。此模型称为Logistic模型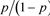，是成功概率与失败概率的比值，称为发生比。 $\ln \left(p/\left(1-p\right)\right)$ 称为对数发生比。

Logistic模型有如下的模型假定：因变量表示成败型结果，为零一变量或者已知试验次数中成功次数；各个观测独立；如果某个观测的试验次数为m，成功概率为p，则因变量方差为mp(1-p)，方差不等于常数值，与期望值mp有关系；对数发生比 $\ln \left(p/\left(1-p\right)\right)$ 与自变量之间为线性关系。

3.2. 最大似然估计

考虑观测的因变量是二值因变量情形。数据为 $\left(x_i,y_i\right)$ ，一个观测对似然函数的贡献为： $p^{y_i}{\left(1-p_i\right)}^{1-y_i}$ ，其中 $p_i={\text{logit}}^{-1}\left(a+b{x}_i\right)=\frac{{\text{e}}^{a+b{x}_i}}{1+{\text{e}}^{a+b{x}_i}}$ ，对数似然函数为：

$\begin{array}{c}l\left(a,b\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left\{y_i\ln p_i+\left(1-y_i\right)\ln \left(1-p_i\right)\right\}}\\ ={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left\{y_i\ln \frac{p_i}{1-p_i}+\ln \left(1-p_i\right)\right\}}\\ ={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left\{y_i\left(a+b{x}_i\right)-\ln \left(1+{\text{e}}^{a+b{x}_i}\right)\right\}}\end{array}$

需要用数值迭代算法求最大似然估计。若样本为满足模型的随机样本，最大似然估计是相合估计，渐近有效估计，具有渐近正态分布。得到最大似然估计 $\left(\hat{a},\hat{b}\right)$ 后，一般用信息阵的逆矩阵估计其协方差阵，信息阵为：

$I\left(a,b\right)=-E\left[\frac{{\partial }^{2}l\left(a,b\right)}{\partial \left(a,b\right)\partial {\left(a,b\right)}^T}\right]$

在用数值迭代算法计算最大似然估计时，一般会得到最大值点处的对数似然函数的海色阵，加上负号并求逆矩阵，就可以作为参数协方差阵估计。有了参数估计的协方差阵估计，就得到了参数估计的标准误差。设参数估计为，估计的方差开平方根作为其抽样分布标准差估计，称为标准误差，记为 $SE\left(\hat{\theta }\right)$ 。令 $Z=\frac{\hat{\theta }}{SE\left(\hat{\theta }\right)}$ ，可以用Z统计量检验 $H_0:\theta =0$ ，在 $H_0$ 成立，大样本且满足适当正则性条件时近似服从标准正态分布。也可用 $Z^2$ 近似服从 ${\chi }^2\left(1\right)$ 分布进行检验。这样对回归系数进行的检验称为Wald类型的检验。此检验对中小样本有一定缺陷，参数的实际数值绝对值较大时，容易错判成不显著。另一种可用的方法是利用偏差统计量的方法。

4. 数据选取、预处理与描述

根据世界卫生组织(WHO)的数据，中风是全球第二大死亡原因，约占总死亡人数的11%。从kaggle上选取脑中风数据集，共有5110条数据，包含id、性别等共12个指标。脑中风数据集包含指标如表1所示。

首先BMI中存在的缺失值删除。将性别指标中的男性改为1，女性改为0，由于只存在一例其他性别，并且女性有2994人，男性有2115人，因此将其设为人数较多女性，这样不至于使误差过大。婚姻状况上，未婚改为0，曾今结过婚改为1。工作类型上，孩子、政府工作、从不工作、私人、自由职业分别对应设置为1~5。居住类型上，城市改为1，农村改为0。在吸烟状况上，曾经吸烟、从不吸烟、吸烟、不明分别对应设置为0~3。

Table 1. Indicator specification

表1. 指标说明

查看处理后数据中的脑中风情况，如图1所示。

Figure 1. Cerebral apoplexy ratio

图1. 脑中风比例

在4909条数据中，脑中风的人数有209人，占比为4.26%。没有脑中风的有4700人，占比为95，74%。在分性别查看患脑中风的情况，如图2所示。

对于选取的2898名女性中，患脑中风的人数为120人，占比为4.14%。选取的男性人数为2011人，患脑中风的人数为89人，占比为4.43%。可以看出，男性、女性患脑中风的比例相差并不是很大，男性要稍微高一点。

再按年龄来看脑中风情况，如图3所示。

我们可以看出，脑中风现象大约是从30岁开始少量出现，并且随着年龄段的增加，脑中风的人数也逐渐增加，50~80岁之间为脑中风的高发年龄段，同时，脑中风率也有增高的趋势。

再按高血压分类来看脑中风情况。如图4所示。

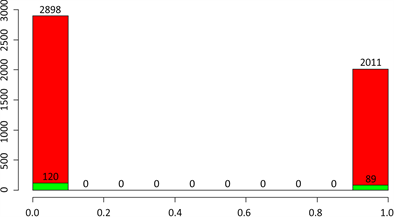
Figure 2. Number of cerebral strokes by sex

图2. 按性别分类脑中风的人数

Figure 3. Cerebral stroke by age

图3. 按年龄分类的脑中风情况

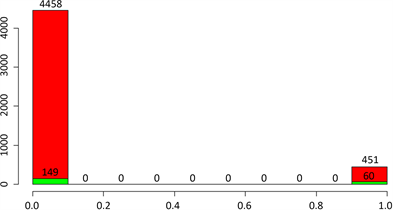
Figure 4. Cerebral stroke classified by hypertension

图4. 按高血压分类的脑中风情况

不患有高血压的4458人中，有149人患了脑中风，比例为3.34%，患有高血压的451人中，有60人患了脑中风，比例为13.3%。可以看出，患有高血压的人群得脑中风的比例比不患高血压的人得脑中风的比例高很多，高了约有10%。

再按心脏病分类来看脑中风情况。如图5所示。

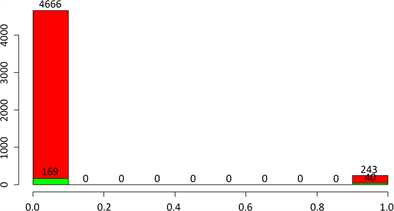
Figure 5. Cerebral stroke classified by heart disease

图5. 按心脏病分类的脑中风情况

不患心脏病的4666人中，有169人患了脑中风，比例为3.62%，患心脏病的243人中，有40人患了脑中风，比例为16.46%。可以看出，患有心脏病的人群得脑中风得比例比不患心脏病的人得脑中风的比例高很多，高了约有13%。

再按结婚状况分类来看脑中风情况。如图6所示。

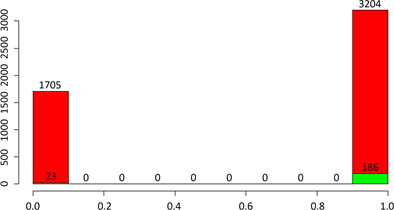
Figure 6. Cerebral stroke classified by marital status

图6. 按结婚情况分类的脑中风情况

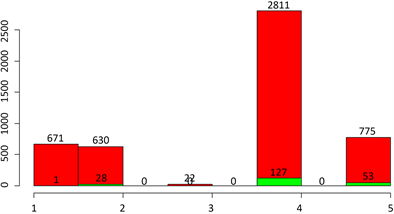
Figure 7. Cerebral stroke classified by type of work

图7. 按工作类型分类的脑中风情况

在未婚的1705人中，只有23人患了闹中风，比例为1.35%，曾经结过婚的3204人中，有186人患了脑中风，比例为5.8%。可以看出，结过婚的人患脑中风的比例要比未婚的人高，这可能主要是和年龄有关，曾经结过婚的人一般年龄较大，而未婚的人年龄较小。

再按工作类型分类来看脑中风情况。如图7所示。

可以看到，各个工作类型的人数分别为671，630，22，2811，775，他们的脑中风情况分别为1，28，0，127，53，比例分别为0.15%，4.44%，0，4.51%，6.84%。可以看到，小孩与从不工作患脑中风的比例最低，几乎为0；自由职业者患脑中风的概率最高，约有7%；政府工作与私人工作的患脑中风的比例相差不大，都约为4.5%。

再按居住地类型分类来看脑中风情况。如图8所示。

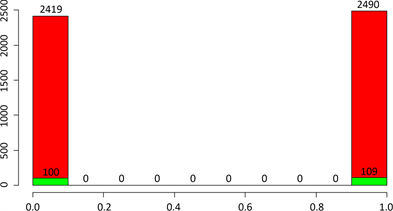
Figure 8. Cerebral stroke classified by type of residence

图8. 按居住地类型分类的脑中风情况

可以看到，居住在城市和农村的人都差不多，得脑中风得人数与比例也都差不多。

再按血糖水平来看脑中风情况。如图9所示。

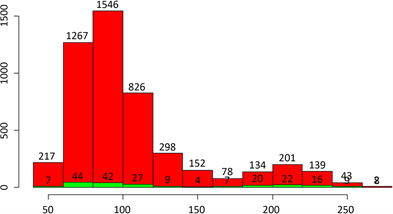
Figure 9. Cerebral stroke classified by blood sugar level

图9. 按血糖水平分类的脑中风情况

可以看到，血糖水平基本都集中在50~150之间，约有4306人，患脑中风的有133人，占比为3.08%，血糖水平150以上约有603人，患脑中风的有74人，占比为12.27%。可以看出，血糖在170~250之间脑中风率较高。

最后是BMI与吸烟情况，对于BMI，各区间患脑中风的比例都约为3%~5%，相差不大。各吸烟情况得脑中风的比例也都相差不大，在6%左右。

5. 模型建立与结果

首先我们通过相关系数查看各自变量之间的线性关系。如图10所示。

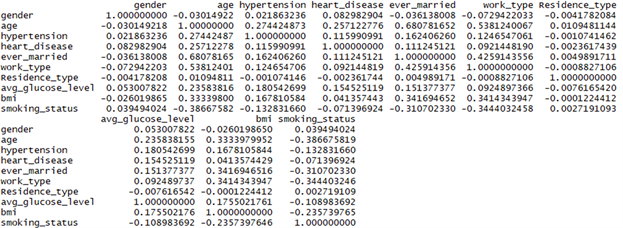
Figure 10. Correlation coefficient of each variable

图10. 各变量相关系数

可以看出，曾经结婚与年龄的相关系数最大，为0.68，还没有达到0.8，不是很强。对于连续型变量来说，年龄越大，血糖的水平较高的人数越多，但总体仍是血糖水平较低的人数多，相关系数为0.23。年龄和BMI之间存在弱相关关系，BMI和血糖水平之间关系不大。再根据之前的描述性统计，工作类型为1、3的为一个水平，2、4的分为一个水平，5为一个水平，所以将它们分为3类。

对其建立广义线性模型中的Logistic回归，结果如图11所示。

Figure 11. Regression result of Logistic

图11. Logistic回归结果

年龄、高血压、心脏病、工作类型和平均血糖水平都通过了显著性检验，与之前的描述性统计相符。在未通过显著性检验的变量中，只有曾经结婚与我们的描述性统计量不符。

由此我们可以得到初步的经验回归方程为：

$\begin{array}{l}\ln \left(\frac{P\left(Y=1\right)}{1-P\left(Y=1\right)}\right)=-7.04+0.004x_1+0.07x_2+0.54x_3+0.39x_4-0.098x_5\\ -0.4x_6+0.02x_7+0.005x_8+0.004x_9-0.03x_{10}\end{array}$

继续进行逐步回归。逐步回归的结果建议我们选取年龄、高血压、心脏病、工作类型和平均血糖水平。对这五个变量和脑中风进行Logistic回归。结果如图12所示。

Figure 12. Regression result of Logistic after selecting the variable

图12. 选择变量后的Logistic回归结果

所有回归系数在0.1的显著性水平下都通过了检验，并且AIC值较之前有所降低。但是心脏病得系数还是不够好，这可能是由于样本中患有心脏病得人比例太少了，仅有243人，而且是两点分布，总人数却有4909人，相较于其他指标，人数是比较少的。我们可以得到经验回归方程：

$\ln \left(\frac{P\left(Y=1\right)}{1-P\left(Y=1\right)}\right)=-7.022+0.07x_2+0.056x_3+0.39x_4-0.39x_6+0.005x_8$

$P\left(Y=1\right)=\frac{\exp \left(-7.022+0.07x_2+0.056x_3+0.39x_4-0.39x_6+0.005x_8\right)}{1+\exp \left(-7.022+0.07x_2+0.056x_3+0.39x_4-0.39x_6+0.005x_8\right)}$

我们可以看出，随着年龄的增加、平均血糖水平的升高，患脑中风的概率也增加，患高血压与心脏病也会增加患脑中风的概率，对于三个水平的工作类型，即孩子、从不工作；私人、政府工作；自由职业，患脑中风的概率也随之降低。

以一个50岁，不患高血压，职业为政府工作，血糖水平为120的人比较其是否患心脏病得脑中风得概率。如果其没有心脏病，则患脑中风得概率为3.5%，反之，患中风得概率为2.4%，有了显著得降低。

6. 结论

年龄、高血压、心脏病、工作类型、平均血糖水平对于判断患脑中风的概率有着显著的影响，年龄是我们不可改变的，工作类型由于生活需要也是不能随意改变的，但是高血压、心脏病、平均血糖水平却可以靠我们自己来改变。在日常生活中多锻炼，多吃一些清淡食物，养成良好的生活习惯，可以有效降低患脑中风的概率。