1. 引言
相位恢复(Phase Retrieval)是数字信号处理中的一个重要的问题,它在图像处理、音频处理以及通信系统等领域中得到广泛应用。传统的数字信号处理中,通常采用快速傅里叶变换(Fast Fourier Transform,FFT)来计算信号的频率和相位信息。但是,FFT算法在大量旋转时很容易出现不同程度的相位失真,因此,在复杂环境下,FFT算法可能会出现错误估计,这种情况会导致恢复的相位精度降低,从而影响到整个系统的性能。
相位恢复问题是从测量的强度信息出发来恢复信号的相位信息,从而达到恢复出已知信号的目的。这一问题长期以来一直是科研工作者的关注热点,已在工程物理领域、天文学观测等方面得到广泛普及。相位恢复问题的经典算法有Gerchberg-Saxton算法(GS算法)、误差减小算法(Error-Reduction Algorithm,ER)、最速下降法(Steepest-Descent Method,SDM)、混合输入输出算法(the Hybrid Input-Output Algorithm,HIO)等 [1] 。
分数阶傅里叶变换(Fractional Fourier transform,简称FRFT)是一种快速傅里叶变换(FFT)的变体,它使用任意复数值来代替傅里叶乘子。这种方法在信号处理、光学和物理学中是很常见的。该算法突破了经典傅里叶变换反映信号的局部特征的能力欠缺的不足之处,在传统的傅里叶变换基础上,通过引入一个实数参数α来泛化的一种傅里叶变换,是对传统傅里叶变换的拓展和推广,因此更适合处理非平稳信号。然而,原有的FRFT算法存在运行效率低下、恢复概率不高等缺陷,因此笔者尝试将GS算法和HIO算法分别与DFRFT算法进行结合,即将这两种算法分别应用于DFRFT算法的预处理阶段。实验表明该方法提高了算法运行速度,提升了算法准确性以及相位恢复的恢复度,是一种满足要求且性能较好的改进算法。
2. 预备知识
2.1. 分数傅里叶变换的定义
分数傅里叶变换的定义形式是多样的,且各个定义形式之间是彼此等价的 [2] 。它是对一般的傅里叶变换的扩展,可以将信号在任意角度进行变换。目前常见的定义形式有以下几种:一方面是由Ozaktas从积分变换给出的采样型FRFT [3] ,另一方面是Namias从傅里叶变换的特征值与特征函数的角度给出的特征分解型FRFT [4] ,这两种定义方式在本质上是彼此等价的。
2.1.1. Ozaktas采样型分数傅里叶变换
对于一维信号
来说,从积分变换的角度给出的FRFT的基本定义为:
其中
(1)
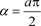 表示信号
在时频平面上旋转的角度,其中a为分数阶次,
称为卷积核,它的形式为:
表示信号
在时频平面上旋转的角度,其中a为分数阶次,
称为卷积核,它的形式为:
(2)
其中,
是狄拉克函数。经验证可知,当
时,
;当
时,
。此定义很容易扩展到
之外的区间,对于虚数单位i来说,
称为恒等算子,也就是说FRFT是周期为4的变换。用符号表示就是:
这一性质在下节介绍分数傅里叶变换性质时也有所涉及。
2.1.2. Namias特征分解型分数傅里叶变换
特征分解型分数傅里叶变换是傅里叶变换的另外一种扩展形式,最早是由Namias于1980年提出,他将一般的傅里叶变换特征值进行了推广,并重新定义了分数傅里叶变换的特征值以及特征函数,后来Lohmann于1993年阐述了FRFT的物理意义,即可理解为时频平面的旋转,Lohmann开创性的工作使得FRFT首先在光学中得到应用。
首先,先给出Hermite-Gaussian函数的傅里叶变换对应的特征方程 [5] :
(3)
其中,
是傅里叶变换算子,
是傅里叶变换的特征值,
称为Hermite-Gaussian函数,即为普通傅里叶变换算子特征值为
的特征函数,且构成有限能量信号空间的一组完备的标准正交基。
1980年,Namias从特征分解的角度将一般的傅里叶变换特征值推广至分数阶次,给出了分数傅里叶变换的特征值与特征函数的形式,从而得到一维信号
的a阶分数傅里叶变换的定义形式:
(4)
或另外一种形式:
(5)
同理,可由一维信号的分数傅里叶变换定义得到二维信号
的FRFT定义 [6] :
(6)
信号
也可以通过二维分数傅里叶逆变换,将
翻转角度
进行恢复:
(7)
2.2. 分数傅里叶变换的性质
分数傅里叶变换的特点是可以在时域和频域之间进行无缝切换,具有更灵活的信号处理能力。同时,它还具备一系列优良性质,如线性性质、阶数性质、周期性、对称性、平移性等。因此,它在信号处理中得到了广泛应用。
(1) 线性性质:
(2) 阶次可加性 [7] :
(3) 周期性:
为整数
(4) 对称性:
(5) 酉性:
式中
表示共轭转置矩阵。
除了上述基本性质之外,分数傅里叶变换与一般的傅里叶变换之间也有某种内在联系。一般的傅里叶变换可以看作信号在时频平面上逆时针旋转
的角度,而分数傅里叶变换可以看成是任意角度的旋转,因此分数傅里叶变换是一般的傅里叶变换的推广形式。
Ozaktas于1994年指出分数傅里叶变换与Wigner-Ville分布(WVD)之间的关系 [8] ,假设信号
的Wigner-Ville分布记为
,则
的Wigner分布是
的Wigner分布的旋转形式:
(8)
若引入Radon变换算子
,那么同样的性质也可以用另外一种形式表达 [9] :
(9)
可理解为
将二维函数
积分投影至与x轴成一角度
的轴上面,将此轴称为
轴或a阶分数傅里叶域。其中,
轴是一般的时域,t轴是一般的频域v [10] 。
3. 数值算法
3.1. DFRFT算法
离散分数傅里叶变换(Discrete Fractional Fourier transform, DFRFT)算法可以通过调节旋转角度来达到不同的变换效果,包括傅里叶变换、傅里叶逆变换、离散傅里叶变换、正弦变换等,因而具有更高的灵活性和适用性。其基本原理是将时域信号通过傅里叶变换转换到频域,然后再对频域信号进行旋转操作,类似于改变信号在时间上的演化速率和方向,最终得到旋转后的信号。
3.2. GS算法
GS算法(Gerchberg-Saxton Algorithm, GS)是一种常见的相位恢复迭代算法,最初是为了解决从两个振幅测量值恢复相位的问题而提出来的。该算法的基本思想是通过迭代来不断调整频谱的相位信息,使得逆变换之后的信号或者图像能够与原始信号或图像的幅度谱尽量接近。这种迭代过程可以逐渐逼近最优解,使得相位信息更加准确。
GS算法的具体流程如下 [11] :
(10)
广义的GS算法可用于任何问题,其中以测量数据或者已知的先验信息形式存在的部分约束在目标域和傅里叶域的振幅是已知的,迭代过程中只需要在两个域之间来回转换,在返回到另一个域之前满足一个域中的约束即可。GS算法的这种推广被称为误差减少算法,顾名思义,可以证明误差在每次迭代时都会减小,此处省略证明。
3.3. HIO算法
混合输入输出算法(Hybrid Input-Output Algorithm)是一种图像重建算法,主要用于恢复被损坏的图像。其算法思想是融合了投影反向模型和后向模型,对目标图像进行逐步修复。
具体而言,该算法主要基于以下两个原理:
(1) 投影反向模型:投影反向模型通过测量得到的图像数据推导出未知目标图像,并用这些数据来矫正模型的误差,从而提高图像恢复的精度。
(2) 后向模型:后向模型通过构造一个假设图像,迭代地更新该图像,直至该图像与观测数据之间达到最佳匹配,进而得到恢复的图像。
混合输入输出算法通过不断迭代,将假设图像与观测数据进行优化匹配,从而实现被损坏图像的重建。该算法可以用于多种领域,如医学图像处理、光学成像等领域。
该算法的具体流程如下 [11] :
(11)
一般的混合输入输出算法就是对于任一随机的初始信号
,在已知该信号频域振幅的情况下对信号进行替换振幅操作进行迭代更新,从而恢复原始信号相位信息的一种方法。其中k指的是迭代次数,
表示对于信号进行傅里叶变换,
是
违背目标域约束的信号分量集合,
为混合输入输出算法的参数,一般取值在
,
为测得的已知信号的频域振幅。然而,HIO算法的前三步和误差减少算法的前三步是一样的,二者的区别仅在于目标域运算。与误差减少算法不同的是,输入
不一定满足目标域约束,它也可以作为下一个输出值
的驱动函数。
时的混合输入输出算法就是误差减少算法。
4. 改进算法流程
4.1. DFRFT_GS算法流程
本节基于离散分数阶傅里叶变换方法和已有的GS方法在相位恢复问题中的应用提出将二者结合用来解决该问题,该方法在本节进行阐述。大量实验证明,这一方法可以通过改变分数阶傅里叶变换的阶数,从而很容易地对原信号进行多次振幅测量,在一定程度上对原来算法的有效性和稳定性加以改进。
基于分数阶傅里叶变换GS算法如算法3.1所示。该算法能够有效提高恢复的唯一性,恢复效果明显优于从时域和频域振幅测量恢复信号的GS算法,并且多次测量也能够确保恢复的唯一性。
4.2. DFRFT_HIO算法流程
本节讨论分数傅里叶变换相位恢复的HIO算法,其算法流程与HIO算法相近。这一算法的主要优势在于可以改变分数阶次进行多次振幅测量,有效提高了信号恢复概率与恢复精度,信号的恢复效果更好,并且可以通过一些数值实验验证这一点。
基于分数阶傅里叶变换的HIO算法如算法4.1所示。该算法在恢复的唯一性上明显优于从时频域振幅恢复信息的HIO算法。但该迭代算法仍有可能收敛至错误信号,也有可能因为无法满足阈值条件导致恢复失败,因此还需要设置最大迭代次数来避免这一情况。
5. 实验仿真与结果分析
5.1. 实验环境
为了验证本文算法的有效性,实验给出了一系列稀疏度不同但是相同长度的信号,并对其分别进行一般的傅里叶变换和分数阶傅里叶变换,观察其恢复概率是否有所提高。
本文生成一些长度n = 64的随机稀疏信号,为获取振幅的准确值,我们采用傅里叶过采样的方法,且振幅长度N = 128。若无特殊说明,实验均是在无噪声的理想环境下进行的。
对于不同稀疏度s的一系列测试信号,我们选取区间
和
作为非零信号值的测试区间进行测试,且设置最大迭代次数为ITER = 6400,定义误差精度
,也就是当近似信号满足条件
时则认为恢复成功。我们设置分数傅里叶变换的分数阶次分别为1.6,1.7和1.8,稀疏度设置区间
,对于其中的每个稀疏度进行100次试验,观察不同的稀疏度的情况下信号的恢复概率情况。
迭代算法的初始信号值随机给定,并且所有的数值实验都是在MATLAB R2022a版本下进行。
5.2. 实验结果对比
为了更一般地讨论算法的优势,本节分别利用以上改进的GS算法和HIO算法通过多个分数域来恢复长度为64的复随机信号,其中信号的实部和虚部都满足
和
上的均匀分布。为了研究利用不同个数的分数阶做相位恢复时恢复概率的问题,我们对于随机信号做了100次重复实验,观察其恢复概率较FFT方法是否有明显提高。
5.2.1. GS算法的恢复效果对比
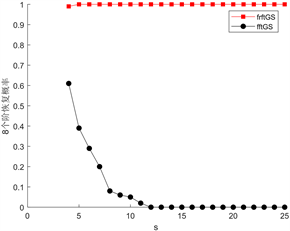
不同个数的分数域数量下两种方法相位恢复概率如图1,其中分数域个数分别为3、4、5、6、7、8。
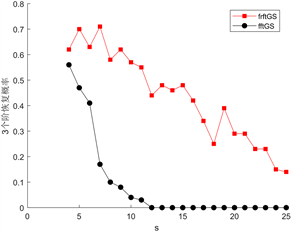
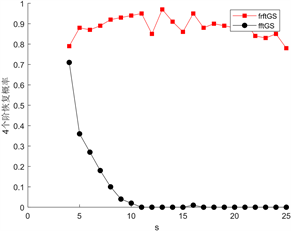
(a) 3个分数域的恢复概率 (b) 4个分数域的恢复概率

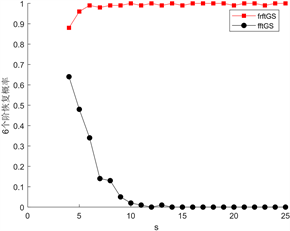 (c) 5个分数域的恢复概率 (d) 6个分数域的恢复概率
(c) 5个分数域的恢复概率 (d) 6个分数域的恢复概率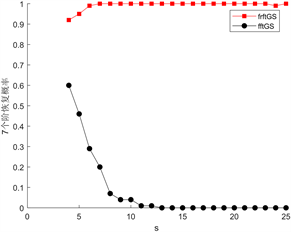
 (e) 7个分数域的恢复概率 (f) 8个分数域的恢复概率
(e) 7个分数域的恢复概率 (f) 8个分数域的恢复概率
Figure 1. Comparison of phase recovery probability between DFRFT_GS method and FFT_GS method under different fractional domains
图1. 不同分数域数量下DFRFT_GS方法与FFT_GS方法相位恢复概率比较
从图中可以看出,分数域个数越多,分数阶傅里叶变换方法的恢复概率越稳定,恢复效果越好。从趋势上面看,一段稀疏信号的稀疏度越低就越难以用一般的傅里叶方法进行恢复,当用到5个或者是更多个数的分数域时,用分数傅里叶变换方法恢复时的概率就趋近于1。总之,恢复效果较一般的傅里叶变换有明显改善。
5.2.2. HIO算法的恢复效果对比
误差精度为
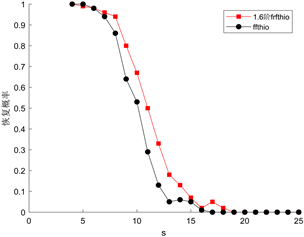
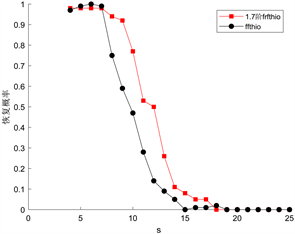
时HIO算法分别结合DFRFT和FFT对于随机信号的恢复结果见图2。当阶数为1.8阶时,分数阶傅里叶变换对于相位恢复问题的处理效果远远比一般的傅里叶变换效果要好。当s = 10时,1.6阶分数傅里叶变换的恢复概率为0.67,1.8阶分数傅里叶变换的恢复概率为0.82,1.7阶分数傅里叶变换的恢复概率为0.77,而傅里叶变换的恢复概率仅为0.53,且当信号越稀疏时本文处理方法的效果越佳,即能更加有效地提高相位恢复概率。当s > 15时两种方法的恢复概率都接近0,也就是说信号越不稀疏则恢复效果就越差,甚至可能恢复失败。
 (a) 1.6阶DFRFT与FFT恢复效果对比 (b) 1.7阶DFRFT与FFT恢复效果对比
(a) 1.6阶DFRFT与FFT恢复效果对比 (b) 1.7阶DFRFT与FFT恢复效果对比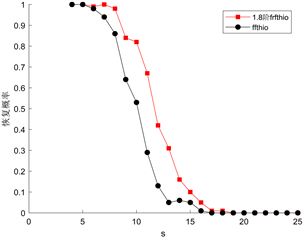 (c) 1.8阶DFRFT与FFT恢复效果对比
(c) 1.8阶DFRFT与FFT恢复效果对比
Figure 2. Comparison of phase recovery probability between DFRFT and FFT with error precision of 0.001
图2. 误差精度为0.001时不同阶数的DFRFT与FFT的相位恢复概率比较
6. 总结
为检验相位恢复效果,本文比较了一般的傅里叶变换以及分数阶傅里叶变换分别与GS算法和HIO算法的叠加算法对稀疏信号的相位恢复结果,发现本文方法处理后的信号较一般的傅里叶变换处理过的信号,其信号的恢复概率显著提高,能够说明本文算法能够在满足恢复精度的情况下有效提高恢复概率。
致谢
在撰写这篇论文期间,我从许多人那里得到了诸多帮助和支持,现在我想向他们表达我的感激之情。
首先,我要感谢我的导师郭兵导师。在整个研究过程中,他给予了我巨大的指导和鼓励。他严谨的学术态度和深厚的知识为我树立了榜样,并在我的研究方向上给予了我全面的指导。无论是在实验设计还是在数据分析过程中,他都给予了我细致入微的指导,并在我的学术道路上给予了无私的帮助。
其次,我还要感谢我的同学和朋友们。他们在我写作过程中提供了许多有益的建议和意见,使我的论文更加准确和完善。感谢我的同门王帅康同学在我论文写作期间给了我莫大的帮助。
此外,我要感谢我的父母和家人。他们一直以来对我的关心和支持使我能够顺利地完成我的学业。他们信任我并鼓励我追求自己的理想,对我来说是无比重要的动力。
最后,我要感谢所有参与这项研究的个人和机构。没有他们的合作和支持,我将无法完成这项研究。他们的贡献和帮助使我能够收集到大量的数据和资料,为我的研究提供了良好的基础。
NOTES
*通讯作者。