物理信息编码解码卷积长短期记忆网络求解时变偏微分方程

Physics-Informed Encoder-Decoder Network Based on ConvLSTM for Solving Time-Dependent Partial Differential Equations

摘要: 本文基于ConvLSTM，构建了一种编码–解码的物理信息深度学习网络框架(PIED-Net)，用于求解含时域的偏微分方程。首先，PIED-Net基于卷积网络提取图像信息中不同层次的空间特征，并使用转置卷积对提取的特征进行表达，实现从图像中学习物理约束的空间信息。为了保证时域信息的连续性，PIED-Net采用ConvLSTM模块，有效地捕捉输入序列的时序关系，提高在预测时间步骤中网络的精度。其次，控制方程、边界和初始条件被用来构建损失函数，并利用有限差分方法来计算各阶导数，进一步提高网络的准确性和稳定性。最后，将所提出的PIED-Net网络框架用来求解2D Burgers方程和2Dflowmixing方程。数值实验结果表明，该网络框架在求解含时域的偏微分方程方面具有出色的精度和运算效率。这为利用深度学习方法解决物理问题提供了一种新的途径。

Abstract: This article presents PIED-Net, a deep learning network framework based on ConvLSTM, for solving time-domain partial differential equations. First, convolutional networks are used to extract spatial features at different levels from image data and transpose convolutions are used to represent these features, enabling the learning of spatial information constrained by physics. ConvLSTM modules are utilized to effectively capture the temporal relationships of neighboring sequences to maintain temporal continuity, and enhance the accuracy of the network in predicting time steps. Besides, governing equations, boundary and initial conditions are employed to construct the loss function, and the finite difference method is employed to calculate derivatives of various orders, further en-hancing the accuracy and stability of the network. Finally, the proposed PIED-Net framework is ap-plied to solve 2D Burgers’ and 2D flow mixing equations, respectively. Numerical experimental re-sults demonstrate that this network framework exhibits outstanding accuracy and computational efficiency in solving time-dependent partial differential equations, presenting a new deep-learning approach for physical problems.

1. 引言

正如Raissi等人 [1] 所述，将神经网络与物理定律相结合，实现物理驱动的偏微分方程求解，这一创新的方法为解决实际工程中复杂问题提供了全新的途径。Zang等人 [2] 利用弱形式将高维线性和非线性偏微分方程转化为算子范数最小化问题，并通过原始和对抗网络的交替更新来逼近最优网络参数，这种方法在解决高维PDE问题时，具有快速、稳定和无网格的特点。Weinan等人 [3] 提出深度Ritz方法，用于数值解决变分问题，该方法具有自然的非线性性和自适应性，并且在高维情况下具有很好的适用性。Sirignano等人 [4] 提出了一种名为深度Galerkin方法(DGM)的算法，通过深度神经网络逼近高维PDE的解，并在无网格的情况下成功解决了自由边界PDE和其他高维PDE问题。Lyu等人 [5] 提出深度混合残差(MIM)算法，将高阶PDE重写为一阶系统，并使用PDE残差作为最小二乘损失函数。Sun [6] 在他的研究中采用深度算子神经网络(DeepONet)，并借鉴PINN的思想，基于物理信息约束提高训练的效率和灵活性。Cao等人 [7] 提出了一种改进的自适应PINN方法，将长时域分解为短时域，并采集不同初始条件下的数值解进行训练，解决了复杂非线性系统的预测和长时间范围稳定预测，并通过构建自适应权重进一步提高预测精度。

然而，这些研究大多基于全连接或其改进的网络结构，没有考虑样本点间的空间关系。因此，研究人员开始关注如何利用卷积网络结构来引入空间信息，从而提高深度学习网络求解偏微分方程的精度和稳定性。Long等人 [8] 提出了一种新型的深度神经网络PDE-Net 2.0，通过结合数值逼近和符号算子，利用观察到的动态数据来发现由偏微分方程控制的隐藏信息，并在建模潜在机制方面提供了灵活性和表达能力。Mo等人 [9] 提出了一种深度卷积编码器–解码器神经网络方法，通过图像到图像的回归策略，有效量化不确定问题，克服了维度灾难挑战。Zhu等人 [10] 提出了一种基于贝叶斯方法的卷积神经网络，通过将基于Stein方法的变分梯度下降算法扩展到深度卷积网络中，实现对数百万个不确定网络参数的近似贝叶斯推断，在论文 [11] 中通过将控制方程纳入损失函数中，实现了在小数据情况下对PDE系统进行代理建模和不确定性量化，同时满足问题约束。Gao等人 [12] 提出了一种新颖的物理约束CNN学习架构，通过引入椭圆坐标映射实现不规则域上参数化PDE问题的解决，相较于全连接神经网络(FC-NN)的PINN，在效率和准确性上表现出明显的优势。Geneva等人 [13] 提出了一种基于物理约束的深度学习方法，通过自回归稠密编码器–解码器卷积神经网络，在计算成本较低的情况下解决和建模非线性动力系统，并实现了对预测量的不确定性量化。

此外，鉴于LSTM处理序列问题时的优异表现，研究人员提出ConvLSTM，通过结合卷积和LSTM (长短期记忆)的特性，能够更高效地建模时空依赖关系。Shi等人 [14] 将降水预测问题转化为一个时空序列预测问题，通过引入卷积结构来扩展全连接LSTM，提出了ConvLSTM模型，证明了ConvLSTM在捕捉时空相关性方面表现更优。Rao等人 [15] 开发了一种名为PeRCNN的新型深度学习架构，通过强制编码已知的物理知识，实现对非线性时空动力系统的数据驱动建模，在数据噪声和稀缺性方面表现出显著的鲁棒性和泛化能力。Ren等人 [16] 提出了一种基于物理信息的卷积循环学习架构，用于低维空间特征提取和时间演化，通过将I/BCs硬编码到网络中来强制满足周期边界填充，将损失函数定义为聚合离散化PDE残差来进行学习。Mavi等人 [17] 提出了一种无监督卷积神经网络架构，采用非局部交互作用解决偏微分方程问题，其中将非局部周期性动态算子固定为卷积核用于导数的计算，提高了其预测能力，具有优越的训练性能和外推能力。

因此，本文提出一种物理信息编码解码卷积长短期记忆网络来求解偏微分方程。该网络采用物理信息约束构建损失函数，降低网络对于样本数量和质量的依赖。此外，在空间上，基于卷积神经网络(CNN)构建编码器和解码器，因此保留了样本点之间的空间信息，能够更精确地捕捉不同层次的物理信息。时间上，采用ConvLSTM更好地刻画时间步进过程中不同时刻的解的相互依赖关系，并且有效防止梯度消失和梯度爆炸，保证网络可以进行长时间预测。

2. 网络架构

首先，本文基于编码/解码技术构建了一个分别包含三个卷积核的编码器和解码器来捕获空间中的场信息，如图1所示。其中：1) 编码器将输入图像转化为低维度的表示，提取出输入图像中的不同层次特征，降低数据的维度和冗余，其采用卷积神经网络Conv2D作为基础，卷积操作使用相同的权重参数对输入的不同位置进行处理，减少了需要学习的参数数量。此外，因其只关注输入中的局部区域，可以捕捉到输入数据的空间局部特征，提高了模型的表达能力；2) 解码器将编码器生成的低维度表示转化为原始数据的高维度表示，其采用转置卷积Conv2DTranspose作为基本结构，实现对数据的还原和重建，使得模型能够生成更高分辨率的输出。

编码器和解码器的计算过程可以表示成：

$u_i^1=\text{Conv2D}\left(u_i\right)$ (1)

$u_i^2=\text{Conv2D}\left(u_i^1\right)$ (2)

$u_i^3=\text{Conv2D}\left(u_i^2\right)$ (3)

$u_{i+1}^1=\sigma \left(\text{Conv2DTranspose}\left(u_i^3\right)+u_i^2\right)$ (4)

$u_{i+1}^2=\sigma \left(\text{Conv2DTranspose}\left(u_{i+1}^1\right)+u_i^1\right)$ (5)

$u_{i+1}=u_{i+1}^3=\sigma \left(\text{Conv2DTranspose}\left(u_{i+1}^2\right)+u_i\right)$ (6)

其中， $u_i^k$ 为输入数据经过k (k = 1, 2, 3)个卷积后的结果， $u_{i+1}^k$ 为数据经过k个转置卷积后的结果，σ为ReLU激活函数。

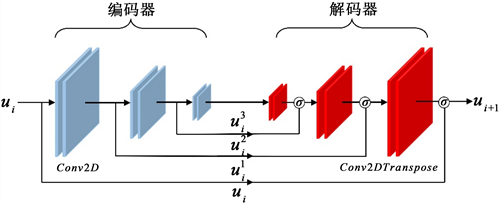
Figure 1. The encoder-decoder network structure

图1. 编码器–解码器网络结构

其次，在上述编码器–解码器结构基础上，在每一个卷积核后增加一个ConvLSTM来捕捉时间序列中相邻时间解的依赖关系，如图2所示。ConvLSTM结合了卷积操作，能够对空间特征进行有效地学习和提取。与传统LSTM相比，ConvLSTM利用卷积操作的参数共享性质，减少了需要学习的参数数量，提高了模型的效率和泛化能力。ConvLSTM的计算公式为：

$i_t=\sigma \left(W_{xi}\ast {\mathcal{X}}_t+W_{hi}\ast {\mathcal{H}}_{t-1}+W_{ci}\circ {\mathcal{C}}_{t-1}+b_i\right)$ (7)

$f_t=\sigma \left(W_{xf}\ast {\mathcal{X}}_t+W_{hf}\ast {\mathcal{H}}_{t-1}+W_{cf}\circ {\mathcal{C}}_{t-1}+b_f\right)$ (8)

${\mathcal{C}}_t=f_t\circ {\mathcal{C}}_{t-1}+i_t\circ \tanh \left(W_{xc}\ast {\mathcal{X}}_t+W_{hc}\ast {\mathcal{H}}_{t-1}+b_c\right)$ (9)

$o_t=\sigma \left(W_{xo}\ast {\mathcal{X}}_t+W_{ho}\ast {\mathcal{H}}_{t-1}+W_{co}\circ {\mathcal{C}}_t+b_o\right)$ (10)

${\mathcal{H}}_t=o_t\circ \tanh \left({\mathcal{C}}_t\right)$ (11)

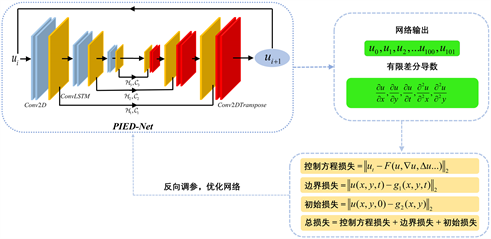
Figure 2. The PIED-Net architecture

图2. .PIED-Net的结构

图2是PIED-Net的网络结构，其中ConvLSTM模块被引入能够更好地预测序列问题，深度捕捉不同时刻下解之间的关系，这种设计保留了底层信息，有助于网络实现长期预测。具体来说，ConvLSTM模块可以有效地捕获时间序列数据中的长期依赖关系，使得模型能够更好地理解时间序列中的动态变化和趋势。最后，利用自回归方法获取一系列预测值，进而计算网络损失并进行反向调参，以提高模型的准确性和稳定性。

3. 基于有限差分的卷积核

由于卷积操作本身是一个非线性运算，且每个神经元只与局部感受域内的神经元相连，无法像全连接神经网络那样在反向传播中直接获得场变量对空间和时间的梯度。因此，利用有限差分方法计算偏微分方程中的场变量对空间和时间的各阶偏导数。在本文中，基于有限差分方法，推导不同阶偏导数的计算公式(12)~(21)及其相对应的卷积核(22)。泰勒展开式的一般形式如下：

$f\left(x\right)=f\left(x_0\right)+f^{\left(1\right)}\left(x_0\right)\left(x-x_0\right)+\frac{f^{\left(2\right)}\left(x_0\right)}{2}{\left(x-x_0\right)}^2+O\left({\left(x-x_0\right)}^2\right)$ (12)

由此可得 $x=x_0+k$ 、 $x_0-k$ 、 $x_0+2k$ 、 $x_0-2k$ 四个点的泰勒展开式：

$f\left(x_0+k\right)=f\left(x_0\right)+f^{\left(1\right)}\left(x_0\right)k+\frac{f^{\left(2\right)}\left(x_0\right)}{2}{k}^2+\frac{f^{\left(3\right)}\left(x_0\right)}{6}{k}^3+\cdots +O\left(k^4\right)$ (13)

$f\left(x_0-k\right)=f\left(x_0\right)-f^{\left(1\right)}\left(x_0\right)k+\frac{f^{\left(2\right)}\left(x_0\right)}{2}{k}^2-\frac{f^{\left(3\right)}\left(x_0\right)}{6}{k}^3+\cdots +O\left(k^4\right)$ (14)

$f\left(x_0+2k\right)=f\left(x_0\right)+f^{\left(1\right)}\left(x_0\right)k+\frac{4f^{\left(2\right)}\left(x_0\right)}{2}{k}^2+\frac{8f^{\left(3\right)}\left(x_0\right)}{6}{k}^3+\cdots +O\left(k^4\right)$ (15)

$f\left(x_0-2k\right)=f\left(x_0\right)-f^{\left(1\right)}\left(x_0\right)k+\frac{4f^{\left(2\right)}\left(x_0\right)}{2}{k}^2-\frac{8f^{\left(3\right)}\left(x_0\right)}{6}{k}^3+\cdots +O\left(k^4\right)$ (16)

将方程(13)与(14)相减，方程(15)与(16)相减可得：

$f\left(x_0+k\right)-f\left(x_0-k\right)=2k{f}^{\left(1\right)}\left(x_0\right)+\frac{f^{\left(3\right)}\left(x_0\right)}{3}{k}^3$ (17)

$f\left(x_0+2k\right)-f\left(x_0-2k\right)=4k{f}^{\left(1\right)}\left(x_0\right)+\frac{8f^{\left(3\right)}\left(x_0\right)}{3}{k}^3$ (18)

因此，得到一阶导数的四阶差分格式为：

$f^{\left(1\right)}\left(x_0\right)=\frac{f\left(x_0-2k\right)-8f\left(x_0-k\right)+8f\left(x_0+k\right)-f\left(x_0+2k\right)}{12k}$ (19)

同理，可得二阶导数的四阶差分格式为：

$f^{\left(2\right)}\left(x_0\right)=\frac{-f\left(x_0-2k\right)+16f\left(x_0-k\right)-30f\left(x_0\right)+16f\left(x_0+k\right)-f\left(x_0+2k\right)}{12k^2}$ (20)

对于时间项，利用中心差分格式来近似其一阶导数：

$f^{\left(1\right)}\left(t\right)=\frac{-f\left(t_0-\Delta t\right)+f\left(t_0+\Delta t\right)}{2\Delta t}$ (21)

由于将控制域划分为均匀网格，因此基于上述差分格式，将卷积网络中卷积核的参数替换为相对应的差分格式，可以得到卷积核的具体公式为：

$\begin{array}{l}\Delta u=\left[\begin{array}{ccccc}0& 0& -\frac{1}{12}& 0& 0\\ 0& 0& \frac{4}{3}& 0& 0\\ -\frac{1}{12}& \frac{4}{3}& -5& \frac{4}{3}& -\frac{1}{12}\\ 0& 0& \frac{4}{3}& 0& 0\\ 0& 0& -\frac{1}{12}& 0& 0\end{array}\right]\times \frac{1}{{\left(\delta h\right)}^2},\frac{\partial u}{\partial x}=\left[\begin{array}{ccccc}0& 0& \frac{1}{12}& 0& 0\\ 0& 0& -\frac{2}{3}& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& \frac{2}{3}& 0& 0\\ 0& 0& -\frac{1}{12}& 0& 0\end{array}\right]\times \frac{1}{\delta h}\\ \frac{\partial u}{\partial y}=\left[\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ \frac{1}{12}& -\frac{2}{3}& 0& \frac{2}{3}& -\frac{1}{12}\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right]\times \frac{1}{\delta h},\frac{\partial u}{\partial t}=\left[\begin{array}{ccc}-\frac{1}{2}& 0& \frac{1}{2}\end{array}\right]\times \frac{1}{\delta t}\end{array}$ (22)

4. 数值实验与结果

4.1. 对比网络

在本节中，将本文提出的网络应用到求解2D Burgers方程和2D flow-mixing方程。为了更好地说明网络的精度和性能，将与Raissi等人 [1] 提出的PINN结果进行对比。在网络参数方面，本文提出的网络(PIED-Net)与对比网络采用完全相同的参数设置，具体为：学习率为10⁻³，以控制网络在训练过程中的权重更新速度；全连接网络层数为[3, 100, 100, 100, 2]，以增强网络的表达能力；采用拉丁超立方采样方法，在问题域和边界上分别选择20,000个点，以确保样本可以涵盖整个问题域；采用正切激活函数以引入非线性因素；使用Adam优化器作为梯度下降优化算法，以确保高效的收敛和训练稳定性。

4.2. 2D Burgers方程

2D Burgers方程在多个学科和领域中都有广泛的应用。在流体力学中，它被用来研究湍流流动、激波形成和传播，以及流体中的非线性行为。在天气和气候模拟中，2D Burgers方程可以用来描述大气运动和气候系统中的非线性现象。

本文对具有Dirichlet边界条件的2D Burgers方程进行了研究，方程定义为：

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{1}{\mathrm{Re}}\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)$ (23)

$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=\frac{1}{\mathrm{Re}}\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)$ (24)

其中，u是流体的平均速度，v是流体的湍流速度，t是时间，x, y是空间的横、纵坐标，Re是雷诺数。该方程的非线性项反映了流体流动中的非线性效应，而扩散项则描述了流体的扩散过程。设置∆t = 0.002 s，Re = 200。

分别利用PINN和PIED-Net求解该问题，向后预测100步，不同时刻的u、v误差分布图绘制在图3中。根据图中的数据，可以清楚地看出本文提出网络预测更精确，绝对误差最大不超过1%，即使在100步时。而与之相比，PINN的误差则分布在整个问题域中。

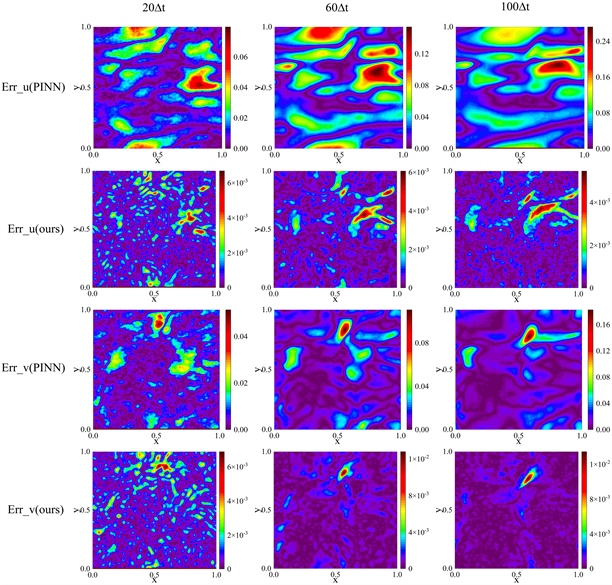
Figure 3. Absolute error plots of predicted and exact solutions for both networks

图3. 两个网络的预测解与精确解的绝对误差图

4.3. 2D Flow Mixing方程

2D flow-mixing方程描述了液体或气体在二维平面上的流动和混合过程，通常用于模拟和分析化工反应器、环境污染扩散、地下水运移等现象。这种方程可以被应用于计算流体力学、化学反应等多个领域，有助于优化工艺设计、预测污染扩散路径以及改善资源利用效率。本节求解一个具有Dirichlet边界条件的2D flow-mixing问题，其问题域为： $x\in \left[\text{1},\text{2}\right]$ ， $y\in \left[\text{1},\text{2}\right]$ ， $t\in \left[0,0.\text{2}\right]$ 。该问题的控制方程定义为：

$\frac{\partial u}{\partial t}+a\frac{\partial u}{\partial x}+b\frac{\partial u}{\partial y}=0$ (25)

其中，系数a、b的计算公式描述为：

$a\left(x,y\right)=-\frac{v_t}{v_{t\max }}\frac{y}{r}$ (26)

$b\left(x,y\right)=\frac{v_t}{v_{t\max }}\frac{x}{r}$ (27)

$v_t={\mathrm{sech}}^2\left(r\right)\tanh \left(r\right)$ (28)

$r=\sqrt{x^2+y^2}$ (29)

式中 $v_t{}_{\max }=0.385$ 。

PIED-Net的预测解与真实解的绝对误差绘制在图4中，同时，对比网络PINN的结果也在图中列出。可以看出，本文提出的网络预测性能要优于对比网络，其误差比对比网络低1个数量级。对比结果表明本网络在对2Dflow-mixing方程进行求解时能够给出更精确的解，网络的预测性能更为优秀。

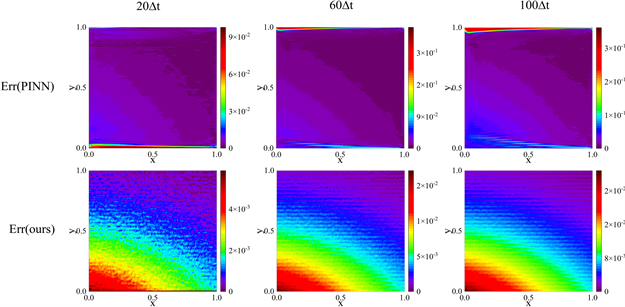
Figure 4. Absolute error plots of predicted and exact solutions for both networks

图4. 两个网络的预测解与精确解的绝对误差图

5. 结论

本论文基于编码–解码结构和ConvLSTM构建一个深度学习物理驱动模型，用于预测带时域的偏微分方程的动态演变。其中，编码–解码结构的作用是将输入数据转化为潜在表示，以提取关键特征并去除冗余信息，同时通过逆向操作将编码后的潜在表示解码为原始输入的重建或生成结果。进一步地，引入了ConvLSTM模块，使得网络可以学习到时间序列数据中的时序依赖关系，并能够捕捉到长期的时间依赖关系。此外，通过使用有限差分卷积核来处理导数项，这种处理方式能够更好地捕捉到数据中的导数信息，从而进一步提高了模型的准确性和泛化能力。通过以上的设计和结构，本文所提出的深度学习物理驱动模型能够有效地预测时变偏微分方程的动态演变，从而为物理建模和预测提供了一种新的方法。

基金项目

山西省青年科学研究基金项目(No. 20210302124159)；国家自然科学基金项目(No. 12102283)。

NOTES

^*通讯作者。