广义Petersen图的混合边邻域粘连度

doi:10.12677/AAM.2024.132070

期刊菜单

广义Petersen图的混合边邻域粘连度
The Mixed Edge Neighbor Tenacity of Generalized Petersen Graphs

DOI: 10.12677/AAM.2024.132070, PDF, HTML, XML, 下载: 40 浏览: 59
作者: 段云清, 武彩萍^*：太原理工大学数学学院，山西晋中
关键词: 广义Petersen图；网络抗毁性；混合边邻域粘连度；Generalized Petersen Graph； Network Invulnerability； Mixed Edge Neighbor Tenacity

摘要: 已知图的混合边邻域粘连度概念以及几类基本图的参数计算公式后，本文给出了广义Petersen图的混合边邻域粘连度的计算公式，使得混合边邻域粘连度算法更为细化，刻画某些网络的抗毁性更为精确。

Abstract: After the concept of mixed edge neighbor tenacity of graphs and the formula for calculating param-eters of some basic graphs are known, the formula for calculating mixed edge neighbor tenacity of generalized Petersen graph is given, which makes the algorithm of mixed edge neighborhood adhe-sion more refined and the damage resistance of some networks more accurate.

文章引用：段云清, 武彩萍. 广义Petersen图的混合边邻域粘连度[J]. 应用数学进展, 2024, 13(2): 723-729. https://doi.org/10.12677/AAM.2024.132070

1. 引言

网络已在当今社会广泛普及，网络抗毁性起源于计算机网络，是通信网络连通性研究的一个重要概念。1985年Gunther和Hartnell提出了间谍网络的概念 [1] ，他们通过一个图来模拟间谍网络，其中图的顶点代表间谍或站点，边代表通讯方式。间谍网络最重要的特性是：如果间谍被捕，与他们直接接触的间谍是不可靠的。2006年，南海地震的发生导致部分国际海底通讯电缆中断，使得许多国家和地区通信故障，某些地区的互联网接入和语音通话也受到影响。基于上述背景的抗毁性参数，称为邻域抗毁性参数。

在网络抗毁性分析中，主要考虑三个因素 [2] ：1) 破坏网络的难易程度；2) 网络被破坏的严重程度；3) 有多少顶点仍然保持连通。因此，邻域连通度 [1] [3] 、边邻域连通度 [4] [5] 、邻域完整度 [6] 、边邻域完整度 [7] 、邻域离散数 [8] 、边邻域离散数 [9] [10] 、邻域坚韧度 [11] 、边邻域坚韧度 [12] [13] 、邻域毁裂度 [14] 、边邻域毁裂度 [15] [16] 等参数被引入，以衡量网络在“邻域”情形下的抗毁性。

设 $G = (V, E)$ 是一个简单图，分别称 $N (e) = {f | f \in E (G), 且 e 和 f 相邻}$ 和 $N [e] = N (e) \cup {e}$ 为e的开邻域和闭邻域。若 $X \subseteq E (G)$ ，则分别称 $N (X) = {f | X \in E (G), f \in E / X 且存在 e \in X, 使得 e 和 f 相邻}$ 和 $N [X] = N (X) \cup {X}$ 为X的开邻域和闭邻域。若将 $N [X]$ 中的边和与X中的边关联的点均从中G删除，则称X为G的一个边颠覆策略，记剩余子图为 $G / X$ 。对连通图G，设 $X \subseteq E (G)$ ，若 $G / X$ 不连通，或孤立点或空集 $\emptyset$ ，则称X为G的一个邻域边割集。

定义1 [1] 设G是连通图，其边邻域连通度的定义为： $Λ (G) = \min {| X | : X \subseteq E (G)}$ ，其中X为G的邻域边割集。

边邻域连通度是基于(1)考虑的。

定义2 [7] 设G是连通图，其边邻域完整度的定义为： $E N I (G) = \min {| X | + m (G / X) : X \subseteq E (G)}$ ，其中 $m (G / X)$ 为 $G / X$ 的最大连通分支的阶。

边邻域完整度是基于(1)和(3)考虑的。

定义3 [9] 设G是连通图，其边邻域离散数的定义为： $E N S (G) = \min {ω (G / X) - | X | : X \subseteq E (G)}$ ，其中X为G的邻域边割集， $ω (G / X)$ 为 $G - X$ 的连通分支数。

定义4 [12] 设G是连通图，其边邻域坚韧度的定义为： $t_{E N} (G) = \min {\frac{| X |}{ω (G / X)} : X \subseteq E (G)}$ ，其中X为G的邻域边割集， $ω (G / X)$ 为 $G - X$ 的连通分支数。

边邻域离散数和边邻域坚韧度是基于(1)和(2)考虑的。边邻域坚韧度是边邻域离散数的除法形式，尽管这两个参数在定义上有一些相似之处，但在衡量网络的抗毁性方面作用不同。

定义5 [15] 设G是连通图，其边邻域毁裂度的定义为： $E N R (G) = \min {ω (G / X) - | X | - m (G / X) : X \subseteq E (G)}$ ，其中X为G的邻域边割集， $m (G / X)$ 和 $ω (G / X)$ 为 $G / X$ 的最大连通分支的阶和连通分支数。

边邻域毁裂度是基于(1)、(2)和(3)考虑的，是视角较为全面的抗毁性参数。

为了更好地刻画边失效情形下的网络抗毁性，闫伟等人提出图的混合边邻域粘连度的概念。

定义6 [17] 设G是连通图，其混合边邻域粘连度定义为 $M E N T (G) = \min {\frac{| X | + m (G / X)}{ω (G / X)} : X \subseteq E (G)}$ ，其中X为G的邻域边割集， $m (G / X)$ 和 $ω (G / X)$ 为 $G / X$ 的最大连通分支的阶和连通分支数。若有 $X^{*}$ ，使得 $M E N T (G) = \min {\frac{| X^{*} | + m (G / X^{*})}{ω (G / X^{*})}}$ ，则称 $X^{*}$ 为G的一个混合边邻域粘连集，简记为MENT-集。显然，混合边邻域粘连度越大，网络抗毁性越好。

混合边邻域粘连度和边邻域毁裂度在衡量网络的抗毁性方面作用不同。目前已经研究了 $P_{n} (n \geq 3)$ 、 $C_{n} (n \geq 3)$ 、 $T_{n, k} (2 \leq k \leq n - 3)$ 、 $S_{1, n - 1} (n \geq 4)$ 、 $D S (m, n)$ 、 $K_{n} (n \geq 3)$ 、 $K_{m, n}$ 、 $K_{n 1, n 2, \dots, n p}$ 等(当p比较大时，完全p部分图的最大匹配需通过算法解决 [18] )基本图的混合边邻域粘连度计算公式，下文我们将研究广义Petersen图的混合边邻域粘连度计算公式。

本文所讨论的图均是简单无向图，未定义的概念和术语参见文献 [19] [20] 。

2. 广义Petersen图的混合边邻域粘连度

考虑广义Petersen图的混合边邻域坚韧度，先了解其定义及其部分性质，具体如下：

定义2.1

对于正整数n和t满足 $n \geq 3$ ， $1 \leq t \leq n - 1$ ，且 $2 t \neq n$ ，定义广义Petersen图 $P (n, t)$ 为： $V (P (n, t)) = {u_{1}, u_{2} ， \dots, u_{n}; v_{1}, v_{2}, \dots, v_{n}}$ ， $E (P (n, t)) = {(u_{i}, u_{i + 1}), (u_{i}, v_{i}), (v_{i}, v_{i + t})}$ ，其中下标关于模n同余。

Watkins等人证明了 $P (n, t)$ 与 $P (n, n - t)$ 同构。图1所示为广义Petersen图 $P (5, 2)$ ，由于该图在各种图论文献中经常出现，人们习惯上称之为Petersen图。

Figure 1. Petersen graph

图1. Petersen图

定理2.2

对广义Petersen图 $P (n, 1)$ 有 $M E N T (P (n, 1)) = {\begin{cases} \frac{4 k + 1}{4 k}, n = 6 k, k \neq 0 \\ \frac{2 k + 1}{2 k}, n = 6 k + 1, k \neq 0 \\ \frac{4 k + 3}{4 k + 1}, n = 6 k + 2, k \neq 0 \\ \frac{4 k + 3}{4 k + 2}, n = 6 k + 3 \\ \frac{2 k + 2}{2 k + 1}, n = 6 k + 4 \\ \frac{4 k + 5}{4 k + 3}, n = 6 k + 5 \end{cases}$ ，其中 $k \in Z^{+}$ 。

证明显然 $M E N T (P (3, 1)) = \frac{3}{2}$ ， $M E N T (P (4, 1)) = 2$ ， $M E N T (P (5, 1)) = \frac{5}{3}$ 。根据n被6除的余数，分以下六种情形讨论(其中 $k \in Z^{+}$ )。

情形1 $n = 6 k, k \neq 0$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}} \cup {v_{2} v_{3}, v_{5} v_{6}, \dots, v_{6 k - 1} v_{6 k}}$ ，结合图 $P (6 k, 1)$ 结构(如图2所示)可知，X为 $P (6 k, 1)$ 的一个MENT-集，容易知道 $| X | = 4 k$ ， $m (P (6 k, 1) / X) = 1$ 且 $ω (P (6 k, 1) / X) = 4 k$ ，则 $M E N T (P (6 k, 1)) = \frac{4 k + 1}{4 k}$ 。

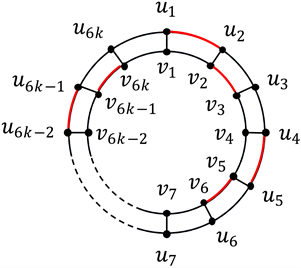
Figure 2. P(6k, 1) and a MENT-set of P(6k, 1)

图2. P(6k, 1)及其一个MENT-集

情形2 $n = 6 k + 1, k \neq 0$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}} \cup {v_{2} v_{3}, v_{5} v_{6}, \dots, v_{6 k - 1} v_{6 k}} \cup {u_{6 k + 1} v_{6 k + 1}}$ ，结合图 $P (6 k + 1, 1)$ 结构可知，X为 $P (6 k + 1, 1)$ 的一个MENT-集，容易知道 $| X | = 4 k + 1$ ， $m (P (6 k + 1, 1) / X) = 1$ 且 $ω (P (6 k + 1, 1) / X) = 4 k$ ，则 $M E N T (P (6 k + 1, 1)) = \frac{2 k + 1}{2 k}$ 。

情形3 $n = 6 k + 2, k \neq 0$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}, u_{6 k + 1} u_{6 k + 2}} \cup {v_{2} v_{3}, v_{5} v_{6}, \dots, v_{6 k - 1} v_{6 k}} \cup {u_{6 k + 2} v_{6 k + 2}}$ ，结合图 $P (6 k + 2, 1)$ 结构可知，X为 $P (6 k + 2, 1)$ 的一个MENT-集，容易知道 $| X | = 4 k + 2$ ， $m (P (6 k + 2, 1) / X) = 1$ 且 $ω (P (6 k + 2, 1) / X) = 4 k + 1$ ，则 $M E N T (P (6 k + 2, 1)) = \frac{4 k + 3}{4 k + 1}$ 。

情形4 $n = 6 k + 3$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}, u_{6 k + 1} u_{6 k + 2}} \cup {v_{2} v_{3}, v_{5} v_{6}, \dots, v_{6 k + 2} v_{6 k + 3}}$ ，结合图 $P (6 k + 3, 1)$ 结构可知，X为 $P (6 k + 3, 1)$ 的一个MENT-集，容易知道 $| X | = 4 k + 2$ ， $m (P (6 k + 3, 1) / X) = 1$ 且 $ω (P (6 k + 3, 1) / X) = 4 k + 2$ ，则 $M E N T (P (6 k + 3, 1)) = \frac{4 k + 3}{4 k + 2}$ 。

情形5 $n = 6 k + 4$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}, u_{6 k + 1} u_{6 k + 2}} \cup {v_{2} v_{3}, v_{5} v_{6}, \dots, v_{6 k + 2} v_{6 k + 3}} \cup {u_{6 k + 4} v_{6 k + 4}}$ ，结合图 $P (6 k + 4, 1)$ 结构可知，X为 $P (6 k + 4, 1)$ 的一个MENT-集，容易知道 $| X | = 4 k + 3$ ， $m (P (6 k + 4, 1) / X) = 1$ 且 $ω (P (6 k + 4, 1) / X) = 4 k + 2$ ，则 $M E N T (P (6 k + 4, 1)) = \frac{2 k + 2}{2 k + 1}$ 。

情形6 $n = 6 k + 5$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}, u_{6 k + 1} u_{6 k + 2}} \cup {v_{2} v_{3}, v_{5} v_{6}, \dots, v_{6 k + 2} v_{6 k + 3}} \cup {u_{6 k + 5} v_{6 k + 5}}$ ，结合图 $P (6 k + 5, 1)$ 结构可知，X为 $P (6 k + 5, 1)$ 的一个MENT-集，容易知道 $| X | = 4 k + 4$ ， $m (P (6 k + 5, 1) / X) = 1$ 且 $ω (P (6 k + 5, 1) / X) = 4 k + 3$ ，则 $M E N T (P (6 k + 5, 1)) = \frac{4 k + 5}{4 k + 3}$ 。

综上所述，定理得证。

定理2.3

对于广义Petersen图 $P (n, 2)$ 有 $M E N T (P (n, 2)) = M E N T (P (n, 1)) = {\begin{cases} \frac{4 k + 1}{4 k}, n = 6 k, k \neq 0 \\ \frac{2 k + 1}{2 k}, n = 6 k + 1, k \neq 0 \\ \frac{4 k + 3}{4 k + 1}, n = 6 k + 2, k \neq 0 \\ \frac{4 k + 3}{4 k + 2}, n = 6 k + 3 \\ \frac{2 k + 2}{2 k + 1}, n = 6 k + 4 \\ \frac{4 k + 5}{4 k + 3}, n = 6 k + 5 \end{cases}$ ，其中 $k \in Z^{+}$ 。

证明显然 $M E N T (P (3, 2)) = M E N T (P (3, 1)) = \frac{3}{2}$ ， $M E N T (P (4, 2)) = 2$ ， $M E N T (P (5, 2)) = \frac{5}{3}$ 。

根据n被6除的余数，分以下六种情形讨论(其中 $k \in Z^{+}$ )。

情形1 $n = 6 k, k \neq 0$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}} \cup {v_{3} v_{5}, v_{6} v_{8}, \dots, v_{6 k} v_{2}}$ ，结合图 $P (6 k, 2)$ 结构(如图3所示)可知，X为 $P (6 k, 2)$ 的一个MENT-集，容易知道 $| X | = 4 k$ ， $m (P (6 k, 2) / X) = 1$ 且 $ω (P (6 k, 2) / X) = 4 k$ ，则 $M E N T (P (6 k, 2)) = \frac{4 k + 1}{4 k}$ 。

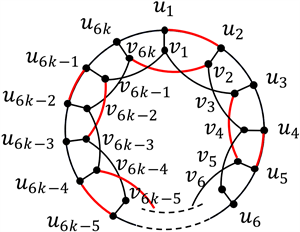
Figure 3. P(6k, 2) and a MENT-set of P(6k, 2)

图3. P(6k, 2)及其一个MENT-集

情形2 $n = 6 k + 1, k \neq 0$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}} \cup {v_{3} v_{5}, v_{6} v_{8}, \dots, v_{6 k - 3} v_{6 k - 1}, v_{6 k + 1} v_{2}} \cup {u_{6 k} v_{6 k}}$ ，结合图 $P (6 k + 1, 2)$ 结构可知，X为 $P (6 k + 1, 2)$ 的一个MENT-集，容易知道 $| X | = 4 k + 1$ ， $m (P (6 k + 1, 2) / X) = 1$ 且 $ω (P (6 k + 1, 2) / X) = 4 k$ ，则 $M E N T (P (6 k + 1, 2)) = \frac{2 k + 1}{2 k}$ 。

情形3 $n = 6 k + 2, k \neq 0$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k - 2} u_{6 k - 1}} \cup {v_{3} v_{5}, v_{6} v_{8}, \dots, v_{6 k} v_{6 k + 2}, v_{6 k + 2} v_{2}} \cup {u_{6 k + 1} v_{6 k + 1}}$ ，结合图 $P (6 k + 2, 2)$ 结构可知，X为 $P (6 k + 2, 2)$ 的一个MENT-集，容易知道 $| X | = 4 k + 2$ ， $m (P (6 k + 2, 2) / X) = 1$ 且 $ω (P (6 k + 2, 2) / X) = 4 k + 1$ ，则 $M E N T (P (6 k + 2, 2)) = \frac{4 k + 3}{4 k + 1}$ 。

情形4 $n = 6 k + 3$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k + 1} u_{6 k + 2}} \cup {v_{3} v_{5}, v_{6} v_{8}, \dots, v_{6 k} v_{6 k + 2}, v_{6 k + 3} v_{2}}$ ，结合图 $P (6 k + 3, 2)$ 结构可知，X为 $P (6 k + 3, 2)$ 的一个MENT-集，容易知道 $| X | = 4 k + 2$ ， $m (P (6 k + 3, 2) / X) = 1$ 且 $ω (P (6 k + 3, 2) / X) = 4 k + 2$ ，则 $M E N T (P (6 k + 3, 2)) = \frac{4 k + 3}{4 k + 2}$ 。

情形5 $n = 6 k + 4$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k + 1} u_{6 k + 2}} \cup {v_{3} v_{5}, v_{6} v_{8}, \dots, v_{6 k} v_{6 k + 2}, v_{6 k + 4} v_{2}} \cup {u_{6 k + 3} v_{6 k + 3}}$ ，结合图 $P (6 k + 4, 2)$ 结构可知，X为 $P (6 k + 4, 2)$ 的一个MENT-集，容易知道 $| X | = 4 k + 3$ ， $m (P (6 k + 4, 2) / X) = 1$ 且 $ω (P (6 k + 4, 2) / X) = 4 k + 2$ ，则 $M E N T (P (6 k + 4, 2)) = \frac{2 k + 2}{2 k + 1}$ 。

情形6 $n = 6 k + 5$ 。

令 $X = {u_{1} u_{2}, u_{4} u_{5}, \dots, u_{6 k + 1} u_{6 k + 2}} \cup {v_{3} v_{5}, v_{6} v_{8}, \dots, v_{6 k + 3} v_{6 k + 5}, v_{6 k + 5} v_{2}} \cup {u_{6 k + 4} v_{6 k + 4}}$ ，结合图 $P (6 k + 5, 2)$ 结构可知，X为 $P (6 k + 5, 2)$ 的一个MENT-集，容易知道 $| X | = 4 k + 4$ ， $m (P (6 k + 5, 2) / X) = 1$ 且 $ω (P (6 k + 5, 2) / X) = 4 k + 3$ ，则 $M E N T (P (6 k + 5, 2)) = \frac{4 k + 5}{4 k + 3}$ 。

综上所述，定理得证。

3. 结论

本文在已知混合边邻域粘连度概念的基础上给出了广义Petersen图的混合边邻域粘连度的计算公式。闫伟 [17] 已指出混合边邻域粘连度的区分度较好，刻画某些网络的抗毁性更为精确。一般图的混合边邻域粘连度计算比较复杂，但一些具有特殊结构的图类，如联图、Harary图、树等的混合边邻域粘连度算法值得深入研究。

NOTES

^*通讯作者。

参考文献

[1]	Gunther, G. (1985) Neighbor-Connectivity in Regular Graphs. Discrete Applied Mathematics, 11, 233-243. https://doi.org/10.1016/0166-218X(85)90075-7
[2]	陈忠, 李银奎. 完全k叉树的粘连度[J]. 纯粹数学与应用数学, 2013, 29(5): 484-488.
[3]	Gu, M.M., Pai, K.J. and Chang, J.M. (2023) Subversion Analyses of Hierarchical Networks Based on (Edge) Neighbor Connectivity. Journal of Parallel and Distributed Computing, 171, 54-65. https://doi.org/10.1016/j.jpdc.2022.09.010
[4]	Cozzens, M.B. and Wu, S.S.Y. (1995) Extreme Values of Edge-Neighbor-Connectivity. Ars Combinatoria, 39, 199-210.
[5]	Zhao, X.B., Zhang, Z. and Ren, Q. (2011) Edge Neighbor Connectivity of Cartesian Product Graph G x K2. Applied Mathematics and Computation, 217, 5508-5511. https://doi.org/10.1016/j.amc.2010.12.022
[6]	Bacak, T.G. and Kirlangic, A. (2013) Neighbor Integrity of Trans-formation Graphs. International Journal of Foundations of Computer Science, 24, 303-317. https://doi.org/10.1142/S0129054113500056
[7]	Cozzens, M.B. and Wu, S.S.Y. (1997) Bounds of Edge-Neighbor-Integrity of Graphs. Australasian Journal of Combinatorics, 15, 71-80.
[8]	Wei, Z.T., Qi, N.N. and Yue, X.K. (2016) Vertex-Neighbor-Scattering Number of Bipartite Graphs. International Journal of Foundations of Computer Science, 27, 501-509. https://doi.org/10.1142/S012905411650012X
[9]	Wei, Z.T., Qi, N.N. and Yue, X.K. (2013) Computing the Edge-Neighbor-Scattering Number of Graphs. Zeitschrift fur Naturforschung A, 68, 599-604. https://doi.org/10.5560/zna.2013-0059
[10]	Liu, Y., Wei, Z.T., Shi, J. and Mai, A.C. (2016) A Polynomial Algo-rithm of Edge-Neighbor-Scattering Number of Trees. Applied Mathematics and Computation, 283, 1-5. https://doi.org/10.1016/j.amc.2016.02.021
[11]	杨静婷. 图的邻域坚韧度研究[D]: [硕士学位论文]. 西安: 西安建筑科技大学, 2017.
[12]	杨玉成. 图的边邻域坚韧度研究[D]: [硕士学位论文]. 西安: 西安建筑科技大学, 2019.
[13]	Feng, X., Wei, Z.T. and Yang, Y.C. (2022) Edge Neighbor Toughness of Graphs. Axiom, 11, Article 248. https://doi.org/10.3390/axioms11060248
[14]	Bacak-Turan, G. and and Oz, E. (2017) Neighbor Rupture Degree of Transformation Graphs Gxy-. International Journal of Foundations of Computer Science, 28, 335-355. https://doi.org/10.1142/S0129054117500216
[15]	Aslan, E. (2013) Edge-Neighbor-Rupture Degree of Graphs. Journal of Applied Mathematics, 2013, Article ID: 783610. https://doi.org/10.1155/2013/783610
[16]	Kurkcu, O.K. and Aslan, E. (2018) A Comparison between Edge Neighbor Rupture Degree and Edge Scattering Number in Graphs. International Journal of Foundations of Computer Science, 29, 1119-1142. https://doi.org/10.1142/S0129054118500247
[17]	闫伟, 魏宗田. 图的混合边邻域粘连度[J]. 山西大学学报(自然科学版): 1-12. https://kns.cnki.net/kcms2/article/abstract? v=f2Ae6OvU-JLJXPF5CLFWKeefdu2cPA_nGciw2tR-goYvPP efp1-MjlsUUw-LCN2UFNVZdRrah1WeBktQMr6JJApMG5hy3rqWVhzHlOJ65LG_ bUcLSBA2Qj0lToTToSBppxTXc4Ph71U=&uniplatform=NZKP T&language=CHS, 2023-10-28.
[18]	毛华, 赵小娜, 史田敏. 多部图的最大匹配算法[J]. 郑州大学学报(理学版), 2013, 45(1): 27-29, 37.
[19]	Bondyj, A. and Murty, U.S.R.M. (2008) Graph Theory. Springer, London.
[20]	魏宗田, 刘勇, 杨威, 等. 网络抗毁性[M]. 西安: 西安交通大学出版社, 2015.

为你推荐

友情链接