基于层间影响的时序网络节点重要性识别

Importance Identification of Nodes in Sequential Network Based on Inter-Layer Influence

摘要: 现实生活中，复杂网络具有动态性和时变性，识别时序网络中的重要节点相比于静态网络更加具有挑战性。在本文中，我们提出了一种基于层间影响的超邻接矩阵在时序网络中的节点重要性识别方法。首先，我们定义了层间影响系数，其次考虑了时序网络层内和层间的关系构建了时序超邻接矩阵(TSAM)利用特征向量中心性对节点的中心性指标进行估。在多个实现数据集上的结果显示：相比经典的方法SAM以及SSAM，使用提出的算法得到的Kendall’s τ值在各时间层上均有显著提高，结果表明时序引力模型的度量对于时序网络的节点重要性度量具有十分重要的意义。

Abstract: In real life, complex networks are dynamic and time-varying, and it is more challenging to identify the important nodes in the temporal network than static networks. In this paper, we propose a method to identify the importance of nodes in temporal networks based on the super-adjacency matrix based on inter-layer influence. First, we define the inter-layer influence coefficient, and then we consider the relationship between the intra-layer and inter-layer of the temporal network to construct the temporal super-adjacency matrix (TSAM) to estimate the centrality index of the node using the centrality of the feature vector. The results on multiple implementation data sets show that compared with the classical methods SAM and SSAM, Kendall’s τ obtained by using the proposed algorithm. The results show that the measurement of temporal gravity model is very important for the measurement of node importance in temporal networks.

1. 引言

随着科学技术不断发展，针对传统单层网络研究网络科学的方法应接不暇。有效识别复杂网络中的重要节点对于阻止病毒蔓延 [1] 、提升铁路网络鲁棒性 [2] 、识别微博网络中重要用户 [3] [4] 、评价科研工作者影响力 [5] 、判断社交网络中有影响力的人物 [6] 、识别重要新闻内容 [7] 等方面具有重要的作用。刘建国等人 [8] 于2013年对复杂网络中节点重要性研究从网络结构和传播动力学方面进行描述，并指出中心性指标的优缺点。任晓龙等人 [9] 将复杂网络中节点排序算法主要分为四类，从节点的局部信息、拓扑结构等方面进行阐述并介绍了各算法的优缺点、应用场景以及评价标准。由于近年来复杂网络的快速发展，各种算法层出不穷，由此可见，研究复杂网络的理论和方法对于重要节点识别提供了多种算法，同时重要节点的挖掘对于网络科学的理论研究和应用也有重要的意义和价值。

网络表示对于描述大量复杂系统的结构是有用的。然而，大多数实际的系统不同于传统的静态网络，它们都有都是时变的，时间顺序已经被证明对网络结构和信息传播有很大影响 [10] [11] 。由于时序网络 [12] 考虑事件发生的顺序，可以更准确地刻画复杂系统的演化特征 [13] ，可以更加准确地描述节点之间的交互顺序和交互关系 [14] ，因此现实生活中对于时序网络的研究至关重要。

现有的时序网络中重要节点的大多数度量都是扩展了静态网络的度量 [15] 。因此，各种方法要么将时序网络集成到静态网络中，形成聚合网络；要么随着时间的推移将时序网络分割成一系列静态时间窗口。即，考虑时序网络的中心性度量可以按如下方式进行分析。首先，在给定的时间下，将时序网络划分为多个时间窗口。每个时间窗口都被视为一个静态网络。然后获得每个节点和时间窗的中心性得分，节点最终中心性得分是各时间窗得分的平均值 [16] 。尽管与静态中心性方法相比，此类方法可以更好地识别重要节点，但它们可能会丢失时间信息，例如节点交互的时间顺序。

为了更加准确地表示时序网络随时间演变的结构特征以及考虑不同时间窗口之间的相互影响。Taylor等人 [17] 提出了一种基于时序网络相邻时间层之间的层间相互关系进行分析，首先建立超邻接矩阵(Supra-Adjacency Matrix, SAM)来描述时序网络的不同时间曾之间的层间关系以及单个时间层内的关系，随后基于特征向量的中心性指标定义了适用于时序网络中的节点重要性评判指标。然而，他们提出的SAM模型中时序网络的构建仅将相邻层间各个对应节点之间的连接关系表示为某一特定参数，这样的做法无疑是忽略了不同时间窗之间节点连接关系的差异性。因此，考虑到不同时间窗口之间的层间连接关系具不统一，需要进一步改进SAM方法，杨剑楠等人 [18] 对SAM进行了改进，提出SSAM方法对时序网络中重要节点进行识别。受他们的启发，我们对时序网络的各时间层进行了定量的分析，通过充分考虑各时间层之间的影响来构造时序超邻接矩阵，并与传统方法进行对比显示了我们方法的优越性；进而引入特征向量中心性对节点的得分进行量化。

除此之外，由于牛顿所开创的万有引力定律在物理学界得到了巨大的成就，且简单易懂，覆盖面广。受万有引力定律任何物体之间都具有相互吸引力的影响，我们将万有引力定律引入到复杂网络中探索网络中节点的重要性。我们假设，这个力的大小取决于网络中的节点的属性呈正相关，与它们之间的时序距离的平方呈负相关。关于节点的属性，Bi等人 [19] 已经探索了节点的度中心性 [20] 、介数中心性 [21] 、紧密度中心性 [22] 以及PageRank中心性 [23] ，本文将研究节点的特征向量中心性作为节点属性，并以时序距离作为来表示距离，融入到引力模型进而来判断重要节点。

2. 相关工作

在本节中，我们主要介绍了时序网络基本概念，包括时序网络的表示、时序距离；其次，我们简要介绍了基准中心性度量方法；最后，我们介绍了几种现有的时序网络的中心性指标。

2.1. 基本符号和定义

时间间隔 $\left[1,T\right]$ 上的时序网络通常可以表示为 $G^T=\left(V,E^T\right)$ 。该网络是由 $N=\left|V\right|$ 个节点集合V和时间序列集合 $E^T$ 组成。对于每一个时间切片 $e\in E^T$ 是由一个三元组 $\left(v_i,v_j,t\right)$ 组成，其表示为在时间t下节点 $v_i$ 和 $v_j$ 之间的交互。对于每一个时间窗口 $t\in \left[1,T\right]$ ，其邻接矩阵为 $A_t$ ，其中 $A_t\left(i,j\right)=1$ 表示节点 $v_i$ 和节点 $v_j$ 在时间t时存在交互； $A_t\left(i,j\right)=0$ 表示节点 $v_i$ 和节点 $v_j$ 在时间t时不存在交互。

时序网络的窗口数由时间间隔 $\Delta t$ 决定，网络窗口由 $G_1,G_2,\cdots ,G_n$ 给出，当 $\Delta t$ 很小时，时间网络将会有多个窗口。如果当 $\Delta t=T$ 时，我们得到相应的静态网络 $G^T$ ，表示为 $G=\left(V,E\right)$ 。如果节点在 $G^T$ 中至少有一个次接触，一对节点 $v_i,v_j$ 通过链路 $\left(v_i,v_j\right)\in E$ ，则G的邻接矩阵表示为A，其中如果节点 $v_i$ 和 $v_j$ 连接，则 $A\left(i,j\right)=1$ ，否则 $A\left(i,j\right)=1$ 。

我们考虑图1所示的时序网络的示例。图1(a)示出了具有4个节点和 $T=4$ 个时间窗的时序网络。通常设置 $t=1$ 时，时序网络包含四个时间窗， $G_1,G_2,G_3,G_4$ 。图1(b)显示了相应的聚合网络G。

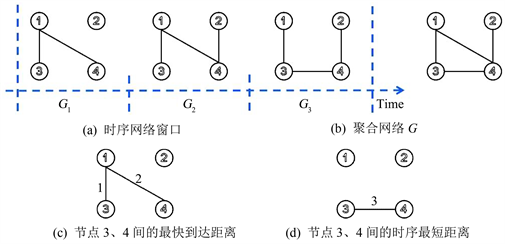
Figure 1. Temporal network $G^T=\left(V,E^T\right)$ with 4 nodes and 3 time windows, (a) is the static time window, (b) is the aggregation network of each static time window, (c) is the fastest arrival path between 3 and 4 nodes, and (d) is the shortest time series path between 3 and 4 nodes. The corresponding fastest distance of arrival and the shortest distance of the time series are 2 and 1, respectively

图1. 时序网络 $G^T=\left(V,E^T\right)$ ，有4个节点，3个时间窗口，(a) 是静态时间窗 $G_1,G_2,G_3,G_4$ ，(b) 是各静态时间窗口的聚合网络G，(c) 是3和4节点间的最快到达路径，(d) 是3和4节点间的时序最短路径。相应的最快到达距离和时序最短距离分别为2和1

2.2. 时序路径

给定具有n个时间窗的时序网络 $G^T=\left(V,E^T\right)$ ，时序路径是节点序列 $S=\langle v_1,v_2,\cdots ,v_k,v_{k+1}\rangle$ ，其中事件 $\left(v_i,v_j,t_i\right)\in E^T,1\le i\le k,t_i\le t_{i+1}$ 是S上的第i个时间窗口 $v_i$ 和 $v_j$ 之间是否发生的交互。因此， $t_1$ 是S的初始时间， $t_k$ 是S的最终时间。给定时间间隔 $\left[t_a,t_b\right]$ ， $v_i$ 是初始节点， $v_j$ 是最终节点， $\forall v_i,v_j\in V$ 。我们考虑时序路径的两种不同定义：最快到达路径和时间最短路径。这两种路径在时序网络中具有代表性。

最快到达路径

最快到达路径 [24] 初始节点 $v_i$ 和最终节点 $v_j$ 之间最快到达的路径是时间路径，最小持续时间从 $t=1$ 开始计算。因此，最快到达路线是从初始节点 $v_i$ 到最终节点 $v_j$ 的路径，在一段时间内经过的时间最短，并且在每个时间窗口中信息的每次传输只能经过一条路径。如果 $t_{end}\left(S\right)=\min \left\{t_{end}\left(S^{\prime }\right)|S^{\prime }\in S\left(v_i,v_j,\left[t_a,t_b\right]\right)\right\}$ ， $S\in S\left(v_i,v_j,\left[t_a,t_b\right]\right)$ 是最快到达路径，节点 $v_i$ 和 $v_j$ 之间的最快到达距离为对应最快到达路径的路径长度。图1(a)中各节点之间的最快到达路径见表1。

Table 1. In Figure 1(a), the fastest path between nodes, and the pairs of nodes without the fastest path are depresented ∞

表1. 图1(a)中各节点之间的最快到达路径，没有最快到达路径的节点对表示为 $\infty$

2.3. 时序网络的中心性指标

2.3.1. SAM时序网络模型

Taylor等人 [17] 采用基于多层时序网络模型的多层耦合网络分析方法，将时序网络建模为NT × NT超邻接矩阵(Super-Adjacency Matrix, SAM)，其表达式如下：

$\text{SAM}=\left[\begin{array}{cccc}{A}^{\left(1\right)}& \omega I& 0& \cdots \\ \omega I& A^{\left(2\right)}& \omega I& \cdots \\ 0& \omega I& A^{\left(3\right)}& \cdots \\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$ (1)

$A^{\left(1\right)},A^{\left(2\right)},\cdots ,A^{\left(t\right)}\in {ℝ}^{N\times N}$ 代表各时间层内的邻接矩阵，此外， $\omega I$ 表示层间连接关系，其中层间耦合 $\omega$ 是用于调整每个时间层网络耦合关系强度的可调参数，I是单位矩阵。因为这里只考虑相邻时间层中相同节点之间的连接关系，所以矩阵的其他部分都是0。

Taylor等人只研究了 $\omega \ge 0$ 的情况，即层间耦合被认为是正的。例如，当 $\omega \to 0^{+}$ 时，各层变得不耦合；否则，当 $\omega \to \infty$ 时，层间耦合非常强，层间权重控制层内连接。当层内连接关系不变时，层间关系强度的变化对网络效率有显著影响。在这种情况下，SAM最大奇异值对应的特征向量表示每个节点 $v_i$ 在每个时间t的中心性。

2.3.2. SSAM时序网络模型

杨剑楠等人 [18] 在SAM的基础上进行了改进，特别是对SAM的层间连接关系进行了改进。他们考虑到同一节点在相邻时间层之间的连接关系与其在两个时间层上的持续出现度以及节点的邻居关系层间相似程度有关。因此，他们引入了邻居拓扑重叠系数来确定层间连接关系。这样，改进后的方法被称为基于层间相似性的超邻接矩阵(Supra-Adjacency Matrix based on Layer Similarity, SSAM)。通过使用SSAM，可以更准确地描述时序网络的结构演变和动力学过程。SSAM时序网络模型具体表示形式如下：

$\text{SSAM}=\left[\begin{array}{cccc}{A}^{\left(1\right)}& C^{\left(1,2\right)}& 0& \cdots \\ C^{\left(1,2\right)}& A^{\left(2\right)}& C^{\left(2,3\right)}& \cdots \\ 0& C^{\left(2,3\right)}& A^{\left(3\right)}& \cdots \\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$ (2)

$A^{\left(1\right)},A^{\left(2\right)},\cdots ,A^{\left(t\right)}\in {ℝ}^{N\times N}$ 代表各时间层内的邻接矩阵， $C^{\left(1,2\right)},C^{\left(2,3\right)},\cdots ,C^{\left(t-1,t\right)}$ 分别表示相邻时间层的连接关系，且 $C^{\left(t-1,t\right)}$ 为 $N\times N$ 的对角矩阵，可表示为 $C^{\left(t-1,t\right)}=diag\left(c_1^{\left(t-1,t\right)},c_2^{\left(t-1,t\right)},\cdots ,c_N^{\left(t-1,t\right)}\right)$ ， $c_i^{\left(t-1,t\right)}$ 为节点 $v_i$ 的在t − 1与t时间窗口的邻居拓扑重叠系数，表示为：

$c_i^{\left(t-1,t\right)}=\frac{{\displaystyle \underset{j}{\sum }{a}_{ij}\left(t-1\right)a_{ij}\left(t\right)}}{\sqrt{\left[{\displaystyle \underset{j}{\sum }{a}_{ij}\left(t-1\right)}\right]\left[{\displaystyle \underset{j}{\sum }{a}_{ij}\left(t\right)}\right]}}$ (3)

其中 $a_{ij}\left(t\right)$ 表示时间窗口t对应的网络图中的连边关系，如果节点 $v_i$ 和 $v_j$ 有连边，则 $a_{ij}\left(t\right)=1$ ，否则为0。其分子表示的含义为，只有节点 $v_i$ 和 $v_j$ 同时在t − 1与t时间窗口存在连边，才有 $a_{ij}\left(t-1\right)a_{ij}\left(t\right)=1$ ，其它情况均为0。

邻居拓扑重叠系数描述了节点与其邻居持续出现的连边的层间相似性。该系数越大表示节点持续出现在两个相继时间层，且邻接关系保持稳定；反之，系数越小表示节点为持续出现两个相继时间层或相邻时间层上邻接关系较不稳定。

3. 基于层间影响的超邻接矩阵

1) 构建时序超邻接矩阵(Temporal Super-Adjacency Matrix, TSAM)

受SAM以及SSAM的启发，本文构建了时序超邻接矩阵(TSAM)。其思想是，在时序网络中，由于将时序网络划分为各个时间切片，每个时间切片构成一个网络，由于前面时间切片中的连接关系可能会对之后的时间切片产生影响，并且这种影响不仅仅存在于相邻的两个时间切片中，跨时间切片同样会产生影响(例如，第一个时间切片会对之后所有的时间切片产生一定的影响)。除此以外，因此，我们在邻居拓扑重叠系数的基础上，对各层影响值加入参数来量化它们之间的影响，且各时间切片之间的影响随着间隔的增加存在着衰减效应，因此将TSAM设置为如下所示：

$\text{TSAM}=\left[\begin{array}{cccc}{A}^{\left(1\right)}& I^{\left(1,2\right)}& \cdots & I^{\left(1,t\right)}\\ 0& A^{\left(2\right)}& \ddots & I^{\left(2,t\right)}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & A^{\left(t\right)}\end{array}\right]$ (4)

其中 $A^{\left(1\right)},A^{\left(2\right)},\cdots ,A^{\left(t\right)}\in {ℝ}^{N\times N}$ 代表各时间层内的邻接矩阵， $I^{\left(1,2\right)},I^{\left(2,3\right)},\cdots ,I^{\left(t-1,t\right)}$ 分别表示不同层节点之间的影响；此外， $\beta$ 设置为 $\beta =t_2-t_1-1$ ， $t_1,t_2$ 表示各自代表的时间切片编号，减1的目的是认为相邻的两个时间窗间的影响不存在衰减，即相邻两个时间切片的影响为 $I^{\left(t-1,t\right)}$ ，与SSAM模型呼应； $\alpha$ 为可调节的衰减因子。除此以外，我们将TSAM设置为上三角矩阵，其思想是只认为前面的时间切片会对后面的时间切片产生影响。

$I_i^{\left(t-1,t\right)}=\frac{{\displaystyle \underset{j}{\sum }{a}_{ij}\left(t-1\right)+{\displaystyle \underset{j}{\sum }{a}_{ij}\left(t\right)-{\displaystyle \underset{j}{\sum }{a}_{ij}\left(t-1\right)a_{ij}\left(t\right)}}}}{N}$ (5)

其中 $a_{ij}\left(t\right)$ 表示时间窗口t对应的网络图中的连边关系，如果节点 $v_i$ 和 $v_j$ 有连边，则 $a_{ij}\left(t\right)=1$ ，否则为0。其分子表示的含义为，只有节点 $v_i$ 和 $v_j$ 同时在t − 1与t时间窗口存在连边，才有 $a_{ij}\left(t-1\right)a_{ij}\left(t\right)=1$ ，其它情况均为0；N表示聚合网络中的节点数。

图1对应的时序超邻接矩阵如下所示：

$\text{TSAM}=\left[\begin{array}{cccccccccccc}0& 0& 1& 1& \frac{1}{2}& 0& 0& 0& \frac{1}{2}& 0& 0& 0\\ 0& 0& 0& 0& 0& \frac{1}{4}& 0& 0& 0& \frac{1}{4}& 0& 0\\ 1& 0& 0& 0& 0& 0& \frac{1}{2}& 0& 0& 0& \frac{1}{2}& 0\\ 1& 0& 0& 0& 0& 0& 0& \frac{1}{2}& 0& 0& 0& \frac{3}{4}\\ 0& 0& 0& 0& 0& 0& 1& 1& \frac{1}{2}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& \frac{1}{4}& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& \frac{1}{2}& 0\\ 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& \frac{3}{4}\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0\end{array}\right]$ (6)

2) 计算特征向量中心性

根据所构建的时序超邻接矩阵，进一步计算出其最大特征值对应的特征向量，即为各时间切片内各节点的特征向量中心性 [20] 。

本文针对静态网络中的特征向量中心性进行拓展，利用特征向量中心性对时序网络的节点进行打分，即对上文构建的超邻接矩阵TSAM求主特征向量 $\nu ={\left\{v_1,v_2,\cdots ,v_{NT}\right\}}^{\text{T}}$ 。这样，向量 $\nu$ 的第 $N\left(t-1\right)+i$ 个项即表示第t个时间层上的节点 $v_i$ 的特征向量中心性，记为N × T的矩阵 $E={\left\{e_{it}\right\}}^{N\times T}$ ，则 $e_{it}=v_{N\left(t-1\right)+i}$ ，其中 $e_{it}$ 为矩阵E的第i行第t列元素，表述为第t个时间层上的节点i的特征向量中心性。

4. 基于时序网络的时序引力模型评估方法

本文使用时序网络上的网络效率进行时序引力模型的性能评估。网络效率旨在确定节点在信息交换中的作用。本文并使用Kendall’s τ相关系数比较了从时序引力模型中获得的节点重要性得分和性能评估方法(即网络效率)。较高的Kendall’s τ相关系数表明，本文提出的模型可以更加准确的识别时序网络中的重要节点。本文首先定义了时序网络上的网络效率，并给出了时序引力模型识别时序网络中重要节点的结果，通过Kendall’s τ相关系数来判断本文模型的优劣。

4.1. 网络效率 [25]

为进一步检验该方法对节点重要性的排序效果，本文通过删除节点后网络连通性的变化程度来评价节点重要性排序结果。通常认为，删除节点后，网络连通性变化越大，则被删除的节点在网络中越重要；反之，则节点重要性相对较低。网络效率是评判时序网络连通性的一个重要方法。对于网络效率，我们假设网络中的信息仅通过最快到达路径传输。效率衡量网络上信息交换的质量。我们将时态网络 $G^T$ 的网络效率定义如下：

$\epsilon \left(G^T\right)=\frac{1}{N\left(N-1\right)}{\displaystyle \underset{v_i\ne v_j\in G^T}{\sum }\frac{1}{d_{ij}}}$ (7)

其中， $d_{ij}$ 是节点 $v_i$ 和 $v_j$ 之间的时序距离。两个节点之间的时序距离可以由最快到达距离或时间最短距离定义。

如果网络断开连接，从时序网络中删除节点可能会降低网络效率。因此，节点移除后的效率可以反映节点在时间网络中的重要性。效率降低越大，表明节点在结构影响方面的重要性越高。让 $G^T\backslash v_i$ 表示移除节点 $v_i$ 及其所有关联联系人后的时间网络。 $G^T$ 的网络效率与 $G^T\backslash v_i$ 的网络效率之差定义为节点 $v_i$ 在网络效率方面的重要性得分 [26] ：

$NE\left(v_i\right)=\epsilon \left(G^T\right)-\epsilon \left(G^T\backslash v_i\right)$ (8)

式中， $NE\left(v_i\right)$ 表示节点 $v_i$ 的网络效率。在每一个时间切片用删除节点后网络效率与原网络效率的差值作为该时间层节点重要性的验证方法，依次删除各个时间层的节点后重新计算网络的网络效率，最终得到一个 $N\times T$ 的矩阵。

4.2. 肯德尔系数

肯德尔系数 [27] 是衡量两个序列之间相关性强度的指标。本文利用肯德尔系数对时序引力模型矩阵X以及评估指标矩阵Y进行相关性分析。分别考虑不同时间窗口 $t,t\in T$ 各节点的得分 $x^t$ 以及评估指标 $y^t$ ， $x^t,y^t$ 是两个具有N个元素的序列， $x^t=\left(x_1^t,x_2^t,\cdots ,x_N^t\right)$ 和 $y^t=\left(y_1^t,y_2^t,\cdots ,y_N^t\right)$ 。两个元组 $\left(x_i^t,y_i^t\right)$ 和 $\left(x_j^t,y_j^t\right)$ $\left(i\ne j,1\le i,j\le N,t\in T\right)$。如果 $x_i^t>x_j^t$ 的同时 $y_i^t>y_j^t$ 或 $x_i^t<x_j^t$ 的同时 $y_i^t<y_j^t$ ，则一致。如果 $x_i^t>x_j^t$ 和 $y_i^t<y_j^t$ 或 $x_i^t<x_j^t$ 和 $y_i^t>y_j^t$ ，则它们不一致。如果 $x_i^t=x_j^t$ 或 $y_i^t=y_j^t$ ，则该对既不一致也不不一致。两个序列 $x^t$ 和 $y^t$ 的肯德尔系数可以计算为：

$\tau =\frac{2\left(n_{+}-n_{-}\right)}{N\left(N-1\right)}$ (9)

其中 $n_{+}$ 和 $n_{-}$ 分别表示一致对和不一致对的数量。可以看出， $\tau$ 超过零的程度表明相关性的强度。

5. 实验结果和分析

5.1. 数据描述

我们在以下经验时间网络数据集上评估时间重力模型的性能。网络的一些详细属性如表2所示。

Workspace [28] 为法国某公司通过移动射频设备获取的92位公司员工之间每天面对面交互产生的交互数据，时间从2013年6月24日到2013年7月3日，按天切分数据；Workplace [29] 该数据集包含2015年在法国一栋办公楼中测量的个人之间接触的时间网络；LH10 [29] 为一家医院的面对面交互数据集；EEU1 [30] 该网络是使用来自欧洲一家大型研究机构的电子邮件数据生成的。该数据集还包含节点的“真实”社区成员身份。

Table 2. Basic statistical characteristics of empirical networks

表2. 实证数据基本统计特征

5.2. 结果分析

从图2的结果图可以观察到：

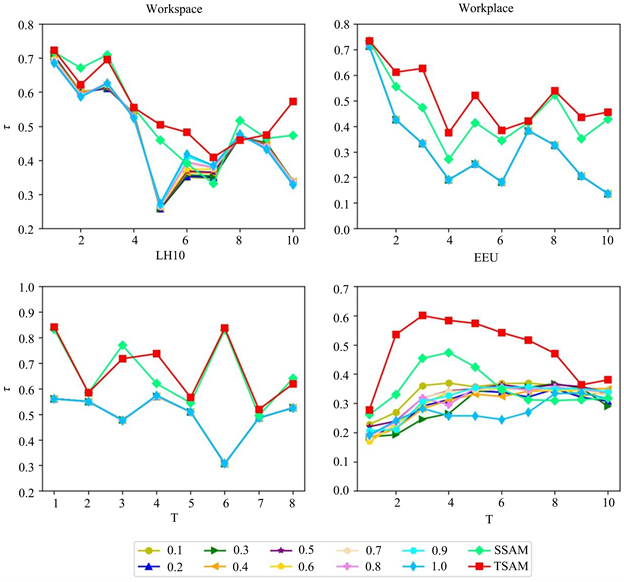
Figure 2. Results of Kendall’s coefficient under the efficiency of time-series networks

图2. 时序网络效率下肯德尔系数的结果

1) 在四组由实证数据构建的时序网络，由于SAM模型仅考虑了相邻层间的层间影响，且层间影响使用不同的参数来表示各个相应节点之间的层间关系，因此SAM模型在从0~1之间的参数下得到的肯德尔相关系数的结果近乎无差。特别是在Workplace和LH10这两个数据集中，图2的结果显示这种情况尤为显著。换句话说，在SAM模型下，对于相邻时间层，使用节点的特征向量中心性并不能明显区分各个时间窗口的系欸但排序结果；

2) 由TSAM模型得到的肯德尔系数结果在大部分时间窗口下比SSAM模型以及SAM模型的排序结果高。这表明基于层间相似性的TSAM模型考虑了不同时间窗口不同节点的差异且考虑了跨层之间的层间影响，能更准确地描述时序网络中各个时间窗口的节点重要性排序。尤其是在Workplace和EEU数据集中，TSAM方法的结果尤为显著。具体来说，对于四组实证数据，TSAM模型相比SAM模型在各时间层上的肯德尔系数结果平均提高了9.94%、15.37%、11.69%和20.51%；

3) 然而Workspace数据的存在个别时间层SSAM方法的结果略低于SAM方法，例如6、7和9三个时间窗口。然而，TSAM模型通过改进这种差异，得到的准确率普遍高于SAM模型。换句话说，TSAM模型在这些时间层上能够更准确地描述时序网络的结构和节点重要性；

4) 对于四个数据集，TSAM模型的准确率相较于SSAM模型以及SAM模型均有较大的提升，相较于SSAM模型平均提升了2.09%、5.9%、1.3%以及13.01%。

5) 根据给出的表3的肯德尔系数指标，我们对TSAM模型进行如下的具体分析：

Table 3. Kendall’s coefficients of TSAM model and SSAM model in each time window

表3. TSAM模型与SSAM模型在各时间窗口的肯德尔系数

a) 整体趋势：针对于Workplace数据集，计算这十个时间窗口的平均值为0.5109；针对于Workspace数据集，十个时间窗口的平均值为0.5501；针对LH10数据集，八个时间窗口的平均值为0.6782；针对于EEU数据集，十个时间窗口的平均值为0.4848。针对与SSAM模型均有显著提升。

b) 相邻时间窗口的比较：针对于Workplace数据集，观察相邻时间窗口之间的肯德尔系数指标，可以发现在某些相邻时间窗口之间存在较大的变化，例如从t = 3到t = 4的指标从0.627下降到0.376；针对于Workspace数据集，可以观察到从t = 2到t = 3的指标从0.6226增加到0.6955；针对LH10数据集，从t = 1到t = 2的指标从0.5853增加到0.7181。这表明在这两个时间窗口中，节点的重要性发生了显著的变化；针对于EEU数据集，可以观察到从t = 1到t = 2的指标从0.2791增加到0.5358。由此可以发现，在时序网络中，不同时间窗的重要节点有一定的差异，这也就意味着，随着时间的变化，重要节点也随之变化。

6. 结论

识别网络中的重要节点一直是复杂网络的热点问题，节点重要性研究对于理解和优化各种复杂网络的结构和功能具有重要意义。本文将时序网络进行切分处理，继而使用时间窗内的邻接关系以及不同时间层之间的层间连接关系共同来表述时序网络，其次考虑不同节点的差异性及相继时间层的时序相关性，用节点的邻居拓扑重叠系数来表示时序网络中不同时间窗之间的连接关系，提出了一种时序超邻接矩阵(TSAM)，同时利用特征向量中心性的思想来度量时序网络中不同时间窗的节点的重要性。最后，本文利用时序网络的评价方法之一节点删除法，通过遍历网络中的节点，计算删除节点前后时序网络中时序全局效率的变化情况，从而评估TSAM模型对节点重要性排序的效果优劣。

在实证数据集上的结果表明，相较于传统的SAM模型以及SSAM模型，本文提出的TSAM模型能更加准确的识别网络中的重要节点；同时TSAM模型一方面避免了对不同时间窗之间的参数研究，另一方面由于考虑了不同节点在相邻时间窗以及跨时间窗间连接关系具有差异，同时考虑了时间对节点影响的有向性，用基于节点的层间相似度构建时序超邻接矩阵。综上所述，相比经典的模型SAM以及SSAM，使用提出的算法得到的Kendall’s τ值在各时间层上均有显著提高，结果表明时序引力模型的度量对于时序网络的节点重要性度量具有十分重要的意义。