均值方差模型改进及实证检验

Improvement and Empirical Testing of Mean Variance Model

摘要: 如何能够在投资中有效地降低风险并获得可观收益，一直是投资者关注的问题。本文根据Markowitz经典的投资组合理论，对均值–方差模型、均值–下半方差模型和组合偏差模型进行了介绍，利用上证50成分股2021年数据求解投资组合，2022年数据进行回测并比较上述模型与等比例投资的表现。结果显示：1) 从投资组合的表现来看，组合偏差 > 均值–下半方差 > 均值–方差 > 等比例投资；2) 衡量投资组合的风险时应当将超额收益的因素考虑进去；3) 衡量投资组合风险时下半方差是主要的因素。

Abstract: How to effectively reduce risks and achieve considerable returns in investment has always been a concern for investors. This article introduces the mean variance model, mean lower half variance model, and portfolio bias model based on Markowitz’s classic portfolio theory. The investment portfolio is solved using the 2021 data of the Shanghai Stock Exchange’s 50 component stocks, and the 2022 data is backtested to compare the performance of the above models with proportional investments. The results show that: 1) From the performance of the investment portfolio, portfolio bias > mean lower half variance > mean variance > proportional investment; 2) When measuring the risk of an investment portfolio, the factor of excess returns should be taken into account; 3) The lower half variance is the main factor in measuring portfolio risk.

1. 引言

投资组合一直是金融学方面关注的重点问题，每个投资者都想知道，如何将财富分配在不同的金融资产上能够获得更大的收益并承担更小的风险。Markowitz在1952年提出了使用收益率的方差来表示风险的方法，从而创立了著名的均值–方差理论，很多学者便在此基础上研究投资组合问题。用方差来表示投资组合的风险，意味着收益率不论是向上偏离还是向下偏离都被视为风险，但是在实际的投资中投资者可能只将向下偏离，即收益率未达到预期的情况视为风险，超过预期收益率的情况被看作超额收益，因此单纯用方差来表示投资组合的风险是存在一定的偏误的。Markowitz在1959年提出了使用下半方差来表示投资组合的风险，更符合投资市场的现实情况，许多学者构建了均值–下半方差模型，对均值–方差模型进行了扩展。李晓和李红丽(2011) [1] 用我国2007年的股票市场数据对均值–方差模型和均值–下半方差模型进行实证分析，结果显示均值–下半方差模型的可行域包含了均值–方差的可行域，因此半方差模型能够在更大的范围内选择最优解，投资结果会优于均值–方差模型。卫海英和徐广伟(2004) [2] 指出半方差风险有四种测度方法，分别是相对收益率、相对目标收益率、考虑资本因素的相对目标收益率和组合偏差风险的计量法，通过实证分析，发现考虑资本因素的相对收益率半方差风险计量法最优，并提出了半方差风险计量模型的改进方法。为了半方差模型能够更好地运用到实际投资中，有学者在半方差模型的基础上进行扩展，如张鹏和张忠桢(2008) [3] 分析了不允许卖空情况下的均值–半方差投资组合优化，并运用不等式组的旋转算法进行求解，孙全德和邓雪(2017) [4] 引入熵构建均值–半方差–熵模型，能够更好地考虑股票市场中的不确定因素，提高投资者投资行为的安全性，王春峰等(2002) [5] 、康志林(2014) [6] 、王晓琴和高岳林(2020) [7] 在投资组合是考虑了交易成本的影响，张鹏等(2016) [8] 对最小交易量进行了限制，张鹏和梁楚婷(2022) [9] 在投资组合模型中加入了上下界限制、交易成本和无风险资产借贷约束三种现实约束。

现有文献已经从多个方面对半方差模型进行了扩展，并应用在了实证中，但是考虑上半方差并通过实证进行检验的却比较少。参照卫海英和徐广伟(2004)的文章，在衡量风险时应当将收益率高于预期收益率的情况也考虑进去，收益率高于预期收益率的幅度越大，投资者面临的风险越小，使用上半方差对下半方差进行调整，即组合偏差的风险计量。本文将通过实证分析组合偏差风险计量中最优的上、下半方差比例，并使用最优比例的组合偏差风险计量与等比例投资、均值–方差模型、均值–下半方差模型进行对比分析，分析哪种投资组合能有更优的表现。

2. 投资组合模型

2.1. 均值–方差模型

Markowitz在1952年发表了《portfolio Selection》一文，首次将数理统计的方法应用到投资组合选择的研究中，很重要的一个概念就是用收益率的均值和方差来描述收益与风险。均值–方差模型需要一些基本假设，具体来说，有：

1) 每次资产组合分析都是在特定的单一时期进行；

2) 所有资产无限可分；

3) 资产收益率的均值和方差(或者标准差)是知道的，投资者以此作为投资决策的依据；

4) 市场是无摩擦的；

5) 投资者是理性的，厌恶风险的，因此在同样的收益率水平下会追求风险最小，在同样的风险水平下回追求收益率最大。

对于单个的风险资产，其收益率的表达式为：

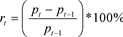(1)

其中， $r_t$ 表示风险资产在t期的收益率， $p_t$ 表示t时刻资产的价值。

使用资产收益率的均值和方差分别表示收益和风险，则在T时段内单个风险的收益和方差可以表示为：

$u=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{r}_t}$ (2)

${\sigma }^2=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left(r_t-u\right)}^2}$ (3)

其中， $u$ 表示收益率均值， ${\sigma }^2$ 表示收益率的方差。

两个风险资产的收益率的协方差的表达式为：

${\mathrm{cov}}_{i,j}=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(r_{i,t}-u_i\right)*\left(r_{j,t}-u_j\right)}$ (4)

其中， ${\mathrm{cov}}_{i,j}$ 表示风险资产i和风险资产j之间的协方差，可以看到， ${\text{cov}}_{i,i}$ 与 ${\sigma }_i^2$ 是一样的。

对有n个风险资产组合投资，使用组合收益率的均值和方差表示投资组合的收益和风险，则n个风险的投资组合的收益和风险可以表示为：

$u_p={\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i{u}_i}$ (5)

${\sigma }_p^2={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{x}_i{x}_j{\mathrm{cov}}_{i,j}}}$ (6)

其中， $u_p$ 表示投资组合的收益率均值， ${\sigma }_p^2$ 表示投资组合的收益率的方差， $x_i$ 表示第i个风险资产的投资比例。

因为投资者都是理性的，所以会在相同收益水平下追求风险最小，或者在相同风险水平下追求收益最大。本文以相同收益水平下追求风险最小为例，则均值–方差模型可以表示为：

$\begin{array}{l}\min {{\displaystyle }}^{}{\sigma }_p^2\\ s.t.\{\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}=1\\ u_p=u_m\\ x_i\ge 0,\left(i=1,2,3,\cdots ,n\right)\end{array}\end{array}$ (7)

其中， $u_m$ 表示预期收益率， $x_i\ge 0$ 说明不允许卖空。

2.2. 均值–下半方差模型

均值–方差模型使用收益率的方差来表示投资组合的风险，是存在一定的缺陷的。虽然风险被定义为收益率对预期收益率的偏离，但是在实际的投资中，只有收益率低于预期收益率才被叫做风险，而高于预期收益率被称为超额收益。因此，使用表示收益率向下偏离预期收益率的下半方差来代替方差衡量投资组合的风险，更为符合实际。

对于单个风险资产，令： $U^{-}=\max \left(0,u_m-u\right)=\{\begin{array}{l}0,u_m\le u\\ u_m-u,u_m>u\end{array}$ ，则下半方差可以表示为：

${\left({\sigma }^{-}\right)}^2={\left(U^{-}\right)}^2$ (8)

其中， ${\left({\sigma }^{-}\right)}^2$ 表示风险资产的下半方差。因为下半方差的协方差计算较为复杂，在衡量投资组合的下半方差时，本文选择将投资组合看作一个风险资产，先计算其收益率，然后根据收益率直接计算投资组合的下半方差，而不采用单个风险资产下半方差及下半方差协方差来计算投资组合的下半方差的方法。同样的选择相同收益率下追求风险最小的目标，均值–下半方差模型可表示为：

$\begin{array}{l}\min {{\displaystyle }}_{}{\left({\sigma }_p^{-}\right)}^2=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left\{\max \left(0,u_m-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i{u}_i}\right)\right\}}^2}\\ s.t.\{\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}=1\\ u_p=u_m\\ x_i\ge 0,\left(i=1,2,3,\cdots ,n\right)\end{array}\end{array}$ (9)

其中， ${\left({\sigma }_p^{-}\right)}^2$ 表示投资组合的下半方差。

2.3. 组合偏差模型

均值–下半方差模型对均值–方差进行了改进，但是针对上半方差却只是简单地省略，并没有有效地利用好上半方差。在实际的投资活动中，投资者对风险的预期会受到收益预期的影响，即预期收益越大，投资者能够承受的风险也越大，这与均值–方差模型的结论是一致的。因此，在使用组合偏差衡量投资组合的风险时，将表示超额收益的上半方差也考虑进去，更符合投资市场上投资者的实际心理。

同样的，对于单个风险资产，令： $U^{+}=\max \left(0,u-u_m\right)=\{\begin{array}{l}0,u\le u_m\\ u-u_m,u>u_m\end{array}$ ，则上半方差可以表示为：

${\left({\sigma }^{+}\right)}^2={\left(U^{+}\right)}^2$ (10)

其中， ${\left({\sigma }^{+}\right)}^2$ 表示风险资产的上半方差。

投资组合的上半方差可以表示为：

${\left({\sigma }_p^{+}\right)}^2=\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left\{\max \left(0,{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i{u}_i-u_m}\right)\right\}}^2}$ (11)

下半方差是收益率对预期收益率的向下偏差，衡量的是损失风险，上半方差是收益率对预期收益率的向上偏差，衡量的是超额收益。上半方差越大，超额收益的增加应当扩大投资者对投资组合损失风险的接受范围，因此投资组合的最终风险与上半方差是负向关系。组合偏差模型可以表示为：

$\begin{array}{l}\min {{\displaystyle }}_{}{\left({\sigma }_p^{-+}\right)}^2=\beta {\left({\sigma }_p^{-}\right)}^2-\left(1-\beta \right){\left({\sigma }_p^{+}\right)}^2\\ s.t.\{\begin{array}{l}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}=1\\ u_p=u_m\\ x_i\ge 0,\left(i=1,2,3,\cdots ,n\right)\end{array}\end{array}$ (12)

其中， $\beta$ 是一个不确定参数，取值在0到1之间，需要利用实际市场数据确定最优取值。

2.4. 投资组合累计收益率

本文中使用累计收益率作为衡量投资组合有效性的指标，所谓累计收益率，即将投资初期的资产设定为1，下一期的值为上一期末值与(1 + 上期收益率)的乘积。具体公式可表示为：

$R_t=R_{t-1}*\left(1+r_t\right)$ (13)

其中， $R_t$ 表示t期的累计收益率值， $r_t$ 表示t期的收益率。所以投资期末的累计收益率的计算公式为：

$R_T={\displaystyle \underset{t=1}{\overset{T}{\prod }}\left(1+r_t\right)}$ (14)

由计算公式可知，当期末的累计收益率值大于1时投资组合在投资期内获得收益，相反，期末的累计收益率值小于1则表示投资组合在投资期内出现亏损。

3. 实证分析

3.1. 数据选取

通过锐思金融数据库获取上证50指数成分股2021年和2022年每日收益率数据，剔除存在缺失值的股票，得到27支股票的日收益率数据。为减少各股票收益率之间的相关性，将27支取票2021年的日收益率均值进行排序，排序后选择收益率均值排名第1、第7、第14、第20和第27的5支股票作为进行资产组合分析的风险资产，分别为韦尔股份(603501)、万华化学(600309)、中国建筑(601668)、上汽集团(600104)和恒瑞医药(600276)。本文将根据2021年的收益率数据计算5支股票的投资比例，并根据2022年的收益率数据计算投资组合的收益情况，比较分析不同投资组合模型选出的投资组合的表现。

所选5支股票2021年和2022年日收益率数据的描述性统计如表1所示。

Table 1. Descriptive statistics of return rate data

表1. 收益率数据描述性统计

通过表1可知，与2021年相比，2022年股票的整体表现不佳，5支股票中有4支的收益率均值为负，由此可以初步预测各种投资组合方式最终的累计收益率均可能小于1，即在2022年投资期内出现亏损。

所选5支股票的相关系数如图1所示。

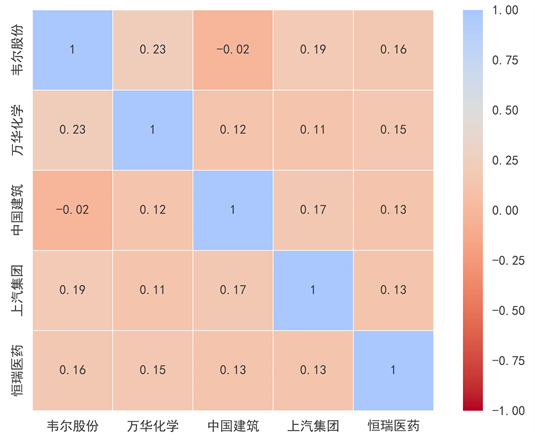
Figure 1. Stock correlation coefficient heatmap

图1. 股票相关系数热力图

从图1中可以看出，各股票之间最大的相关系数为0.23，说明不同股票的线性相关性较低，可以使用投资组合的方式分散投资风险，所选股票适合本文的分析使用。

3.2. 等比例投资

使用投资组合模型计算投资比例前，使用简单的等比例投资，观察等比例投资的表现，将等比例投资用作参考。等比例投资的累计收益率表现如图2所示。

图2中蓝色的“EW”表示等比例投资的累计收益率曲线，可以看到，在等比例投资的情况下，2022年末最终是亏损的状态。可能是受行情不佳的影响，等比例投资的期末累计收益率值约为0.75，2022全年累计亏损约25%。

3.3. 均值–方差模型

设定年化的预期收益率 $u_m=10\%$ ，在此收益率条件下追求由方差表示的风险最小。按照模型(7)的表达式，根据2021年的收益率数据，利用Python进行求解，得到各股票的投资比例，并使用2022年的收益率数据进行回测。均值–方差模型的投资组合2022年回测表现如图3所示。

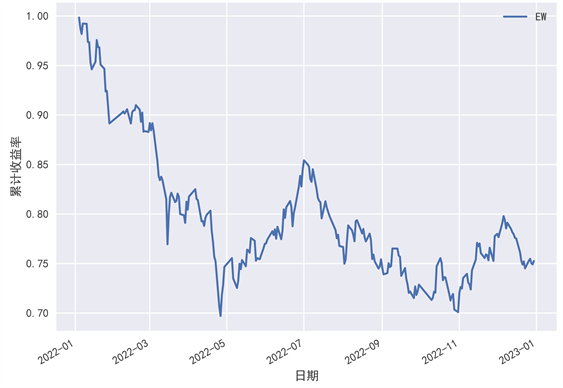
Figure 2. Equal proportion investment cumulative return chart

图2. 等比例投资累计收益图

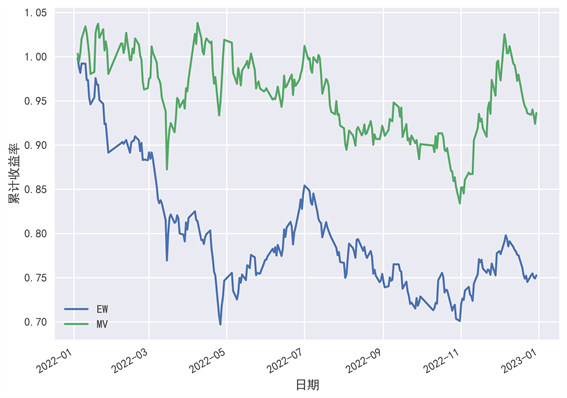
Figure 3. Mean variance model investment portfolio cumulative return chart

图3. 均值–方差模型投资组合累计收益图

图3中，绿色的“MV”线表示均值–方差投资组合的累计收益率。通过图3可以看到，均值–方差模型选出的投资组合整体表现是明显优于等比例投资的，虽然期末累计收益率值仍然小于1，存在亏损，但是累计收益率在整个投资期内一直高于等比例投资的累计收益率。

3.4. 均值–下半方差模型

同样的，将预期收益率定为10%，在预期收益率下追求由下半方差表示的风险最小。因为下半方差的协方差矩阵计算较为复杂，所以本文选择将投资组合看作一个风险资产的方式，先计算投资组合的日收益率，再根据日收益率数据计算投资组合的下半方差。按照模型(9)的表达式，根据2021年的收益率数据，利用Python进行求解，得到各股票的投资比例并分析2022年回测表现。均值–下半方差模型的投资组合2022年回测表现如图4所示。

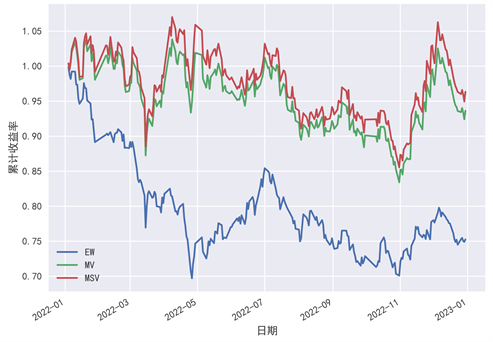
Figure 4. Mean lower half variance portfolio cumulative return chart

图4. 均值–下半方差投资组合累计收益图

图4中，红色的“MSV”线表示由均值–下半方差模型选出的投资组合的累计收益率。从图4可以看出，均值–下半方差模型选出的投资组合，在投资期内的累计收益率优于均值–方差模型，说明均值–下半方差模型能够选出更为合理的投资组合，帮助投资者在一定的预期收益率水平下控制风险。

3.5. 组合偏差模型

均值–下半方差模型使用收益率的下半方差衡量投资组合的风险，但是忽略了收益率的上半方差，组合偏差模型就是将投资组合的上半方差也考虑进来，用超额收益调整投资者对损失风险的接受范围。简单来说，对于下半方差相同的风险资产，会认为上半方差大的更有投资价值。组合偏差模型需要先确定一个最优的参数 $\beta$ ，按照模型(12)的表达式，将2021年的股票日收益率数据分为两部分，使用2021年的股票日收益率数据的前半部分对模型进行求解，然后利用后半部分的数据进行回测以确定最优参数。本文对 $\beta$ 分别取值为0.1到0.9，每次增加0.1，然后根据不同 $\beta$ 值的投资组合的表现，确定最优的参数。不同参数取值的累计收益率情况如图5所示。

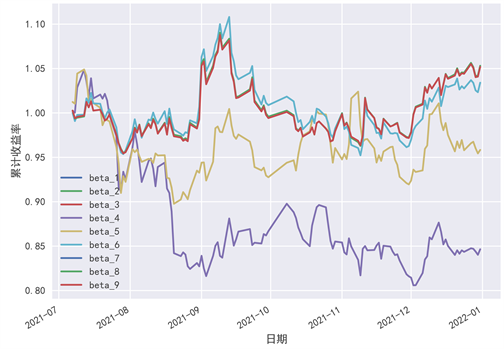
Figure 5. Cumulative yield chart of investment portfolio with different parameter combination bias

图5. 不同参数的组合偏差投资组合累计收益率图

图5中名为“beta_i”的线表示的是参数 $\beta =i/10$ 的组合偏差模型投资组合的累计收益率。从图中可以看出，当参数 $\beta =0.8$ 时，投资组合的表现最好，即最佳参数为0.8。

将参数定为0.8，绘制组合偏差模型投资组合的累计收益率图，结果如图6所示。

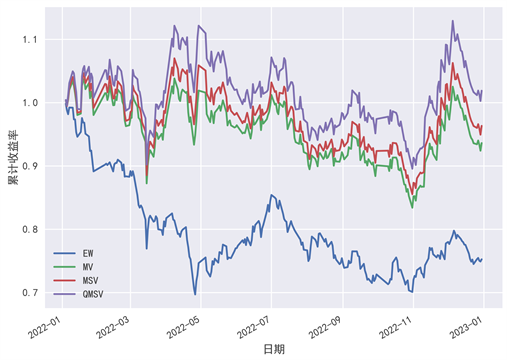
Figure 6. Combination deviation model investment portfolio cumulative yield chart

图6. 组合偏差模型投资组合累计收益率图

图6中，紫色的“QMSV”线表示组合偏差模型选出的投资组合的累计收益率。从图中可以看到，组合偏差的投资组合表现是所有投资组合中表现最好的，相比于均值–下半方差模型的投资组合，组合偏差投资组合的累计收益率曲线始终在均值–下半方差投资组合的上方，且从投资期末看，组合偏差模型的投资组合是唯一一个期末累计收益率值大于1，即收益为正的投资组合。说明采用组合偏差模型的方式衡量风险更符合投资市场的实际情况，能够选择出更加合理的投资组合。

4. 研究结论

本文介绍了均值–方差模型、均值–下半方差模型和组合偏差模型后，在上证50指数的成分股中选取了5支股票作为样本，将2021年的日收益率数据当作训练数据，2022年的日收益率数据作为回测数据，分别构建等比例投资组合、均值–方差模型投资组合、均值–下半方差模型投资组合和组合偏差模型投资组合，根据回测的结果分析各投资组合的表现。得到的主要结论如下：

1) 从投资组合的表现来看，组合偏差 > 均值–下半方差 > 均值–方差 > 等比例投资。在对模型进行求解时，文中设定了预期年化收益率为10%，求解出风险最小的投资组合，然后用2022年的日收益率数据对投资组合进行回测。从回测的累计收益率来看，等比例投资获得的收益率是最低的，组合偏差投资组合获得的收益率最高，均值–方差模型和均值–下半方差模型投资组合的收益率位于中间，且二者获得的收益率相差不大，不过仍能看出均值–下半方差模型的投资组合稍优于均值–方差模型的投资组合。

2) 衡量投资组合的风险时应当将超额收益的因素考虑进去。均值–方差模型、均值–下半方差模型和组合偏差模型的不同主要在于对风险的衡量方式。均值–方差模型将投资组合的方差看作风险；但是人们投资时更看重收益率低于预期收益率的损失风险，因此均值–下半方差将投资组合的下半方差看作投资组合的风险，能够得到更加合理的投资组合；不过均值–下半方差模型忽略了上半方差的作用，上半方差代表的超额收益应当对投资组合的风险有调节作用，因此组合偏差模型使用上、下半方差的组合来衡量投资组合的风险，更加符合真实的投资市场情况，能够得出更可信的投资组合。从回测的结果来看，组合偏差模型的投资组合确实能获得更大的收益，因此衡量投资组合风险是要考虑超额收益的因素。

3) 衡量投资组合风险时下半方差是主要的因素。文中得出的组合偏差模型的最优参数是0.8，即投资组合的风险中下半方差的权重是80%，大于上半方差的20%，说明衡量风险是应当以下半方差为主要因素，上半方差能够调节风险，但影响力度低于下半方差，说明不能够单独考虑收益或单独考虑风险，应当将二者结合起来，才能做出更合理的投资决策。