基于BP神经网络的自适应模糊半参数时间序列模型

Adaptive Fuzzy Semiparametric Time Series Model Based on BP Neural Network

摘要: 本文介绍了一种自适应模糊半参数时间序列模型，该模型将半参数技术与反向传播神经网络(BPNN)相结合，形成具有LR-型模糊数据的自适应模糊时间序列模型。首先，提出了基于非参数核、加权最小二乘和交叉验证的混合方法，该方法可以同时估计回归参数和光滑函数以及带宽的最优值；其次，基于非线性残差序列建立BP神经网络，通过神经网络的运算得到新的偏差，使得在不确定条件下获得更丰富的信息，提高了预测精度。本文采用一些常见的拟合优度准则来检验所提出的自适应模糊半参数时间序列模型的性能。通过一个模拟仿真的例子，说明了该方法的有效性。最后，对所得结果的统计分析表明，该模型对模糊时间序列数据的预测具有可靠性和有效性，优于其他模糊时间序列预测模型。

Abstract: In this paper we introduce a fuzzy semiparametric time series model aggregating semiparametric techniques and neural network into adaptive fuzzy time series model with LR-type fuzzy data. First, a hybrid approach including nonparametric kernel-based method, weighted least squares and cross-validation method is suggested, which could simultaneously estimate both regression param-eters and smooth function of the innovations along with optimal value of the bandwidth. Next, back propagation neural network (BPNN) is created based on the nonlinear residual sequence and then new deviations are attained as a result of operating with neural network, so that the richer infor-mation can be obtained under uncertain conditions and the prediction accuracy is improved. Some common goodness-of-fit criteria are employed to examine the performance of the proposed adap-tive fuzzy semiparametric time series model. A simulation example is given to illustrate the effec-tiveness of this method. Last, statistical analyses of obtained results indicate that the proposed model is reliable and effective for predicting fuzzy time series data and superior to other fuzzy time series forecasting models.

1. 引言

时间序列预测是基于过去时间序列值对数据集进行建模，这些数据集用于预测未来值。时间序列预测方法在商业、金融、计算机科学、工程、医学、物理、化学等许多跨学科领域都有广泛的应用。经典的时间序列分析评估在很大程度上是基于精确的信息。然而，在现实世界中，关于底层系统的一些信息可能是不精确的，并且以模糊量的形式表示。因此，有必要将经典方法推广到模糊环境中来研究和分析利益系统。对于这种情况，模糊时间序列模型在过去几十年中由于其在统计学和工程学中的广泛应用而获得了相当大的关注，例如招生 [1] ，股票指数价格 [2] ，温度 [3] ，财务预测 [4] 和农产品 [5] 等。

Song and Chissom [6] 最早提出了模糊时间序列的概念，并针对精确数据给出了模糊时间序列模型求解方法。模糊时间序列模型的求解主要由模糊化、模糊关系的建立和去模糊化等步骤组成。模糊逻辑关系的识别技术是求解模糊时间序列模型的重要一环，引起了许多研究者的兴趣，并得到了广泛的研究。模糊逻辑关系识别技术主要包括模糊逻辑关系群和模糊逻辑关系矩阵 [7] 、软计算技术 [8] 以及采用模糊逻辑的统计技术等 [9] 。

在许多实际问题中，模糊时间序列数据之间除了具有线性关系，一般还具有非线性关系。神经网络作为非线性映射的逼近器具有很高的能力 [10] 。因此，许多研究人员将神经网络与模糊时间序列结合起来，以达到更好的预测效果。Huarng和Yu [8] 提出了一种混合模型，结合反向传播神经网络与简单方法，实现了已知模式与未知模式分开预测，提高了预测精度。Khashei et al. [11] 将人工神经网络和模糊回归模型结合，提出了一种新的混合模型用于不完全数据条件下的时间序列预测。Egrioglu et al. [12] 提出了一种新的混合模糊时间序列方法，利用模糊c均值(FCM)方法和人工神经网络分别进行模糊化和去模糊化。Gu et al. [13] 提出了一种将信息颗粒划分方法与反向传播神经网络(BPNN)相结合的时间序列预测模型。

非参数技术在模糊时间序列预测中也被广泛应用。Hesamian和Akbari [14] 提出并讨论了一种基于非参数核的统计方法，对LR-型模糊时间序列数据进行了预测。然而，作为一种完全非参数的方法，它通常会导致一些缺点，如维数诅咒、解释困难和缺乏外推能力。模糊半参数回归模型通常比相应的模糊非参数回归模型更具优势和灵活性。Hesamian和Akbari [15] 提出了一个具有模糊数据、非模糊系数和模糊平滑函数的半参数时间序列模型。Zarei et al. [16] 对Hesamian和Akbari [15] 模型进行了拓展，对模糊数据采用了不同的距离度量。

本文结合非参数核方法、加权最小二乘法和BP神经网络，引入了基于BP神经网络的自适应模糊半参数时间序列模型。本文使用了半参数统计推断和加权最小二乘法，与使用最小二乘法的参数和非参数方法相比，通常会产生稳健性和灵活性的结果。此外，在不确定条件下，BP神经网络可以获得更丰富的信息和更高的预测精度。然后通过比较一些常见的拟合优度标准的结果来检验所提出方法的有效性和优点。为了进行比较研究，将所提出的模型与现有的一些模糊时间序列模型进行了仿真例子的比较。数值和比较结果表明，所提出的模型可以在模糊时间序列分析中提供足够准确的结果，并且可以抵消估计过程中可能出现的模糊异常值的破坏性影响。

本文的其余部分组织如下：第2节回顾了模糊数和模糊时间序列、模糊自回归分布滞后模型和模糊半参数时间序列模型的基本概念，这些概念对本文提出的方法至关重要。在第3节中，提出了一种基于BP神经网络的自适应模糊半参数时间序列模型。然后，给出了本文提出的迭代算法步骤，同时介绍了一些常见的拟合指标，来评估所提出模型的拟合效果。第4节利用模拟仿真的例子进行了一些比较研究，以验证所提出模型的可行性和有效性，并在最后一节给出了一些结论。

2. 预备知识

在本节中，我们将介绍模糊数和模糊时间序列、模糊自回归分布滞后模型、模糊半参数时间序列模型的基本概念。

2.1. 模糊数和模糊时间序列

给定论域 $ℝ$ ，模糊集 $\tilde{A}$ 由其隶属函数 ${\mu }_{\tilde{A}}\left(x\right):ℝ\to \left[0,1\right]$ 定义，对于 $\alpha \in \left[0,1\right]$ ， $\left\{x\in ℝ|\tilde{A}\left(x\right)\ge \alpha \right\}$ 称为模糊集 $\tilde{A}$ 的 $\alpha$ -水平集，并记作 $A\left[\alpha \right]$ ，区间表示为 $\tilde{A}\left[\alpha \right]=\left[{\tilde{A}}_{\alpha }^L,{\tilde{A}}_{\alpha }^U\right]$ ，其中， ${\tilde{A}}_{\alpha }^L=inf\left\{x:x\in \tilde{A}\left[\alpha \right]\right\}$ ， ${\tilde{A}}_{\alpha }^U=sup\left\{x:x\in \tilde{A}\left[\alpha \right]\right\}$ 。如果对于 $\forall \alpha \in \left[0,1\right]$ ， $A\left[\alpha \right]$ 是有限闭区间，则实数域 $ℝ$ 上的模糊集 $\tilde{A}$ 称为 $ℝ$ 上的一个模糊数 [17] 。

定义1 [17] LR-型模糊数 $\tilde{A}$ 由其隶属函数定义，通常表示为 $\tilde{A}={\left(a;l_a,r_a\right)}_{LR}$ ：

${\mu }_{\tilde{A}}\left(x\right)=\{\begin{array}{cc}L\left(\frac{a-x}{l_a}\right),& x\le a,\\ R\left(\frac{x-a}{u_a}\right),& x>a.\end{array}$ (1)

由上式可知，LR-型模糊数由中心值 $a\in ℝ$ ，左展形和右展形 $l_a,u_a\in {ℝ}^{+}$ ，严格递减的形状函数 $L,R:{ℝ}^{+}\to \left[0,1\right]$ ，且 $L\left(0\right)=R\left(0\right)=1$ 组成。当 $l_a=u_a=0$ 时，LR型模糊数退化为清晰值 $a$ 。

当 $L=R$ 且 $l_a=u_a=s$ 时，LR-型模糊数为对称模糊数，记为 $\tilde{A}={\left(a;s\right)}_L$ 。当形状函数 $L\left(x\right)=R\left(x\right)=\max \left\{0,1-x\right\}$ 时，LR-型模糊数为三角模糊数，记作 $\tilde{A}={\left(a;l_a,u_a\right)}_T$ ，若 $l_a=u_a=s$ ，LR-型模糊数为对称三角模糊数，记作 $\tilde{A}={\left(a;s\right)}_T$ 。

定义2 [1] 设 $ℝ$ 的子集 $Y\left(t\right)\left(t=\cdots ,0,1,2,\cdots \right)$ 是定义在模糊集 $f_j\left(t\right)\left(j=1,2,\cdots \right)$ 的论域， $F\left(t\right)$ 是 $f_j\left(t\right)\left(j=1,2,\cdots \right)$ 的集合，则 $F\left(t\right)$ 称为 $Y\left(t\right)\left(t=\cdots ,0,1,2,\cdots \right)$ 上的模糊时间序列。

定义3 [18] 假设 $\tilde{A}={\left(a;l_a,u_a\right)}_{LR}$ 和 $\tilde{B}={\left(b;l_b,u_b\right)}_{LR}$ 是LR-型模糊数，则 $\tilde{A}$ 与 $\tilde{B}$ 之间偏差平方距离定义如下：

$d^2\left(\tilde{A},\tilde{B}\right)={\left(a-b\right)}^2+{\left\{\left(a-L{l}_a\right)-\left(b-L{l}_b\right)\right\}}^2+{\left\{\left(a+R{u}_a\right)-\left(b+R{u}_b\right)\right\}}^2,$ (2)

其中， $L={\displaystyle {\int }_0^1{L}^{-1}\left(w\right)\text{d}w,}R={\displaystyle {\int }_0^1{R}^{-1}\left(w\right)\text{d}w}$ 。

当 $\tilde{A}$ 和 $\tilde{B}$ 是对称模糊数时，即 $L=R$ 且 $l_a=u_a=s_a$ ， $l_b=u_b=s_b$ ，距离定义为：

$d^2\left(\tilde{A},\tilde{B}\right)=3{\left(a-b\right)}^2+2L^2{\left(s_a-s_b\right)}^2,$ (3)

特别地，当 $\tilde{A}$ 和 $\tilde{B}$ 是对称三角模糊数时，即 $L=R=\frac{1}{2}$ ，距离定义为：

$d^2\left(\tilde{A},\tilde{B}\right)=3{\left(a-b\right)}^2+\frac{1}{2}{\left(s_a-s_b\right)}^2.$ (4)

2.2. 模糊自回归分布滞后模型

考虑模糊时间序列 ${\tilde{Y}}_t\left(t=1,2,\cdots \right)$ ， $X_k\left(k=1,2,\cdots \right)$ ，其中 ${\tilde{Y}}_t$ 是响应变量， $X_k$ 是解释变量，那么模糊自回归分布滞后模型具体如下 [19] ：

${\tilde{Y}}_t={\tilde{A}}_0+{\tilde{A}}_{1}t+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\tilde{\theta }}_i{Y}_{t-i}}+{\displaystyle \underset{j=1}{\overset{k}{\sum }}{\displaystyle \underset{I_j=0}{\overset{q_j}{\sum }}}}{\tilde{\beta }}_{j,I_j}{X}_{j,t-I_j}+{\tilde{\epsilon }}_t=\tilde{A}{Y}_t^{*}+{\tilde{\epsilon }}_t.$ (5)

其中， $Y_t^{*}={\left[1t{Y}_{t-i}{X}_{j,t-I_j}\right]}^{\prime }$ 是自变量向量， $Y_{t-i}$ 是 $Y_t$ 滞后 $i$ 阶的值， $\tilde{A}={\left[{\tilde{A}}_0{\tilde{A}}_1{\tilde{\theta }}_i{\tilde{\beta }}_{j,I_j}\right]}^{\prime }$ 是未知模糊系数向量，表示为对称三角模糊数，记作 $\tilde{A}={\left(\alpha ,c\right)}_T$ ，其中 $\alpha$ 为中心值， $c$ 为展形， ${\tilde{\epsilon }}_t$ 是随机模糊误差项。

2.3. 模糊半参数时间序列模型

考虑模糊时间序列 ${\tilde{Y}}_t\left(t=1,2,\cdots \right)$ ，则模糊半参数时间序列模型具体如下 [15] ：

${\tilde{Y}}_t={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\theta }_i}{\tilde{Y}}_{t-i}+\tilde{f}\left({\tau }_t\right)+{\tilde{\epsilon }}_t,t=p+1,p+2,\cdots ,T.$ (6)

其中， ${\theta }_i\left(i=1,2,\cdots ,p\right)$ 是待估计的实值系数， ${\tilde{Y}}_{t-i}$ 是 ${\tilde{Y}}_t$ 滞后 $i$ 阶的值， $\tilde{f}\left({\tau }_t\right)={\left(f\left({\tau }_t\right);l_{f({\tau }_t)},r_{f({\tau }_t)}\right)}_{LR}$ 是未知的模糊光滑函数，且 $l_{f({\tau }_t)},r_{f({\tau }_t)}\ge 0$ ， ${\tau }_t=\frac{t}{T}$ 是协变量， ${\tilde{\epsilon }}_t={\left({\epsilon }_t;l_{{\epsilon }_t},r_{{\epsilon }_t}\right)}_{LR}$ 是随机模糊误差。

3. 建立模型

在本节中，我们结合神经网络和半参技术提出了自适应模糊时间序列模型，并给出了模型的算法步骤和拟合指标。

3.1. 基于BPNN的自适应模糊半参数时间序列模型

考虑一组模糊时间序列数据 ${\tilde{r}}_t\left(t=1,2,\cdots ,T\right)$ ，其中 ${\tilde{r}}_t={\left(c_t;l_t,u_t\right)}_{LR}$ 。我们考虑以下自适应模糊半参数时间序列模型：

$\{\begin{array}{l}{c}_t={\alpha }_1{c}_{t-1}+{\alpha }_2{c}_{t-2}+\cdots +{\alpha }_p{c}_{t-p}+f\left({\tau }_t\right)+{\epsilon }_{c,t},\hfill \\ l_t={\beta }_0+{\beta }_1{l}_{t-1}+{\beta }_2{l}_{t-2}+\cdots +{\beta }_q{l}_{t-q}+{\gamma }_1{\hat{c}}_t+{\epsilon }_{l,t},\hfill \\ u_t={\phi }_0+{\phi }_1{r}_{t-1}+{\phi }_2{r}_{t-2}+\cdots +{\phi }_m{r}_{t-m}+{\gamma }_2{\hat{c}}_t+{\epsilon }_{u,t},t=k+1,\cdots ,T\hfill \end{array}$ (7)

其中， $k=\max \left(p,q,m\right),{\alpha }_1,\cdots ,{\alpha }_p,{\beta }_0,{\beta }_1,\cdots ,{\beta }_q,{\gamma }_1,{\phi }_0,{\phi }_1,\cdots ,{\phi }_m,{\gamma }_2$ 是模型中的未知实值系数， ${\epsilon }_{c,t},{\epsilon }_{l,t},{\epsilon }_{u,t}$ 分别是中心，左展形，右展形的随机误差， ${\hat{c}}_t$ 是 $c_t$ 的估计值， $f\left({\tau }_t\right)$ 是未知的光滑函数， ${\tau }_t=\frac{t}{T}$ 是协变量。该模型基于三个子模型。第一个子模型结合非参，考虑了中心和其滞后阶之间的线性关系和标量 $t$ 之间的非线性关系，其他两个子模型在第一个模型的基础上分别考虑了左展形和右展形与其滞后阶和中心估计值 ${\hat{c}}_t$ 之间的线性关系。

根据Wang et al. [20] ，我们可以估计未知的光滑函数 $\hat{f}\left({\tau }_t\right)$ ：

$\hat{f}\left({\tau }_t\right)={\displaystyle \underset{j=k+1}{\overset{T}{\sum }}{w}_j}\left({\tau }_t\right)\left(c_j-{\displaystyle \underset{l=1}{\overset{p}{\sum }}{\alpha }_l}{c}_{j-p}\right),$ (8)

其中， $w_j\left({\tau }_t\right)=\frac{\frac{1}{Th}K\left(\frac{{\tau }_j-{\tau }_t}{h}\right)}{\frac{1}{Th}{\displaystyle \underset{j=k+1}{\overset{T}{\sum }}K}\left(\frac{{\tau }_j-{\tau }_t}{h}\right)},$ 且 $h>0$ 为核函数 $K(\cdot )$ 的带宽。

将(6)式代入(5)对应的第一个子模型中，得到中心，左展形和右展形的估计值，记作 ${\widehat{\stackrel{˜}{r}}}_t={\left({\hat{c}}_t;{\hat{l}}_t,{\hat{u}}_t\right)}_{LR}$ ：

$\{\begin{array}{l}{\hat{c}}_t={\displaystyle \underset{j=k+1}{\overset{T}{\sum }}{w}_j}\left({\tau }_t\right)c_j+{\displaystyle \underset{l=1}{\overset{p}{\sum }}{\alpha }_l}\left(c_{t-l}-{\displaystyle \underset{j=k+1}{\overset{T}{\sum }}{w}_j}\left({\tau }_t\right)c_{j-l}\right),\hfill \\ {\hat{l}}_t={\beta }_0+{\beta }_1{l}_{t-1}+{\beta }_2{l}_{t-2}+\cdots +{\beta }_q{l}_{t-q}+{\gamma }_1{\hat{c}}_t,\hfill \\ {\hat{u}}_t={\phi }_0+{\phi }_1{u}_{t-1}+{\phi }_2{u}_{t-2}+\cdots +{\phi }_m{u}_{t-m}+{\gamma }_2{\hat{c}}_t,t=k+1,\cdots ,T\hfill \end{array}$ (9)

其次，采用加权最小二乘法，我们可以估计未知的实值系数 $\alpha =\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_p\right),$ $\beta =\left({\beta }_0,{\beta }_1,{\beta }_2,\cdots ,{\beta }_q\right),$ $\phi =\left({\phi }_0,{\phi }_1,{\phi }_2,\cdots ,{\phi }_m\right),$ $\gamma =\left({\gamma }_1,{\gamma }_2\right)$，具体如下：

$\left(\hat{\alpha },\hat{\beta },\hat{\phi },\hat{\gamma }\right)=\underset{\alpha \in {ℝ}^p,\beta \in {ℝ}^q,\phi \in {ℝ}^m,\gamma \in {ℝ}^2}{argmin}{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{w}_t}{d}^2\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t\right)$ (10)

其中， $d^2\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t\right)$ 是 ${\widehat{\stackrel{˜}{r}}}_t$ 和 ${\tilde{r}}_t$ 之间偏差平方距离， $w_t=\frac{1}{1+d^2\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t\right)}$ 是第t个残差对应的权重，残差越大的时间序列数据，权重越小，这样可以减弱异常数据对模型的干扰。

实际的模糊时间序列数据除了具有线性特征，还一般具有非线性特征。神经网络模型具有较强的学习能力和数据处理能力，能够挖掘数据背后复杂的甚至难用数学形式描述的非线性关系 [10] 。神经网络模型种类很多，其中基于误差反向传播算法的多层前馈神经网络，即BP神经网络，是应用最广的一种神经网络模型。

因此，本文针对残差序列中隐含的原始序列中的非线性关系，考虑了一个三层BP神经网络来逼近这种非线性关系，其中包含输入层，隐藏层，和输出层。假设BP神经网络有n个输入，则这个残差序列关系可写成：

$\{\begin{array}{l}{\epsilon }_t=f\left({\epsilon }_{t-1},{\epsilon }_{{\epsilon }_{t-2}},\cdots ,{\epsilon }_{t-n}\right)+{\epsilon }_t^{*},\hfill \\ {\epsilon }_{l,t}=g\left({\epsilon }_{l,t-1},{\epsilon }_{l,t-2},\cdots ,{\epsilon }_{l,t-n}\right)+{\epsilon }_{l,t}^{*},\hfill \\ {\epsilon }_{u,t}=h\left({\epsilon }_{u,t-1},{\epsilon }_{u,t-2},\cdots ,{\epsilon }_{u,t-n}\right)+{\epsilon }_{u,t}^{*}.\hfill \end{array}$ (11)

其中， ${\epsilon }_t=c_t-{\hat{c}}_t$ ， ${\epsilon }_{l,t}=l_t-{\hat{l}}_t$ ， ${\epsilon }_{u,t}=u_t-{\hat{u}}_t$ 分别是自适应模糊半参数时间序列预测模型得到的中心、左展形和右展形的残差， $f$ ， $g$ ， $h$ 是由神经网络决定的非线性函数，一般为logistic函数，即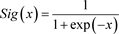， ${\epsilon }_t^{*}$ ， ${\epsilon }_{l,t}^{*}$ 和 ${\epsilon }_{u,t}^{*}$ 分别是中心、左展形和右展形的随机误差。BP神经网络具体结构如图1所示：

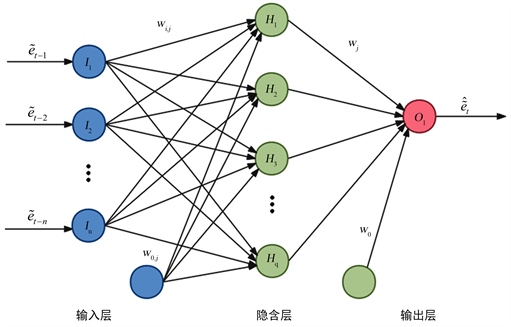
Figure 1. Structure of three-layer BP neural network

图1. 三层BP神经网络结构

通过BP神经网络估计的中心、左展形和右展形的残差 ${\epsilon }_t$ ， ${\epsilon }_{l,t}$ 和 ${\epsilon }_{u,t}$ 预测值分别记为 ${\hat{\epsilon }}_t^{NN}$ ， ${\hat{\epsilon }}_{l,t}^{NN}$ 和 ${\hat{\epsilon }}_{u,t}^{NN}$ ，那么将基于半参技术和加权最小二乘的结果 ${\widehat{\stackrel{˜}{r}}}_t={\left({\hat{c}}_t;{\hat{l}}_t,{\hat{u}}_t\right)}_{LR}$ 与BP神经网络所得残差估计值结合，则可以得到基于BP神经网络的自适应模糊半参数时间序列模型的最终估计值 ${\widehat{\stackrel{˜}{r}}}_t^{*}={\left({\hat{c}}_t^{*};{\hat{l}}_t^{*},{\hat{u}}_t^{*}\right)}_{LR}$ ：

$\{\begin{array}{l}{\hat{c}}_t^{*}={\hat{c}}_t+{\hat{\epsilon }}_t^{NN},\hfill \\ {\hat{l}}_t^{*}={\hat{l}}_t+{\hat{\epsilon }}_{l,t}^{NN},\hfill \\ {\hat{u}}_t^{*}={\hat{u}}_t+{\hat{\epsilon }}_{u,t}^{NN},t=k+n+1,\cdots ,T\hfill \end{array}$ (12)

3.2. 估计未知参数的算法

为了估计模型中的未知系数和未知光滑函数，本文提出了以下迭代算法过程：

步骤1：选择一个核函数，选择一个滞后阶数 $p\in \left\{1,2,\cdots ,P\right\},P\in \mathbb{N}$ ， $q\in \left\{1,2,\cdots ,Q\right\},Q\in \mathbb{N}$ ， $m\in \left\{1,2,\cdots ,M\right\},M\in \mathbb{N}$ ，其中，中心，左展形和右展形的滞后阶数的上限由样本自相关系数决定；

步骤2：假定初始带宽 $h_{(0)}=0.01$ ；

步骤3：利用初始带宽 $h_{(0)}$ 和式(8)计算此时未知系数 ${\alpha }_{h(0)},{\beta }_{h(0)},{\phi }_{(0)},{\gamma }_{h(0)}$ ；

步骤4：计算CV值，当CV值达到下确界时，此时 $h_{(0)}$ 即为最优带宽 $h_{opt}$ ，否则，令 $h_{(1)}=h_{(0)}+0.01$ ，回到步骤3，重复以上步骤；

$CV\left(h_{(0)}\right)=\frac{1}{T-k}{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{d}^2}\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t^{h_{(0)}}\right),$ (13)

其中， ${\widehat{\stackrel{˜}{r}}}_t{}^{h_{(0)}}$ 是中心，左展形和右展形滞后阶数为 $p,q,m$ ，带宽为 $h_{(0)}$ 时的 ${\tilde{r}}_t$ 的估计值。

步骤5：计算自适应模糊半参数时间序列模型的残差 ${\tilde{e}}_t={\left(e_t;l_{e_t},r_{e_t}\right)}_{LR}$ ，然后基于BP神经网络得到 ${\widehat{\stackrel{˜}{e}}}_t={\left({\hat{e}}_t;{\hat{l}}_{e_t},{\hat{r}}_{e_t}\right)}_{LR}$ ，并根据式(12)计算得出 ${\widehat{\stackrel{˜}{r}}}_t^{*}={\left({\hat{c}}_t^{*};{\hat{l}}_t^{*},{\hat{r}}_t^{*}\right)}_{LR}$ ；

步骤6：选择另一组滞后阶数 $p,q,m$ ，其中 $p\in \left\{1,2,\cdots ,P\right\},q\in \left\{1,2,\cdots ,Q\right\},m\in \left\{1,2,\cdots ,M\right\},$ 其中 $P\in \mathbb{N},$ $Q\in \mathbb{N}$ 且 $M\in \mathbb{N}$ 回到步骤2，并重复以上步骤，模型的拟合优度达到最大时就得了最优的系数估计值。

3.3. 模型评价

本文采用以下三个拟合指标来评价模糊时间序列模型的性能 [21] [22] ：

$G_1=\frac{{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}\frac{1}{1+E_1\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)}}}{T-k}$ (14)

其中， $E_1\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)={\displaystyle \int \frac{\left|{\widehat{\stackrel{˜}{r}}}_t\left(x\right)-{\tilde{r}}_t\left(x\right)\right|}{{\displaystyle \int {\tilde{r}}_t}\left(x\right)\text{d}x}\text{d}x}$ ， $G_1$ 越大，说明模糊时间序列模型的观测值与估计值越接近。

$MD=\frac{{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{E}_2}\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)}{T-k}$ (15)

其中， $E_2\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)=\frac{1}{2z}{\displaystyle \underset{j=1}{\overset{z}{\sum }}\left(\left|{\widehat{\stackrel{˜}{r}}}_t^L\left[{\alpha }_j\right]-{\tilde{r}}_t^L\left[{\alpha }_j\right]\right|+\left|{\widehat{\stackrel{˜}{r}}}_t^U\left[{\alpha }_j\right]-{\tilde{r}}_t^U\left[{\alpha }_j\right]\right|\right)}$ ， ${\alpha }_1<\cdots <{\alpha }_z$ 是[0, 1]的任意分区， ${\widehat{\stackrel{˜}{r}}}_t^L\left[{\alpha }_j\right]$ 和 ${\widehat{\stackrel{˜}{r}}}_t^U\left[{\alpha }_j\right]$ 是 ${\widehat{\stackrel{˜}{r}}}_t$ 的 $\alpha$ -水平截集的左端点和右端点。MD越大，说明模糊时间序列模型的观测值与估计值的拟合效果越差。

$S\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)=\frac{1}{T-k}{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{S}_{UI}}\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)$ (16)

其中， $S_{UI}\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)=\frac{Card\left({\widehat{\stackrel{˜}{r}}}_t\cap {\tilde{r}}_t\right)}{Card\left({\widehat{\stackrel{˜}{r}}}_t\cup {\tilde{r}}_t\right)}$ ， $\cap$ 和 $\cup$ 分别表示模糊数空间中的交集算子和并算子， $Card\left(\tilde{A}\right)$ 表示 $\tilde{A}$ 的基数。贴近度S越大，说明模糊时间序列模型的观测值与估计值更接近，模型拟合效果越好。

4. 实证分析

在本节中，我们通过模拟仿真的例子来验证本文模型的可行性和有效性。考虑以下自适应模糊半参数时间序列模型生成的模拟模糊数据集样本，样本量为100：

$\{\begin{array}{l}{c}_t=0.6c_{t-1}+f\left({\tau }_t\right)+{\epsilon }_{c,t},\hfill \\ l_t=0.3+0.4l_{t-1}-0.08{\hat{c}}_t+{\epsilon }_{l,t},\hfill \\ u_t=0.2+0.6u_{t-1}-0.1{\hat{c}}_t+{\epsilon }_{u,t},t=2,3,\cdots ,100\hfill \end{array}$ (17)

其中， $c_1$ ， $l_1$ 和 $u_1$ 分别是中心、左展形和右展形的初始值，并且 $c_1~N\left(0,9\right)$ ， $l_1$ 和 $u_1$ 是来自 $U\left(0,2\right)$ 的随机样本，误差项 ${\epsilon }_{c,t}~N\left(0,0.1\right)$ ， ${\epsilon }_{l,t}$ 和 ${\epsilon }_{u,t}$ 是来自 $U\left(0,0.01\right)$ 的随机样本，光滑函数 $f\left({\tau }_t\right)=\sqrt{{\tau }_t\left(1-{\tau }_t\right)}\sin \left(\frac{0.2\pi }{{\tau }_t+0.05}\right)$ ，其中 ${\tau }_t=\frac{t}{100},t=2,3,\cdots ,100$ 。

为了排除偶然性，我们将模型(18)拟合了1000次，以验证所提出模型具有可行性和有效性。同时，本文与Ozawa et al. [23] ，Li et al. [24] ，Hesamianand Akbari (2018) [15] 和Hesamianand Akbari (2022) [25] 提出的模型进行了比较。拟合优度均值比较结果见表1。从表1可以看出，本文提出的模型获得很好的拟合效果，具有可行性和明显的拟合优势。

图2描述了模糊预测值与模糊时间序列观测值的差异，模糊预测值与模糊时间序列观测值越接近，说明模型拟合效果越好。从图2可以看出，与其他四个模型相比，本文模型得到的模糊预测值与模糊时间序列的观测值最接近，偏差最小。

Table 1. The performances of various fuzzy time series models in example analysis

表1. 算例分析中各模糊时间序列模型的拟合指标

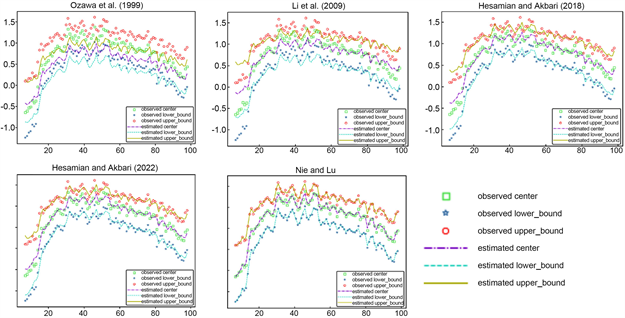
Figure 2. The observed and predicted values of each fuzzy time series model in example analysis

图2. 算例分析中各模糊时间序列模型输出的观测值和预测值

5. 结论

在许多时间序列建模中，与参数或非参数统计推断相比，半参数统计推断可能会产生稳健和灵活的结果。本文提出一种基于BP神经网络的自适应模糊时间序列半参数预测模型。该模型分别考虑了模糊数中心与其滞后阶之间的线性关系以及协变量之间的非线性关系，左展形和右展形和其滞后阶与中心估计值之间的关系。本文首次利用半参数技术建立了自适应回归模型中各元素之间的模糊关系。此外，基于非线性残差序列建立了BP神经网络，通过神经网络的运算得到了新的残差估计值，使得在模糊不确定条件下获得了更多的数据信息，提高了模型的预测精度。然后，本文采用一些常见的拟合优度准则，通过与现有模型的比较，验证了本文模型的可行性和有效性。最后，考虑多个异常值的组合存在的情况下，本文模型是否仍具有稳健性，将是以后研究的课题。

致谢

在此，我要感谢陆老师对这篇论文的指导。

NOTES

^*通讯作者。