量子非谐振子和双势阱模型中的六次与八次混合非谐项的基态能隙

The Ground-State Energy Gap of Sexic-Octic Mixed Anharmonicities in the Quantum Anharmonic Oscillator and the Double-Well Potential

摘要: 量子非谐振子和双势阱是重要的数学物理模型，其中，计算源自于非简谐项的基态能隙是一个重要的问题。对于含有纯非谐项的情况，我们最近的研究发现可以用同一个公式来描述它们源自于纯非谐项的基态能隙，意味着这两个模型中的非谐效应存在着某种联系。上述发现是关于的纯非谐项的情况，在本文中我们将继续关注含有混合非谐项的情况，我们计算了六次与八次混合非谐项所产生的基态能隙，发现它们仍然由同样的公式来描述，从而进一步确认了这种未知联系的存在性。

Abstract: The quantum anharmonic oscillator and the double-well potential models are important mathe-matical physics models in which the ground-state energy gap coming from the anharmonic terms is an important topic. For the case of pure anharmonic term, we find a qualitative formula that de-scribes the ground-state energy gap of both the anharmonic oscillator and the double-well poten-tial, which means that there is some connection between the anharmonic effects in the two models. The above discovery is about the case of pure anharmonic term, in this paper we will continue to focus on the case with mixed anharmonic term, we study this energy gap for the case of the sex-tic-octic mixed anharmonic term, and find that they are still described by the same qualitative formula, thus further confirming the existence of this unknown connection.

1. 引言

量子非谐振子和双阱势是两个重要的数学物理模型 [1] [2] [3] [4] ，其中的非谐效应是一个重要的研究问题，常通过计算其基态能隙中源自于非简谐项的部分来定量研究。在简谐极限下，通常用微扰的方法来计算该非谐能隙：非谐振子是围绕谐振子的物理图像展开微扰，其能级为渐近级数 [3] [5] ，而双势阱是围绕瞬子的物理图像展开 [6] ，解释了隧穿和衰变过程 [6] - [11] 。在强非谐效应时，通常由数值方法计算，因为它们的物理图像是未知的：强耦合问题在解析上一直是困难的，有很多逐阶求解的逼近方法，但是没有完整的闭合解析表达式。

对于含有纯非谐项的情况，我们在最近的研究 [12] [13] 中发现可以用同一个公式来描述它们源自于纯非谐项的非谐能隙，且该公式适应耦合参量的整个区间，这表明它们的非谐效应存在着某种统一的联系。因为谐振子和瞬子是两种完全不同的物理图像，所以这是一个深刻的联系。

本文进一步考虑具有混合非谐项的情况，对于六次与八次混合非谐项，我们发现这种联系仍然是存在的。由于这个定性公式适用于所有耦合区间，我们希望所发现的这个联系，能够有助于关于强耦合下的解析方法的寻找。

本文的计算采用数值bootstrap方法，这是一种非微扰方法，模型的能谱完全由自洽性条件中获得，不涉及任何微扰因素。数值bootstrap方法始于共形场论和矩阵模型的研究中 [14] [15] [16] [17] [18] ，其突破性进展发生在最近对于矩阵量子力学模型的研究里面 [19] ，此后，数值bootstrap方法迅速发展并产生了许多新的结果 [20] - [25] 。

2. 数值Bootstrap方法

Bootstrap方法的思想简洁，只用量子理论的基本假设来构建系统的自洽条件，求解这些自洽条件便可获得系统的解。但是具体求解这些自洽条件会出现解析上的复杂难题，因而人们开始探究bootstrap的数值实现。数值bootstrap算法主要分为以下三个步骤：求解递归方程、构造bootstrap矩阵、设置对应不同势函数的搜索空间，本文将沿用文献 [20] 的符号来简单介绍数值bootstrap算法。

2.1. 求解递归方程

对于一个给定哈密顿量的量子力学系统：

$H=\frac{p^2}{2}+V\left(x\right)$ (1)

假设能量E的本征态为 $|\phi \rangle$ (在下文的描述中省略了 $|\phi \rangle$ )，在能量本征态中，哈密顿量H和任意算子α都满足以下两个恒等式：

$\langle \left[H,\alpha \right]\rangle =0$ $\langle H\alpha \rangle =\langle \alpha H\rangle =E\langle \alpha \rangle$ (2)

将 $\alpha =x^n,x^{n}p$ 和哈密顿量H分别代入上式，运用对易关系可得到如下递归方程：

$n\left(n-1\right)\left(n-2\right)\langle x^{n-3}\rangle -8n\langle x^{n-1}V\left(x\right)\rangle +8nE\langle x^{n-1}\rangle -4\langle x^n{V}^{\prime }\left(x\right)\rangle =0$ (3)

2.2. 构造Bootstrap矩阵

采用 [20] 中构造矩阵的方法，选择如下算子：

$\mathcal{O}:={\displaystyle \underset{m=0}{\overset{K_x}{\sum }}{\displaystyle \underset{n=0}{\overset{K_p}{\sum }}{c}_{mn}{x}^m{p}^n}}$ (4)

其中 $c_{mn}$ 为一系列常数。任意算子 $\mathcal{O}$ 在能量本征态 $|\phi \rangle$ 上的期望值都满足正性约束条件

$\langle \left|{\mathcal{O}}^{†}\mathcal{O}\right|\rangle \ge 0$ (5)

上述条件限制bootstrap矩阵必须为半正定矩阵，这对算子的期望值有很强的约束作用，由此可以构造如下的bootstrap矩阵：

$\mathcal{M}:=\left(\begin{array}{ccc}{\mathcal{O}}_1^{†}{\mathcal{O}}_1& \cdots & {\mathcal{O}}_1^{†}{\mathcal{O}}_k\\ ⋮& \ddots & ⋮\\ {\mathcal{O}}_k^{†}{\mathcal{O}}_1& \cdots & {\mathcal{O}}_k^{†}{\mathcal{O}}_k\end{array}\right)\ge 0$ (6)

其中 ${\mathcal{O}}_{0,1,2,\cdots }$ 是 $\mathcal{O}$ 的组成元素(子算符)。称k为矩阵的深度，随着深度k的增加，约束会变得更强，哈密顿

量系统的能谱就会进一步的收敛。

2.3. 设置搜索空间

要使用递归关系，需要设置最小的数据集合来初始化递归，称这个集合为搜索空间。最小化搜索空间与哈密顿量的势能项有关，在谐振子中搜索空间只有一个变量E，在六次非谐振子中最小化搜索空间

为 $\left\{E,\langle x^2\rangle ,\langle x^4\rangle \right\}$ ，八次非谐振子的最小化搜索空间为 $\left\{E,\langle x^2\rangle ,\langle x^4\rangle ,x^6\right\}$ ，可见随着势能项次数的增加，

搜索空间中矩序列的次数会对应增加。本文使用的搜索空间与八次非谐振子的搜索空间相同。

我们选取了系统能量作为搜索参量，使用半正定优化算法来排除不满足约束条件的参数值。当深度k足够大时，剩余参数空间将收敛为一个很小的邻域，可将其视为一个数据点(原始参数空间的子集)，即为量子系统的离散特征值。

3. 模型

定义6次和8次混合非谐项的模型为

$H=\frac{p^2}{2}+g{x}^2+x^6+x^8$ (7)

其中耦合参数g代表着“质量”项， $g>0$ 对应着非谐振子， $g<\text{0}$ 对应着双势阱，当 $\left|g\right|\gg \text{1}$ 时系统表现出弱的非谐效应，当 $g\to \text{0}$ 时系统表现出强的非谐性。

图1给出了g = 1时具有混合非谐项的非谐振子的收敛能带，由图可以看出当深度k = 7时，基态已经分离，但分辨率较低。当深度增加到k = 10时，基态的范围进一步缩小，此时第一激发态也已经分离，随着k值的增加，基态能量会变为离散的数据点。

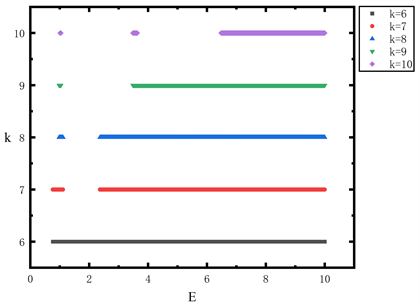
Figure 1. $g=1$ , bootstrap data of the anharmonic oscillator at different depth k

图1. $g=1$ ，不同深度值k下非谐振子的bootstrap数据

系统的基态E₀与第一激发态E₁间的基态能隙为 $\Delta E$ ，为了研究非谐项的贡献，需要从 $\Delta E$ 中剔除简谐项的贡献，从而得到非谐能隙，这需要对非谐振子和双势阱的物理图像进行分别考查。

对于非谐振子：由于简谐振子的能隙为 $\sqrt{2g}$ ，从能隙 $\Delta E$ 中减去简谐振子的贡献便是非谐能隙 $\Delta E^{\prime }$ ：

$\Delta E^{\prime }=\Delta E-\sqrt{2g}$ (8)

对于双势阱：当 $\left|g\right|\gg \text{1}$ 时系统表现出弱的非谐性，趋于两个简并的基态 $\Delta E\to 0$ ，当 $g\to \text{0}$ 时非谐效应增强产生了瞬子，导致了隧穿效应从而能级发生劈裂，因此可将非谐能隙视为 $\Delta E_D=\Delta E-0$ 。

对于这两种完全不同的物理图象，我们之前在研究纯非谐项的效应时发现，非谐振子的非谐能隙 $\Delta E^{\prime }$ 和双势阱的非谐能隙 $\Delta E_D$ 对耦合参数g的依赖关系，满足相同的经验公式 $F\left(g\right)$ ：

$F\left(g\right)=2F\left(0\right)\frac{{\text{e}}^{-a|g{|}^b}}{1+{\text{e}}^{-c|g{|}^d}},a,b,c,d>0$ (9)

其中a、b、c、d是待定的参数。在简谐极限 $\left|g\right|\to \infty$ 时，它为零，在强非谐效应 $\left|g\right|\to 0$ 时，它是g的收敛级数，这与两个模型的物理行为一致。

4. 结果讨论

本文针对6次和8次混合非谐项的情况，研究非谐振子的非谐能隙 $\Delta E^{\prime }$ 和双势阱的非谐能隙 $\Delta E_D$ 。

4.1. 双势阱

图2给出了E₀和E₁的bootstrap数据，可以看到，随着 $\left|g\right|$ 逐渐减小，非谐效应增强，双势阱的基态能隙增大。图3显示了非谐能隙 $\Delta E_D$ ，曲线为公式(9)的拟合， $\Delta E_D$ 在 $g=0$ 处最大，当 $\left|g\right|\gg \text{1}$ 时，逐渐趋近于零，符合预期。公式(9)与bootstrap数据非常吻合，拟合参数值见表1。

Table 1. Fitted parameter values

表1. 拟合参数值

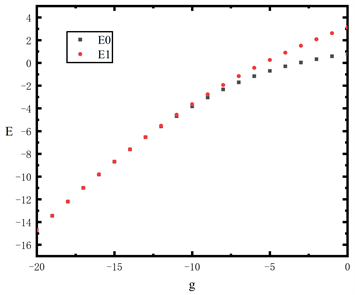
Figure 2. Energy levels E₀ and E₁ of the double well

图2. 双势阱能级E₀和E₁

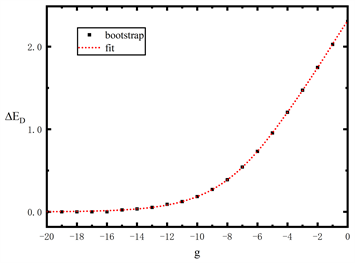
Figure 3. Energy gap ∆E_D due to anharmonicity

图3. 非谐能隙∆E_D

4.2. 非谐振子

图4显示了E₀和E₁的bootstrap数据。图5显示了由非谐效应产生的能隙 $\Delta E^{\prime }$ ，曲线为公式(9)的拟合。非谐能隙 $\Delta E^{\prime }$ 在 $g=0$ 时最大，当 $g\gg \text{1}$ 时，其渐近地趋近于零，符合预期。公式(9)与bootstrap数据非常吻合，拟合参数值见表1。

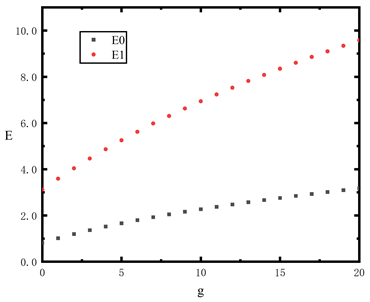
Figure 4. Energy levels E₀ and E₁ of the anharmonic oscillator

图4. 非谐振子能级E₀和E₁

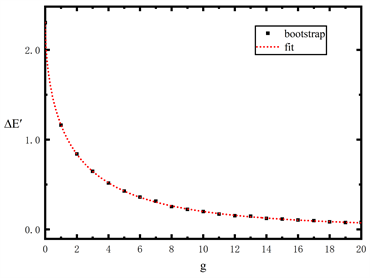
Figure 5. Energy gap $\Delta E^{\prime }$ due to anharmonicity

图5. 非谐能隙 $\Delta E^{\prime }$

4.3. 联系

非谐振子和双势阱具有完全不同的物理图像，因而它们的非谐效应的这种联系是意想不到的。在 [13] 中，我们提供了一个相变的视角来理解这种联系：把非谐振子 $g>0$ 和双阱势 $g<0$ 分别视为模型(7)的振子相和瞬子相，根据量子相变 [26] 的视角可以把非谐能隙看作序参量，描述了非谐效应。将 $\Delta E^{\prime }$ 和 $\Delta E_D$ 放在一起，如图6所示，其形状类似于相变中常见的 $\lambda$ 形曲线 [27] ，这提供了一种理解非谐振子与双阱势之间的非谐效应的视角。

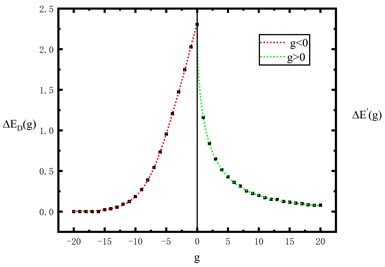
Figure 6. $\Delta E^{\prime }\left(g\right)$ and $\Delta E_D\left(g\right)$ for the quantum system (7)

图6. 量子模型(7)的非谐能隙 $\Delta E^{\prime }\left(g\right)$ 和 $\Delta E_D(\; g\; )$

5. 结论

本文考虑了含有六次与八次混合非谐项的量子非谐振子和双势阱模型，使用数值bootstrap方法计算了它们的非谐能隙 $\Delta E^{\prime }$ 和 $\Delta E_D$ ，本文的计算结果验证了它们都可以由公式(9)来描述，并且公式(9)同样也适用于含有纯非谐项的情况，本文的结果表明了这两种模型中的非谐效应存在着一个统一的联系，为了理解这种联系，本文提出了一个量子相变的视角。

希望本文的研究结果，有助于对于解析方法的寻找，来理解它们背后的未知联系，一个可能的方向是将能量解析延拓到复平面上 [28] [29] [30] [31] ，使用色散关系来研究其能谱关系。

基金项目

国家自然科学基金项目(批准号：12105121)。

参考文献