基于预测IRIME分数阶PID在线径控制系统中的应用

Application of FOPID on Diameter Control System Based on Prediction IRIME

摘要: 针对传统PID控制器对于非线性、时变性、大滞后的线径控制系统难以满足控制需求的问题。引入改进雾凇算法(IRIME)、模型预测算法(MPC)来对分数阶PID (FOPID)的控制参数进行优化。MPC算法通过系统阶跃响应，建立预测模型，对实际控制系统实现在线反馈校正，减少系统强滞后对线径控制精确度的影响，改善线径控制系统性能。通过对仿真结果的分析与评估，带预测IRIME的FOPID具有超调低、抗干扰性和鲁棒性好等优点。

Abstract: Considering the challenge that the traditional PID controller is difficult to satisfy the control needs of nonlinear, time-varying and strong lag wire diameter control system, the improved Rime algorithm (IRIME) and Model Prediction Algorithm (MPC) are introduced to optimize the control parameters of fractional PID (FOPID). MPC algorithm establishes a prediction model through the step response of the system, realizes online feedback correction for the actual control system, and reduces the influence of the strong lag of the system on the control effect of the control system. Through the analysis and evaluation of the simulation results, the FOPID with predicted IRIME has the advantages of low overshoot, good anti-interference and robustness.

1. 引言

当前正处于工业高速发展的新时期，工业和信息化部发布“十四五”规划，重视以信息传输为核心的传统通信基础设施建设，鼓励推动信息通信行业的发展。目前电线电缆行业无论在传输电能、信息传递、电气设备连接等领域都发挥着不可或缺的作用，因此对于电缆的质量提出了更高的要求。而电缆线径控制系统是电缆生产的重要工艺流程，电缆的线径精确程度直接影响到电缆质量 [1] [2] 。

伴随着科技的不断进步，对于电缆线径的精确度要求越来越高，分数阶PID在对控制精确度上相比于传统PID有更好的控制效果 [3] 。但分数阶PID增加了两个控制参数，在参数整定上存在一定的难度。对于强滞后、多干扰的线径控制系统，智能优化算法的优点有：对复杂系统适应性好，不需要人工调试经验。更多的学者也越来越重视智能控制算法的研究，采用粒子群法 [4] 、遗传算法 [5] 、布谷鸟算法 [6] 等智能优化算法寻找合适控制参数。Li H等人 [7] 提出蚁群算法与卡尔曼滤波结合来寻优控制参数并且控制系统扰动，但是计算复杂，实际应用对设备要求高。Sarkar M等人 [8] 提出Smith预估器来处理时间延迟，保持系统稳定，但是改变了系统传递函数模型，对于强滞后、多干扰的系统控制效果有待改善。Klopot T等人 [9] 在工业控制系统中引入自适应动态矩阵控制，对时变性、非线性、时延性的系统进行补偿，在控制性能上有一定程度的提高。

针对工业线径推挤系统，采用以上方法能在一定程度上解决线径推挤系统强滞后、多干扰的问题，对生产线径的精确度有一定的提高，但是对系统模型的精确度有较高的要求、对于提高系统的抗干扰性、鲁棒性上仍然存在一定的不足之处。本文引入改进的雾凇优化算法 [10] (Improved Rime Optimization Algorithm, IRIME)、模型预测控制(Model Predictive Control, MPC)和分数阶PID相结合，通过IRIME算法对于线径推挤系统的分数阶PID控制器的五个参数进行整定，采用MPC模型预测，改善系统的滞后性，降低系统控制的难度，使得系统可以及时对外部的多干扰进行及时的响应，以提高系统的鲁棒性，提高线径精确度。

2. 电缆生产系统

2.1. 电缆生产系统介绍

本文主要的研究对象是电缆生产系统，该系统主要的工艺流程是通过牵引直流伺服电机将电缆内芯通过塑料推挤机的穿线孔进入机筒加热通道，与此同时，将经过混料、熟化、压料的塑料胚料与电缆内芯混合，加热为熔融态，通过推挤电机和旋转螺杆的推挤作用，将塑料胚料包裹在电缆内芯表面，形成塑化电缆。之后通过机头的模具形成成型电缆，经过烧结炉和电火花机冷却后，形成定型电缆，绕卷到收线装置。

其中，烧结炉是用于将电缆线的金属芯和绝缘层紧密结合的设备，烧结炉可以提高电缆线的机械强度和耐热性。电火花机是用于检测电缆线表面是否有损伤或杂质的设备，它利用高压电脉冲在电缆线和工具电极之间产生火花，若电缆线表面有缺陷，火花就会穿透绝缘层，引起报警或断电。电缆生产系统示意图如图1所示。

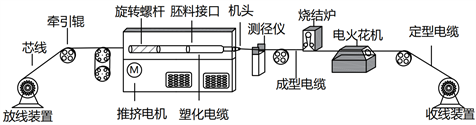
Figure 1. Schematic diagram of cable production system

图1. 电缆生产系统示意图

2.2. 系统数学模型建立

通过对线径推挤系统分析，在不考虑螺杆旋转机构和材料摩擦等原因的影响，线径推挤的厚度主要由牵引电机和螺杆旋转机构的推挤速度决定。故对牵引电机的调速系统进行分析，线径推挤系统采用电枢控制式直流电机调速。由电枢电路电压平衡方程、电机轴上的力矩方程式等直流电机关系式，可以得到电枢电压 $E_a$ 为输入量，负载转角 ${\theta }_m$ 为输出量的运动方程式，可表示为：

$L_{a}J\frac{{\text{d}}^3{\theta }_m}{\text{d}{t}^3}+\left(L_{a}B+R_{a}J\right)\frac{{\text{d}}^2{\theta }_m}{\text{d}{t}^2}+\left(R_{a}B+K_T{K}_e\right)\frac{\text{d}{\theta }_m}{\text{d}t}=K_T{e}_a$ (1)

考虑实际控制系统中，电枢回路的电感的大小可忽略不计，通过拉氏变换，其传递函数可表示为：

$\frac{{\theta }_m\left(s\right)}{E_a\left(s\right)}=\frac{K_T}{L_{\text{a}}J{s}^3+\left(L_{a}B+R_{a}J\right)s^2+\left(R_{a}B+K_T{K}_e\right)s}$ (2)

其中 $R_a$ 和 $L_a$ 分别为电枢电路中的电阻和电感， $E_a$ 为电枢电压， $K_e$ 为反电势常数， $K_T$ 为转矩常数。

由于刚被包裹的电缆线温度过高，为了避免线径测量仪由于电缆线的高温等因素造成损坏，侧径仪和出线口会保持一定距离。综上，直流电机调速系统可简化为一个二阶惯性环节，丝杆等机械传动机构和检测设备可简化为一个带比例增益的纯滞后环节。最终的电缆线径系统数学模型可简化为一个带纯滞后环节的二阶惯性环节，可表示为：

$G\left(s\right)=\frac{K{\text{e}}^{-\tau s}}{T_1{s}^2+T_{2}s+1}$ (3)

其中K为控制系统比例系数， $T_1$ 、 $T_2$ 为控制系统的大时间系数和小时间系数。 $\tau$ 为控制系统的纯滞后系数。

3. 雾凇优化算法及其改进

3.1. 标准雾凇优化算法

雾凇优化算法是一种启发于雾凇自然生长的物理现象的高效优化算法。雾凇的生长过程可分为软雾凇和硬雾凇两种，主要受自然中风速影响，通常软雾凇在微风环境生成，硬雾凇在强风环境生成。雾凇优化算法通过模拟软雾凇和硬雾凇的生长过程，构建软雾搜索策略和硬霜击穿机制，实现优化算法中的探索和开发。雾凇优化算法主要分为三个过程。

模拟软雾凇粒子在微风中的运动，提出软雾搜索策略，通过逐步探索的方法，实现大范围和小范围探索的切换，提高探索的效率和精确度。软雾搜索策略的公式可表示为：

$R_{ij}=R_{best,j}+RimeFactor\cdot \left[h\cdot \left(U{b}_{ij}-L{b}_{ij}\right)+L{b}_{ij}\right]$ (4)

$RimeFactor=r_1\cdot \cos \theta \cdot \beta$ (5)

$\theta =\pi t/10\cdot T$ (6)

$\beta =1-\left[\frac{w\cdot t}{T}\right]/w$ (7)

$E=\sqrt{t/T}$ (8)

其中RimeFactor是雾凇更新因素，用于对粒子进行更新。参数r₁是一个随机数范围(−1, 1)，用来控制粒子运动的方向。 $\beta$ 是环境因素，它遵循根据迭代的数量来模拟外部环境的影响，其数学模型为阶跃函数，用于保证算法的收敛性。t为当前迭代次数，T为算法的最大迭代次数。w为软雾时间系数，用于控制环境参数β的阶跃次数。E和r₂一起控制软雾搜索策略下粒子是否更新。

模拟硬雾凇在强风的交叉穿刺现象，提出硬霜穿刺机制。该机制通过最优粒子和其他粒子进行维度交叉互换，实现粒子之间信息有效传递。使用硬霜穿刺机制，可以在软雾搜索策略的基础上，提升算法的收敛速度并改善算法跳出局部最优的性能。硬霜穿刺机制的公式可表示为:

$R_{ij}=R_{best,j},r_3<F^{normr}\left(S_i\right)$ (9)

其中 $R_{ij}$ 为更新后第i组雾凇种群的第j个颗粒的新位置， $R_{best,j}$ 为在所有雾凇种群中的最佳雾凇组的第j个颗粒， $F^{normr}\left(S_i\right)$ 表示当前代理适应度值的归一化值，表示当前代理被选中的几率，r₃是[0 1]范围内的随机数。

对常规算法的贪婪选择机制进行扩展，提出增强贪婪选择机制。通常，常规优化算法有一种贪婪选择机制。典型的方法是对全局最优值与更新后的适应值比较，以更优值更新本次迭代的全局最优值，但此方法更多只能作为记录，对全局探索和开发效果较弱。因此提出增强贪婪选择机制。具体方法是，将更新后的适应度值与更新前相比较，如果更新后适应度更优，则进行替换，并替换对应雾凇组的粒子。

3.2. 改进雾凇优化算法

3.2.1. 引入次领导机制和自适应权重

由于适应度函数为多输入、单输出的算法结构，多重参数对于适应度函数的影响较为复杂，仅采用全局最优解作为领导解，往往使得后期算法群体对于某一组参数解过于趋同，难以跳出局部最优。故引入次领导机制，避免算法迭代到后期，算法群体过于聚集的情况，造成算力浪费。同时引入自适应权重改良算法，原始的权重默认设定为1，对于复杂的适应度函数，算法难以在开发与勘探之间进行权衡，因此引入新的自适应权重，来提高算法对于未知领域的开发与勘探的性能。引入次领导机制与自适应权重的目的是提升算法在寻优较为的复杂的适应度函数时跳出局部最优解的性能。次领导机制与自适应权重公式可表示为：

$\omega =\tanh \left(7.5\cdot {\left(t/T\right)}^2\right)+2.5$ (10)

$R_{ij}=\{\begin{array}{l}\omega \cdot R_{best,j}+{\alpha }_1,r_2<E\\ \omega \cdot R_{sec,j}+{\alpha }_2,r_2\ge E\&r_4<E\end{array}$ (11)

其中， $\omega$ 为自适应权重，考虑到算法步长系数是逐渐衰减，故此处自适应权重的目的是在算法初期适当减少对较优解的继承比例，使得算法在初期能够有更好的全局探索能力，加快全局收敛速度。 $R_{sec,j}$ 为全局最优领导和次优领导。r₄为新添加的随机值，取值范围为[0, 1]，作用是判断种群是否采用次领导机制。

3.2.2. 引入边界混沌映射与莱维飞行策略

为了进一步提高算法跳出局部最优的性能，引入边界混沌映射和莱维飞行组合策略。莱维飞行是一种满足非高斯分布的随机搜索策略，其飞行轨迹是由聚集的短步长和偶尔跳跃的长步长组成，在保证随机性的同时，也有较好的遍历性，有助于提升算法局部勘探能力。一般莱维飞行采用Mantegna进行拟合，以降低采用莱维分布带来的计算复杂度，可表示为：

$s=\frac{\mu }{{\left|\nu \right|}^{1/\gamma }}$ (12)

其中 $\mu ~N\left(0,{\sigma }_{\mu }^2\right)$ ， $\nu ~N\left(0,{\sigma }_{\nu }^2\right)$ ， ${\sigma }_{\mu }$ ， ${\sigma }_{\nu }$ 可表示为：

${\sigma }_{\mu }={\left\{\frac{\Gamma \left(1+\gamma \right)\sin \left(\pi \gamma /2\right)}{\gamma \cdot \Gamma \left[\left(1+\gamma \right)/2\right]\cdot 2^{\left(\gamma -1\right)/2}}\right\}}^{1/\gamma }$ (13)

${\sigma }_{\nu }=1,\gamma =1.5$ (14)

此次改进将莱维飞行策略与次领导机制相结合，则最优领导和次优领导步长 ${\alpha }_1$ 、 ${\alpha }_2$ 可表示为：

${\alpha }_1=RimeFactor\cdot \left[s\cdot \left(U{b}_{ij}-L{b}_{ij}\right)+L{b}_{ij}\right]$ (15)

${\alpha }_2=RimeFacto{r}_1\cdot \left[s\cdot \left(U{b}_{ij}-L{b}_{ij}\right)+L{b}_{ij}\right]$ (16)

$RimeFacto{r}_1=r_1\ast \sin \left(\left(\pi t/2T\right)+\pi \right)+1$ (17)

同时考虑到莱维飞行具有良好遍历性的同时，存在超出算法边界的可能，常规算法采用边界限幅来约束算法种群，但是被限幅的种群，往往由于适应度函数过大，不能对算法迭代做出贡献。故引入正弦混沌映射对边界种群进行处理，若种群某一维度粒子超过边界上限，则通过混沌反向映射到最优值和下限间，同理若这一维度粒子低于边界下限，则反向混沌映射到最优值和上限间。边界混沌映射可表示为：

$D=\left|\sin \left(1000\cdot R_{ij}\right)\right|$ (18)

$R_{ij}{}_{cor}=\{\begin{array}{l}D\cdot \left(U{b}_{ij}-R_{best,j}\right)+R_{best,j},R_{ij}<L{b}_{ij}\\ D\cdot \left(R_{best,j}-L{b}_{ij}\right)+L{b}_{ij},R_{ij}>U{b}_{ij}\end{array}$ (19)

4. 模型预测算法

4.1. 预测模型输出

实际系统的动态信息通过对象单位阶跃响应的采样值集合 $a_i=a\left(iT\right)$ ， $i=1,2,\cdots ,N$ 进行描述，N称为建模时域。当在k时刻，若考虑保持系统控制作用不发生改变的情况，则可以得出之后N个时刻的初始预测值 $y_0\left(k+i/k\right)$ ， $i=1,2,\cdots ,N$ 。其中 $\left(k+i/k\right)$ 表示k时刻对k + i时刻的预测。此时，对系统施加控制增量 $\Delta U_M\left(k\right)$ ，则系统对象的未来P个时刻的预测值可表示为：

$Y_{PM}\left(k\right)=Y_{P0}\left(k\right)+A\Delta U_M\left(k\right)$ (20)

$Y_{PM}\left(k\right)={\left[y_M\left(k+1/k\right),\cdot \cdot \cdot ,y_M\left(k+P/k\right)\right]}^{\text{T}}$ (21)

$Y_{P0}\left(k\right)={\left[y_0\left(k+1/k\right),\cdot \cdot \cdot ,y_0\left(k+P/k\right)\right]}^{\text{T}}$ (22)

$\Delta U_M\left(k\right)={\left[\Delta u\left(k\right),\cdot \cdot \cdot ,\Delta u\left(k+M-1\right)\right]}^{\text{T}}$ (23)

其中A为动态矩阵，由系统的阶跃响应参数构成， $Y_{PM}\left(k\right)$ 表示对控制增量 $\Delta U_M\left(k\right)$ 的预测向量， $Y_{P0}\left(k\right)$ 表示初始预测向量，M表示控制时域，P表示优化时域，N表示建模时域。根据对实际塑料胚料推挤控制系统的单位阶跃响应的研究，采用采样时间T = 1、N = 16、P = 13、M = 1作为预测模型控制参数。

4.2. 在线反馈校正

考虑到实际塑料胚料推挤控制系统存在模型失配、环境干扰等未知因素，未经反馈校正的预测线径有可能偏离实际线径。为了防止开环优化带来的误差，模型预测算法需要在k + 1时刻检测此时的实际值，并与k时刻对k + 1的预测值比较，用于补充对模型输出的预测，通过移位矩阵，实现时间基点变动，计算出k + 1时刻的预测初值，此值作为新的k时刻的预测初值。反馈校正公式可表示为：

$Y_{cor}\left(k+1\right)=Y_{N1}\left(k\right)+he\left(k+1\right)$ (24)

$Y_{cor}\left(k+1\right)={\left[y_{cor}\left(k+1/k+1\right),\cdot \cdot \cdot ,y_{cor}\left(k+N/k+1\right)\right]}^{\text{T}}$ (25)

$Y_{N0}\left(k+1\right)=S{Y}_{cor}\left(k+1\right)$ (26)

其中 $e\left(k+1\right)$ 为预测误差， $Y_{cor}\left(k+1\right)$ 为反馈校正后的向量， $Y_{N1}\left(k\right)$ 和 $Y_{N0}\left(k+1\right)$ 的第一个下标表示预测向量长度，第二个下标表示控制增量变化次数，h为权重系数构成的N维度矩阵。

5. IRIME-FOPID-MPC控制系统

雾凇预测分数阶PID控制分为预测和控制两个部分。建立IRIME-FOPID-MPC控制系统模型如图2所示。

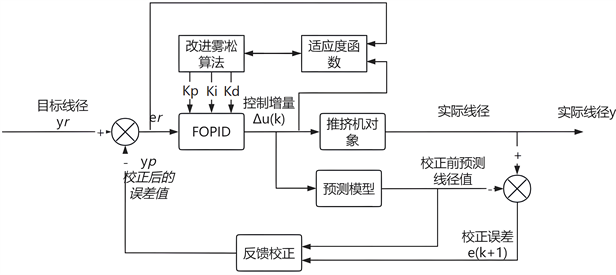
Figure 2. Model of the IRIME-FOPID-MPC control system

图2. IRIME-FOPID-MPC控制系统模型

其中预测部分的模型预测算法的功能是：预测之后一个时刻的预测初值，当时间来到下一时刻，根据机头测径仪的实际数值，对上次的预测初值进行校正，以提高控制系统的抗干扰性和动态性能。控制部分采用目标设定线径值与预测线径数值的差值作为控制器输入，通过IRIME算法对FOPID的五个参数进行整定，通过改变电机的输入电压，控制线径推挤系统的输出线径值。

FOPID (分数阶PID)控制器是基于传统PID控制器，将常规的积分器、微分器扩展至分数阶领域。则FOPID控制器可表示为：

$G\left(c\right)=K_P+K_I{s}^{-\lambda }+K_D{s}^{\mu }$ (27)

其中 $K_P$ 、 $K_I$ 、 $K_D$ 为比例、积分、微分系数。 $\lambda$ 和 $\mu$ 为分数阶积分系数、分数阶微分系数。

为保证改进雾凇算法整定出合适的分数阶PID参数，需要选取合适的适应度函数。适应度函数可表示为：

$J={\displaystyle {\int }_0^{\infty }\left(t^n\left|e\left(t\right)\right|+P\left(\delta \right)\left|e_1\left(t\right)\right|\right)\text{d}t}$ (28)

$P\left(\delta \right)=\{\begin{array}{l}100,\delta >0.45\%\\ 0,\delta \le 0.45\%\end{array}$ (29)

其中t为仿真时间， $e\left(t\right)$ 为线径值偏差信号， $\delta$ 为超调量。 $P\left(\delta \right)$ 为超调惩罚系数。n为时间系数，取值范围一般为[1, 1.2]。选取适合的适应度函数的情况下，一般认为适应度函数数值越小，控制系统的控制效果越好。

6. 系统仿真结果与结果分析

系统仿真选用MATLAB/SIMULINK为系统仿真平台。线径控制系统辨识采用江西某电缆生产企业的现场采集的数据： $K=0.61$ ， $\tau =1.1$ ， $T_1=1.309$ ， $T_2=2.39$ 。电缆线径系统数学模型可表示为：

$G\left(s\right)=\frac{0.61{\text{e}}^{-1.1s}}{1.309s^2+2.39s+1}$ (30)

设置RIME和IRIME的共同参数如下：最大迭代次数为100次，种群数量为30，迭代维度为5， $K_P$ 取值区间[0, 4]， $K_I$ 和 $K_D$ 取值区间[0, 1.5]， $\lambda$ 和 $\mu$ 取值区间[0, 1.5]。

6.1. 算法迭代效果分析

为了评估改进前后算法的迭代效果，采用RIME和IRIME分别对线径系统的分数阶PID参数多次迭代寻优，改进前后算法迭代效果对比图如图3所示。改进前后算法迭代数据如表1所示。

Table 1. Data of algorithm iterations before and after improvement

表1. 改进前后算法迭代数据

根据图3和表1分析，可以得出改进后的RIME算法全局收敛所需迭代数更少，经过34次迭代可以探寻到的适应值为23.6614，收敛速度得到一定程度的提高。并且相比标准RIME算法，改进后的RIME算法可以找出更低的全局最优值，探寻到的适应值为15.3242，具有更好的跳出局部陷阱的性能。

Figure 3. Comparison of algorithm iteration effect before and after improvement

图3. 改进前后算法迭代效果对比图

6.2. 系统阶跃响应、抗扰动性与鲁棒性分析

为了评估不同控制策略对线径控制系统的控制效果，设置目标线径为3.5 mm，仿真时间为60 s，在30 s处施加一个大小为1.2的扰动信号，系统阶跃响应以及抗干扰响应如图4所示。系统响应性能指标如表2所示。

Figure 4. Diagram of the system step response and anti-jamming response

图4. 系统阶跃响应以及抗干扰响应图

为了评估不同控制策略对线径控制系统鲁棒性的影响，修改目标线径为2.8 mm，仿真时间保持为60 s，将系统的纯滞后系数增加36%，根据修改参数前后的系统阶跃响应以及抗干扰响应响应曲线的变化，对系统的鲁棒性进行评估与分析，系统响应曲线如图5所示。

根据实验结果对不同策略的控制器进行性能评估，阶跃响应的结果表明：采用预测IRIME的FOPID控制器，在系统的三项动态性能指标上优于其他三种控制器。抗扰动性和鲁棒性测试结果表明：该控制器在面对外界扰动和系统内部参数变化的情况，有更佳的恢复平稳的性能。

Table 2. Data of system response performance index

表2. 系统响应性能指标数据

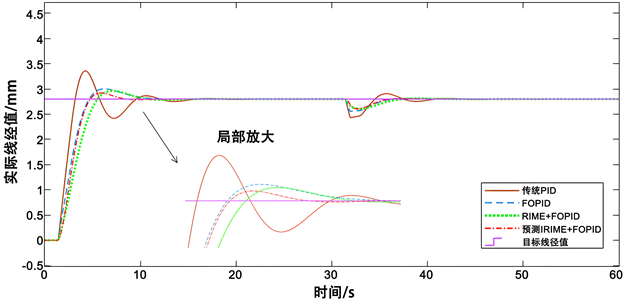
Figure 5. System response diagram after parameter changes

图5. 参数变动后的系统响应图

7. 结语

通过对线径控制系统的分析，提出改进雾凇优化算法和模型预测算法来优化分数阶PID的控制效果。最后根据不同策略的控制器下的仿真结果，对系统的阶跃响应、抗干扰性和鲁棒性测试效果作出分析与评估。算法迭代结果表明：相比标准RIME算法，改进后的RIME算法可以找出更低的全局最优值，具有更好的跳出局部陷阱的性能。阶跃响应的结果表明：采用预测IRIME的FOPID控制器，在系统的三项动态性能指标上优于其他三种控制器。抗扰动性和鲁棒性测试结果表明：该控制器在面对外界扰动和系统内部参数变化的情况，有更佳的恢复平稳的性能。综上，采用预测IRIME的FOPID控制器能较好地满足实际电缆线径控制的要求。

参考文献