由Lévy过程驱动的加权自排斥扩散的长时间行为和统计推断

Long Time Behavior and Statistical Inference of the Weighted Self-Repelling Diffusion Driven by Lévy Process

摘要: 假设是一个跳有界且界限为1的Lévy过程，生成三元组为。在本文中，我们考虑了由Lévy过程驱动的线性自排斥扩散方程，其中，和。这类过程是一类自交互扩散过程。我们研究了当t趋于无穷时解的长时间行为，发现它具有一种循环收敛性，这在此前的研究中尚未有类似的结论。进一步的，当w=0时在连续观测情况下，通过最小二乘法给出了方程参数的估计。我们证明了的估计量具有强相合性，并讨论了它的渐近分布。

Abstract: Let  be a Lévy process with jumps bounded by 1 and generating triplet . In this paper, as an attempt we consider the linear self-repelling diffusion driven by a Lévy process, , where  and the parameter . This process is similar to a type of self-interacting diffusion process. This paper studies the long time behaviour of the solution as t tends to infinity, and we find that it exhibits a cyclic convergence property, for which similar conclusions have not appeared in previous studies. In addition, when w=0, by using least squares method, we establish the strong consistency of the estimate  and discuss its asymptotic distribution under the consecutive observation.

1. 引言

1995年，Cranston和Le Jan [1] 介绍了一种特殊随机微分方程( 即线性自吸引扩散)

$X_t=B_t-\theta {\displaystyle {\int }_0^t{\displaystyle {\int }_0^s\left(X_s-X_r\right)\text{d}r}\text{d}s}+wt$ (1)

其中 $\theta >0$ 和 $\nu \in ℝ$ ，B是一个一维标准布朗运动。他们证明了当t趋于无穷时解的收敛性。这种路径依赖随机微分方程是由Durrett和Rogers [2] 首次提出，他们在1992年引入一类增长物模型

$X_t=B_t+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{s}f}}\left(X_s-X_u\right)\text{d}u\text{d}s$

其中B是一个d-维标准布朗运动，函数f是Lipschitz连续的。 $X_t$ 对应于t时刻聚合物末端的位置。在一定条件下，他们建立了随机微分方程解的渐近性态，并给出了一些猜想和问题。我们把这个解称为布朗运动与它自身通过的轨迹相互作用，即自交互作用的运动。一般来说，如果对f没有任何限制，方程(1)定义了一个自交互扩散。对任意 $x\in {ℝ}^d$ ，若 $x\cdot f\left(x\right)\ge 0$ (反之 $\le 0$ )，我们称之为自排斥扩散(反之，自吸引扩散)。换句话说，它更倾向于远离(或回到)之前达到的位置。更多相关结果可参考文献 [3] - [13] 及其参考文献。值得注意的是，自交互扩散与O-U过程相当。因此，我们可以得到它的渐近行为。自交互扩散也可以用来描述经济学中空间垄断竞争的一些行为。然而，目前研究的大多数方程都是由布朗运动驱动的。自然而然地，我们可以考虑由Lévy过程或高斯过程驱动的随机微分方程。通过分部积分，方程(1)可以改写为

$X_t=x+B_t+\theta {\displaystyle {\int }_0^t{\displaystyle {\int }_0^{s}r}}\text{d}{X}_r\text{d}s+wt,t\ge 0$

受此结果的启发，可以考虑方程

$X_t=x+B_t+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{s}g\left(r,X_r\right)\text{d}{X}_r}}\text{d}s+wt$

在本文中我们考虑

$X_t=L_t+\theta {\displaystyle {\int }_0^t{\displaystyle {\int }_0^s{\left(1+s\right)}^{\frac{1}{2}}\text{d}{X}_r}\text{d}s}+wt$ (2)

其中， $w\in ℝ,\theta >0$ 和 $L=\left\{L_t,t\ge 0\right\}$ 是 $ℝ$ 上跳有界且界为1的Lévy过程。记 ${\xi }_t={\displaystyle {\int }_0^t{\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+r\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_r}$ 。在第二章中，我们简要回顾Lévy过程的一些概念。第三章中设 $\theta >0$ ，我们证明了当t趋于无穷时，有

$J_t\left(0;\theta \right):={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{X}_t\to {\xi }_{\infty }+{\theta }^{-1}w$

以及

$J_t\left(n;\theta \right):=\theta {\left(1+t\right)}^{\frac{1}{2}}\left(J_t\left(n-1;\theta \right)-\left({\xi }_{\infty }+{\theta }^{-1}w\right){\lambda }_n\right)\to \left({\xi }_{\infty }+{\theta }^{-1}w\right){\lambda }_n$

在 $L^2$ 和几乎处处意义上存在，其中 ${\lambda }_n=2^{-n}\left[1\times 4\times \cdots \times \left(3n-2\right)\right]$ ， ${\xi }_{\infty }={\displaystyle {\int }_0^{\infty }{\left(1+s\right)}^{\frac{1}{2}}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_s$ 。这种循环收敛性是非常难得的。在此之前，对于由此类Lévy过程驱动的随机微分方程的研究非常有限，也没有出现类似关于解的循环收敛性的结论。第四章中，当 $w=0$ 时，在连续观测下我们估计了方程 的参数 $\theta$ ，得到了估计量 ${\hat{\theta }}_T$ 具有强相合性且当T趋于无穷大时，以下依分布收敛性成立：

${\left(1+T\right)}^{-\frac{1}{4}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left({\hat{\theta }}_T-\theta \right)\to \frac{2\theta L_1}{{\xi }_{\infty }}$

其中 $L_1$ 为一无限可分分布，并且 $L_1$ 和 ${\xi }_{\infty }$ 相互独立。

2. 预备知识

在本小节中，我们简要回顾 $ℝ$ 上Lévy过程的定义和性质。关于这些概念的背景，我们参考Applebaum [14] 和Sato [15] 。在本文中，我们考虑定义在概率空间 $\left(\Omega ,\mathcal{F},P,\left\{{\mathcal{F}}_t\right\}\right)$ 上的Lévy过程。为简单起见，我们让C代表一个正常数，仅取决于下标，其值在不同的情况下可能会有所不同。

定义在概率空间 $\left(\Omega ,\mathcal{F},P,\left\{{\mathcal{F}}_t\right\}\right)$ 上的随机过程 $L=\left\{L_t,t\ge 0\right\}$ ，如果它满足：

1) $L_0=0$ a.s；

2) L有独立、平稳增量；

3) L是随机连续的，即对任意 $\epsilon >0,s\ge 0$ ，

$\underset{t\to s}{\lim }P\left(\left|L_t-L_s\right|\ge \epsilon \right)=0$

我们称之为Lévy过程。定义在 $ℝ$ 上的Lévy过程 $L=\left\{L_t,t\ge 0\right\}$ 是半鞅，有如下Lévy-Itô分解：

$L_t=bt+B_t+{\displaystyle {\int }_{\left\{\left|y\right|<1\right\}}y\tilde{N}\left(t,\text{d}y\right)}+{\displaystyle {\int }_{\left\{\left|y\right|\ge 1\right\}}y}N\left(t,\text{d}y\right)$ (3)

其中， $b\in ℝ$ ， $B=\left\{B_t,t\ge 0\right\}$ 是一布朗运动，N是 ${ℝ}^{+}\times \left(ℝ-\left\{0\right\}\right)$ 上一独立泊松测度。若定义在 $ℝ$ 上的Lévy过程 $L=\left\{L_t,t\ge 0\right\}$ 跳有界，那么对一切正整数m，有

$E{\left|L_t\right|}^m<\infty$

此时，过程 $\bar{L}=\left\{L_t-E{L}_t,t\ge 0\right\}$ 是鞅过程。本文中，我们假设 $L_t$ 是一个跳有界且界限为1的Lévy过程，其生成三元组为 $\left(1,\nu ,0\right)$ ，由(3)我们有

$L_t=B_t+{\displaystyle {\int }_{\left\{\left|y\right|\ge 1\right\}}y\tilde{N}\left(t,\text{d}y\right)}$

对上述Lévy过程 $L=\left\{L_t,t\ge 0\right\}$ ，下方不等式成立：

$E\left[\underset{0\le t\le \tau }{\sup }{\left|{\displaystyle {\int }_0^t{u}_s}\text{d}{L}_s\right|}^p\right]\le C_p\left\{{\left({\displaystyle {\int }_0^{\tau }{u}_s^2}\text{d}s\right)}^{\frac{p}{2}}+{\left({\displaystyle {\int }_0^{\tau }{\displaystyle {\int }_{\left\{\left|y\right|<1\right\}}{y}^2{u}_s^{2}v\left(\text{d}y\right)\text{d}s}}\right)}^{\frac{p}{2}}+\left[{\displaystyle {\int }_0^{\tau }{\displaystyle {\int }_{\left\{\left|y\right|<1\right\}}{\left|y{u}_s\right|}^{p}v\left(\text{d}y\right)\text{d}s}}\right]\right\}$

和

$P\left(\underset{0\le t\le \tau }{\sup }\left|{\displaystyle {\int }_0^t{u}_s}\text{d}{L}_s\right|\ge \epsilon \right)\le C_p{\epsilon }^{-p}E\left[{\left|{\displaystyle {\int }_0^t{u}_{\tau }}\text{d}{L}_s\right|}^p\right]$

其中 $\text{math\_}$ ， $\tau$ 为停时， $u=\left\{u_t,t\ge 0\right\}$ 是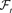-适应过程。

3. 自排斥条件下解的长时间行为

在本章中，我们考虑自排斥情况下的方程(2)。不难证明方程(2)有唯一解(参见Protter [16] )。定义核函数

$h_{\theta }\left(t,s\right)=1+\theta {\left(1+s\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_s^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}u}$

其中 $0\le s\le t$ ，并且对一切 $s\ge 0$ ，极限

$h_{\theta }\left(s\right):=\underset{t\to \infty }{\lim }{h}_{\theta }\left(t,s\right)=1+\theta {\left(1+s\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_s^{\infty }{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}u}$

存在。通过常数变易法，我们得到方程(2)的解

$X_t={\displaystyle {\int }_0^t{h}_{\theta }\left(t,s\right)\text{d}{L}_s}+w{\displaystyle {\int }_0^t{h}_{\theta }\left(t,s\right)\text{d}s}$

我们引入如下引理。

引理3.1 设 $\theta >0$ ，定义函数

$I_{\theta }\left(t\right)=\theta {\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}u}-1$

考虑函数列 $t\mapsto I_{\theta }\left(t;n\right):{ℝ}_{+}\to ℝ,n=1,2,\cdots$ ，有如下形式：

$I_{\theta }\left(t;1\right)=\theta {\left(1+t\right)}^{\frac{3}{2}}{I}_{\theta }\left(t\right),$

$I_{\theta }\left(t;n+1\right)=\theta {\left(1+t\right)}^{\frac{3}{2}}\left[I_{\theta }\left(t;n\right)-{\lambda }_n\right]$

其中 ${\lambda }_n=2^{-n}\left[1\times 4\times \cdots \times \left(3n-2\right)\right]$ 。那么，对 $n\ge 1$ ，

$\underset{t\to +\infty }{\lim }{I}_{\theta }\left(t,n\right)={\lambda }_n$ (4)

证明：仿照文献 [11] 的方法，对 $I_{\theta }\left(t\right)$ 进行 $n+1$ 次分部积分，那么对任意 $n\ge 1$ ，当t趋于无穷时有

$I_{\theta }\left(t\right)=\left[C_n+O\left({\left(1+t\right)}^{-\frac{3}{2}}\right)\right]{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }+\frac{1}{2\theta {\left(1+t\right)}^{\frac{3}{2}}}+\frac{1}{{\theta }^2{\left(1+t\right)}^3}+\cdots +\frac{1}{2^n{\theta }^n{\left(1+t\right)}^{\frac{3}{2}n}}{\displaystyle \underset{i=1}{\overset{n}{\prod }}\left(3i-2\right)}+{\Delta }_{\theta }\left(t,n\right)$

其中

${\Delta }_{\theta }\left(t,n\right)=-{\displaystyle \underset{i=1}{\overset{n+2}{\prod }}\left(3i-5\right)}\frac{{\left(1+t\right)}^{\frac{1}{2}}}{2^{n+2}{\theta }^n}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t\left({\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }-{\displaystyle \underset{j=0}{\overset{n}{\sum }}{\left(\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta \right)}^j}\right)\frac{\text{d}u}{{\left(1+u\right)}^{\frac{3}{2}n-\frac{3}{2}}}}$

结合 $I_{\theta }\left(t;n\right)$ 的定义，对任意整数 $n\ge 2$ ，有

$\begin{array}{c}{I}_{\theta }\left(t,1\right)=\theta {\left(1+t\right)}^{\frac{3}{2}}{I}_{\theta }\left(t\right)=\theta {\left(1+t\right)}^{\frac{3}{2}}\left[C_n+O{\left(1+t\right)}^{-\frac{3}{2}}\right]{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\\ +\frac{1}{2}+\frac{1}{\theta {\left(1+t\right)}^{\frac{3}{2}}}+\cdots +\frac{1}{2^n{\theta }^{n-1}{\left(1+t\right)}^{\frac{3}{2}n-\frac{3}{2}}}{\displaystyle \underset{i=1}{\overset{n}{\prod }}\left(3i-2\right)}+\theta {\left(1+t\right)}^{\frac{3}{2}}{\Delta }_{\theta }\left(t,n\right)\left(t\to \infty \right)\end{array}$

和

$\begin{array}{l}{I}_{\theta }\left(t,2\right)=\theta {\left(1+t\right)}^{\frac{3}{2}}\left(I_{\theta }\left(t,1\right)-{\lambda }_1\right)={\theta }^2{\left(1+t\right)}^3\left[C_n+O{\left(1+t\right)}^{-\frac{3}{2}}\right]{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\\ +1+\frac{7}{2\theta {\left(1+t\right)}^{\frac{3}{2}}}+\cdots +\frac{1}{2^n{\theta }^{n-2}{\left(1+t\right)}^{\frac{3}{2}n-3}}{\displaystyle \underset{i=1}{\overset{n}{\prod }}\left(3i-2\right)}+{\theta }^2{\left(1+t\right)}^3{\Delta }_{\theta }\left(t,n\right)\left(t\to \infty \right)\end{array}$

又因为对于任意的整数 $1\le m\le n$ ，当t趋于无穷时，

${\left(1+t\right)}^{\frac{3}{2}m}{\Delta }_{\theta }\left(t,n\right)\to 0$

所以有

$\begin{array}{l}{I}_{\theta }\left(t,n\right)={\theta }^n{\left(1+t\right)}^{\frac{3}{2}n}\left[C_n+O\left({\left(1+t\right)}^{-\frac{3}{2}}\right)\right]{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }+2^{-n}{\displaystyle \underset{i=1}{\overset{n}{\prod }}\left(3i-2\right)}\\ +{\theta }^n{\left(1+t\right)}^{\frac{3}{2}n}{\Delta }_{\theta }\left(t,n\right)\to {\lambda }_n\left(t\to \infty \right)\end{array}$

也就表明收敛性(4)成立。

引理3.2 设 $\theta >0$ ，定义函数

${\xi }_t:={\displaystyle {\int }_0^t{\left(1+s\right)}^{\frac{1}{2}}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_s,t\ge 0$

过程 $\xi =\left\{{\xi }_t,t\ge 0\right\}$ 和随机变量 $\text{math\_}$ 在 $L^2$ 上是适定的。当t趋于无穷时，

${\eta }_t:={\left(1+t\right)}^{\frac{3n}{2}}\varphi \left(t\right)\left({\xi }_t-{\xi }_{\infty }\right)\to 0$ (5)

在 $L^2$ 和几乎处处意义下成立，其中 $n\ge 1$ 和 $\varphi \left(t\right)={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}s$ 。

证明 给定 $\theta >0$ ，记 $h_{\nu }={\displaystyle {\int }_{\left|y\right|<1}{y}^2}\nu \left(\text{d}y\right)<\infty$ 。对 $t>0$ ，有

$\begin{array}{c}E{\left|{\xi }_t\right|}^2={\displaystyle {\int }_0^t\left(1+s\right){\text{e}}^{\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }\text{d}s}+{\displaystyle {\int }_0^t{\displaystyle {\int }_{\left|y\right|<1}{y}^2\left(1+s\right){\text{e}}^{\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }\nu \left(\text{d}y\right)\text{d}s}}\\ =\left(1+h_{\nu }\right){\displaystyle {\int }_0^t\left(1+s\right){\text{e}}^{\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }\text{d}s}<\left(1+h_{\nu }\right){\displaystyle {\int }_0^{\infty }\left(1+s\right){\text{e}}^{\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }\text{d}s}<\infty \end{array}$

此外，当t趋于无穷时，基于 $\varphi \left(t\right)\to {\theta }^{-1}$ 以及

${\left(1+t\right)}^{3n}E{\left|{\xi }_t-{\xi }_{\infty }\right|}^2={\left(1+t\right)}^{3n}\left(1+h_{\nu }\right){\displaystyle {\int }_t^{\infty }\left(1+s\right){\text{e}}^{-\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }\text{d}s}\to 0$

我们得到收敛性(5)在 $L^2$ 上成立。现证明它依概率1收敛。对任意 $n\ge 1$ ，当t趋于无穷时，

$\begin{array}{l}{\left(1+t\right)}^{\frac{3n}{2}}\left({\xi }_{\infty }-{\xi }_t\right)={\left(1+t\right)}^{\frac{3n}{2}}{\displaystyle {\int }_t^{\infty }{\left(1+s\right)}^{\frac{1}{2}}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_s\\ =-{\left(1+t\right)}^{\frac{3n+1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{L}_t-\frac{1}{2}{\left(1+t\right)}^{\frac{3n}{2}}{\displaystyle {\int }_t^{\infty }{L}_s{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left({\left(1+s\right)}^{-\frac{1}{2}}-2\theta \left(1+s\right)\right)\text{d}s}\to 0\end{array}$

几乎处处成立。进一步地，当t趋于无穷时，

${\eta }_t\stackrel{a.s}{\to }0$

我们得到了引理。

引理3.3 假设 $\theta >0$ ，函数 $I_{\theta }$ 为引理3.1中定义得函数，则

$\underset{t\to \infty }{\lim }{\left(1+t\right)}^{\frac{3}{2}}{I}_{\theta }\left(t\right)=\frac{1}{2\theta }$

和

$\underset{t\to \infty }{\lim }{\left(1+t\right)}^{\frac{5}{2}}{I^{\prime }}_{\theta }\left(t\right)=-\frac{3}{4\theta }.$

证明 给定 $\theta >0$ ，利用洛必达法则，可以得到

$\begin{array}{c}\underset{t\to \infty }{\lim }{\left(1+t\right)}^{\frac{3}{2}}{I}_{\theta }\left(t\right)=\underset{t\to \infty }{\lim }{\left(1+t\right)}^{\frac{3}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left(-{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }+\theta {\left(1+t\right)}^{\frac{1}{2}}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}s\right)\\ =\underset{t\to \infty }{\lim }{\left(1+t\right)}^{\frac{3}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left(-{\displaystyle {\int }_0^t\theta }{\left(1+s\right)}^{\frac{1}{2}}{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}s-1+\theta {\left(1+t\right)}^{\frac{1}{2}}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}s\right)\\ =\underset{t\to \infty }{\lim }\theta {\left(1+t\right)}^{\frac{3}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left[{\left(1+t\right)}^{\frac{1}{2}}-{\left(1+s\right)}^{\frac{1}{2}}\right]\text{d}s}=\frac{1}{2\theta }\end{array}$

当 $t\ge 0$ 时，显然

$\begin{array}{c}{I^{\prime }}_{\theta }\left(t\right)=\frac{\theta }{2}{\left(1+t\right)}^{-\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}u+\theta {\left(1+t\right)}^{\frac{1}{2}}-{\theta }^2\left(1+t\right){\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}u\\ =\theta {\left(1+t\right)}^{-\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left(\frac{1}{2}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}u+\left(1+t\right){\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }-\theta {\left(1+t\right)}^{\frac{3}{2}}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}u\right)\\ =\theta {\left(1+t\right)}^{-\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\left(\frac{1}{2}-\theta {\left(1+t\right)}^{\frac{3}{2}}+\theta \left(1+t\right){\left(1+u\right)}^{\frac{1}{2}}\right)\text{d}u+\theta {\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\end{array}$

令

$f_{\theta }\left(t\right)={\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\left(\frac{1}{2}-\theta {\left(1+t\right)}^{\frac{3}{2}}+\theta \left(1+t\right){\left(1+u\right)}^{\frac{1}{2}}\right)\text{d}u$

其中 $\theta >0$ ，则对任意的 $t\ge 0$ ，显然有 $f_{\theta }\left(0\right)=0$ 和

${I^{\prime }}_{\theta }\left(t\right)=\theta {\left(1+t\right)}^{-\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left(f_{\theta }\left(t\right)+1\right)$

另一方面，对任意的 $t\ge 0$ ，当t趋于无穷时，有

$\begin{array}{c}{f^{\prime }}_{\theta }\left(t\right)={\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left(-\frac{3}{2}\theta {\left(1+t\right)}^{\frac{1}{2}}+\theta {\left(1+u\right)}^{\frac{1}{2}}\right)\text{d}u}+\frac{1}{2}{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\\ =-\frac{3}{2}\theta {\left(1+t\right)}^{\frac{1}{2}}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}u+\theta {\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}{\left(1+u\right)}^{\frac{1}{2}}\text{d}u+\frac{1}{2}{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\\ =-\frac{3}{2}\theta {\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left[{\left(1+t\right)}^{\frac{1}{2}}-{\left(1+u\right)}^{\frac{1}{2}}\right]\text{d}u}+\frac{1}{2}\\ =-\frac{3}{4}\theta {\displaystyle {\int }_0^t{\left(1+u\right)}^{-\frac{1}{2}}\text{d}u}{\displaystyle {\int }_0^u{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}s}+\frac{1}{2}\to -\infty \end{array}$

和 ${f^{\prime }}_{\theta }\left(t\right)\le \frac{1}{2}$ 成立。则

$f_{\theta }\left(t\right)={\displaystyle {\int }_0^t{f^{\prime }}_{\theta }\left(s\right)\text{d}s}\to \infty \left(t\to \infty \right)$

由洛必达法则得，

$\begin{array}{c}\underset{t\to \infty }{\lim }{\left(1+t\right)}^{\frac{5}{2}}{I^{\prime }}_{\theta }\left(t\right)=\underset{t\to \infty }{\lim }\theta {\left(1+t\right)}^2{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{f}_{\theta }\left(t\right)\\ =\underset{t\to \infty }{\lim }\frac{-3\theta }{2{\left(1+t\right)}^{-\frac{3}{2}}{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left[{\left(1+t\right)}^{\frac{1}{2}}-{\left(1+u\right)}^{\frac{1}{2}}\right]\text{d}u}\\ =-\frac{3}{4\theta }\end{array}$

证毕。

引理3.4 假设 $\theta >0$ ， $I_{\theta }\left(t\right)$ 为引理3.1中所定义函数，则随机变量 ${\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(s\right)\text{d}{L}_s$ 在 $L^2$ 意义下存在并且

${\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{L}_s\to {\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(s\right)\text{d}{L}_s\left(t\to \infty \right)$

在 $L^2$ 和几乎处处意义下成立。

证明 给定 $\theta >0$ ，对一切 $t\ge 0$ ，有 $\underset{t\to \infty }{\lim }{I}_{\theta }\left(t\right)=0$ 。由引理3.3得，对任意的 $t\ge 0$ ，下列连续性成立：

$\left|I_{\theta }\left(t\right)\right|\le C_{\theta }{\left(1+t\right)}^{-\frac{3}{2}}$ (6)

$\left|{I^{\prime }}_{\theta }\left(t\right)\right|\le C_{\theta }{\left(1+t\right)}^{-\frac{5}{2}}$ (7)

显然当 $t\ge 0$ 时有

$E{\left|{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{L}_s\right|}^2=\left(1+h_{\nu }\right){\displaystyle {\int }_0^t{I}_{\theta }}{\left(s\right)}^2\text{d}s<\left(1+h_{\nu }\right){\displaystyle {\int }_0^{\infty }{I}_{\theta }}{\left(s\right)}^2\text{d}s<\infty$

我们考虑当t趋于无穷时， ${\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{L}_s$ 的收敛性。记

${\Psi }_t={\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(s\right)\text{d}{L}_s-{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{L}_s={\displaystyle {\int }_t^{\infty }{I}_{\theta }}\left(s\right)\text{d}{L}_s$

当t趋于无穷时，由(6)我们有

$E{\left|{\Psi }_t\right|}^2=\left(1+h_{\nu }\right){\displaystyle {\int }_t^{\infty }{I}_{\theta }}{\left(s\right)}^2\text{d}s~{\left(1+t\right)}^{-2}\to 0$

接下来，我们证明对一切 $\theta >0$ ，当t趋于无穷时 ${\Psi }_t$ 几乎处处收敛到零。当t趋于无穷时，通过(6)、(7)和分部积分，显然有

${\Psi }_t={\displaystyle {\int }_t^{\infty }{I}_{\theta }}\left(s\right)\text{d}{L}_s=-I_{\theta }\left(t\right)L_t-{\displaystyle {\int }_t^{\infty }{L}_s}{I^{\prime }}_{\theta }\left(s\right)\text{d}s\to 0$

几乎处处成立，引理得证。

定理3.5 假设 $\theta >0$ 。当 $t\to \infty$ 时，

$J_t\left(0;\theta \right):={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{X}_t\to {\xi }_{\infty }+{\theta }^{-1}w$

在 $L^2$ 和几乎处处意义下收敛。

证明 给定 $\theta >0$ 。当 $t\ge 0$ 时有

$\begin{array}{c}{J}_t\left(0;\theta \right)={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{X}_t\\ ={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left({\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}{L}_s+w{\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}s\right)\\ ={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{L}_t+\theta {\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}{\xi }_u\text{d}u\\ +w{\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}s\end{array}$

通过分部积分，有

$\begin{array}{c}{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left({\xi }_u-{\xi }_{\infty }\right)\text{d}u}=-{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}{\displaystyle {\int }_u^{\infty }{\left(1+s\right)}^{\frac{1}{2}}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_s\text{d}u\\ =-{\displaystyle {\int }_0^t{\left(1+s\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^s{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}u}\text{d}{L}_s}\\ -{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}u}{\displaystyle {\int }_t^{\infty }{\left(1+s\right)}^{\frac{1}{2}}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_s\\ \equiv {\zeta }_t\left(1\right)-{\zeta }_t(\; 2\; )\end{array}$

又因为对任意 $t\ge 0$ ，

${\displaystyle {\int }_0^t{h}_{\theta }\left(t,s\right)\text{d}s}={\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\text{d}u}$

所以有

$\begin{array}{l}{J}_t\left(0;\theta \right)-\left({\xi }_{\infty }+{\theta }^{-1}w\right)\\ ={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{L}_t+\theta {\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left({\zeta }_t\left(1\right)-{\zeta }_t\left(2\right)\right)+\left({\xi }_{\infty }+{\theta }^{-1}w\right)I_{\theta }\left(t\right)\\ =\left({\xi }_{\infty }+{\theta }^{-1}w\right)I_{\theta }\left(t\right)-{\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{I}_{\theta }\left(s\right)\text{d}{L}_s}-\theta \varphi \left(t\right)\left({\xi }_{\infty }-{\xi }_t\right)\end{array}$ (8)

因此，当t趋于无穷时，由事实

$\frac{L_t}{t}\to 0$

在 $L^2$ 和几乎处处意义下成立以及引理3.1、引理3.2和引理3.4可得，

$J_t\left(0;\theta \right)-\left({\xi }_{\infty }+{\theta }^{-1}w\right)\to 0$

在 $L^2$ 和几乎处处意义下成立。

定理3.6 假设 $\theta >0$ 。定义递推过程 $J\left(n;\theta \right)=\left\{J_t\left(n;\theta \right),t\ge 0\right\},n=0,1,2,\cdots$ ，即，

$J_t\left(0;\theta \right):={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{X}_t$

$J_t\left(n;\theta \right):=\theta {\left(1+t\right)}^{\frac{3}{2}}\left(J_t\left(n-1;\theta \right)-\left({\xi }_{\infty }+{\theta }^{-1}w\right){\lambda }_{n-1}\right)$

则对任意 $n\ge 0$ ，当t趋于无穷时，

$J_t\left(n;\theta \right)\to \left({\xi }_{\infty }+{\theta }^{-1}w\right){\lambda }_n$

在 $L^2$ 和几乎处处意义下成立，其中 $X_t$ 是方程(2)的解且 ${\lambda }_0=1$ 。

证明 给定 $\theta >0$ 。当 $t\ge 0$ 时，(8)表明对任意 $t>0$ 和 $n\ge 1$ ，

$\begin{array}{c}{J}_t\left(n;\theta \right)=\theta {\left(1+t\right)}^{\frac{3}{2}}\left(J_t\left(n-1;\theta \right)-\left({\xi }_{\infty }+{\theta }^{-1}w\right){\lambda }_{n-1}\right)\\ =\left({\xi }_{\infty }+{\theta }^{-1}w\right)I_{\theta }\left(t,n\right)-{\theta }^n{\left(1+t\right)}^{\frac{3n+1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{L}_s-{\theta }^{n+1}{\left(1+t\right)}^{\frac{3n}{2}}\varphi \left(t\right)\left({\xi }_{\infty }-{\xi }_t\right)\end{array}$

其中 $I_{\theta }\left(t\right)$ 是引理3.1中定义的。因此，该定理的证明可以由(4)、(5)和引理3.4得到。

4. 统计推断

在本章中，我们研究微分方程

$\text{d}{X}_t=\text{d}{L}_t+\theta \left({\displaystyle {\int }_0^t{\left(1+s\right)}^{\frac{1}{2}}}\text{d}{X}_s\right)\text{d}t$

在连续观测下的参数估计。记 $Y_t={\displaystyle {\int }_0^t{\left(1+r\right)}^{\frac{1}{2}}\text{d}{X}_r}$ 。 $\theta$ 的最小二乘估计量可由以下比较函数的最小值求出：

$\rho \left(\theta \right)={\displaystyle {\int }_0^T{\left({\stackrel{\dot{}}{X}}_t-\theta Y_t\right)}^2}\text{d}t$

得到 $\theta$ 的最小二乘估计量

${\hat{\theta }}_T=\frac{{\displaystyle {\int }_0^T{Y}_t}\text{d}{X}_t}{{\displaystyle {\int }_0^T{Y}_t^2}\text{d}t}$

由常数变易法得

$Y_t={\text{e}}^{\frac{2}{3}\theta \left(1+t\right)-\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\left(1+s\right)}^{\frac{1}{2}}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\text{d}{L}_s={\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }{\xi }_t$ (9)

为了研究参数的相合性和渐近分布，我们引入了一个引理。

引理4.1 当T趋于无穷时，有如下依分布收敛成立：

${\left(1+T\right)}^{\frac{1}{4}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{L}_s\to L_1$

其中随机变量 $L_1$ 服从三元组 $\left({\left(2\theta \right)}^{-\frac{1}{2}},K_T^{-1}\nu ,0\right)$ 的无限可分分布， $K_T={\left(1+T\right)}^{\frac{1}{4}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}s$ 。

证明 显然，对任意 $T>0$ ，有

${\left(1+T\right)}^{\frac{1}{4}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{L}_s=L_1$

其中 $L_1$ 服从一个无限可分分布，生成三元组为 $\left(A,{\nu }_1,0\right)$ 。这里等号“=”表示分布相等。我们知道 $L_t$ 的特征函数如下：

${\phi }_{L_t}\left(u\right)=E\left[{\text{e}}^{\left\{i\langle L_t,u\rangle \right\}}\right]=\exp \left\{-\frac{1}{2}t\langle u,u\rangle +t{\displaystyle {\int }_{{ℝ}_0}\left({\text{e}}^{i\left(u,x\right)}-1-i\langle u,x\rangle \right)v\left(\text{d}x\right)}\right\}$

记

$M_t={\displaystyle {\int }_{\left|y\right|<1}y}{\left(1+T\right)}^{\frac{1}{4}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\tilde{N}\left(\text{d}s,\text{d}y\right)=K_T{\displaystyle {\int }_{\left|y\right|<1}y}\tilde{N}\left(\text{d}y,s\right)$

于是我们可以得到

$E\left[{\text{e}}^{\left\{i\langle M_t,u\rangle \right\}}\right]=\exp \left\{t{\displaystyle {\int }_{{ℝ}_0}\left({\text{e}}^{i\langle u,K_{T}x\rangle }-1-i\langle u,K_{T}x\rangle \right)v\left(\text{d}x\right)}\right\}=\exp \left\{t{\displaystyle {\int }_{{ℝ}_0}\left({\text{e}}^{i\langle u,x\rangle }-1-i\langle u,x\rangle \right)}\left(v{K}^{-1}\right)\left(\text{d}x\right)\right\}$

故我们得到了 ${\nu }_1=K_T^{-1}$ 以及

$\begin{array}{c}A=\underset{T\to \infty }{\lim }{\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }E{\left|{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{B}_s\right|}^2\\ =\underset{T\to \infty }{\lim }{\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }{\displaystyle {\int }_0^T{\text{e}}^{\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }}\text{d}s=\frac{1}{2\theta }\end{array}$

引理得证。

定理4.1 假设 $\theta >0$ ，则估计量 $\hat{\theta }$ 是强相合的，换句话说，当T趋于无穷时，

$\hat{\theta }\to \theta$

几乎必然成立。进一步地，当T趋于无穷大时，以下依分布收敛性成立：

${\left(1+T\right)}^{-\frac{1}{4}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left({\hat{\theta }}_T-\theta \right)\to \frac{2\theta L_1}{{\xi }_{\infty }}$

其中 $L_1$ 如引理4.1中所定义，并且 $L_1$ 和 ${\xi }_{\infty }$ 相互独立。

证明 由分部积分可得

${\displaystyle {\int }_0^T{Y}_t}\text{d}{L}_t=Y_T{L}_T-{\displaystyle {\int }_0^T{L}_t\text{d}{Y}_t}=Y_T{L}_T-\theta {\displaystyle {\int }_0^T{\left(1+t\right)}^{\frac{1}{2}}{L}_t{Y}_t\text{d}t}-{\displaystyle {\int }_0^T{\left(1+t\right)}^{\frac{1}{2}}{L}_t\text{d}{L}_t}$

结合(9)、引理3.2和洛必达法则，可以证明当T趋于无穷大时，以下收敛以概率1成立：

${\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }{\displaystyle {\int }_0^T{Y}_t{}^2}\text{d}t\to \frac{{\xi }_{\infty }^2}{2\theta }$

$\begin{array}{l}{\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }{Y}_T{L}_T=\frac{L_T}{T}\cdot T{\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\xi }_T\to 0\\ {\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }{\displaystyle {\int }_0^T{\left(1+t\right)}^{\frac{1}{2}}{L}_t{Y}_t\text{d}t}=\frac{{\left(1+T\right)}^2}{{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\cdot \frac{{\displaystyle {\int }_0^T{\left(1+t\right)}^{\frac{1}{2}}{L}_t{Y}_t\text{d}t}}{{\left(1+T\right)}^{\frac{3}{2}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\to 0\end{array}$

此外，当T趋于无穷大时有

${\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^T{\left(1+t\right)}^{\frac{1}{2}}{L}_t}\text{d}{L}_t=\frac{1}{2}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }\left[{\left(1+T\right)}^{\frac{1}{2}}{L}_T^2-\frac{1}{2}{\displaystyle {\int }_0^T{\left(1+t\right)}^{-\frac{1}{2}}{L}_t^2\text{d}t}\right]\to 0$

综合以上结论，我们可以得到：

${\hat{\theta }}_T-\theta =\frac{{\displaystyle {\int }_0^T{Y}_t}\text{d}{X}_t}{{\displaystyle {\int }_0^T{Y}_t^2}\text{d}t}-\theta =\frac{{\displaystyle {\int }_0^T{Y}_t}\text{d}{L}_t}{{\displaystyle {\int }_0^T{Y}_t^2}\text{d}t}\to 0$

几乎必然成立。接下来我们考虑估计量 $\hat{\theta }$ 的渐近分布。对任意 $T>0$ ，我们有

${\left(1+T\right)}^{-\frac{1}{4}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left({\hat{\theta }}_T-\theta \right)=\frac{{\left(1+T\right)}^{-\frac{1}{2}}{\text{e}}^{\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }}{{\displaystyle {\int }_0^T{Y}_t^2}\text{d}t}\frac{{\displaystyle {\int }_0^T{Y}_t}\text{d}{L}_t}{{\left(1+T\right)}^{-\frac{1}{4}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}$

记 $m_t={\left(1+t\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^t{\text{e}}^{\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{L}_s$ ，对任意 $T>0$ ，有

$\begin{array}{c}{\displaystyle {\int }_0^T{Y}_t}\text{d}{L}_t={\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}{\xi }_t\text{d}{L}_t={\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}{\xi }_T\text{d}{L}_t+{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left({\xi }_t-{\xi }_T\right)\text{d}{L}_t}\\ ={\xi }_T{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{L}_t-{\displaystyle {\int }_0^T{\left(1+s\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^s{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{L}_t\text{d}{L}_s}\\ ={\xi }_T{\displaystyle {\int }_0^T{\text{e}}^{\frac{2}{3}\theta {\left(1+t\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\text{d}{L}_t-{\displaystyle {\int }_0^T{m}_s}\text{d}{L}_s\end{array}$

当T趋于无穷时，由

$\begin{array}{l}{\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }E{\left|{\displaystyle {\int }_0^T{m}_s}{L}_s\right|}^2={\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }\left(1+h_{\nu }\right){\displaystyle {\int }_0^{T}E{\left|m_s\right|}^2\text{d}s}\\ ={\left(1+h_{\nu }\right)}^2{\left(1+T\right)}^{\frac{1}{2}}{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }{\displaystyle {\int }_0^T\left(1+s\right){\text{e}}^{-\frac{4}{3}\theta {\left(1+s\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }{\displaystyle {\int }_0^s{\text{e}}^{\frac{4}{3}\theta {\left(1+u\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }\text{d}u}\text{d}s}\\ ~{\left(1+T\right)}^2{\text{e}}^{-\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{4}{3}\theta }\end{array}$

可以得到

${\left(1+T\right)}^{\frac{1}{4}}{\text{e}}^{-\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}+\frac{2}{3}\theta }{\displaystyle {\int }_0^T{m}_s}\text{d}{L}_s\stackrel{L^2}{\to }0$

综上所述结合引理4.1，有

${\left(1+T\right)}^{-\frac{1}{4}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }\left({\hat{\theta }}_T-\theta \right)=\frac{{\left(1+T\right)}^{-\frac{1}{2}}{\text{e}}^{\frac{4}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{4}{3}\theta }}{{\displaystyle {\int }_0^T{Y}_t^2}\text{d}t}\frac{{\displaystyle {\int }_0^T{Y}_t}\text{d}{L}_t}{{\left(1+T\right)}^{-\frac{1}{4}}{\text{e}}^{\frac{2}{3}\theta {\left(1+T\right)}^{\frac{3}{2}}-\frac{2}{3}\theta }}\to \frac{2\theta L_1}{{\xi }_{\infty }}$

依分布收敛，其中 $L_1$ 服从无限可分分布，生成三元组为 $\left({\left(2\theta \right)}^{-\frac{1}{2}},K_T^{-1}\nu ,0\right)$ 并且 $L_1$ 和 ${\xi }_{\infty }$ 相互独立。定理得证。

NOTES

^*通讯作者。