基于统计复杂度下随机双稳态能量采集系统的随机共振

Stochastic Resonance of a Stochastic Bistable Energy Harvesting System Based on Statistical Complexity

摘要: 针对泊松白噪声和周期信号共同作用下双稳态能量采集系统，运用统计复杂度方法度量了系统的随机共振行为和采能效率。首先，通过数值方法计算了系统的统计复杂度和有效输出功率；其次，深入研究噪声、系统以及信号等参数对系统随机共振现象与采能效率的影响；最后，从信息论的角度解析了随机共振与系统采能效率之间的关系。结果显示，统计复杂度曲线的非单调演化趋势意味着系统产生了随机共振现象；选取合适的噪声强度、耦合系数及阻尼系数等能够增强系统的随机共振行为。此外，均方电压和有效输出功率曲线与统计复杂度曲线具有相同的演化规律，即当系统产生随机共振行为时，采能效率达到最大化。

Abstract: For the bistable energy harvesting system under the combined action of Poisson white noise and periodic signal, the statistical complexity method is used to measure the stochastic resonance behavior and energy recovery efficiency of the system. Firstly, the statistical complexity and effective output power of the system are calculated by numerical methods. Secondly, the influence of noise, system and signal parameters on the stochastic resonance phenomenon and energy recovery efficiency of the system is deeply studied. Finally, from the perspective of information theory, the relationship between stochastic resonance and the energy recovery efficiency of the system is analyzed. The results show that the non-monotonic evolution trend of the statistical complexity curve means that the system produces stochastic resonance. Selecting appropriate noise intensity, coupling coefficient and damping coefficient can enhance the stochastic resonance behavior of the system. In addition, the mean square voltage and effective output power curves have the same evolution law as the statistical complexity curve, that is, when the system produces random resonance behavior, the energy recovery efficiency is maximized.

1. 引言

当今社会，可再生能源的研究与开发已成为科技发展的热点领域。其中，振动能量采集系统作为一种新兴的能源回收技术，通过收集和转换机械振动能量，实现对环境中废弃能量的回收和再利用，具有广泛的应用前景 [1] [2] [3] 。振动能量采集系统可分为线性系统和非线性系统，非线性系统根据结构的不同又可分为单稳态和多稳态系统等。在实际应用过程中，非线性双稳态系统由于具有良好的稳定性，能够在较宽的频带范围内实现较大的振幅和能量输出，同时具有更强的能量转换效率等独特优势而成为学者们研究能量采集系统的重点方向 [4] [5] [6] 。如：王康 [7] 发现双稳态能量采集系统相对于单稳态具有更显著的非线性特性，同时明显提高了系统的电压输出。Liu等 [8] 针对系统参数对双稳态能量采集系统进行分析，发现系统参数的改变可以提高系统能量的输出功率。刘丽兰等 [9] 对双稳态能量采集系统的势阱深度进行分析，得出势阱深度的改变影响着系统发电性能的结论。李小亚 [10] 发现在合适的耦合系数下双稳态能量采集系统有较好的采集性能。Zhang等 [11] 发现通过给与外部联合激励，双稳态能量采集系统产生的功率比单一激励刺激下产生的功率高82.99%。这说明仅通过双稳态非线性结构还不足以适应环境中复杂多变的振动源，因此更多的学者考虑了噪声和周期信号等条件。

众所周知，在实际应用中，噪声是难以避免的，因此在双稳态能量采集系统中加入噪声因素可以模拟现实场景中的不确定性，使系统更加接近现实环境。而随机共振现象 [12] 是指噪声、周期激励和非线性系统之间的相互作用，使得其统计特征量在适量噪声强度下达到最优值的一种动力学跃迁现象。因此，将随机共振引入到能量采集系统中不仅能提高系统的效率和稳定性，还能更好地阐释参数对系统的动力学影响，并且大量学者取得了相关的研究成果。Zhao等 [13] 证实了通过随机共振可以提高双稳态能量采集系统的输出。Guo等 [14] 对双稳态振动能量采集系统进行分析，证实了随机共振的发生可以有效促进系统的发电性能。Zhao等 [15] 应用随机共振提升了双稳态能量采集系统的采能效率。此外，陈仲生等 [16] 发现利用随机共振可以将带有周期信号与随机激励的双稳态系统能量集中输出。肖少敏 [17] 在高斯白噪声激励下的双稳态能量采集系统中发现当随机共振现象发生时，系统的输出最高。Litak等 [18] 通过分析高斯白噪声和周期激励下双稳态能量采集系统，发现存在一个激发随机共振现象的最佳噪声强度。上述的研究成果大多基于高斯噪声所得，而高斯噪声是连续均匀分布的噪声，这在现实生活中不太符合噪声的特性。泊松白噪声是一种在现实生活环境中较为常见的噪声，它适用于描述稀疏事件，如星空中的流星、电话通话中的背景噪声等，故而研究泊松白噪声激励下的能量采集系统更具现实意义。

因此，本文采用统计复杂度方法探究泊松白噪声和周期信号共同作用下双稳态能量采集系统的随机共振机理，并利用均方电压和有效输出功率衡量系统的采能效率。首先，构建了非线性双稳态振动能量采集系统的数学模型。其次，通过数值模拟，分析了系统各个参数对统计复杂度、均方电压和有效输出功率的影响。最后，深入研究了随机共振与能量采集效率之间的关联性。

2. 双稳态振动能量采集系统

振动能量采集是一种利用振动信号转换为电能的技术。这种技术可以通过使用压电材料、电磁感应或机械共振等方式，将振动转化为电能 [19] ，其相应的数学模型为振动能量采集系统。现考虑一类质量为M、压电梁长度为L的压电振动能量采集系统 [20] ，同时受到噪声和周期信号的共同作用，其模型表示为：

$\{\begin{array}{l}M\ddot{\stackrel{¯}{X}}+B\stackrel{\dot{}}{\bar{X}}+\text{d}\bar{U}\left(\bar{X}\right)/\text{d}\bar{X}+\theta \bar{Y}=-M{\ddot{\stackrel{¯}{X}}}_a+M{\ddot{\stackrel{¯}{X}}}_b\\ Q\bar{Y}+\bar{Y}/R=\theta \stackrel{\dot{}}{\bar{X}},\end{array}$ (1)

式中 $\bar{X}$ 为系统的振动位移， $\bar{U}\left(\bar{X}\right)$ 为系统的势函数， $\bar{Y}$ 为压电感应电流， ${\ddot{\stackrel{¯}{X}}}_a$ 为泊松白噪声激励， ${\ddot{\stackrel{¯}{X}}}_b$ 为弱周期激励，B为线性阻尼系数， $\theta$ 为压电耦合系数，Q为压电元件的电容系数，R为相应的等效电阻负载。

进一步将模型中的物理量简化，引入如下变量和参数转化：

$X=\frac{\bar{X}}{L},V=\frac{Q}{L\theta }\bar{Y},\frac{\text{d}U\left(X\right)}{\text{d}X}=\frac{1}{ML}\frac{\text{d}\bar{U}\left(\bar{X}\right)}{\text{d}\bar{X}},c=\frac{B}{M},$

$\eta \left(t\right)=-\frac{{\ddot{\stackrel{¯}{X}}}_a}{L},A\cos \left(\omega t\right)=\frac{{\ddot{\stackrel{¯}{X}}}_b}{L},\kappa =\frac{{\theta }^2}{MQ},a=\frac{1}{QR},$

此时系统(1)可简化为：

$\{\begin{array}{l}\ddot{X}+c\stackrel{\dot{}}{X}+\frac{\text{d}U\left(X\right)}{\text{d}X}+\kappa V=\eta \left(t\right)+A\cos \left(\omega t\right)\\ \stackrel{\dot{}}{V}+aV=\stackrel{\dot{}}{X}\end{array}$ (2)

其中X为振动位移，V为感应电压，c为阻尼系数， $\kappa$ 为压电耦合系数，a为时间常数比， $U\left(X\right)$ 为系统的势函数， $A\cos \left(\omega t\right)$ 表示幅值为A、频率为 $\omega$ 的周期信号， $\eta \left(t\right)$ 为泊松白噪声。

泊松白噪声是一种随机脉冲序列的数学模型，当随机脉冲序列的有效作用时间远小于系统自由振动的时间，同时脉冲到达率为一个常数时，此序列即为泊松白噪声。数学上泊松白噪声 $\eta \left(t\right)$ 定义为复合泊松过程 $C\left(t\right)$ 的形式导数 [21] ：

$\eta \left(t\right)={\displaystyle \underset{k=1}{\overset{N\left(t\right)}{\sum }}{a}_k\delta \left(t-t_k\right)}\equiv \frac{\text{d}C\left(t\right)}{\text{d}t},C\left(t\right)={\displaystyle \underset{k=1}{\overset{N\left(t\right)}{\sum }}{a}_k}U\left(t-t_k\right)$ , (3)

式中， $\delta \left(t-t_k\right)$ 是狄拉克函数， $U\left(t\right)$ 是单位阶跃函数； $N\left(t\right)$ 是一个泊松计数过程，表征了在0到t时间间隔内脉冲平均到达率 $\lambda$ 时的脉冲个数， $a_k$ 代表了单个随机脉冲的强度，它与脉冲到达时间 $t_k$ 是相互独立的。不失普遍性，随机脉冲的振幅 $a_k$ 被假定为零均值且方差为 $\sigma$ 的高斯分布，泊松白噪声 $\eta \left(t\right)$ 的强度是 $\lambda {\sigma }^2$ 。

为了实现系统更复杂的能量传递和动态行为，考虑系统的势函数具有如下形式：

$U\left(X\right)=-\frac{1}{2}{X}^2+\frac{1}{4}{X}^4+\frac{1}{6}{X}^6$ (4)

此时稳定点为 $x_{s1}=\sqrt{\left(\sqrt{5}-1\right)/2}$ 、 $x_{s2}=-\sqrt{\left(\sqrt{5}-1\right)/2}$ ，不稳定点 $x_{un}=0$ ，且系统的势垒高度为 $\Delta U=\sqrt{10\sqrt{5}-22}$ 。将(4)式代入系统(2)，其对应的振动能量采集系统可化为如下形式：

$\{\begin{array}{l}\ddot{X}=-c\stackrel{\dot{}}{X}+X-X^3-X^5-\kappa V+\eta \left(t\right)+A\cos \left(\omega t\right)\\ \stackrel{\dot{}}{V}=-aV+\stackrel{\dot{}}{X}\end{array}$ (5)

为了评估该能量采集系统的采能效率，采用均方电压与有效输出功率 [22] 作为衡量指标，有效输出功率的表达式如下：

$P=\frac{E\left[V^2\right]}{R}$ (6)

其中 $E\left[V^2\right]$ 为均方电压，R为外部电阻。由此可见，均方电压和有效输出功率成正比例关系，与外部电阻成反比例关系，本文当中固定 $R=0.5$ 。

3. 统计复杂度

统计复杂度定义采用如下的泛函表达式 [23] ：

$C\left[P\right]=H\left[P\right]\cdot Q\left[P\right]$ , (7)

式中 $H\left[P\right]$ 表示标准Shannon熵 [24] ，用于描绘系统的无序性，定义如下：

$H\left[P\right]=S\left[P\right]/S_{\max }$ , (8)

$S\left[P\right]=-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{p}_i\ln \left(p_i\right)}$ , (9)

$S_{\max }=S\left[P_e\right]=\ln N$ ， $P_e=\left\{1/N,\cdots ,1/N\right\}$ 表示均匀分布。

$Q\left[P\right]$ 表示失衡度，其表达式为：

$Q\left[P\right]=Q_0\cdot D_s\left[P,P_e\right]$ , (10)

其中 $Q_0$ 为归一化常数， $D_s$ 表示这两个分布之间的距离。

4. 随机共振

在本节中，我们运用统计复杂度方法分析泊松白噪声和周期信号共同诱导下双稳态能量采集系统(5)的随机共振行为。首先，通过Bandt-pompe算法 [25] 生成响应系统驻留时间间隔序列对应的概率分布，进而计算出系统的统计复杂度与标准Shannon熵；接下来，进行数值模拟以得到系统的均方电压与有效输出功率；最后，探讨各个参数对统计复杂度和系统能量采集效率的影响。

4.1. 随机共振的产生

统计复杂度和标准Shannon熵作为噪声强度D函数的演化情况如图1所示，选取参数 $\lambda =1.5$ 、 $\kappa =0.6$ 、 $c=0.5$ 、 $A=1.2$ 、 $\omega =0.015$ 。图1(a)显示，随着噪声强度D增大，统计复杂度曲线先逐渐上升后下降。这表明，系统的复杂性在噪声强度增大到一定程度后逐渐减弱。图1(b)中，标准Shannon熵曲线在噪声强度D增大的过程中先降低后升高。这表明，系统在噪声作用下，演化行为从“无序”转变为“有序”，然后“有序性”又被破坏，逐渐呈现“无序性”。因此，统计复杂度和标准Shannon熵曲线的非单调性揭示了系统随机共振现象的发生。

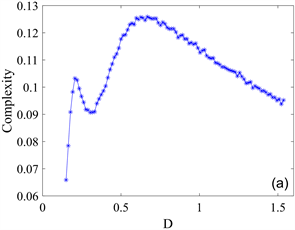
Figure 1. (a) Statistical complexity as a variation curve of Poisson white noise intensity D; (b) Standard Shannon entropy as a variation curve of Poisson white noise intensity D

图1. (a) 统计复杂度作为泊松白噪声强度D的变化曲线；(b) 标准Shannon熵作为泊松白噪声强度D的变化曲线

4.2. 泊松白噪声对系统随机共振和能量采集效率的影响

本小节研究泊松白噪声强度D、脉冲平均到达率λ对系统随机共振行为和采能效率的影响。考察统计复杂度和标准Shannon熵作为噪声强度D的函数随不同脉冲平均到达率λ的演化情形如图2所示，固定参数 $\kappa =0.6$ 、 $c=0.5$ 、 $A=1.2$ 、 $\omega =0.015$ 。从图中可以观测到，每条统计复杂度和标准Shannon熵曲线都呈现出非单调变化，表明系统产生了随机共振现象。另外，随着平均到达率λ从0.5增大到2.0时，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，并且输出峰值所对应的噪声强度值未发生改变，也就是说，选取较小的平均到达率可以增强系统的随机共振行为。

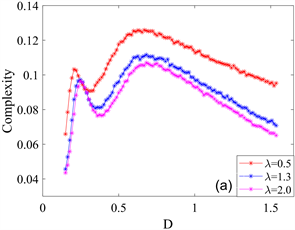
Figure 2. Evolution of statistical complexity and standard Shannon entropy with different average arrival rates λ. (a) Statistical complexity as the variation curve of Poisson white noise intensity D; (b) Standard Shannon entropy as the variation curve of Poisson white noise intensity D

图2. 统计复杂度和标准Shannon熵在不同平均到达率λ下的演化趋势。(a) 统计复杂度作为泊松白噪声强度D的变化曲线；(b) 标准Shannon熵作为泊松白噪声强度D的变化曲线

图3描绘了均方电压 $E\left[V^2\right]$ 和有效输出功率P作为泊松白噪声强度D的函数随不同平均到达率λ的演化情况，固定参数 $\kappa =0.6$ 、 $c=0.5$ 、 $A=1.2$ 、 $\omega =0.015$ 、 $R=0.5$ 。从图中可以看出，当噪声强度D逐步增大时，均方电压和有效输出功率曲线都出现了峰值，并且曲线的峰值随着平均到达率λ的减小而逐渐增大，这与图2(a)中统计复杂度曲线的演化趋势相一致，说明当系统发生随机共振时，此时系统的均方电压和有效输出功率达到最大值，这表明随机共振现象可以加强系统的采能效率。另外还可以发现，图3(a)与图3(b)有相同的演化趋势，这是由于两者之间只差系数1/R，由此也说明，选取较小的平均到达率并采用系统外部电阻值较小的电阻可以增强系统的随机共振行为，同时也可以促进系统的能量采集。

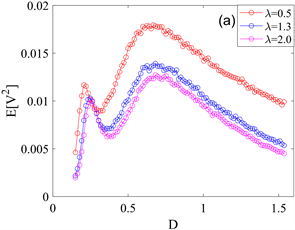
Figure 3. Evolutionary trends of mean-square voltage $E\left[V^2\right]$ and effective output power P under different average arrival rates λ. (a) Mean-square voltage $E\left[V^2\right]$ as a function of Poisson white noise intensity D; (b) Effective output power P as a function of Poisson white noise intensity D

图3. 均方电压 $E\left[V^2\right]$ 和有效输出功率P在不同平均到达率λ下的演化趋势。(a) 均方电压 $E\left[V^2\right]$ 作为泊松白噪声强度D的函数变化曲线；(b) 有效输出功率P作为泊松白噪声强度D的函数变化曲线

Figure 4. Effect of average arrival rate on system mean-square voltage and effective output power under Poisson white noise intensity D = 0.6. (a) Mean square voltage $E\left[V^2\right]$ as a function of average arrival rate λ; (b) Effective output power P as a function of average arrival rate λ

图4. 泊松白噪声强度D = 0.6下平均到达率对系统均方电压和有效输出功率的影响。(a) 均方电压 $E\left[V^2\right]$ 作为平均到达率λ的函数变化曲线；(b) 有效输出功率P作为平均到达率λ的函数变化曲线

图4给出了在噪声强度 $D=0.6$ 下均方电压 $E\left[V^2\right]$ 和有效输出功率P随平均到达率λ的函数的演化情况，固定其它参数 $\kappa =0.6$ 、 $c=0.5$ 、 $A=1.2$ 、 $\omega =0.015$ 、 $R=0.5$ 。可以观察到，对于给定的噪声强度 $D=0.6$ ，随着平均到达率λ从1增大至10，均方电压曲线和有效输出功率曲线都呈现出先逐渐减小继而趋于一个稳定值的变化趋势。这与图3所得结论保持一致，由此说明，脉冲平均到达率λ的减小会增强系统的随机共振现象，提升系统的能量采集效率。

4.3. 耦合系数对系统随机共振和能量采集效率的影响

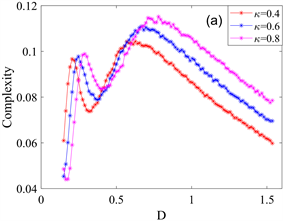
Figure 5. Evolution of statistical complexity and standard Shannon entropy with different coupling coefficients κ. (a) Statistical complexity as the variation curve of Poisson white noise intensity D; (b) Standard Shannon entropy as the variation curve of Poisson white noise intensity D

图5. 统计复杂度和标准Shannon熵在不同耦合系数κ下的演化趋势。(a) 统计复杂度作为泊松白噪声强度D的变化曲线；(b) 标准Shannon熵作为泊松白噪声强度D的变化曲线

Figure 6. Evolutionary trends of mean-square voltage $E\left[V^2\right]$ and effective output power P under different Poisson white noise intensities D. (a) Variation curve of mean-square voltage $E\left[V^2\right]$ with coupling coefficient κ; (b) Variation curve of effective output power P with coupling coefficient κ

图6. 均方电压 $E\left[V^2\right]$ 和有效输出功率P在不同泊松白噪声强度D下的演化趋势。(a) 均方电压 $E\left[V^2\right]$ 随耦合系数κ的变化曲线；(b) 有效输出功率P随耦合系数κ的变化曲线

本小节讨论泊松白噪声强度D和耦合系数 $\kappa$ 对系统随机共振和采能效率的影响。统计复杂度和标准Shannon熵随着系统耦合系数 $\kappa$ 变化的趋势如图5所示，固定其他参数为 $\lambda =1.5$ 、 $c=0.5$ 、 $A=1.2$ 、 $\omega =0.015$ 。由图5观察到，统计复杂度和标准Shannon熵的每条曲线都出现了峰值，即系统发生了随机共振现象。另外，随着耦合系数 $\kappa$ 从0.4变化到0.8，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，并且两者峰值位置沿着噪声强度D增大的方向偏移。换句话说，在一定的噪声强度范围内，选取较大的耦合系数可以强化随机共振现象的发生。

接下来分析泊松白噪声强度D和耦合系数 $\kappa$ 对系统采能效率的影响，结果如图6所示，固定参数 $\lambda =1.5$ 、 $c=0.5$ 、 $A=1.2$ 、 $\omega =0.015$ 。当限定噪声强度取值范围为 $D=0.5$ 至0.8时，每条均方电压曲线和有效输出功率曲线都出现了单调递增的变化，即均方电压值和有效输出功率值都随着耦合系数的增大而增大，这说明固定噪声强度下，耦合系数 $\kappa$ 的增大可以促进系统的能量采集效率。这与图5(a)统计复杂度在噪声强度 $D\ge 0.5$ 的范围下产生的演化结果保持一致。还可注意到，在同一耦合系数 $\kappa$ 下，较小的噪声强度更能产生较强的均方电压和有效输出功率，这表明在一定噪声强度范围内，选取较小的噪声强度更有利于系统随机共振现象的产生，从而进一步提升系统的采能效率。

4.4. 阻尼系数对系统随机共振和能量采集效率的影响

本小节讨论泊松白噪声强度D和阻尼系数c对系统随机共振和采能效率的影响。统计复杂度和标准Shannon熵随着系统阻尼系数c变化的趋势如图7所示，固定其他参数为 $\lambda =1.0$ 、 $\kappa =0.6$ 、 $A=1.0$ 、 $\omega =0.01$ 。由图7观察到，统计复杂度和标准Shannon熵的每条曲线都出现了峰值，即系统发生了随机共振现象。另外，随着阻尼系数c从0.4变化到0.6，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，并且两者峰值位置沿着噪声强度D增大的方向偏移。这说明，在特定的泊松白噪声强度下，选取合适的阻尼系数可以强化随机共振现象的发生。

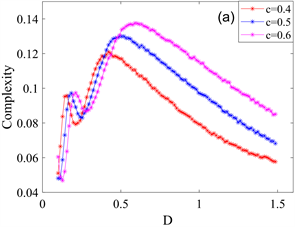
Figure 7. Evolution of statistical complexity and standard Shannon entropy with different damping coefficients c. (a) Variation curve of statistical complexity as a function of Poisson white noise intensity D; (b) Variation curve of standard Shannon entropy as a function of Poisson white noise intensity D

图7. 统计复杂度和标准Shannon熵在不同阻尼系数c下的演化趋势；(a) 统计复杂度作为泊松白噪声强度D的函数的变化曲线；(b) 标准Shannon熵作为泊松白噪声强度D的函数的变化曲线

阻尼系数c和泊松白噪声强度D对系统采能效率的影响如图8所示，固定其它参数 $\lambda =1.0$ 、 $\kappa =0.6$ 、 $A=1.0$ 、 $\omega =0.01$ 、 $R=0.5$ 。当泊松白噪声强度值为 $D=0.35$ 时，均方电压曲线和有效输出功率曲线都随着阻尼系数c的逐步增大出现了先增大后减小的趋势，即存在一个最优阻尼系数使得系统的有效输出功率达到最大化，这与图7所得到的结论相吻合。进一步表明，在特定的噪声强度下，选取合适的阻尼系数c可以更有利于系统随机共振现象的产生，从而达到提升系统采能效率的目的。

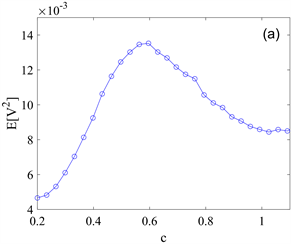
Figure 8. Effect of damping coefficient on system rms voltage and effective output power under Poisson white noise intensity $D=0.35$ . (a) Variation curve of rms voltage $E\left[V^2\right]$ as a function of damping coefficient c; (b) Variation curve of effective output power P as a function of damping coefficient c

图8. 泊松白噪声强度 $D=0.35$ 下阻尼系数对系统均方电压和有效输出功率的影响。(a) 均方电压 $E\left[V^2\right]$ 作为阻尼系数c的函数的变化曲线；(b) 有效输出功率P作为阻尼系数c的函数的变化曲线

4.5. 周期信号对系统随机共振和能量采集效率的影响

本小节继续分析周期信号幅值A和频率 $\omega$ 以及泊松白噪声强度D对系统随机共振和能量采集效率的影响。图9描述了统计复杂度与标准Shannon熵作为噪声强度D的函数随不同信号幅值A的变化曲线，给定参数 $\lambda =1.0$ 、 $\kappa =0.5$ 、 $c=0.5$ 、 $\omega =0.015$ 。可以发现，对于给定的信号幅值，随着噪声强度D的增大，每条统计复杂度曲线先增大后逐渐减小，标准Shannon熵曲线呈现出先减小后逐渐增大的趋势，说明系统产生了随机共振。另外，随着信号幅值A从0.8变化到1.4，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，并且两者峰值位置沿着噪声强度D增大的方向偏移。这说明，在一定的噪声强度范围内，较大信号幅值A更有利于强化系统的随机共振行为。

Figure 9. Evolution of statistical complexity and standard Shannon entropy with different signal amplitudes A. (a) Statistical complexity as the variation curve of Gaussian white noise intensity D; (b) Standard Shannon entropy as the variation curve of Gaussian white noise intensity D

图9. 统计复杂度和标准Shannon熵在不同信号幅值A下的演化趋势。(a) 统计复杂度作为高斯白噪声强度D的变化曲线；(b) 标准Shannon熵作为高斯白噪声强度D的变化曲线

为了比较泊松白噪声强度D对信号幅值A作用下系统能量采集效率的影响，图10讨论了均方电压 $E\left[V^2\right]$ 和有效输出功率P作为信号幅值A的函数在不同噪声强度D作用下的演化情形，固定参数 $\lambda =2.0$ 、 $\kappa =0.6$ 、 $c=0.5$ 、 $\omega =0.015$ 、 $R=0.5$ 。可以清晰地观察到，当限定噪声强度取值范围为 $D=0.4$ 至0.7时，每条均方电压曲线和有效输出功率曲线都出现了单调递增的变化，即均方电压值和有效输出功率值都随着信号幅值的增大而增大，这说明固定合适的噪声强度下，信号幅值A的增大可以加强系统的随机共振现象，促进系统的能量采集效率，这与图9(a)统计复杂度在噪声强度 $D\ge 0.4$ 的范围下产生的演化结果相吻合。还可注意到，在相同信号幅值A下，选用较小的噪声强度更有利于产生较强的均方电压和有效输出功率，这表明在一定噪声强度范围内，选取较小的噪声强度更有利于加强系统的随机共振现象，从而进一步提升系统的采能效率。

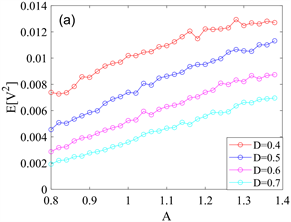
Figure 10. Evolution of mean-square voltage $E\left[V^2\right]$ and effective output power P under different Poisson white noise intensities D. (a) Variation curves of mean-square voltage $E\left[V^2\right]$ as a function of the amplitude of the periodic signal A; (b) Variation curves of effective output power P as a function of the amplitude of the periodic signal A

图10. 均方电压 $E\left[V^2\right]$ 和有效输出功率P在不同泊松白噪声强度D下的演化趋势。(a) 均方电压 $E\left[V^2\right]$ 作为周期信号幅值A的函数的变化曲线；(b) 有效输出功率P作为周期信号幅值A的函数的变化曲线

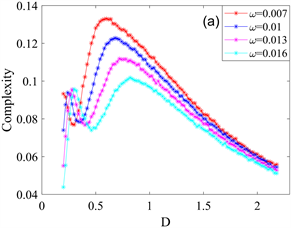
Figure 11. Evolution of statistical complexity and standard Shannon entropy at different signal frequencies ω. (a) Statistical complexity as a function of Poisson white noise intensity D; (b) Standard Shannon entropy as a function of Poisson white noise intensity D

图11. 统计复杂度和标准Shannon熵在不同信号频率ω下的演化趋势。(a) 统计复杂度作为泊松白噪声强度D的函数的变化曲线；(b) 标准Shannon熵作为泊松白噪声强度D的函数的变化曲线

接下来，进一步分析信号频率 $\omega$ 和泊松白噪声强度D对系统随机共振和能量采集效率的影响。图11给出了统计复杂度与标准Shannon熵作为噪声强度D的函数随不同信号频率 $\omega$ 的变化曲线，给定参数 $\lambda =2.0$ 、 $\kappa =0.6$ 、 $c=0.5$ 、 $A=1.2$ 。可以发现，对于给定的信号频率，随着噪声强度D的增大，每条统计复杂度曲线先增大后减小，标准Shannon熵曲线先减小后增大，说明系统产生了随机共振。另外，发现信号频率 $\omega$ 取值越小，统计复杂度曲线对应的峰值越大，标准Shannon熵曲线对应的峰值越小，且峰值的位置向噪声强度减小的方向发生偏移，表明较小的信号频率有助于系统随机共振现象的发生。

图12描述了在固定噪声强度 $D=0.6$ 下均方电压 $E\left[V^2\right]$ 和有效输出功率P作为信号频率 $\omega$ 的函数的演化情形，固定其它参数 $\lambda =2.0$ 、 $\kappa =0.6$ 、 $c=0.5$ 、 $\omega =0.015$ 、 $R=0.5$ 。可以明显地观测到，随着信号频率 $\omega$ 从0.006逐渐增大至0.016，系统的均方电压曲线和有效输出功率曲线都呈现出单调递减的变化，这与图11观察到的结果一致。这表明，较小的信号频率可以更有利于诱导系统产生随机共振现象，从而进一步提高系统的有效输出功率。

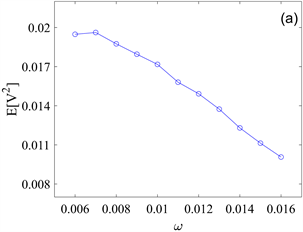
Figure 12. The effect of signal frequency on the mean square voltage and effective output power of the system at Poisson white noise intensity $D=0.6$ . (a) Mean square voltage $E\left[V^2\right]$ as a function of signal frequency ω; (b) Effective output power P as a function of signal frequency ω

图12. 泊松白噪声强度 $D=0.6$ 下信号频率对系统均方电压和有效输出功率的影响。(a) 均方电压 $E\left[V^2\right]$ 作为信号频率 $\omega$ 的函数的变化曲线；(b) 有效输出功率P作为信号频率ω的函数的变化曲线

5. 结论

本文针对泊松白噪声和弱周期信号共同驱动下双稳态能量采集系统，运用统计复杂度方法衡量了系统的随机共振行为，详细分析了系统参数、噪声强度以及信号参数对随机共振行为的影响，并用均方电压和有效输出功率等指标评估了系统能量采集的效率，进一步为提升相关领域系统的能量采集效率提供一个新的思路。

具体结果如下：

1) 统计复杂度和标准Shannon熵曲线呈现出非单调演化趋势，意味着随机共振现象的发生；当系统发生随机共振时，系统产生的均方电压和有效输出功率达到最大值，表明随机共振现象可以促进系统的能量采集效率。

2) 较大的平均到达率λ可使统计复杂度曲线的峰值以及均方电压和有效输出功率的值都逐渐减小并趋于一个稳定值，即平均到达率λ的增大可以削弱随机共振的强度，限制系统的采能效率。

3) 在一定的泊松白噪声强度下，选取合适的平均到达率λ、系统参数以及周期信号参数可使统计复杂度曲线峰值达到最大化，从而进一步增强随机共振现象，促进系统的能量采集。