基于统计复杂度下双稳态能量采集系统的随机共振分析

Stochastic Resonance Analysis of Bistable Energy Harvesting Systems Based on Statistical Complexity

摘要: 针对高斯白噪声和周期信号共同作用下双稳态能量采集系统，运用统计复杂度方法度量了系统的随机共振行为和采能效率。首先，借助数值方法计算了系统的统计复杂度和有效输出功率；其次，深入探究了噪声强度、耦合系数等参数对系统随机共振现象与采能效率的影响；最后，从信息论的角度阐释了随机共振与系统采能效率之间的作用规律。结果表明，统计复杂度曲线的非单调演化趋势意味着系统产生了随机共振现象；选取合适的噪声强度、耦合系数及阻尼系数等能够增强系统的随机共振行为。此外，均方电压和有效输出功率曲线与统计复杂度曲线具有相同的演化规律，即当系统产生随机共振行为时，采能效率达到最大化。

Abstract: Aiming at the bistable energy harvesting system under the joint action of Gaussian white noise and periodic signal, the statistical complexity method is applied to measure the stochastic resonance behavior and energy harvesting efficiency of the system. Firstly, the statistical complexity and effective output power of the system are calculated with the help of numerical methods; secondly, the effects of the noise intensity, coupling coefficient, and other parameters on the stochastic resonance phenomenon and energy harvesting efficiency of the system are investigated in depth; and lastly, the role of the stochastic resonance and the energy harvesting efficiency of the system is explained from the perspective of information theory. The results show that the non-monotonic evolution trend of the statistical complexity curve implies that the system generates a stochastic resonance phenomenon; the selection of appropriate noise intensity, coupling coefficient, and damping coefficient can enhance the stochastic resonance behavior of the system. In addition, the mean-square voltage and effective output power curves have the same evolution law as the statistical complexity curve, i.e., when the system generates stochastic resonance behavior, the energy harvesting efficiency is maximized.

1. 引言

振动能作为一种可再生能源，其回收利用已经引起了研究者们的广泛关注。振动能量采集系统 [1] [2] 通过将环境中的振动能源转化为电能，实现了能量的有效转化和利用。传统的线性系统结构简单，难以有效捕获环境中的振动源，因此近年来学者们开始研究非线性系统，以增强能量采集系统的复杂性和效率 [3] [4] 。一些研究表明，构建单稳态到多稳态等非线性结构以及给与周期激励的方式可以提高能量采集系统的性能。例如，刘迪等 [5] 人的研究证明了非对称单稳态能量采集系统能够产生高输出电压，并且在合适的非对称参数下具有良好的非线性特性。王康 [6] 发现双稳态能量采集系统相较于单稳态系统具有更显著的非线性特性，并且显著提高了系统的电压输出。Zhou等 [7] 对周期激励下三稳态能量采集系统进行研究，发现弱周期激励可以促进三稳态能量采集系统的采集性能。Lin等 [8] 分析了周期激励作用下三稳态能量采集系统高效率采能的条件，发现较大的振幅可以提高系统能量采集的效率。这些研究为振动能量采集系统的设计和优化提供了重要的理论基础，以推动振动能的可再生利用。

众所周知，噪声在自然环境中广泛存在，可以用来描述不同的振动环境，故而在能量采集系统中引入噪声具有一定的现实意义 [9] [10] [11] 。而随机共振现象 [12] 不仅可以描述噪声、周期激励和非线性系统之间的相互作用，还能更好地阐释参数对系统的动力学影响。因此，随机共振在振动能量采集系统中得到了广泛应用，并且取得了大量的研究成果。Zhao等 [13] 证实了通过随机共振可以提高双稳态能量采集系统的输出。Guo等 [14] 对双稳态压电振动能量采集系统进行分析，证实了随机共振的发生可以有效促进系统的发电性能。Zhao等 [15] 应用随机共振提升了双稳态能量采集系统的采能效率。此外，Zhang等 [16] 发现利用随机共振可以将带有周期信号与随机激励的双稳态系统能量集中输出。肖少敏 [17] 在高斯白噪声激励下的双稳态能量采集系统中发现当随机共振现象发生时，系统的输出最高。Litak等 [18] 通过分析高斯白噪声和周期激励下双稳态能量采集系统，发现存在一个激发随机共振现象的最佳噪声强度。以上研究结果表明，在振动能量采集系统中引入随机共振理论可以有效提高系统的能量采集效率和性能。

基于上述研究的基础上，本文从信息论的角度，采用统计复杂度方法探究高斯白噪声和弱周期信号共同作用下双稳态能量采集系统的随机共振机理，并利用均方电压和有效输出功率衡量系统的采能效率。首先，建立了非线性双稳态振动能量采集系统的数学模型；其次，基于数值模拟分析了系统各个参数对统计复杂度、均方电压和有效输出功率的影响；最后，进一步探讨了随机共振与能量采集效率之间的关联性。

2. 双稳态振动能量采集系统

压电振动能量采集器是一种将环境中的振动能量采集并转换成电能的微机电器件 [19] ，它利用压电陶瓷的正压电效应将环境中的能量收集，其相应的数学模型为压电振动能量采集系统。考虑一类质量为M、压电梁长度为L的压电振动能量采集系统 [20] ，同时受到噪声和周期信号的共同作用，其模型表示为：

$\{\begin{array}{l}M\ddot{\stackrel{¯}{X}}+B\stackrel{\dot{}}{\bar{X}}+\text{d}\bar{U}\left(\bar{X}\right)/\text{d}\bar{X}+\theta \bar{Y}=-M{\ddot{\stackrel{¯}{X}}}_a+M{\ddot{\stackrel{¯}{X}}}_b\\ Q\bar{Y}+\bar{Y}/R=\theta \stackrel{\dot{}}{\bar{X}},\end{array}$ (1)

式中 $\bar{X}$ 为系统的振动位移， $\bar{U}\left(\bar{X}\right)$ 为系统的势函数， $\bar{Y}$ 为压电感应电流， ${\ddot{\stackrel{¯}{X}}}_a$ 为噪声激励， ${\ddot{\stackrel{¯}{X}}}_b$ 为弱周期激励，B为线性阻尼系数， $\theta$ 为压电耦合系数，Q为压电元件的电容系数，R为相应的等效电阻负载。

为了将模型中的物理量进行简化，引入如下变量和参数转化：

$X=\frac{\bar{X}}{L},V=\frac{Q}{L\theta }\bar{Y},\frac{\text{d}U\left(X\right)}{\text{d}X}=\frac{1}{ML}\frac{\text{d}\bar{U}\left(\bar{X}\right)}{\text{d}\bar{X}},c=\frac{B}{M},$

$\xi \left(t\right)=-\frac{{\ddot{\stackrel{¯}{X}}}_a}{L},A\cos \left(\omega t\right)=\frac{{\ddot{\stackrel{¯}{X}}}_b}{L},\kappa =\frac{{\theta }^2}{MQ},a=\frac{1}{QR},$

此时系统(1)可简化为：

$\{\begin{array}{l}\ddot{X}+c\stackrel{\dot{}}{X}+\frac{\text{d}U\left(X\right)}{\text{d}X}+\kappa V=\xi \left(t\right)+A\text{cos}\left(\omega t\right)\\ \stackrel{\dot{}}{V}+aV=\stackrel{\dot{}}{X}\end{array}$ (2)

其中X为振动位移，V为感应电压，c为阻尼系数， $\kappa$ 为压电耦合系数，a为时间常数比， $U\left(X\right)$ 为系统的势函数， $A\cos \left(\omega t\right)$ 表示幅值为A、频率为 $\omega$ 的周期信号。 $\xi \left(t\right)$ 为高斯白噪声，其统计性质如下：

$\langle \xi \left(t\right)\rangle =0,\langle \xi \left(t\right)\xi \left(s\right)\rangle =2D\delta \left(t-s\right)$

式中 $\langle \cdot \rangle$ 表示数学期望，D是高斯白噪声强度， $\delta (\cdot )$ 是Dirac函数。

考虑系统的势函数具有如下形式：

$U\left(X\right)=-\frac{1}{2}{X}^2-\frac{1}{2}{X}^4+\frac{1}{6}{X}^6$ (3)

此时稳定点为 $x_{s1}=\sqrt{1+\sqrt{2}}$ 、 $x_{s2}=-\sqrt{1+\sqrt{2}}$ ，不稳定点 $x_{un}=0$ ，且系统的势垒高度为 $\Delta U=\frac{5+4\sqrt{2}}{6}$ 。将(3)式代入系统(2)，其对应的振动能量采集系统可化为如下形式：

$\{\begin{array}{l}\ddot{X}+c\stackrel{\dot{}}{X}-X-2X^3+X^5+\kappa V=\xi \left(t\right)+A\text{cos}\left(\omega t\right)\\ \stackrel{\dot{}}{V}+aV=\stackrel{\dot{}}{X}\end{array}$ (4)

为了刻画该能量采集系统的采能效率，采用均方电压与有效输出功率 [21] 作为衡量指标，有效输出功率的表达式如下：

$P=\frac{E\left[V^2\right]}{R}$ (5)

其中 $E\left[V^2\right]$ 为均方电压，R为外部电阻，可以看出，均方电压和有效输出功率成正比例关系。

3. 统计复杂度

统计复杂度定义采用如下的泛函表达式 [22] ，即：

$C\left[P\right]=H\left[P\right]\cdot Q\left[P\right]$ , (6)

式中 $H\left[P\right]$ 表示标准Shannon熵 [23] ，刻画系统的无序性，定义为：

$H\left[P\right]=S\left[P\right]/S_{\max }$ , (7)

$S\left[P\right]=-{\displaystyle \underset{i=1}{\overset{N}{\sum }}{p}_i\ln \left(p_i\right)}$ , (8)

$S_{\max }=S\left[P_e\right]=\ln N$ ， $P_e=\left\{1/N,\cdots ,1/N\right\}$ 表示均匀分布。

$Q\left[P\right]$ 表示失衡度，其表达式为：

$Q\left[P\right]=Q_0\cdot D_s\left[P,P_e\right]$ , (9)

其中 $Q_0$ 为归一化常数， $D_s$ 表示这两个分布之间的距离。

4. 随机共振

在这一节中，我们采用统计复杂度方法分析高斯白噪声和周期信号共同诱导下双稳态能量采集系(4)的随机共振行为。首先，通过Bandt-pompe算法 [24] 构造响应系统驻留时间间隔序列对应的概率分布，进而得到系统的统计复杂度与标准Shannon熵；其次，数值模拟得到系统的均方电压与有效输出功率；最后，讨论各个参数对统计复杂度与能量采集效率的影响。

4.1. 随机共振的产生

统计复杂度和标准Shannon熵作为噪声强度D的函数的演化情况如图1所示，其中选取参数 $\kappa =0.5$ 、 $c=0.05$ 、 $A=0.8$ 、 $\omega =0.02$ 。

Figure 1. (a) Variation curve of statistical complexity as the intensity D of Gaussian white noise; (b) Variation curve of standard Shannon entropy as the intensity D of Gaussian white noise

图1. (a) 统计复杂度作为高斯白噪声强度D的变化曲线；(b) 标准Shannon熵作为高斯白噪声强度D的变化曲线

从图1(a)中可以看出，随着噪声强度D的不断增大，统计复杂度曲线先逐渐地增大后减小。根据统计复杂度的定义可知，系统的复杂性随着噪声强度的增大逐渐地增强到某一最大程度后又逐渐地被削弱。在图1(b)中，标准Shannon曲线随着噪声强度D的增大先逐渐减小后增大。根据标准Shannon熵的定义可知，随着噪声强度的增大，系统的演化行为从“无序”结构到达了某一“有序”规则状态，之后系统的“有序性”被破坏又逐步显现出“无序性”，由此可知统计复杂度和标准Shannon熵曲线的非单调结构表明系统发生了随机共振现象。

4.2. 系统耦合系数对随机共振和能量采集效率的影响

本小节研究高斯白噪声强度D、耦合系数 $\kappa$ 对系统随机共振行为和采能效率的影响。考察统计复杂度和标准Shannon熵作为噪声强度D的函数随不同耦合系数 $\kappa$ 的演化情形如图2所示，固定参数 $A=0.8$ 、 $c=0.05$ 、 $\omega =0.02$ 。从图中可以观测到，每条统计复杂度和标准Shannon熵曲线都呈现出非单调变化，表明系统产生了随机共振现象。另外，随着耦合系数 $\kappa$ 从0.3变化到0.5时，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，并且输出峰值所对应的噪声强度值变得越来越大，也就是说，选取合适的耦合系数可以增强系统的随机共振行为。

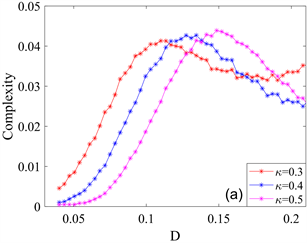
Figure 2. Variation curves of statistical complexity and standard Shannon entropy with the intensity D of Gaussian white noise for different coupling coefficients $\kappa$ . (a) Evolution of the statistical complexity with respect to the noise intensity D; (b) Evolution of the standard Shannon entropy with respect to the noise intensity D

图2. 不同耦合系数 $\kappa$ 作用下统计复杂度和标准Shannon熵随高斯白噪声强度D的变化曲线。(a) 统计复杂度关于噪声强度D的演化图；(b) 标准Shannon熵关于噪声强度D的演化图

图3描绘了均方电压 $E\left[V^2\right]$ 和有效输出功率P作为高斯白噪声强度D的函数随不同耦合系数 $\kappa$ 的演化情况，固定参数 $c=0.05$ 、 $\omega =0.02$ 、 $A=0.8$ ， $R=0.5$ 。从图中可以看出，当噪声强度D逐步增大时，均方电压和有效输出功率曲线都出现了峰值，并且曲线的峰值随着耦合系数 $\kappa$ 的增大而逐渐增大，这与图2(a)中统计复杂度曲线的演化趋势相一致，说明当系统发生随机共振时，此时均方电压和有效输出功率达到最大值。另外还可以发现，图3(a)与图3(b)有相同的演化趋势，这是由于两者之间只差系数1/R，由此也说明，选取合适的耦合系数可以增强系统的随机共振行为，同时也可以促进系统的能量采集。

为了进一步探究高斯白噪声强度D和耦合系数 $\kappa$ 对系统随机共振的影响，图4给出了不同噪声强度下，统计复杂度和标准Shannon熵随系统耦合系数 $\kappa$ 的变化曲线，固定参数 $A=0.8$ 、 $c=0.05$ 、 $\omega =0.02$ 、 $R=0.5$ 。从图中可以观察到，在噪声强度 $D=0.12$ 、 $D=0.13$ 、 $D=0.14$ 的条件下，每条统计复杂度曲线都随着耦合系数 $\kappa$ 的增大呈现出先增大后减小的趋势，每条标准Shannon熵曲线随着耦合系数 $\kappa$ 的增大呈现出先减小后增大的趋势，说明选取合适的耦合系数 $\kappa$ 可加强系统的随机共振，这与图2所对应的结果保持一致。又注意到，随着噪声强度D的增大，统计复杂度曲线所对应的峰值也相应地增大，而标准Shannon熵曲线所对应的峰值相应地减小，这表明较大的噪声强度D有利于系统随机共振现象的产生。

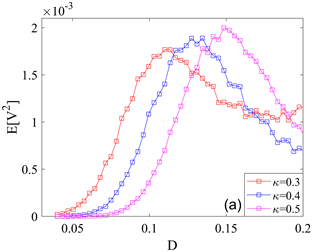
Figure 3. Variation curves of mean square voltage $E\left[V^2\right]$ and effective output power P with Gaussian white noise intensity D for different coupling coefficients $\kappa$ . (a) Evolution of mean square voltage $E\left[V^2\right]$ with respect to noise intensity D; (b) Evolution of the effective output power P with respect to the noise intensity D

图3. 不同耦合系数 $\kappa$ 作用下均方电压 $E\left[V^2\right]$ 和有效输出功率P随高斯白噪声强度D的变化曲线。(a) 均方电压 $E\left[V^2\right]$ 关于噪声强度D的演化图；(b) 有效输出功率P关于噪声强度D的演化图

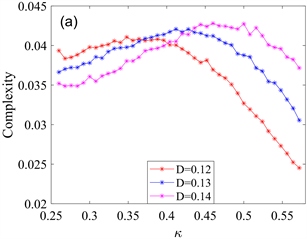
Figure 4. Evolution of statistical complexity and standard Shannon entropy as a function of coupling coefficient $\kappa$ for different noise intensities D. (a) Evolution of the statistical complexity with respect to the coupling coefficient $\kappa$ ; (b) Evolution of the standard Shannon entropy with respect to the coupling coefficient $\kappa$

图4. 不同噪声强度D作用下统计复杂度和标准Shannon熵作为耦合系数 $\kappa$ 的函数演化情况。(a) 统计复杂度关于耦合系数 $\kappa$ 的演化图；(b) 标准Shannon熵关于耦合系数 $\kappa$ 的演化图

接下来，进一步分析高斯白噪声强度D和耦合系数 $\kappa$ 对系统采能效率的影响。图5给出了不同噪声强度下，均方电压 $E\left[V^2\right]$ 和有效输出功率P随系统耦合系数 $\kappa$ 的变化曲线，固定参数 $A=0.8$ 、 $c=0.05$ 、 $\omega =0.02$ 、 $R=0.5$ 。从图中可以得到，在噪声强度 $D=0.12$ 、 $D=0.13$ 、 $D=0.14$ 的条件下，均方电压 $E\left[V^2\right]$ 和有效输出功率P都随着耦合系数 $\kappa$ 的增大先增大后减小，即存在最大值，说明选取合适的耦合系数 $\kappa$ 可使系统输出功率达到最高，这与图3所得结论相吻合。除此之外还可发现，随着噪声强度D从0.12增大至0.14，均方电压曲线和有效输出功率曲线所对应的峰值也逐步增大，这表明较大的噪声强度D有利于系统的能量采集。

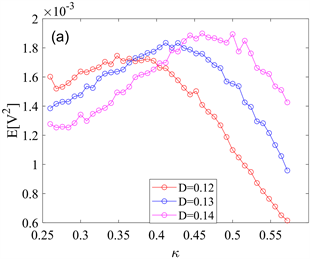
Figure 5. Evolution of the mean square voltage $E\left[V^2\right]$ and effective output power P as a function of the coupling coefficient $\kappa$ for different noise intensities D. (a) Evolution of the mean square voltage $E\left[V^2\right]$ with respect to the coupling coefficient $\kappa$ ; (b) Evolution of the effective output power P with respect to the coupling coefficient $\kappa$

图5. 不同噪声强度D作用下均方电压 $E\left[V^2\right]$ 和有效输出功率P作为耦合系数 $\kappa$ 的函数演化情况。(a) 均方电压 $E\left[V^2\right]$ 关于耦合系数 $\kappa$ 的演化图；(b) 有效输出功率P关于耦合系数 $\kappa$ 的演化图

4.3. 系统阻尼系数对随机共振和能量采集效率的影响

本小节讨论高斯白噪声强度D和阻尼系数c对系统随机共振和采能效率的影响。统计复杂度和标准Shannon熵随着系统阻尼系数c变化的趋势如图6所示，固定其他参数为 $A=0.8$ 、 $\kappa =0.5$ 、 $\omega =0.02$ 。由图6观察到，统计复杂度和标准Shannon熵的每条曲线都出现了峰值，即系统发生了随机共振现象。另外，随着阻尼系数c从0.02变化到0.05，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，并且两者峰值位置沿着噪声强度D增大的方向偏移。换句话说，选取合适的阻尼系数可以强化随机共振现象的发生。

图7给出了均方电压 $E\left[V^2\right]$ 和有效输出功率P作为高斯白噪声强度D的函数随不同阻尼系数c的演化情况，固定参数 $\kappa =0.5$ 、 $\omega =0.02$ 、 $A=0.8$ ， $R=0.5$ 。从图中可以看出，当噪声强度D逐步增大时，均方电压和有效输出功率曲线都出现了峰值，并且曲线的峰值随着阻尼系数c的增大而逐渐增大，这与图6(a)中统计复杂度曲线的演化趋势相一致，说明当系统发生随机共振时，此时均方电压和有效输出功率达到最大值。另外还可以发现，图7(a)与图7(b)有相同的演化趋势，由此也说明，选取合适的阻尼系数不仅可以增强系统的随机共振行为，同时还能提升系统的采能效率。

Figure 6. Variation curves of statistical complexity and standard Shannon entropy with Gaussian white noise intensity D for different damping coefficients c. (a) Evolution of statistical complexity with respect to the noise intensity D; (b) Evolution of the standard Shannon entropy with respect to the noise intensity D

图6. 不同阻尼系数c作用下统计复杂度和标准Shannon熵随高斯白噪声强度D的变化曲线。(a) 统计复杂度关于噪声强度D的演化图；(b) 标准Shannon熵关于噪声强度D的演化图

Figure 7. Variation curves of mean square voltage $E\left[V^2\right]$ and effective output power P with Gaussian white noise intensity D for different damping coefficients c. (a) Evolution of the mean square voltage $E\left[V^2\right]$ with respect to the noise intensity D; (b) Evolution of the effective output power P with respect to the noise intensity D

图7. 不同阻尼系数c作用下均方电压 $E\left[V^2\right]$ 和有效输出功率P随高斯白噪声强度D的变化曲线。(a) 均方电压 $E\left[V^2\right]$ 关于噪声强度D的演化图；(b) 有效输出功率P关于噪声强度D的演化图

为了进一步探究高斯白噪声强度D和阻尼系数c对系统随机共振的影响，图8描述了不同噪声强度下，统计复杂度和标准Shannon熵随系统阻尼系数c的变化曲线，固定参数 $A=0.8$ 、 $\kappa =0.5$ 、 $\omega =0.02$ 、 $R=0.5$ 。从图中可以观察到，在噪声强度 $D=0.12$ 、 $D=0.13$ 、 $D=0.14$ 的条件下，每条统计复杂度曲线都随着阻尼系数c的增大呈现出先增大后减小的趋势，每条标准Shannon熵曲线随着阻尼系数c的增大呈现出先减小后增大的趋势，说明选取合适的阻尼系数c可加强系统的随机共振，这与图6所对应的结果保持一致。又注意到，随着噪声强度D的增大，统计复杂度曲线所对应的峰值也相应地增大，而标准Shannon熵曲线所对应的峰值相应地减小，这表明较大的噪声强度D有利于系统随机共振现象的产生。

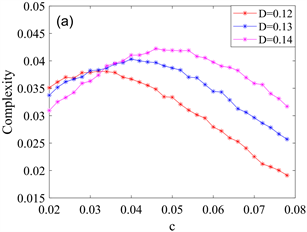
Figure 8. Variation curves of statistical complexity and standard Shannon entropy with damping coefficient c for different noise intensities D. (a) Evolution of the statistical complexity with respect to the damping coefficient c; (b) Evolution of the standard Shannon entropy with respect to the damping coefficient c

图8. 不同噪声强度D作用下统计复杂度和标准Shannon熵随阻尼系数c的变化曲线。(a) 统计复杂度关于阻尼系数c的演化图；(b) 标准Shannon熵关于阻尼系数c的演化图

接下来，进一步分析高斯白噪声强度D和阻尼系数c对系统能量采集效率的影响。图9给出了不同噪声强度下，均方电压 $E\left[V^2\right]$ 和有效输出功率P随系统阻尼系数c的变化曲线，固定参数 $A=0.8$ 、 $\kappa =0.5$ 、 $\omega =0.02$ 、 $R=0.5$ 。清晰地看到，对于特定的噪声强度 $D=0.12$ 、 $D=0.13$ 、 $D=0.14$ 下，均方电压曲线和有效输出功率曲线的演化趋势都随着阻尼系数c的增大呈现出先增大后减小的变化，即存在最大值。说明选取合适的阻尼系数c可使系统输出功率最大化，这与图7所得结论相吻合。另外还可注意到，随着噪声强度D从0.12增大至0.14，均方电压曲线和有效输出功率曲线所对应的峰值也逐步增大，这表明较大的噪声强度D可以提高系统的能量采集效率。

Figure 9. Variation curves of mean square voltage $E\left[V^2\right]$ and effective output power P with damping coefficient c for different noise intensity D. (a) Evolution of the mean square voltage $E\left[V^2\right]$ with respect to the damping coefficient c; (b) Evolution of the effective output power P with respect to the damping coefficient c

图9. 不同噪声强度D作用下均方电压 $E\left[V^2\right]$ 和有效输出功率P随阻尼系数c的变化曲线。(a) 均方电压 $E\left[V^2\right]$ 关于阻尼系数c的演化图；(b) 有效输出功率P关于阻尼系数c的演化图

4.4. 周期信号对随机共振和能量采集效率的影响

本小节继续分析周期信号频率 $\omega$ 和幅值A对系统随机共振和能量采集效率的影响。图10描述了统计复杂度与标准Shannon熵作为噪声强度D的函数随不同信号频率 $\omega$ 的变化曲线，给定参数 $\kappa =0.5$ 、 $c=0.05$ 、 $A=0.8$ 。可以发现，对于给定的信号频率，随着噪声强度D的增大，每条统计复杂度曲线先增大后减小，标准Shannon熵曲线先减小后增大，说明系统产生了随机共振。另外，发现信号频率 $\omega$ 越小，统计复杂度曲线的峰值越大，标准Shannon熵曲线的峰值越小，且峰值的位置向噪声强度减小的方向发生偏移，表明较小的信号频率有助于系统随机共振现象的发生。并且当噪声强度 $D=0.08$ 时， $\omega =0.008$ 的曲线峰值最大，说明此时系统随机共振行为较强。

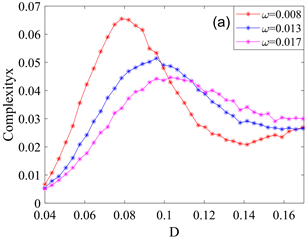
Figure 10. Variation curves of statistical complexity and standard Shannon entropy with Gaussian white noise intensity D for different periodic signal frequencies $\omega$ . (a) Evolution of statistical complexity with respect to the noise intensity D; (b) Evolution of standard Shannon entropy with respect to noise intensity D

图10. 不同周期信号频率 $\omega$ 作用下统计复杂度和标准Shannon熵随高斯白噪声强度D的变化曲线。(a) 统计复杂度关于噪声强度D的演化图；(b) 标准Shannon熵关于噪声强度D的演化图

图11描绘了均方电压 $E\left[V^2\right]$ 和有效输出功率P作为高斯白噪声强度D的函数随不同周期信号频率 $\omega$ 的演化图，固定参数 $\kappa =0.5$ 、 $c=0.05$ 、 $A=0.8$ ， $R=0.5$ 。可以由图11(a)看出，当噪声强度D从0.04逐步增加到0.16时，均方电压曲线都出现了峰值，并且曲线的峰值随着信号频率 $\omega$ 的减小而增大，这与图10(a)统计复杂度随噪声强度D和信号频率 $\omega$ 的演化趋势一致。另外，根据图10结论和图11可知，当噪声强度 $D=0.08$ 、信号频率 $\omega =0.008$ 时，此时系统发生了随机共振，且均方电压达到最大值，这说明随机共振行为可以提升系统的输出电压。另一方面，有效输出功率P随噪声强度D的变化如图11(b)所示，其保持图11(a)的演化行为，进一步表明较小的信号频率可以促进系统的能量采集。

接下来，进一步讨论统计复杂度和标准Shannon熵作为噪声强度D的函数随不同周期信号幅值A的演化情形。图12(a)中的统计复杂度曲线均存在最大值，图12(b)中的标准Shannon熵曲线均存在最小值，这意味着系统出现了随机共振现象。另外，给定参数 $\kappa =0.5$ 、 $c=0.05$ 、 $\omega =0.02$ ，随着振幅A的增大，统计复杂度曲线的峰值逐渐增大，标准Shannon熵曲线的峰值逐渐减小，这说明振幅的增大可以加强系统的随机共振现象。除此之外还可注意到，对于给定的振幅A，统计复杂度曲线和Shannon曲线的峰值都在噪声强度 $D=0.15$ 时取得，表明此时系统随机共振现象较强。

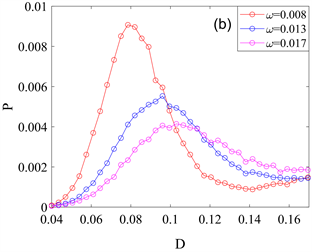
Figure 11. Variation curves of mean square voltage $E\left[V^2\right]$ and effective output power P with Gaussian white noise intensity D for different periodic signal frequencies $\omega$ . (a) Evolution of the mean square voltage $E\left[V^2\right]$ with respect to the noise intensity D; (b) Evolution of the effective output power P with respect to the noise intensity D

图11. 不同周期信号频率 $\omega$ 作用下均方电压 $E\left[V^2\right]$ 与有效输出功率P随高斯白噪声强度D的变化曲线。(a) 均方电压 $E\left[V^2\right]$ 关于噪声强度D的演化图；(b) 有效输出功率P关于噪声强度D的演化图

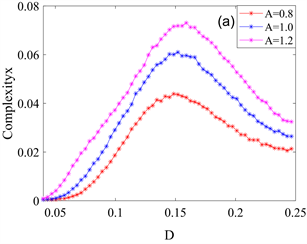
Figure 12. Variation curves of statistical complexity and standard Shannon entropy with Gaussian white noise intensity D for different periodic signal amplitudes A. (a) Evolution of the statistical complexity with respect to the noise intensity D; (b) Evolution of standard Shannon entropy with respect to noise intensity D

图12. 不同周期信号幅值A作用下统计复杂度和标准Shannon熵随高斯白噪声强度D的变化曲线。(a) 统计复杂度关于噪声强度D的演化图；(b) 标准Shannon熵关于噪声强度D的演化图

图13给出了在不同周期信号振幅A作用下均方电压 $E\left[V^2\right]$ 和有效输出功率P作为噪声强度D的函数的演化情况。固定参数 $\kappa =0.5$ 、 $c=0.05$ 、 $\omega =0.02$ 、 $R=0.5$ ，可以观察到，对于给定的振幅A，均方电压 $E\left[V^2\right]$ 和有效输出功率P都随着噪声强度D的增大呈现出先增大后减小的趋势，并且当 $D=0.15$ 时，均方电压 $E\left[V^2\right]$ 和有效输出功率P取得最大值，这和图12在 $D=0.15$ 处统计复杂度曲线的演化情况相吻合，更加说明周期信号振幅的增大有利于系统的能量采集。

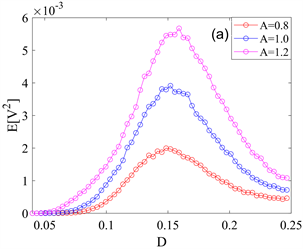
Figure 13. Variation curves of mean square voltage $E\left[V^2\right]$ and effective output power P with Gaussian white noise intensity D for different periodic signal amplitudes A. (a) Evolution of the mean square voltage $E\left[V^2\right]$ with respect to the noise intensity D; (b) Evolution of the effective output power P with respect to the noise intensity D

图13. 不同周期信号振幅A作用下均方电压 $E\left[V^2\right]$ 和有效输出功率P随高斯白噪声强度D的变化曲线。(a) 均方电压 $E\left[V^2\right]$ 关于噪声强度D的演化图；(b) 有效输出功率P关于噪声强度D的演化图

5. 结论

本文针对高斯白噪声和弱周期信号共同驱动下双稳态能量采集系统，采用统计复杂度方法度量了系统的随机共振行为，详细地分析了系统参数、噪声强度以及信号参数对系统随机共振行为的影响，并用均方电压和有效输出功率等指标衡量了系统能量采集的效率。

数值结果表明：统计复杂度和标准Shannon熵曲线呈现出非单调演化趋势，意味着系统随机共振现象的发生；当系统发生随机共振时，系统产生的均方电压和有效输出功率达到最大值，此时系统的能量采集效率是最优的。另外，当系统其它参数固定时，随着周期信号振幅A的增大或频率 $\omega$ 的减小，统计复杂度曲线的峰值增大意味着促进了系统随机共振现象的发生，同时均方电压和有效输出功率都得到了有效地提升，提高了系统能量采集效率，但需注意A和 $\omega$ 的取值范围；而在特定的高斯白噪声强度 $D=0.12$ 、 $D=0.13$ 、 $D=0.14$ 下，均方电压和有效输出功率的演化曲线都随着耦合系数 $\kappa$ 和阻尼系数c的增大而存在最大值，且其峰值随着噪声强度D的增大也相应地变大。因此，较大的高斯白噪声可以促进系统随机共振的发生并且选取合适的耦合系数和阻尼系数可以使系统随机共振现象呈现最大化，进一步提升系统的采能效率。