基于似然比扫描方法的INGARCH模型变点探测

Change Point Detection of INGARCH Models Based on Likelihood Ratio Scanning Method

摘要: 整数值时间序列数据在许多领域中非常常见，可用整数值广义自回归条件异方差(INGARCH)模型来拟合。本文研究了INGARCH模型中的变点探测问题，基于似然比扫描方法(LRSM)，讨论了分段平稳的INGARCH模型中变点的数量和位置。然后通过大量数值模拟，验证LRSM的有效性，最后并将其应用于实际数据的分析中。

Abstract: Integer-valued time series data are very common in many fields and can be fitted by integer-valued generalized autoregressive conditional heteroscedasticity (INGARCH) models. In this paper, the problem of change point detection in INGARCH model is studied. Based on the likelihood ratio scanning method (LRSM), the number and location of change points in piecewise stationary INGARCH process are discussed. Then the validity of LRSM is verified by a large number of numerical simulations, and finally it is applied to the analysis of real data.

1. 引言

近几十年来，变点探测问题一直是统计学中的一个热门话题。如今它不仅被广泛应用于工业质量控制 [1] ，还被广泛应用于经济 [2] 、金融 [3] 、医学 [4] 等领域。许多学者对变点探测问题进行了研究。例如，Picard [5] 研究了自回归AR模型变点的最大似然估计。Bai [6] 对最小二乘估计线性回归模型的多变点问题进行了深入探索。Kokoszka和Leipus [7] 研究了自回归条件异方差(ARCH)模型中单变点检测的相关问题。Liu [8] 提出了一个新的经验似然比统计量来检验无变点的零假设。Foygel和Drton [9] 基于群LASSO法，解决了数据稀疏条件下线性回归模型的变点问题。Hudecová，Hušková和Meintanis [10] 研究了INARCH模型中的变点探测问题。Chen和Lee [11] [12] 提出了一种贝叶斯方法来检测广义泊松INGARCH模型中的变点。Pein和Sieling [13] 提出了一种H-SMUCE的统计量，用于检测异质高斯回归模型中信号的多个变点问题。Lee [14] 利用支持向量回归(SVR)-自回归移动平均(ARMA)模型获得的残差，考虑了基于位置和尺度的CUSUM检验的时间序列变点检验问题。Lee和Kim [15] 重点介绍了整数值自回归(INAR)和INGARCH模型的CUSUM检验和整数值时间序列模型变点检验的最新进展。

在时间维度上，计数过程体现在生产生活各方面，比如一个城市在数月内道路交通事故发生次数、一家医院某种传染疾病每天的感染人数、商场中销售的某个商品数量、某只股票每天价格变动的次数、某一地区的犯罪数量和某个国家新增的失业人数等等。取值非负整数和有一定的自相关性是这种数据的两个明显的特点。而对于这类数据，如果用广义自回归条件异方差模型(GARCH)来拟合，效果不好。虽然这个模型可用来拟合有自相关关系的数据，但这个模型是在实数域基础上而非整数域，故对于这种数据，用整数值时间序列模型进行拟合要更好一些。近三十年来，许多整数值时间序列模型应时而生，其应用前景也越来越广阔。比如为描述癫痫患者的发作次数，Franke和Seligmann [16] 提出自激励门限自回归模型、Gauthier和Latour [17] 提出的广义整数值自回归模型等等。本文研究的整数值时间序列模型分别是由Ferland [18] 提出的泊松INGARCH模型，Fokianos和Tjøstheim [19] 提出对数线性泊松INGARCH模型。

变点探测常用的方法是通过优化特定的目标函数来寻找变点，如最小二乘法 [20] 和贝叶斯方法 [21] 。为了避免优化问题，BS方法 [22] 是一种流行的解决方案。此外，还有Davis等人 [23] 提出的遗传算法、Killic等人 [24] 提出的Pruned Exact Linear Time (PELT)方法和Yau等人 [25] 提出的LRSM。相比较于BS和PELT，LRSM不仅将计算难度从n²降低到 $\log \left(n\right)$ ，且提高了变点估计的准确性。目前，据我们所知，LRSM还没有运用到整数值时间序列的变点探测中。

本文的梗概如下。第2节中，我们将详细介绍基于LRSM在分段平稳过程中估计多个变点的三个步骤。第3节讨论了窗口半径的选取问题。第4节对LRSM进行了大量的模拟研究。通过对不同模型的重复试验，深入研究了LRSM的变点探测性能。第5节研究了LRSM在实际生活中的应用。第6节为对全篇内容做出总结，概述本论文所做的工作。

2. INGARCH模型以及似然比扫描方法

2.1. 泊松INGARCH模型

拟合整数值时间序列，其中最为经典的就是用Ferland等(2006) [18] 提出的泊松INGARCH模型来拟合，其定义如下：一个整数值过程 ${\left\{X_t\right\}}_{t\in \mathbb{Z}}$ ，满足

$\{\begin{array}{l}{X}_t|{\mathcal{F}}_{t-1}:\mathcal{P}\left({\lambda }_t\right)\forall t\in \mathbb{Z},\hfill \\ {\lambda }_t={\gamma }_0+{\displaystyle \underset{i=1}{\overset{q}{\sum }}{\gamma }_i}{X}_{t-i}+{\displaystyle \underset{j=1}{\overset{p}{\sum }}{\delta }_j}{\lambda }_{t-j},\hfill \end{array}$ (1)

其中， $\mathbb{Z}$ 是正整数域， ${\gamma }_0>0$ ， ${\gamma }_i\ge 0$ ， $i=1,\cdots ,q$ ， ${\delta }_j\ge 0$ ， $j=1,\cdots ,p$ ， ${\mathcal{F}}_{t-1}$ 表示由 $\left\{X_1,\cdots ,X_{t-1}\right\}$ 生成的 $\sigma$ 域， $\mathcal{P}\left({\lambda }_t\right)$ 表示均值为 ${\lambda }_t$ 的泊松分布。

为了简单起见，本节主要考虑泊松INGARCH (1, 1)模型的变点探测。

泊松INGARCH (1, 1)模型为

$\{\begin{array}{l}{X}_t|{\mathcal{F}}_{t-1}:\mathcal{P}\left({\lambda }_t\right)\forall t\in \mathbb{Z},\hfill \\ {\lambda }_t={\gamma }_0+{\gamma }_1{X}_{t-1}+{\delta }_1{\lambda }_{t-1},\hfill \end{array}$ (2)

关于该模型的统计性质有

1) 当 ${\gamma }_1+{\delta }_1<1$ 时，该模型是严平稳的。

2) 该过程的期望值为 $\begin{array}{c}E\left(X_t\right)=\frac{{\gamma }_0}{1-\left({\gamma }_1+{\delta }_1\right)}\end{array}$ 。

3) 该过程的方差为 $Var\begin{array}{c}\left(X_t\right)=\frac{\mu \left(1-{\left({\gamma }_1+{\delta }_1\right)}^2+{\gamma }_1^2\right)}{1-{\left({\gamma }_1+{\delta }_1\right)}^2}\end{array}$ 。

2.2. 似然比扫描方法

LRSM相较于其它变点探测方法，能够快速有效的探测出时间序列中的变点。本节详细介绍此方法的三个步骤。具体LRSM变点探测步骤如下：

步骤1：扫描观测序列 ${\left\{X_t\right\}}_{t=1,\cdots ,n}$ ，获得初始变点估计 ${\hat{\mathcal{J}}}^{\left(1\right)}$ ；

步骤2：结合最小描述长度准则(MDL)，得到一致变点估计 ${\hat{\mathcal{J}}}^{\left(2\right)}$ ；

步骤3：获得最终的变点估计 ${\hat{\mathcal{J}}}^{\left(3\right)}$ 。

具体变点探测问题流程图如图1所示。

本节详细介绍分段平稳的泊松INGARCH模型中的变点探测和估计问题。假设观测值 ${\left\{X_t\right\}}_{t=1,\cdots ,n}$ 来自于 $m+1$ 段平稳的泊松INGARCH过程，则第j段泊松INGARCH的表达式为：

$\begin{array}{cc}{Y}_{t,j}=X_t,& {\tau }_{j-1}\end{array}<t\le {\tau }_j,$ (3)

其中 $j=1,\cdots ,m$ ， ${\tau }_j$ 是泊松INGARCH (1, 1)过程的第j个变点，令 ${\tau }_0=1$ ， ${\tau }_{m+1}=n$ ， $\left\{Y_{t,j}\right\}$ 是平稳的泊松INGARCH (1, 1)过程，满足

$\{\begin{array}{l}{Y}_{t,j}|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_{t,j}\right)\forall t\in \mathbb{Z},\hfill \\ {\lambda }_{t,j}={\gamma }_{j,0}+{\gamma }_{j,1}{Y}_{t-1,j}+{\delta }_{j,1}{\lambda }_{t-1,j},\hfill \end{array}$ (4)

其中 ${\gamma }_{j,0}>0$ ， ${\gamma }_{j,1}\ge 0$ ， ${\delta }_{j,1}\ge 0$ ， ${\gamma }_{j,1}+{\delta }_{j,1}<1$ 。记 $\mathcal{J}=\left({\tau }_1,\cdots ,{\tau }_m\right)$ 为变点集合，定义 ${\tau }_j=\left[{\varpi }_{j}n\right]$ ， $j=1,\cdots ,m+1$ ， ${\varpi }_j\in \left[0,1\right]$ 是第j个变点的相对位置，对于 ${\epsilon }_{\varpi }>0$ ，有 ${\min }_{j=0,\cdots ,m}\left({\varpi }_{j+1}-{\varpi }_j\right)>{\epsilon }_{\varpi }$ 。下面对基于LRSM探测分段平稳的泊松INGARCH过程中变点的三个步骤进行详细介绍。

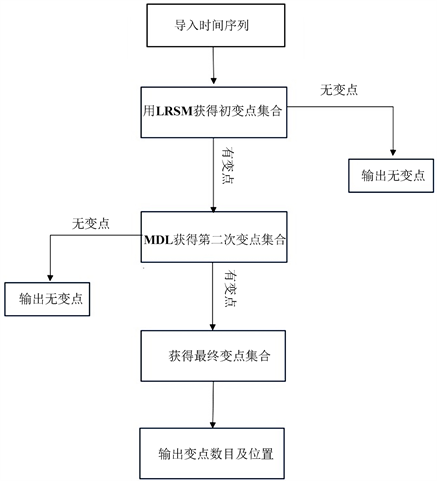
Figure 1. The flowchart depicts the procedure for detecting change points in a piecewise stationary autoregressive process

图1. 分段平稳自回归过程变点探测流程图

第一步：扫描来自于分段平稳泊松INGARCH过程的观测序列 ${\left\{X_t\right\}}_{t=1,\cdots ,n}$ ，得到最初估计的变点。

定义t点的扫描窗口为

$W_t\left(h\right)=\left\{t-h+1,\cdots ,t+h\right\},$

和相应的观察值为

$X_{W_t\left(h\right)}=\left(X_{t-h+1},\cdots ,X_{t+h}\right),$

其中 $t=h,\cdots ,n-h$ ，h为窗口半径，关于h的选择详细可见第3节。

为了获得扫描窗口中初始估计的变点，可以选择似然比统计量。对于一个来自泊松INGARCH模型的样本 $d=\left(d_1,\cdots ,d_n\right)$ 的条件似然函数为

$\begin{array}{c}l\left(\theta \right)=\ln {\displaystyle \underset{t=1}{\overset{n}{\sum }}\left[p\left(d_t|d_{t-1},\cdots ,d_{t-p}\right)\right]}\end{array},$ (5)

其中 $p\left(d_t|d_{t-1},\cdots ,d_{t-p}\right)=\frac{{\text{e}}^{-{\lambda }_t}{\lambda }_t^{d_t}}{d_t!}$ 是先前给定观测值 $d_s$ 的条件密度函数，且当 $s\le 0$ 时 $d_s=0$ 。

定义扫描窗口 $W_t\left(h\right)$ 的似然比扫描统计量为

$S_h\left(t\right)=\frac{1}{h}{l}_{1h}\left(t,{\hat{\theta }}_1\right)+\frac{1}{h}{l}_{2h}\left(t,{\hat{\theta }}_2\right)-\frac{1}{h}{l}_{\cdot h}\left(t,\hat{\theta }\right),$ (6)

其中 $l_{1h}\left(t,{\hat{\theta }}_1\right)$ ， $l_{2h}\left(t,{\hat{\theta }}_2\right)$ 和 $l_{\cdot h}\left(t,\hat{\theta }\right)$ 分别是 ${\left\{X_s\right\}}_{t-h+1,\cdots ,t}$ ， ${\left\{X_s\right\}}_{t+1,\cdots ,t+h}$ 和 ${\left\{X_s\right\}}_{W_t\left(h\right)}$ 的条件似然函数， ${\hat{\theta }}_1$ ， ${\hat{\theta }}_2$ ， $\hat{\theta }$ 分别是基于序列 ${\left\{X_s\right\}}_{t-h+1,\cdots ,t}$ ， ${\left\{X_s\right\}}_{t+1,\cdots ,t+h}$ 和 ${\left\{X_s\right\}}_{W_t\left(h\right)}$ 中参数 $\theta$ 的估计量。

利用 $S_h\left(t\right)$ 扫描观测序列，可以得到一系列似然比扫描统计量 $\left(S_h\left(h\right),S_h\left(h+1\right),\cdots ,S_h\left(n-h\right)\right)$ 。假如变点为t， $S_h\left(t\right)$ 一般会较大。若选择的h，满足 $2h<n{\epsilon }_{\varpi }$ ，那么每个扫描窗口内最多存在一个变点。因此，通过局部变点位置的估计，可以得到潜在变点集合并定义为

${\hat{\mathcal{J}}}^{\left(1\right)}=\left\{m\in \left\{h,h+1,\cdots ,n-h\right\}:S_h\left(m\right)=\underset{t\in \left(m-h,m+h\right]}{\max }{S}_h\left(t\right)\right\}.$ (7)

如果 $S_h\left(m\right)$ 是以点m为中心的窗口 $\left[m-h+1,m+h\right]$ 上的最大值，则m为一个局部变点。则有一系列的初始变点 ${\hat{\mathcal{J}}}^{\left(1\right)}=\left({\hat{\tau }}_1^{\left(1\right)},{\hat{\tau }}_2^{\left(1\right)},\cdots ,{\hat{\tau }}_m^{\left(1\right)}\right)$ ，其中 ${\hat{m}}^{\left(1\right)}={\hat{\mathcal{J}}}^{\left(1\right)}$ 。

定理1记录 ${\mathcal{J}}_0=\left({\tau }_1^0,\cdots ,{\tau }_{m_0}^0\right)$ 为实际变点集，假设 $2h<n{\epsilon }_{\varpi }$ 且 ${\epsilon }_{\varpi }>c{n}^{-q}$ ，则有 $q\in \left[0,1\right)$ ， $c>0$ ，满足

$\begin{array}{c}P\left(\underset{{\tau }_i^0\in {\mathcal{J}}_0,k=1,\cdots ,{\hat{m}}^{\left(1\right)}}{maxmin}\left|{\tau }_i^0-{\hat{\tau }}_k^{\left(1\right)}\right|<h\right)\to 1\end{array}.$

定理1表明全部真实变点在初始估计变点集合 ${\hat{\mathcal{J}}}^{\left(1\right)}$ 的h-邻域内，但此时并不能保证 ${\hat{m}}^{\left(1\right)}$ 等于真实变点数量 $m_0$ 。也就是说在第一步得到的变点估计往往会有过估计问题，把一些不是变点的值当作了变点，导致 ${\hat{\mathcal{J}}}^{\left(1\right)}$ 内不但有真实变点集合，还有一些非变点。下一步将利用合适的信息准则来解决以上问题，获得一致的变点估计。定理1的证明过程可参考文献[25]。

第二步：结合MDL，得到一致变点估计。

为了从 ${\hat{\mathcal{J}}}^{\left(1\right)}$ 中找出准确的变点，可以使用MDL准则进行INGARCH模型的选择过程。定义MDL如下

$MDL\left(m,\mathcal{J}\right)=\log \left(m\right)+\left(m+1\right)\log \left(n\right)+{\displaystyle \underset{j=1}{\overset{m+1}{\sum }}2}\log \left(n_j\right)-{\displaystyle \underset{j=1}{\overset{m+1}{\sum }}{l}_j}\left({\hat{\theta }}_j\right),$ (8)

其中 $\mathcal{J}=\left({\tau }_1,\cdots ,{\tau }_m\right)$ 是第一步中得到的初始估计变点的集合 ${\hat{\mathcal{J}}}^{\left(1\right)}$ ， $\left(n_1,\cdots ,n_{m+1}\right)$ 是各段泊松INGARCH过程的长度， $l_j\left({\hat{\theta }}_j\right)$ 为第j段的似然函数类似于表达式(5)中的 $l\left(\theta \right)$ 。给定局部变点估计 ${\hat{\mathcal{J}}}^{\left(1\right)}$ ，可通过(9)进行变点估计

$\left({\hat{m}}^{\left(2\right)},{\hat{\mathcal{J}}}^{\left(2\right)}\right)=\underset{\begin{array}{c}m=\left|\mathcal{J}\right|,\mathcal{J}\subseteq {\hat{\mathcal{J}}}^{\left(1\right)}\end{array}}{\arg \min }MDL\left(m,\mathcal{J}\right),$ (9)

其中 ${\hat{\mathcal{J}}}^{\left(2\right)}=\left({\hat{\tau }}_1^{\left(2\right)},{\hat{\tau }}_2^{\left(2\right)},\cdots ,{\hat{\tau }}_{{\hat{m}}^{\left(2\right)}}^{\left(2\right)}\right)$ ， ${\hat{m}}^{\left(2\right)}=\left|{\hat{\mathcal{J}}}^{\left(2\right)}\right|$ 。

因 ${\hat{\mathcal{J}}}^{\left(1\right)}$ 里面包括的因素已很大程度上小于样本容量，故 ${\hat{\mathcal{J}}}^{\left(1\right)}$ 上使用MDL能使计算复杂度大幅度降低，很大程度的提高了计算效率。由于 $h\ge d\log \left(n\right)$ ，因此有 ${\max }_{j=1,\cdots ,m_0}\left|{\hat{\tau }}_j^{\left(2\right)}\right|=O_p\left(h\right)$ ，与 $O_p\left(1\right)$ 相比其并不理想，而MDL方法保证了 ${\tau }_j^0$ 落在区间 $\left[{\hat{\tau }}_j-h+1,{\hat{\tau }}_j+h\right]$ 的概率接近于1。那么在第三步中本文将利用这个性质定义变点的最终估计。

第三步：获得最终估计 ${\hat{\mathcal{J}}}^{\left(3\right)}$ 。

定义第j个估计变点 ${\hat{\tau }}_j^{(2)}$ 的扫描窗口 $E_j\left(h\right)$ 和相应的相应观测值 $X_{E_j\left(h\right)}$ 如下

$E_j\left(h\right)=\left\{{\hat{\tau }}_j^{\left(2\right)}-2h+1,\cdots ,{\hat{\tau }}_j^{\left(2\right)}+2h\right\},$

$X_{E_j\left(h\right)}=\left(X_{{\hat{\tau }}_j^{\left(2\right)}-2h+1},\cdots ,X_{{\hat{\tau }}_j^{\left(2\right)}+2h}\right),$

令

$l_j\left(\tau ,{\theta }_1,{\theta }_2\right)={\displaystyle {\sum }_{t={\hat{\tau }}_j^{\left(2\right)}-2h+1}^{\tau }{R}_t\left({\theta }_1\right)}+{\displaystyle {\sum }_{t=\tau +1}^{{\hat{\tau }}_j^{\left(2\right)}+2h}{R}_t}\left({\theta }_2\right),$ (10)

其中 $R_t\left({\theta }_1\right)$ 是基于序列 $\left\{X_{{\hat{\tau }}_j^{\left(2\right)}-2h+1},X_{\tau }\right\}$ 的条件似然函数，同理定义 $R_t\left({\theta }_2\right)$ ， $j=1,\cdots ,{\hat{m}}^{\left(2\right)}$ ，定义最终变点估计如下

${\hat{\tau }}_j^{\left(3\right)}=\underset{\tau \in \left({\hat{\tau }}_j^{\left(2\right)}-h,{\hat{\tau }}_j^{\left(2\right)}+h\right]}{\arg \max }{l}_j\left(\tau ,{\hat{\theta }}_j,{\hat{\theta }}_{j+1}\right),$ (11)

其中 ${\hat{\theta }}_j={\hat{\theta }}_j\left(\tau \right)=\arg \max {\theta }_1{\displaystyle {\sum }_{t={\hat{\tau }}_j^{\left(2\right)}-2h+1}^{\tau }{R}_t}\left({\theta }_1\right)$ ， ${\hat{\theta }}_{j+1}$ 定义类似。LRSM中的每一步都需要求对相应的INGARCH模型参数的估计值。将极大似然估计替换为矩估计，具体原因如下：极大似然估计法需要通过数值优化来求解，故求解过程耗费时间长；矩估计因其有显式表达式，求解过程简单，耗费时间短；虽然极大似然估计值要优于矩估计值，但通过模拟研究发现，矩估计值与极大似然估计值近似，采用矩估计值几乎不影响LRSM的性能。其参数估计详细过程见参考文献 [18] 。

2.3. 对数线性泊松INGARCH模型

尽管泊松INGARCH模型为计数相关数据的建模提供了一个适当的框架，但至少有两个与它应用相关的缺点。第一，当 $0<{\gamma }_1+{\delta }_1<1$ ，其自协方差函数大于0，故不能采用泊松INGARCH模型对负相关进行建模；第二，泊松INGARCH只包括导致正回归项的协变量，否则泊松过程的均值将有可能变为负值。为解决这一问题，Fokianos和Tjøstheim [19] 提出的对数线性泊松INGARCH模型的自相关函数可正可负。在利用LRSM进行变点探测和估计的情况下，对数线性泊松INGARCH模型与泊松INGARCH模型在步骤上相似，但是其中的一些细节需要修正。

对数线性泊松INGARCH (1, 1)模型中的式(4)是

$\{\begin{array}{l}{Y}_{t,j}|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_{t,j}\right)t\ge 1,\\ v_{t,j}={\gamma }_{j,0}+{\gamma }_{j,1}\text{log}\left(Y_{t-1,j}+1\right)+{\delta }_{j,1}{v}_{t-1,j},\end{array}$ (12)

其中参数 ${\gamma }_{j,0}$ ， ${\gamma }_{j,1}$ ， ${\delta }_{j,1}$ 属于 $ℝ$ ， $v_{t,j}\equiv \log {\lambda }_{t,j}$ ， ${\theta }_j=\left({\gamma }_{j,0},{\gamma }_{j,1},{\delta }_{j,1}\right)$ 表示第j段对数线性泊松INGARCH (1, 1)过程的参数向量。

对数线性泊松INGARCH (1, 1)模型中(5)是

$\begin{array}{c}l\left(\theta \right)=\ln {\displaystyle \underset{t=1}{\overset{n}{\sum }}\left[p\left(d_t|d_{t-1},\cdots ,d_{t-p}\right)\right]}\end{array},$ (13)

其中 $p\left(d_t|d_{t-1},\cdots ,d_{t-p}\right)=\frac{{\text{e}}^{-{\lambda }_t}{\lambda }_t^{d_t}}{d_t!}$ ，而 ${\lambda }_t=\exp \left(v_t\right)$ ，故有

$\begin{array}{c}l\left(\theta \right)={\displaystyle \underset{t=1}{\overset{n}{\sum }}\left(d_t{v}_t-\exp \left(v_t\right)\right)}\end{array}$ (14)

对数线性泊松INGARCH (1, 1)模型中(8)是

$MDL\left(m,\mathcal{J}\right)=\log \left(m\right)+\left(m+1\right)\log \left(n\right)+{\displaystyle \underset{j=1}{\overset{m+1}{\sum }}2}\log \left(n_j\right)-{\displaystyle \underset{j=1}{\overset{m+1}{\sum }}{l}_j}\left({\hat{\theta }}_j\right),$ (15)

其中 $l_j\left({\hat{\theta }}_j\right)$ 的定义类似于表达式(13)中的 $l\left(\theta \right)$ 。对数线性泊松INGARCH (1, 1)模型的参数估计类似于泊松INGARCH (1, 1)模型，其详细过程见参考文献 [19] 。

3. 窗口半径的选取

在使用LRSM的初始扫描步骤中，在给定窗口半径大小为h下，那么扫描窗口 $W_j\left(h\right)$ 的大小为2h，

$O\left(h\right)$ 是每一个时刻t的扫描统计量 $S_h\left(t\right)$ 的计算复杂度。第二步利用MDL时， $O\left({\left({\hat{m}}^{\left(1\right)}\right)}^{2}n\right)$ 是所需要的

计算复杂度。在第三步中，因在新的扫描窗口进行计算，故此时计算复杂度为 $O\left({\hat{m}}^{\left(2\right)}{h}^2\right)$ 。由以上所述，因此最终计算复杂度的总和为 $O\left(nh+h^2\right)$ 。h较小的时侯，如 $h=O\left\{log\left(n\right)\right\}$ ，那么完整的LRSM的计算复杂度为 $O\left\{nlog\left(n\right)\right\}$ ，显著低于 $O\left\{n^2\right\}$ 的数量级。

为了说明窗口半径h的选择，在本节中进行了仿真实验。LRSM中涉及的调优参数包括窗口半径h。为探讨h到底该如何取值，我们使用下面第4节中模型D随机生成的数据进行了重复试验分析，其中d分别取值(1, 2, 2.5, 3, 3.5, 4, 4.5, 5, 6, 7)，变点位置取为1250。本章将三步程序应用于长度为n = 2024的模型D重复100次进行分析研究，具有不同的h值，其中 $h=d\log {\left(n\right)}^2$ 使用不同的d值。结果汇总在表1中。

Table 1. Sensitivity analysis for the choice of h

表1. 窗口半径h的敏感性分析

$\%:{\hat{m}}^{\left(2\right)}=m_0$ 表示正确估计变点数量的百分比， $\%:\left|{\hat{\tau }}_j-{\tau }_0\right|<h$ 表示有效识别变点的百分比。

从表1的结果可以看出：较小的h被选择时虽然会减少第一步的计算成本，即 $O\left(nh\right)$ ，然而较小h的会产生非常大的 ${\hat{m}}^{\left(1\right)}$ 。也就是说，它生成了一个用于选择变点的候选池，在第二步中增加了 $O{\left({\hat{m}}^{\left(1\right)}\right)}^2$ 的计算量和计算时间。与之相反，较大的h可能带来计算上的便利但可能违反 $h<n{\epsilon }_{\varpi }/2$ 。尽管如此，从表1可以看出，对于大多数不同的h值，m的估计值是一致的，表1的结果可以说明的是当 $h=342$ 时，得到的估计结果仍很不错。这种结果的产生可能与(Vostrikova, 1981) [26] 的研究有着很大的关联，也就是当序列存在变点时，LRSM可探测出每个变点。故最终估计对h的选择并不敏感，并不会因为h取值的稍微增大或缩小影响结果。因此对于泊松INGARCH模型这里选择d = 3。

4. 模拟研究

本节进行了模拟研究，以评估应用于INGARCH模型的LRSM的性能，用统计软件R语言编程实现了仿真实验。将LRSM应用于泊松分布下的INGARCH模型和对数线性泊松下的INGARCH模型进行了探索研究，并在仿真中设置了三种场景：无变点、一个变点和两个变点。

为了简单度量LRSM的估计精度，作如下定义：一个方法若能正确的探测出变点的数量，当 $n=1024$ 或 $n=2024$ 时，以及每对真实变点与估计变点之间的距离在50内，则认为探测出来的变点是有效的。正如文献中Yau和Zhao [25] 提到的，本文也选择50。

4.1. 泊松INGARCH (1, 1)模型

在本节中，将对以下模型进行模拟研究，并对结果进行分析。模型A-F的样本路径图见图2，模拟结果见表2。

Table 2. Simulation results from Model A to Model F

表2. 模型A到模型F的模拟结果

$\%:{\hat{m}}^{\left(2\right)}=m_0$ 表示正确估计变点数量的百分比， $\%:\left|{\hat{\tau }}_j-{\tau }_0\right|<h$ 表示有效识别变点的百分比。

模型A：没有变点的平稳INGARCH (1, 1)模型

模型A场景用来测试在没有变点时的检测性能。采用多种参数组合的INGARCH (1, 1)模型： ${\lambda }_t={\gamma }_0+{\gamma }_1{X}_{t-1}+{\delta }_1{\lambda }_{t-1}$ 生成观测值，参数的选取见表2，取样本量n = 1024。从表2可以看出，LRSM是非常准确和敏感的，无错误识别变点情况。

模型B：分段平稳INGARCH (1, 1)模型(1变点)

${\lambda }_t=\{\begin{array}{ll}1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1\le t\le 512,\hfill \\ 2+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 513\le t\le 1024.\hfill \end{array}$

模型B将变点的位置设在t = 512，取样本量n = 1024，用来测试LRSM在变点靠近序列中端时的性能。从表2可以看出，LRSM正确识别变点数量的频率高达94次，且满足了估计变点与真实变点之间的距离均小于50的次数为92次。LRSM在精确的性质上表现良好。

模型C：分段平稳INGARCH (1, 1)模型(1变点)

${\lambda }_t=\{\begin{array}{ll}1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1\le t\le 512,\hfill \\ 1.5+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 513\le t\le 1024.\hfill \end{array}$

模型C将变点依然设在t = 512，且样本量相同，与模型B不同的就是参数选取的不同，用来测试LRSM在变点前后参数变化不明显时的性能。由表2可知，LRSM的性能也很好。

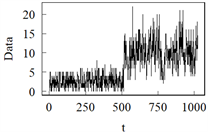
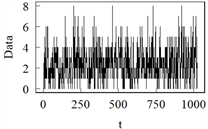
模型A 模型B

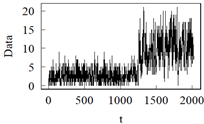
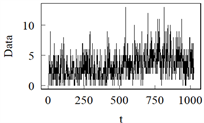模型C 模型D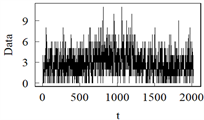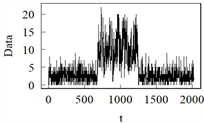模型E 模型F注：模型A中参数取1，0.2，0.4进行展示。

Figure 2. Sample path from Model A to Model F

图2. 模型A到模型F的样本路径图

模型D：分段平稳INGARCH (1, 1)模型(1变点)

${\lambda }_t=\{\begin{array}{ll}1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1\le t\le 1250,\hfill \\ 2+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1251\le t\le 2024.\hfill \end{array}$

模型D变点位置在t = 1250，样本量不同取n = 2024，用来测试随着样本量增加时LRSM的性能。由表2可知，随着样本量的增加，LRSM的性能也很好。

模型E：分段平稳INGARCH (1, 1)模型(2变点)

${\lambda }_t=\{\begin{array}{ll}1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1\le t\le 674,\hfill \\ 2+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 675\le t\le 1250,\hfill \\ 1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1251\le t\le 2024.\hfill \end{array}$

模型E分别在674和1250处设有两个变点。正确预测变点数量的频率为96，且均满足估计变点与实际变点之间的距离小于50。因此LRSM在精确的性质上表现良好。

模型F：分段平稳INGARCH (1, 1)模型(2变点)

${\lambda }_t=\{\begin{array}{ll}1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1\le t\le 674,\hfill \\ 1.5+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 675\le t\le 1250,\hfill \\ 1+0.2X_{t-1}+0.4{\lambda }_{t-1}\hfill & 1251\le t\le 2024.\hfill \end{array}$

模型F分别在674和1251处设置两个变点，与模型E参数设置不同，表现出来变点前后样本变化较小，其他相同正确预测变点数量的频率为81，满足估计变点与实际变点之间的距离小于50的次数为78，虽然比模型E稍微差点，但也能说明在变点前后变化不大时LRSM的有效性。因此LRSM在精确的性质上表现良好。

4.2. 对数线性泊松INGARCH (1, 1)模型

本节将对给出的以下几种对数线性泊松INGARH (1, 1)模型进行模拟研究，并对结果进行分析。模型G-L的样本路径图见图3，模拟结果见表3。

模型G：无变点的平稳对数线性泊松INGARCH (1, 1)模型

$X_t|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_t\right),{\lambda }_t={\text{e}}^{v_t},$

$v_t=1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}1\le t\le 1024.$

研究LRSM在对数线性泊松INGARCH (1, 1)模型的变点识别性能。加入几组不同参数组合来测试无变点时性能，不同参数组合见表3。表3可以看出，LRSM效果还是很不错的。

模型H：分段平稳对数线性泊松INGARCH (1, 1)模型(1变点)

$X_t|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_t\right),{\lambda }_t={\text{e}}^{v_t},$

$v_t=\{\begin{array}{ll}1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 1\le t\le 400,\hfill \\ 0.6+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 401\le t\le 1024.\hfill \end{array}$

模型H在400处设置一个变点，n = 1024。从表3可以看出，LRSM正确估计了变点的数量多达97次，它们都满足估计的变点与实际变点之间的距离小于50。所以LRSM在这个性质上表现的还是很不错的。

模型I：分段平稳对数线性泊松INGARCH (1, 1)模型(1变点)

$\begin{array}{c}{X}_t|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_t\right)\end{array},\begin{array}{c}{\lambda }_t\end{array}={\text{e}}^{v_t},$

$v_t=\{\begin{array}{ll}1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 1\le t\le 400,\hfill \\ 0.9+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 401\le t\le 1024.\hfill \end{array}$

模型I和模型H的样本量和变点设置相同，但参数设置不同，模型H设置的参数差距较大，模型I设置的参数差距较小。表3可以看出，当变点前后参数变化不是很明显时，LRSM也能很好地检测到变点。

模型J：分段平稳对数线性泊松INGARCH (1, 1)模型(2变点)

$\begin{array}{c}{X}_t|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_t\right)\end{array},\begin{array}{c}{\lambda }_t\end{array}={\text{e}}^{v_t},$

$v_t=\{\begin{array}{ll}1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 1\le t\le 312,\hfill \\ 0.6+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 313\le t\le 612,\hfill \\ 1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 613\le t\le 1024.\hfill \end{array}$

模型J在313和613处设置了两个变点。表3可以看出，LRSM对变点的正确估计次数高达95次，它们都满足估计的变化与实际变点之间的距离小于50。LRSM效果还是很不错的。

模型K：分段平稳对数线性泊松INGARCH (1, 1)模型(2变点)

$\begin{array}{c}{X}_t|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_t\right)\end{array},\begin{array}{c}{\lambda }_t\end{array}={\text{e}}^{v_t},$

$v_t=\{\begin{array}{ll}1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 1\le t\le 312,\hfill \\ 0.9+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 313\le t\le 612,\hfill \\ 1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 613\le t\le 1024.\hfill \end{array}$

模型J与模型K在样本量相同时设置了两个相同的变点，但是参数设置不同，模型K在参数上的差距设置很小，用来测试LRSM在变点前后参数变化较小的性能。由表3看出，LRSM效果还是很不错的。

模型L：分段平稳对数线性泊松INGARCH (1, 1)模型(2变点)

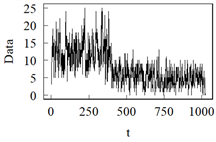
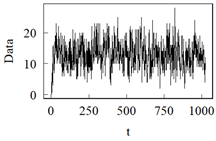
模型G 模型H

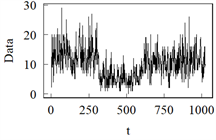
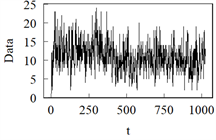模型I 模型J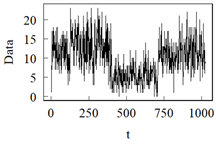模型K 模型L注：模型G中参数取1，0.4，0.2进行展示。

Figure 3. Sample path from Model G to Model L

图3. 模型G到模型L的样本路径图

Table 3. Simulation results from Model G to Model L

表3. 模型G到模型L的模拟结果

$\%:{\hat{m}}^{\left(2\right)}=m_0$ 表示正确估计变点数量的百分比， $\%:\left|{\hat{\tau }}_j-{\tau }_0\right|<h$ 表示有效识别变点的百分比。

$\begin{array}{c}{X}_t|{\mathcal{F}}_{t-1}~\mathcal{P}\left({\lambda }_t\right)\end{array},\begin{array}{c}{\lambda }_t\end{array}={\text{e}}^{v_t},$

$v_t=\{\begin{array}{ll}1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 1\le t\le 400,\hfill \\ 0.6+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 401\le t\le 712,\hfill \\ 1+0.4\log \left(X_{t-1}+1\right)+0.2v_{t-1}\hfill & 713\le t\le 1024.\hfill \end{array}$

模型L与模型J变点位置设置不同，其他均相同，用来测试变点位置设置不同时LRSM的性能。由表3看出，LRSM还是有效的。

5. 实证分析

5.1. 癫痫发作次数数据

癫痫是一种神经疾病，由于脑内的神经细胞异常放电，突然引起脑功能障碍，出现暂时性的异常行为、感觉和意识障碍、肌肉痉挛等症状。癫痫发作次数数据指的是患者在一段时间内，通常指的是每天的发作次数。癫痫发作次数数据的收集和记录对于医生和研究人员来说很重要，因为它可以用来评估患者病情的严重程度、治疗的有效性和疾病的倾向。通过分析癫痫发作次数数据，医生可以制定个性化的治疗方案，预测未来的发作风险，评估药物的有效性和研究癫痫的病理生理。在统计分析中，癫痫发作次数数据通常被视为时间序列数据，时间序列分析方法可以应用于研究发作频率的趋势、季节的变化和预测未来的发作。更为重要的是，变点检测方法也可以用来识别癫痫发作次数的变点，帮助医生调整治疗方案。

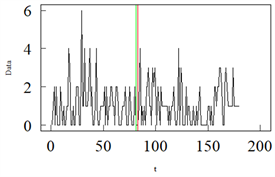
Figure 4. Epileptic seizure counts data

图4. 癫痫发作次数数据

每日癫痫发作次数是评估各种治疗方法有效性的重要信息来源，尤其是评估抗癫痫药物的使用情况。本节基于LRSM利用泊松INGARCH (1, 1)模型对癫痫发作次数数据进行变点探测。该数据来自于Franke和Kirch [27] ，其样本长度为180，样本路径图如图4所示。这些数据是一项大型临床研究的一部分，该研究调查了一种药物对部分癫痫发作的影响。首先癫痫发作次数记录在常规药物下的一段时间，然后从 $t=80$ 时患者接受安慰剂。Franke和Kirch [27] 对该数据利用泊松INGARCH (1, 1)模型进行拟合并运用累计和方法探测到变点位置在 $t=81$ 。本节运用LRSM探测到变点位置在 $t^{*}=83$ 。为此，对这两个可能的变点分别进行泊松INGARCH (1, 1)模型拟合，并计算了均方误差。当计算得到变点为第81天时，通过拟合的泊松INGARCH (1, 1)模型得到预测值的均方误差为2.284；变点为第83天时，其

均方误差为2.045，其均方误差的计算公式为 $MSE=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\hat{y}}_i\right)}^2}$ ，其中n为样本量， $y_i$ 为实际观测值，

${\hat{y}}_i$ 为预测值。这明显地表明，使用变点为第83天时的泊松INGARCH模型更适合该组数据。参数估计如下表4。

Table 4. Parameter estimation of the Poisson INGARCH (1, 1) model

表4. 泊松INGARCH (1, 1)模型参数估计

5.2. 弯曲杆菌数据

查阅相关资料得到，弯曲杆菌病是由弯曲杆菌属细菌感染引起的急性细菌感染。主要攻击人体的消化系统，然后引发疾病，是导致胃肠炎最为常见的细菌。其中大多数患者在感染2到5天后就出现症状的现象比较常见，但是也有可能连续1天到1周，更有可能10天。弯曲杆菌感染一般来说是比较轻微的，其中腹泻、腹痛、发烧、恶心或呕吐等现象是最为常见的临床症状，一般持续3到6天。但是，弯曲杆菌可能进入血液循环。因此，对于非常年幼的儿童、老年人、免疫缺陷的人来说是致命的。

Figure 5. Campylobacter data

图5. 弯曲杆菌数据

Table 5. Parameter estimation of the Log-linear Poisson INGARCH (1, 1) model

表5. 对数线性泊松INGARCH (1, 1)模型参数估计

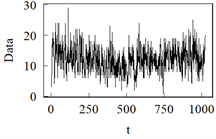
本节基于LRSM运用对数线性泊松INGARCH模型对弯曲杆菌数据 [19] 进行变点探测。这组数据记录了1990年2月至2000年10月期间加拿大魁北克省北部弯曲杆菌感染患者的数量。该地区每28天记录一次弯曲杆菌感染病例，每年进行13次观察。选取前120个数据，绘制时间序列图，如图5所示。由图5可以看出，在t = 70之前，魁北克省北部弯曲菌病感染人数保持相对稳定的波动，但在t = 70之后，弯曲菌病感染人数“激增”并迅速达到最大值。对数线性泊松INGARCH (1, 1)模型与该数据进行了拟合，并使用LRSM检测变点，在t = 73处检测到变点。这里使用赤池信息准则(AIC)和贝叶斯信息准则(BIC)在无变点模型和有变点模型中选择一个最优模型。当变点为73时的AIC值和BIC值分别为702和717，当无变点时的AIC值和BIC值分别为763和774。最小信息量表明，无论采用AIC准则还是BIC准则，有变点的对数线性泊松INGARCH (1, 1)是相对较优的模型。当变点为73时的均方误差为2.282；无变点时的均方误差为4.664，这也表明了，变点为第73天的对数线性泊松INGARCH (1, 1)模型拟合效果更好。其参数估计如上表5。以上说明了LRSM的有效性。

6. 结论与展望

本文主要研究了分段平稳的INGARCH模型变点探测问题，运用LRSM对变点数目及位置进行探测和估计。最后，将LRSM应用于两个真实的数据集中。通过模拟研究和真实数据分析的结果表明：LRSM能有效的探测出由INGARCH模型生成的分段平稳整数值自回归过程中的变点。

基金项目

辽宁科技大学博士启动基金(601010391)。

NOTES

^*通讯作者。