竖向振动加速度三维特征图在地基注浆加固质量检验中的应用

Application of Three-Dimensional Characteristic Diagram of Vertical Vibration Acceleration in Quality Inspection of Foundation Grouting Reinforcement

摘要: 动力设备基础注浆加固效果的质量检验通常采用标准贯入、静力触探等原位测试方法，但是生产繁忙、空间狭小的厂房无法满足原位测试条件。由此，本文提出了一种地基注浆加固质量检验的振动加速度三维特征图法：在加固范围内合理选取测点，采集各测点的三维加速度时程记录；分析反映能量特性(均方值、方差、均方根值)、冲击特性(峰值因数、脉冲因数、裕度因数)、分布特性(峭度、偏度指标、偏态因数)的时域指标，在三维坐标系中绘出各指标的特征点，加固前、后所有测点的特征点形成振动加速度三维特征图，由此可以直观、全面、准确地评价地基加固效果。通过研究一大型精密设备地基注浆加固工程验证了该方法的有效性：加固后各测点反映能量、冲击、分布特性的时域指标均有不同程度的降低，表明注浆加固效果良好。

Abstract: The quality inspection of grouting reinforcement effect of power equipment foundation usually adopts in-situ test methods such as standard penetration and static cone penetration. However, the factory with busy production and narrow space cannot meet the in-situ test conditions. Therefore, in this paper, a three-dimensional characteristic diagram method of vibration acceleration for quality inspection of foundation grouting reinforcement is proposed: The testing points are reasonably selected in the reinforcement range, and the three-dimensional acceleration time-history records of each testing point are collected. The time domain indexes reflecting energy characteristics (mean square value, variance, root mean square value), impact characteristics (crest factor, pulse factor, margin factor), and distribution characteristics (kurtosis, skewness index, skewness factor) are analyzed. The characteristic points of each index are drawn in the three-dimensional coordinate system. The characteristic points of all testing points before and after reinforcement form a three- dimensional characteristic diagram of vibration acceleration. Therefore, the effect of foundation reinforcement can be evaluated intuitively, comprehensively, and accurately. The effectiveness of the method is verified by studying a foundation grouting reinforcement project of large precision equipment: After reinforcement, the time domain indexes reflecting the energy, impact, and distribution characteristics of each testing point after reinforcement are reduced to varying degrees, indicating that the grouting reinforcement is effective.

1. 引言

当地基的变形性能和承载力不能满足工程设备的要求时，就要对地基进行加固处理，以提高其承载力并改善其变形性能。注浆技术在实际运用中存在施工简单易行、绿色环保、影响范围小 [1] 等优势，在地基处理当中被广泛应用，而注浆加固后地基的质量检验也是必不可少的。

依据《建筑地基处理技术规范》(JGJ 79-2012)中对注浆加固工程质量检验的要求，可选用标准贯入试验、静力触探试验或轻便触探试验对加固地层进行检测，并且对注浆效果的评定应注重前后数据的比较，以综合评价注浆效果 [2] 。对于注浆加固后的地基，也应依据《复合地基技术规范》(GB/T 50783-2012)的规定，根据检测目的和工程特点选择合适的检测方法 [3] 。且原位测试是在岩土体原有位置上测试工程性质的检验手段，要根据《建筑地基检测技术规范》(JGJ 340-2015)中各原位测试的场地条件及试验器具的要求，合理地进行质量检验 [4] 。综合厂房及机器设备的场地条件，发现场地操作环境不符合仪器设备的使用要求。那么，当出现工程场地无法满足原位测试现场条件的情况时，如何进行加固效果的评价以及质量检验是我们主要研究解决的问题。

振动速度、加速度以及峰值、均方根值、频率等时域、频域指标在地基动力响应、振动衰减规律、加固效果评价等方面的应用广泛。在地基动力响应方面，马文杰等 [5] 通过研究桩基的速度时程曲线及其峰值变化，探究了层状非饱和土中桩基的竖向振动响应。Sharma等 [6] 在六个不同的动态力水平下，从位移–频率变化的角度研究了未加固和加固条件下的地基动力响应，以评价地基基础性能改善与否。陈志雄等 [7] 通过分析地基土的加速度、沉降位移等，对桩顶承台竖向荷载作用下不同桩群的振动响应进行了对比研究。在地基振动衰减方面，许照刚等 [8] 通过测量对比注浆与非注浆区域的地面振动速度等振动响应，研究了水泥注浆改性卵石土对地面振动的衰减作用。王沁平等 [9] 通过振动测试反映了某软土地基的振动衰减规律，并评估了其振动水平。陈进 [10] 通过研究软夹层地基上桩–土–层间隔震结构的动力响应和减震性能，探究了不同地基土性和夹层厚度对减震效果的影响并提出了建议。在地基加固效果评价方面，Qu等 [11] 通过分析球磨机的振动冲击对基础瞬态响应的影响，来研究机器基础加固后的整体稳定性。郭乾等 [12] 根据加固前后振动加速度变化，分析了黏土夹层对土体强度、能量传递规律的影响，进而研究了其对地基加固效果的影响。程远等 [13] 通过振动试验，研究了不同工况和不同频率下的地表振动响应以及振动能量的传递和衰减规律，并将原位测试方法与振动响应相结合来评价地基加固效果。

根据各位学者的研究，发现对于地基振动的研究主要从时域、频域等方面开展，并将振动法与各种原位测试相结合来评价地基加固效果；但是已有工作大多采用振动峰值、均方根值、固有频率等单一时域、频域指标，这些指标难以综合评价地基的加固效果。由此，根据各时域指标的物理意义不同，本文提出采用振动加速度三维特征图的方法，更加全面、直观、准确地来评价地基的注浆加固效果。

为解决无法通过原位测试进行地基质量检验的问题，本文从振动测试的角度提出了振动加速度三维特征图来评价地基的注浆加固效果。首先，测量选定测点的振动加速度，获得各测点的加速度时程曲线；其次，在时程曲线中提取出各时域指标；最后，绘制振动加速度三维特征图并进行分析。振动测试法具有方便快捷、时间跨度小、占地范围小，且具备更广泛的适用性和安全性等特点。并且测试仪器方便携带，可布置在建筑结构外部，不会对基础或任何结构造成损坏(即无损检测)。结合加固前后的实测数据，发现竖直方向的时域指标与水平方向相比变化较大且较为规律，由此本文主要研究地基的竖向振动加速度信号，并进行其时域指标的三维特征分析。

2. 振动加速度三维特征图

振动量一般有振动位移、振动速度以及振动加速度等，通常采用峰值、均方根值或其它参数来描述振动量。由于振动加速度反映了冲击力的大小 [9] ，因此振动加速度是表征结构物振动的重要振动量。实际工程中测量所得的振动信号一般都是随机的离散信号，通常采用具有统计特性的信号参数来进行信号分析 [14] ，这些参数包括均方根、均值、方差、偏度、峭度和裕度等 [15] 。

根据各时域指标表征的物理意义不同，分析得到反映能量特性、冲击特性、分布特性的时域指标；在能量、冲击、分布的三维坐标系中画出该测点的各指标数据无量纲化后的特征点(X_k, Y_k, Z_k)，加固前后所有测点的特征点在能量(同冲击、分布)坐标系中的位置表现形成了能量特性(同冲击、分布)三维特征图。表征能量、冲击、分布特性的时域指标三维特征图组成了振动加速度三维特征图。振动加速度三维特征图法的分析流程如图1所示。

无量纲化定义为：以加固前的数据作为参照标准，加固后与加固前的数据全部去除以该值，实现数据的无量纲化。由于加固前的数据除以其本身得到数字1，那么可以得到加固前的特征点为(1, 1, 1)；则主要考虑加固后数据的无量纲化计算，公式为：

$X_k=\frac{x_{kb}}{x_{ka}}{Y}_k=\frac{y_{kb}}{y_{ka}}{Z}_k=\frac{z_{kb}}{z_{ka}}$ (1)

式中， $k=1,2,3,\cdots ,n$ ，n为测点数；下标a表示加固前的指标，b表示加固后的指标。

Figure 1. Flow chart of method analysis in this paper

图1. 本文方法分析流程图

2.1. 能量特性指标

通过对采样信号进行带通滤波，然后计算出滤波后数据的均方值或均方根值，这样便得到相对应的功率谱值或幅值谱值 [16] 。由于功率谱密度由几次测量信号的傅里叶变换后幅值平方的均值得到，幅值的平方与信号的能量有关，故均方根值反映了动态信号的能量强度，且具有较好的稳定性 [17] ；方差反映了信号绕均值的波动程度，是描写数据的动态分量与随机振动的能量成比例 [16] 。均方值、均方根值、方差减小，则功率谱值或幅值谱值减小，表明设备传递的能量得到耗散。

综上，均方值(E)用来描述信号的平均能量或平均功率，又称二阶矩 [16] 。其公式定义为：

$E=\frac{1}{T}{\displaystyle {\int }_0^T{x}^2\left(t\right)}dt$ (2)

方差(D)代表了信号能量的动态分量，反映了信号绕均值的波动程度，具有较好的敏感性，因而可以代表数据段的振动强度平均水平 [18] 。其公式定义为：

$D=\frac{1}{T}{{\displaystyle {\int }_0^T\left[x\left(t\right)-\bar{X}\right]}}^{2}dt$ (3)

信号的均方根(RMS)即有效值是信号平均能量的一种表达 [16] [18] ，它反映了振动信号的能量强弱。其公式定义为：

$RMS=\sqrt{\frac{1}{T}{\displaystyle {\int }_0^T{x}^2\left(t\right)}dt}$ (4)

式中，x(t)为振动加速度信号，T为采样点数，其中 $\bar{X}$ 为平均值，公式为：

$\bar{X}=\frac{1}{T}{\displaystyle {\int }_0^{T}x\left(t\right)}dt$ (5)

均方值、方差、均方根值都是表征信号能量波动变化的指标，可将三者组成特征点(E, D, RMS)用于分析加固前后振动信号的能量特性变化。若均方值、方差、均方根值均减小，则说明信号绕均值的波动程度减小、振动信号的能量变弱，即设备产生的能量得到有效耗散，其振动特性变好，反之亦然。

以能量特性指标变化为例，首先对加固前后的均方值、方差、均方根值进行无量纲化，可得到加固前的特征点为(1, 1, 1)，加固后的特征点数值由公式(1)进行计算。将各特征点在三维坐标系中绘出，若加固后的各三维特征点位于加固前特征点的下侧，且在两两对应的坐标系中，加固后各点的位置均位于加固前的左下侧，如图2中A点所示，则说明加固后的各时域指标较加固前变小，地基的振动特性变好。若加固后的各三维特征点位于加固前特征点的上侧(两两对应的坐标系中为右上侧)，如图2中B点所示，则说明加固后的各指标较加固前变大，地基的振动特性变差，注浆加固效果不理想。

Figure 2. Three-dimensional characteristic diagram example of energy characteristic index change

图2. 能量特性指标变化情况的三维特征图示例

本文案例中若出现各时域指标减小的变化，则说明振动特性变好，注浆加固效果良好。冲击特性与分布特性的指标变化分析方法同上。

2.2. 冲击特性指标

峰值因数(CR)是信号峰值与均方根值的比值，代表的是峰值在波形中的极端程度 [19] 。其公式定义为：

$CR=\frac{\max \left|x\left(t\right)\right|}{X_{RMS}}$ (6)

脉冲因数(IM)是信号峰值与整流平均值的比值。其公式定义为：

$IM=\frac{\max \left|x\left(t\right)\right|}{\frac{1}{T}{\displaystyle {\int }_0^T\left|x\left(t\right)\right|}dt}$ (7)

裕度因数(CL)是信号峰值与方根幅值的比值。其公式定义为：

$CL=\frac{\max \left|x\left(t\right)\right|}{{\left(\frac{1}{T}{\displaystyle {\int }_0^T\sqrt{\left|x\left(t\right)\right|}}dt\right)}^2}$ (8)

其中，x(t)为振动加速度信号，T为采样点数， $\bar{X}$ 为平均值，见公式(5)。

峰值和峰值因数可以用作为设备振动的强度和烈度等指标，也可以很好地确定信号的冲击与不稳定性 [20] 。峰值、裕度和脉冲等指标对脉冲信号的瞬态冲击特性较为敏感，且随着故障程度的增加而增加 [17] 。随着峰值因数的增大，信号包括的冲击振动也越来越明显；随着裕度因数的增大，信噪比增大，分段信号的冲击效果越明显 [20] 。所以，峰值因数、裕度因数、脉冲因数减小，使得信号的冲击效果减弱。

由此，可将脉冲因数、峰值因数、裕度因数组成特征点(IM, CR, CL)用于分析加固前后振动信号的冲击特性变化。若这三个指标减小，则说明振动信号中存在的冲击成分减少，即所受到的振动冲击效果减弱，表明振动特性变好，反之亦然。

2.3. 分布特性指标

峭度(K)是用以表示波形平缓程度的，用于描述变量的分布，峭度小于3时分布的曲线会较“平缓”，大于3时分布的曲线较“陡峭” [21] 。当峭度K = 3时，信号的幅值分布接近标准正态分布；K值越大，则表示信号中较大幅值数据的概率密度增加 [22] 。其公式定义为：

$K=\frac{1}{T}{{\displaystyle {\int }_0^T\left[x\left(t\right)-\bar{X}\right]}}^{4}dt$ (9)

峭度为信号的第四个标准化矩；与峭度相似，偏度是第三个标准化矩，它是对随机变量的概率分布不对称性的一种度量，用来定量描述其偏离正态分布的情况 [23] 。偏度指标(SK)反映振动信号的非对称性，除有急回特性的机械设备外，由于存在着某一方向的摩擦或碰撞，造成振动波形的不对称性，使其值增大 [20] 。其公式定义为：

$SK=\frac{1}{T}{{\displaystyle {\int }_0^T\left[x\left(t\right)-\bar{X}\right]}}^{3}dt$ (10)

偏态因数(Cs)是通过比较众数或者中位数与均值来衡量偏斜度，其反映随机信号的幅值概率密度函数对于纵坐标的不对称性，不对称越厉害，斜度越大 [24] 。其公式定义为：

$Cs=\frac{\frac{1}{T}{{\displaystyle {\int }_0^T\left[x\left(t\right)-\bar{X}\right]}}^{3}dt}{{\left(\sqrt{\frac{1}{T}{{\displaystyle {\int }_0^T\left[x\left(t\right)-\bar{X}\right]}}^{2}dt}\right)}^3}$ (11)

其中，x(t)为振动加速度信号，T为采样点数， $\bar{X}$ 为平均值，见公式(5)。

当SK = 0 (Cs = 0)时，振动信号关于x轴对称；当SK > 0 (Cs > 0)时，振动信号为右偏(正偏态)；当SK < 0 (Cs < 0)时，振动信号为左偏(负偏态)。由此，可将峭度、偏度指标、偏态因数组成特征点(K, SK, Cs)用于分析加固前后振动信号的分布特性变化。偏度指标、偏态因数、峭度的减小，使得振动波形的不对称性减弱，偏斜程度减弱，信号中较大幅值数据的概率密度减小，分布的曲线会较“平缓”，表明振动特性变好，反之亦然。

3. 工程概况与振动测试方案

3.1. 工程概况

以某精密设备地基注浆加固工程为研究对象，该设备主要用于钢铁的精细切削加工以及轮廓的外形加工，重复定位精度误差为±3 μm。建设之初，该设备的基础直接建在夯土地基上并未采用桩基础，而机器正常运行时产生的不平衡扰力使其产生振动，其中有很大一部分能量传到地基中，以致引起地基运动，导致其发生形变、造成不均匀沉降。又因夯土的工程性质不均、雨期地下水位上升等原因，地基承载力、变形模量、抗剪强度等物理力学指标均有下降，地基的不均匀沉降更加明显，使得加工构件时同一直线圆孔的削切产生错位，不能保证产品的加工精度要求。所以需要对该设备的地基进行注浆加固处理，以解决地基不均匀沉降导致的加工精度的降低。

3.2. 振动测试方案

3.2.1. 测试仪器

每一种传感器有其各自可适用的情况，在测试时，应根据测试结构及测试内容选择最恰当的传感器。基于不同目标的传感器选择因素有很多，总结如下：灵活性、能控性、效率与鲁棒稳定性能等 [25] 。振动加速度反映了冲击力的大小，且一般加速度传感器的测量带宽比较大，可以获得比较丰富的高频成分 [26] ，本试验选择加速度型传感器对振动加速度信号进行采集，试验采样频率设置为1024 Hz。

Figure 3. Data acquisition equipment

图3. 数据采集设备

941B型拾振器、COINV数据采集仪以及用于示波显示、数据存储的笔记本电脑 [19] 相连接组成一套完整的振动信号的采集设备，如图3所示。

3.2.2. 测点布设

传感器的布点主要针对加固区域范围之内；且加固的最终目的是为保证产品的加工精度要求，所以只考虑对机器运行状态下的地基振动信号的采集。基于以上，在该设备基础及其周边共设置了8个测点，每个测点都布设竖直、东西与南北三个方向的传感器。其中，测点2、4、6、8位于机器基础上，其余测点均位于地面工作台上，各测点分布位置如图4所示。

Figure 4. Distribution map of testing point position

图4. 测点位置分布图

传感器布置的原则是保证测试前后传感器的布点位置及布置方向和传感器的编号相对应。这样做的好处是便于后续的数据处理，不至于引起数据混乱和数据不对应的问题。同时，也保证了加固前后两次比对数据的可靠性，避免因不同传感器的灵敏度、线性度、瞬态响应等的差异而产生测试误差。同样地，传感器节点之间的时间同步对于基于振动的准确识别至关重要 [27] 。振动法产生的波动是振动的传播，在激发荷载作用下的振动不会立刻影响其他部位，其传播需要时间，并经过一定的通道 [28] 。所以，加固前后振动采集的时长均不低于300 s。

4. 时域指标三维特征图对比分析

通过对加固前后各测点进行振动测试，采集振动加速度信号，绘制出加固前后的振动加速度时程曲线对比，并在时程曲线中提取出各时域指标进行分析。

Figure 5. Comparison of acceleration time-history curves of testing points 1 (a) and 2 (b)

图5. 测点1 (a)、2 (b)加速度时程曲线对比

以测点1、2为例，绘出加固前后4 s内的振动加速度时程曲线对比，如图5所示。地基加固前后，各测点时域指标的变化对比如表1所示。按照式(1)，将表1中各测点能量特性、冲击特性、分布特性指标的实测数据进行无量纲化计算，并绘制出各时域指标的三维特征图进行分析，如图6、图7所示。

Table 1. Comparison of time domain indexes of each testing point before and after foundation reinforcement

表1. 地基加固前后各测点时域指标对比

从图中可以发现，加固后的各三维特征点均位于加固前特征点的下侧；且在两两对应的坐标系中，加固后各点的位置均位于加固前的左下侧，说明注浆加固后振动信号的各时域指标均减小。

由图6、图7的特征分析可以得出：

1) 反映振动信号能量特性的均方值、方差与均方根值均减小，表明加固后设备运转产生的能量有效耗散，造成的振动信号的波动程度减小，以及加固后地基整体的振动强度降低，说明加固后地基的振动特性变好。

2) 脉冲因数、峰值因数与裕度因数反映信号的冲击特性，加固后各因数减小，表明振动信号中存在的冲击或信号突变成分减小，加固后地基所受到的振动冲击效果减弱，说明加固后地基的振动特性变好。

3) 峭度、偏度指标与偏态因数是信号的分布特性的反映，由表1数据可知，部分测点的偏度指标、偏态因数小于零，为负偏态(即左偏斜分布)；将偏度指标与偏态因数取绝对值后与峭度进行分析，三者均减小，表明地基振动信号的整体分布逐渐变得平缓，偏离正态分布的不对称性减弱，偏斜程度降低，说明地基的振动特性变好。

Figure 6. Three-dimensional characteristics diagrams of time domain indexes of energy characteristics (a), impact characteristics (b), and distribution characteristics (c) of testing points 1~4

图6. 测点1~4的能量特性(a)、冲击特性(b)、分布特性(c)的时域指标三维特征图

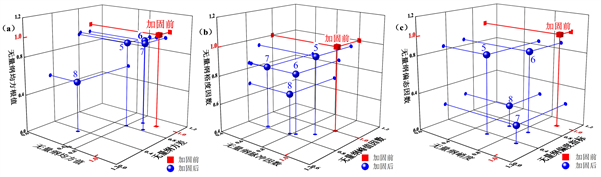
Figure 7. Three-dimensional characteristics diagrams of time domain indexes of energy characteristics (a), impact characteristics (b), and distribution characteristics (c) of testing points 5~8

图7. 测点5~8的能量特性(a)、冲击特性(b)、分布特性(c)的时域指标三维特征图

5. 结论

本文基于振动测试提出采用振动加速度三维特征图进行地基注浆加固质量的检验，即：分析反映能量特性、冲击特性、分布特性的时域指标，在三维坐标系中绘出各指标的特征点，通过分析加固前后的特征变化，可以直观、全面、准确地评价地基加固效果。

并得出以下结论：通过对反映能量特性、冲击特性、分布特性的时域指标三维特征图的分析，发现各时域指标均有不同程度的减小，说明加固后振动信号的整体分布较为平缓、偏斜程度降低，并且加固后设备运转产生的能量有效耗散，地基所受到的振动冲击程度减弱，即地基的整体振动特性变好，注浆加固效果良好。

且基于振动测试的振动加速度三维特征图分析可以与多种原位检测手段相结合，综合分析后确定地基的加固效果，为地基的安全性提供可靠的保障。

基金项目

山东省研究生质量工程提升项目(SDYYZKC2021168)。