1. 引言
为了解释光学系统中某些处于平衡状态的不寻常现象,例如方向依赖性、非局域非线性效应和光学相位变换点,Bender和Boettcher [1] 在1998年提出了PT对称势非线性薛定谔方程(Nonlinear Schrödinger Equation, NLSE)的两类反问题对称性的概念。将PT对称势NLSE的两类反问题对称势引入非线性薛定谔方程,可以描述光子在介质中传播时由于光的非线性效应而产生的光孤子的演化现象。光孤子是一种特殊的光波现象,具有保持形状和能量的稳定性,在光电信息处理、光存储、光计算等领域具有重要的应用。通过控制和操纵光孤子的产生、传播和相互作用,可以实现信息传输、信号处理和光学计算等功能,这在现代光学中具有重要意义 [2] [3] [4] [5] [6] 。
从20世纪80年代开始,学者们开展了非线性薛定谔方程(NLSE)的反问题研究,旨在通过已知的输入波场来推断NLSE中的非线性系数和势函数。这项研究为新型光学器件的设计提供了理论基础。在NLSE中,色散系数和非线性项系数的反演可以揭示光子的非线性传输过程,而势函数的反演可以提供量子系统实际的势阱形状信息,影响整个量子系统的性质和动力学行为。目前,对NLSE的反问题研究主要集中在数值理论和方程参数优化两个方面。在数值理论方面,Hogan等 [7] 通过分析NLSE的小幅度波束解,采用变分法确定解的非线性相位,从而实现了对三次非线性项参数的反演。Murphy [8] 提出了一种基于散射变分原理的方法来研究NLSE中衍射色散系数的反演问题,为理解NLSE的散射映射与未知系数之间的关系提供了新思路。在方程参数优化方面,S. A. Avdonin等 [9] 通过NLSE的波动系数演化数据,构建了最小二乘优化问题,以恢复NLSE中的势函数V(x)。Baudouin L.等 [10] 通过分析求解方法,推导出变分公式,并在严格的理论证明中表明其在特定条件下具有唯一的稳定解,并用于研究NLSE中势函数的确定问题。然而,上述关于NLSE反问题的研究都是从理论分析的角度展开的,并没有给出对应这一反问题的数值求解算法。因此,开发更有效的数值求解算法对于光学领域中的NLSE反问题至关重要。
近年来,新兴的神经网络方法为NLSE的正问题和反问题求解提供了新的途径 [11] 。例如,Raiss等 [12] 提出了基于神经网络的物理约束神经网络方法(Physics-Informed Neural Networks, PINNs)。PINNs的核心思想是利用神经网络来逼近NLSE的解,并将物理方程作为附加的约束条件,从而在单一训练过程中同时求解方程和估计参数。这种方法的优点在于避免了传统数值方法中的重复求解方程的步骤,从而提高计算效率。另外,Zhou等 [13] 使用深度神经网络解决了非线性薛定谔方程及其逆问题,来确定PT对称调谐势下的系统参数。Song等 [14] 则利用PINNs将PT势函数的先验信息引入损失函数中,以获得同时满足先验和给定数据信息的势函数。然而,如果没有势函数的先验信息,目前尚不清楚这种方法是否仍然有效,还需要进一步验证。需要指出的是,尽管已有研究对具有PT对称势的反问题进行了探索,但现有的数值求解方法的普适性仍然不够强,计算效率也相对较低,这两个方面仍有改进的空间。特别是对于复杂的PT势函数反演问题,在没有先验信息的情况下求解依然存在困难。
在具有PT对称势的NLSE方程中,涉及色散系数、衍射系数以及相应的势函数。其中,色散系数是影响光纤通信质量的一个主要因素,光纤色散会导致脉冲展宽,造成光信号畸变,影响传输距离的长短。衍射系数则是刻画非线性光学效应中介质的非线性偏振率,它决定了光波在传播时对自身产生的影响效应,使光波的包络发生聚焦或散焦。因此,研究色散系数和衍射系数平衡规律,以及具有良好性质的PT对称势,有助于理解光孤子在非线性光学系统中的稳定性。
本文则对带有PT对称势的NLSE提出了两类反问题。其中,第一类问题是色散系数和衍射系数的反演问题:通过已知的输入数据和势函数来推断,推断NLSE中的色散系数和非线性系数。第二类问题则是PT对称势函数的反演问题:通过部分测量数据和给定色散系数和衍射系数,恢复NLSE中的势函数,即量子系统中的势阱形状信息。这两类反问题的研究对于我们更好地理解带有PT对称势的NLSE中的非线性现象和光传播系统的性质具有重要意义。同时,它们也为光学器件设计和量子光学领域的进展提供了理论基础。进一步,在第一种有关反射系数和衍射系数的反问题的求解中,我们应用PINNs深度学习方法和经典粒子群算法(PSO)结合有限差分数值求解的方法分别进行求解,以期比较这两种算法对于这类反问题求解的计算效率。而对于第二种有关势函数的反问题中,我们提出一种带有自适应基函数的PINNs算法,以期通过在自适应基函数中引入sigmod和tanh函数来提高PINNs算法的计算精度。值得注意的是这种带有自适应基函数的PINNs算法不需要指定势函数的形式,也不需要提供先验信息,即可求解满足给定条件的势函数。
本文结构如下。在第2节中对带有PT对称势的三次和五次幂律NLSE分别提出两类反问题。第3节我们给出了两类反问题对应的损失函数,提出利用物理信息神经网络(PINNs)深度学习方法来求解所提出的两类反问题。第4节中给出数值实验。第5节中我们对本文的主要工作和贡献进行总结。
2. PT对称势NLSE的两类反问题
在本章中,我们先通过具有PT对称势NLSE正问题来构建两类反问题。
2.1. 具有PT对称势的NLSE正问题
我们首先给出一维带有PT对称势的三次和五次幂律非线性薛定谔方程的正问题,即考虑如下形式的非线性薛定谔方程 [15] :
 (1)
(1)
其中,
是具有缓慢变化电场包络的复值函数,代表光的传播,其中x代表横向坐标,z表示无量纲纵向传播距离。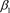 表示横向坐标的色散系数,
和
分别代表三次和五次的非线性项,也称作衍射系数。
表示具有PT对称势函数。
表示横向坐标的色散系数,
和
分别代表三次和五次的非线性项,也称作衍射系数。
表示具有PT对称势函数。
我们将(1)的解定义在整个域
上,其中
。我们将初始域 分为三个区域,用
表示需要计算近似解的内部域,另外两个互补区域分别为:
和
。该NLSE方程(1)的初始边界条件为:
分为三个区域,用
表示需要计算近似解的内部域,另外两个互补区域分别为:
和
。该NLSE方程(1)的初始边界条件为:
(2)
其中,
和
是光滑函数。
表示
的边界。
根据NLSE方程(1)~(2),如果我们已经确定了方程的参数
、
、
和具有PT对称性的势函数
,那么我们就可以确定光束的传播状态。在这种情况下,我们需要思考的问题是,如果我们观察到部分光束的状态并且已知对称势函数
,那么相应的色散系数
以及衍射系数
和
会是什么样的?另外,我们还需要弄清楚如何确定这些非线性系数。进一步地,如果我们观察到部分光束的状态并且已知非线性系数
和
、
,那么满足PT对称性的势函数
会有怎样的特征?该如何找到适合这个光束状态的势函数呢?接下来,我们将逐步解决这些问题。
2.2. 关于色散系数和非线性系数的反演问题
在符合具有PT对称性NLSE方程的光束传播中,如果色散系数远大于衍射系数,则色散效应起主导作用。过强的色散效应将导致光波包络衰减过快,难以长距离传播;而如果衍射系数远大于色散系数,则衍射效应起主导作用,在包络方程的演化过程中,会出现急剧的自聚焦现象,导致波函数在短距离内崩溃。而当二者的量级接近时,非线性色散效应将发挥作用。因此确定适当的色散和衍射系数对于保证通信质量至关重要。那么我们目前希望解决的是根据观测到的一部分光束数据,在已知对称势函数的情况下,确定色散系数和衍射系数,即色散系数和衍射系数的反演问题。
为了建立色散–衍射反问题,我们首先对正问题的传播进行分析。当色散系数、衍射系数以及对称势函数确定时,根据NLSE方程(1)~(2)确定的光束传播状态也将确定,并能够获得每个点处光束的确切数据。换种说法就是,如果我们已经测量到了部分光束的数据,那么对应的NLSE方程中的参数必定是预先给定的数据。然而,如果只有势函数相同而色散系数和衍射系数发生改变,那么产生的光束数据也会相应发生变化。因此,在势函数相同的情况下,我们可以根据测量到的部分光束数据来估计产生这些数据的参数,这可以通过比较测量数据和变换参数所导致的光束计算数据之间的差异来建立一个优化问题。这个优化问题的目标是将这两者的差异最小化,从而找到能够在NLSE方程中产生测量到的光束数据的相关参数。
假设
,其中表示N个测量点,
表示在这些测量点上得到的测量数据,而
则是在NLSE方程(1)~(2)的不同参数
计算得到的数据。我们的目标是在
范数的意义下最小化这两者之间的差异。
可以将优化问题表述如下:
(3)
其中,
表示计算数据和测量数据在点
处差异。通过对所有测量点处二者差异的和进行优化,我们希望找到一组最优的参数
,使得计算数据
和测量数据
的差异最小化。
2.3. 关于势函数反演问题
带有PT对称势的NLSE方程中的对称势函数在研究和应用上具有多重重要作用。首先,对称势函数确保系统解的实数性,保证波函数和能量等物理量是实数,从而维持系统的稳定性和可行性。其次,对称势函数对系统的对称性起着关键作用,通过保持或调整系统在PT反演下的对称性,影响波函数、自旋翻转等量子行为,并决定系统的响应和性质。通过研究和理解对称势函数的特性,可以揭示它在系统行为中的影响,探索基于PT对称势的非线性薛定谔方程中的新的物理现象,例如新的能级结构、非线性激发和相互作用机制等,这对于发现和理解量子系统的新特性具有重要意义。此外,对称势函数的研究还有助于在材料设计和工程领域中找到具有特定PT对称性的势函数。这些设计可以用于调控光、声、电场和自旋等在材料中的传播和操控行为,为开发新型器件和应用提供理论基础。总之,理解和研究带有PT对称势的非线性薛定谔方程中的对称势函数对于深入理解系统行为、揭示潜在物理现象、指导材料设计和工程控制,并探索新的应用领域具有重要意义。下面我们探讨如何构建这个关于势函数的反问题,并且能够让这个势函数保持PT对称。
同构建关于散射–衍射系数反问题类似,如果当前可测量到部分光束数据,并且NLSE方程中的散射–非线性系数已知,我们想寻找合适的势函数满足这个光束的传播。即假设N个测量点
处的测量数据,以及NLSE方程(1)~(2)中色散系数
,非线性系数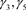 都是已经已知,我们的目标是寻找满足PT对称的势函数
,使得计算得到的数据
都是已经已知,我们的目标是寻找满足PT对称的势函数
,使得计算得到的数据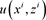 与已知测量数据
与已知测量数据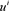 之间的差异最小。
之间的差异最小。
可将优化问题表示如下:
(4)
需要注意的是,与求解散射–衍射系数反问题(3)的情况不同,求解势函数反问题(4)时,我们需要确保势函数满足PT对称性。这样的限制条件使得问题更加复杂,需要使用合适的优化算法和策略来确保所得到的势函数具有所需的对称性。
下面我们将讨论如何对这两类反问题进行求解。
3. 两类反问题的求解
为了方便对散射–衍射系数反问题(3)和势函数反问题(4)进行求解,我们先根据NLSE方程(1)来构建一个新的函数。将复波函数u分解为实部p和虚部q,让
,其中
和
都是实值函数。引入一个隐函数
,定义函数
如下:
(5)
其中,隐函数 (
,
分别表述实部和虚部)。又令
(
(
,
分别表述实部和虚部)。又令
( )满足:
)满足:
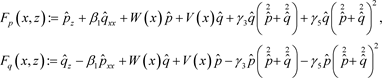
针对NLSE的均方误差损失函数

由于
满足薛定谔方程,即
,
。进一步考虑到部分样本点
位于边界上,记这些点为 ,因为(1)是周期性边界条件,则有
。即构造损失函数如下:
,因为(1)是周期性边界条件,则有
。即构造损失函数如下:
(6)
其中
 表示
上时空区域内被采样N个点;
表示采样点中NB边界数据采样点;内部残差项
计算内部点的损失,
方程偏差项
计算方程误差,边界条件偏差项
计算边界点的损失。
表示
上时空区域内被采样N个点;
表示采样点中NB边界数据采样点;内部残差项
计算内部点的损失,
方程偏差项
计算方程误差,边界条件偏差项
计算边界点的损失。
将原来(3)和(4)提出的反问题,转化为求解损失函数TL的最小值。得(3)对应的反问题
(7)
(4)对应的反问题
(8)
通过最小化损失函数(7),求出NLSE方程的参数
;通过最小化损失函数(8),求出NLSE方程的PT对称势函数
。当
(其中 是误差容限)时,输出预测值
或
(见图1),利用PINNs反演NLSE中PT对称势的参数的主要步骤如表1所示。
是误差容限)时,输出预测值
或
(见图1),利用PINNs反演NLSE中PT对称势的参数的主要步骤如表1所示。

Figure 1. PINNs deep learning framework for inverse problems of PT-symmetric potentials
图1. PINNs深度学习框架用于PT对称势场的反问题

Table 1. Learning or PT-symmetric potentials ϑ ( x ) in PINNs method (5)
表1. PINNs方法学习(5)中的
或PT对称势
3.1. 色散系数与非线性系数反演方法
对色散系数和非线性系数反问题使用PINNs求解,将
、
和未知解
代入损失函数(7)中,最终实现参数反演。
为比较PINNs方法和传统求解反问题方法的计算效率,我们下面给出了结合有限差分法求解正问题和使用粒子群算法进行优化的算法。我们在附录中提出了求解NLSE的有限差分法。下面介绍优化问题的PSO算法,即算法1。
PSO方法是由Marini F [16] 提出的,其主要思路如下:
假设目标搜索空间为D维,群体规模为M;第i个粒子的D维位置矢量为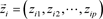 ,根据事先给定的适应值函数计算
当前的适应值;粒子i的飞行速度为
;粒子i迄今为止搜到的最优位置为
;设
为整个粒子群迄今为止搜索到的最优位置。在每次迭代中,粒子根据以下式更新速度和位置:
,根据事先给定的适应值函数计算
当前的适应值;粒子i的飞行速度为
;粒子i迄今为止搜到的最优位置为
;设
为整个粒子群迄今为止搜索到的最优位置。在每次迭代中,粒子根据以下式更新速度和位置:
式中:
;k为迭代次数;
为惯性因子;
和
为[0, 1]之间的随机数;
和
为学习因子。
在PSO结合有限差分算法中,只需将目标参数
作为优化参数即可。其中,Results可选择
最大
范数误差。
3.2. PT对称势函数反演方法
对PT对称势函数反问题,由于势函数与波函数u及其导数之间存在的高度非线性关系,使得直接反演势函数有一定困难。为了解决这个问题,我们提出了自适应基函数的PINNs算法。这个算法的核心是选择适当的基函数,使得神经网络模型能够更好地逼近复杂的解空间,提高对梯度信息的敏感度。
在PINNs中,基函数的选择需要根据对问题的理解和神经网络特性进行。对于PT对称势函数,考虑到其本身对称性要求,我们选择实部采用偶函数,虚部采用奇函数来作为基函数。这样既能有效覆盖解空间,又符合物理约束,有助于更好地捕捉势函数的特性。于是,令目标函数
,势函数
的基函数选取如下:
其中n的个数根据精度要求,采用自适应的原则选取。如果使用三角基函数无法达到理想的误差,我们可以在实部和虚部基函数中,分别引进两个激活函数,即sigmod函数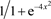 和双曲正切函数
。激活函数作为自适应函数能够通过引入非线性特性增强神经网络的表达能力,解决梯度消失问题,提高网络的稳定性和泛化能力,从而提高反演PT势函数的精确度。
和双曲正切函数
。激活函数作为自适应函数能够通过引入非线性特性增强神经网络的表达能力,解决梯度消失问题,提高网络的稳定性和泛化能力,从而提高反演PT势函数的精确度。
4. 数值例子
假设(1)的参数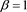 ,
和
,以及PT对称势选择
,
和
,以及PT对称势选择
则式(1)的精确解为:
根据精确解,我们在区域
内选取出测量数据。将解的实部和虚部分别表示为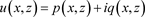 ,其中
和
由两个大小为256 × 201矩阵表示。这些采样点的数据
,其中
和
由两个大小为256 × 201矩阵表示。这些采样点的数据
存储在NLSE.mat文件中,以便导入到PINNs模型中。我们使用拉丁超立方体(LHS)采样策略生成模型训练所需的采样点数据,接下来以此为例子验证提出的两种反问题的求解方法。
4.1. 色散系数与非线性系数反演
首先考虑用PINNs和PSO结合附录中提出的有限差分法两种方法反演两个参数的情形。
在PINNs模型中,我们选取N个内部训练点,NB个边界训练点,网络是5个隐藏的层,每层有100个节点,如表2;粒子群算法的参数选取为
,
,
。表3比较了PINNs (
, )和PSO (
)两种方法反演非线性参数
和
通过运行时间和预测误差比较,我们可以得出PINNs物理信息神经网络快速寻找目标参数。
)和PSO (
)两种方法反演非线性参数
和
通过运行时间和预测误差比较,我们可以得出PINNs物理信息神经网络快速寻找目标参数。

Table 2. Under different values of N and NB, the prediction errors of γ 3 and γ 5 , as well as the training errors of p and q, loss function, and runtime
表2. 在不同的N和NB下
,
预测误差,以及p,q训练误差,损失函数和运行时间

Table 3. Comparison between PINNs and PSO algorithm simultaneous inversion of two parameters, where N = 81 and N B = 5
表3. PINNs与PSO算法比较:同时反演两个参数,其中
,
接下来用两种方法分别反演三个参数的情形。在PINNs模型中,我们选取N个内部训练点,NB个边界训练点,如表4。表5展示了我们利用PINNs (
,
)同时进行反演色散系数
和非线性参数
和
,预测误差仍能控制在10−3之内。但使用PSO (
)粒子群算法同时反演三个目标参数会导致陷入局部最优,无法寻找准确的目标参数。
在PINNs和传统方法解决NLSE反问题时,传统方法基于数学模型和物理定律,具有精确性和数学理论基础,但局限于简单两个以内参数反演问题和高计算复杂度,求解参数反问题时容易陷入局部最优问题;而PINNs不依赖特定数学模型,适用性广,计算效率高,虽然需要数据来训练模型,但灵活性和适应性更强,不易陷入局部最优。因此选择PINNs能更好地解决复杂非线性问题。

Table 4. Under different values of N and NB, the prediction errors of β , γ 3 and γ 5 , as well as the training errors of p and q, loss function, and runtime
表4. 在不同的N和NB下
,
,
预测误差,以及p,q训练误差,损失函数和运行时间

Table 5. Comparison between PINNs and PSO algorithm simultaneous inversion of three parameters, where N = 162 and N B = 10
表5. PINNs与PSO算法比较:同时反演三个参数,其中
,
4.2. PT对称势函数反演
根据章节3.2中提出的方法,构造PT对称势函数,(8)中
(9)
在不添加激活函数的情况下,我们采用自适应基函数选择方法。根据精度要求,基函数中的
,得到的计算结果在不同的N、NB情况下,6层网络,每层100个节点,如表6,其中
和
分别为PT对称势实部与虚部的最大误差。表7即为PT对称势最优情况下,自适应基函数系数。
图2为反演PT对称势函数的结果,其中图2(a)为实部和虚部绝对误差,误差分别达到10−2和10−3;图2(b) (左)为实部虚部预测值和真实值,图2(b) (右)为
绝对误差。可以看出反演的PT对称势最大误差0.011671,精度仅为10−2量级。这说明在自适应基函数选择方法中,仅使用三角函数作为基函数无法对PT势函数进行高精度反演,这与我们理想目标还存在一定差距。

Table 6. Under different values of N and NB, the prediction errors of and W 1 ( x ) , as well as the training errors of p and q, loss function, and runtime
表6. 在不同的N和NB下
和
预测误差,以及p,q训练误差,损失函数和运行时间

Table 7. PINNs operation (9) results of adaptive basis function coefficients, N = 810 and N B = 50
表7. PINNs运行(9)自适应基函数系数结果,
,
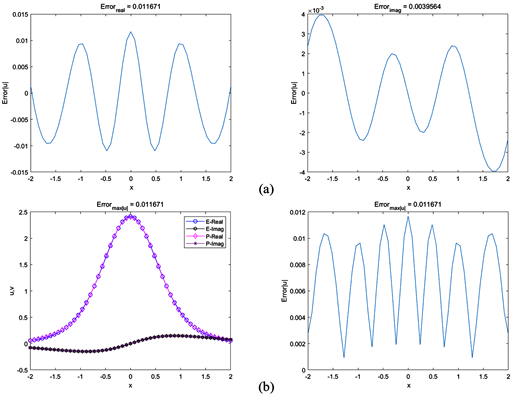
Figure 2. (a) Left: Real part prediction error; (a) Right: Imaginary part prediction error; (b) Left: Comparison between true and predicted values; (b) Right: Absolute error between true and predicted values
图2. (a)左为实部预测误差(a)右为虚部预测误差,(b)左为真实值和预测值比较(b)右为真实值与预测值的绝对误差
为进一步降低结果误差,使其绝对误差可以达到更小。接下来考虑加上激活函数,即(8)中
为
(10)
在添加激活函数的情况下,根据精度要求,选择基函数中的
,得到的计算结果在不同的N、NB情况下如表8。表9即为PT对称势最优情况下,自适应基函数系数。

Table 8. Under different values of N and NB, the prediction errors of V 2 ( x ) and W 2 ( x ) , as well as the training errors of p and q, loss function, and runtime
表8. 在不同的N和NB下
和
预测误差,以及p,q训练误差,损失函数和运行时间

Table 9. PINNs operation (10) results of adaptive basis function coefficients, N = 810 and N B = 50
表9. PINNs运行(10)自适应基函数系数结果,
,
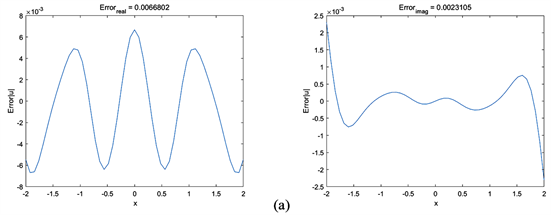

Figure 3. (a) Left: Real part prediction error; (a) Right: Imaginary part prediction error; (b) Left: Comparison between true and predicted values; (b) Right: Absolute error between true and predicted values
图3. (a)左为实部预测误差(a)右为虚部预测误差,(b)左为真实值和预测值比较(b)右为真实值与预测值的绝对误差
图3为反演PT对称势函数的结果。其中图3(a)为实部和虚部绝对误差,其误差都达到10−3。图3(b)为实部虚部预测值和真实值,以b(右)为
绝对误差。可以看出反演的PT对称势最大误差达到0.0066802,精度为10−3量级。这说明在自适应基函数选择方法中,使用三角函数和激活函数作为基函数对PT势函数可进行高精度反演,这与我们理想目标一致。
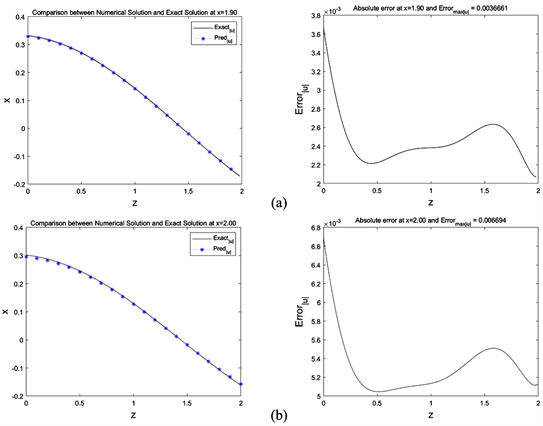
Figure 4. Absolute error between PINNs learned solution and exact solution of
and 2.00 for PT-symmetric potential from Table 9
图4. PINN学习解与表9中
和2.00处PT-对称势能的精确解之间的绝对误差
图4是在反演PT对称势(10)的情况,使用数据训练得到的PINNs学习解,可以看出,在我们所反演的PT对称势函数时,PINNs的学习解和数值解的绝对误差达到10−3。在未添加激活函数情况下(9)和在添加激活函数情况下(10)在PINNs运行程序结果数据选取和结果见表10所示。

Table 10. PINNs solution results for (1): N, NB, network layers, and runtime results
表10. PINNs求解(1)的N,NB,网络层数和运行结果
对于未添加激活函数的情况(表格中的表7),使用了810个数据点和100个边界点。神经网络的层数为
,这表示神经网络输入层和输出层各有2个节点、隐藏层一共有6层,每层含有100个节点。损失函数的数值为1.596e−04,表示模型在训练过程中能够较好地拟合目标函数。学习解与数值解在方程p和q上的绝对误差分别为2.894e−03和6.355e−03,这表示学习解与数值解在相应方程上的差异较小。方程势函数VPT的平方和误差为1.167e−02,这也说明学习解与数值解在整个方程系统上的拟合程度较好。运行时间为288.58s,表示训练模型所需的时间较短。
对于添加激活函数的情况(表9),使用了相同数量的数据点和边界点(810个数据点和100个边界点)。神经网络的层数仍为
,与未添加激活函数的情况相同。损失函数的数值略低,为1.530e−04,表明模型的拟合效果略好于未添加激活函数的情况。学习解与数值解在方程p和q上的绝对误差分别为1.613e−03和1.832e−03,说明学习解与数值解的差异较小。方程势函数VPT的平方和误差为6.795e−03,表明整体的拟合效果仍然较好。运行时间为307.97 s,与未添加激活函数的情况相比稍长一些。
综合上述分析,我们可以看出:
- 添加激活函数可以在一定程度上提高模型的拟合效果,减小损失函数的数值和方程误差;
- 不同的实验设置可能会对结果产生影响,比如数据点和边界点的数量、网络结构等;
- 在给定的实验条件下,使用的数据点和边界点数量相对较多,导致模型能够较好地拟合目标函数,但相应地运行时间也稍长。
需要注意的是,以上结论是基于给定表格中的数据进行分析的,具体结果可能因实验设置和数据集的不同而有所变化。因此,这些分析仅供参考,并需要进一步实验和验证。
5. 总结
在本文中,我们提出了带有PT对称势的NLSE的参数反演和势函数反演两类反问题,并采用PINNs方法求解。计算结果显示,PINNs具有较强的泛化能力,可以实现两类反问题的反演。
在对NLSE方程系数进行反演时,我们将PINNs方法和粒子群算法进行了比较。传统的PSO算法在每次更新参数时,都需要利用有限差分法重新求解一次NLSE方程,因此效率较低,计算速度慢。当需要反演的系数过多时,容易陷入局部最优解。而PINNs方法在求解反问题时比传统方法要快,因为它不需要反复计算NLSE方程的数值解,所需计算时间更短。PINNs还可以用于识别物理方程中的隐藏参数,以及分析不同参数之间的非线性依赖关系。
在反演具有PT对称性的势函数时,我们构造了带有自适应基函数的PINNs,该方法无需指定势函数的具体形式,也不依赖于任何先验模型。自适应基函数的选取使得PINNs能够在训练过程中自动调整基函数的形式,提高了反演PT势函数的精度和准确性,为光学领域中NLSE反问题研究提高了新的思路和方法。未来,我们还可以对PINNs算法进行存在性、唯一性、收敛性和稳定性分析,并利用PINNs算法求解更高维或更高阶的NLSE反问题。
附录
下面给出带有初边值条件的NLSE方程(1)的有限差分格式。
为了用差分格式求解(1)~(2),将求解区域
作剖分,取正整数
。将
作M等分,将
作N等分。
,
;
,
;
,
;
,
,
,记
,
,令

记
设
,引进如下记号:
记
设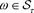 引进如下记号:
引进如下记号:
设
为
上的网格函数,则
为
上的网格函数, 为
上的网格函数。
为
上的网格函数。
在点
处考虑(1),于是有
(11)
由泰勒公式展开
(12)
(13)
由微分公式可得
(14)
其中
可以通过方程(1)结合初值条件(2)可求得。在点
处考虑(1),有
(15)
将(12)和(13)代入(15)中,可得
(16)
由初边值条件(2),并且忽略(14)和(16)小量项,对问题(1)~(2)建立如下线性差分格式
(17)
首先根据初始和边界条件计算
的值,记
由初值条件可知第0层上的值
,根据差分格式
则关于第1层值的差分格式为
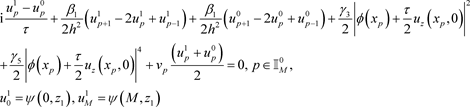 (18)
(18)
在(18)中,将第1层写在方程左边,第0层写在方程右边,令
可写成如下矩阵形式
求解以上代数系统,可以得到关于u的第1层数值解 。其中
。其中 通过 结合初值条件可求得。
通过 结合初值条件可求得。
计算出
后,接下来我们建立u的三层格式。假设已确定出了第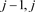 层的值
。根据差分格式为
层的值
。根据差分格式为
则关于第
层值的差分格式为

令
将第 层写在方程左边,
层及j层写在方程右边,可写成如下矩阵形式
层写在方程左边,
层及j层写在方程右边,可写成如下矩阵形式
(19)
由此我们得到求解本文中NLSE方程的有限差分格式,格式中步长取值越小,数值解越精确。