二次场算法对于可控源电磁地形问题的适用性研究

Research on the Applicability of Secondary Field Algorithm to Terrain Problems of Controlled-Source Electromagnetic Method

摘要: 二次场算法常用于处理平坦地形下的可控源电磁正演问题，在海洋可控源领域也得到了广泛的应用。而关于二次场算法能否处理陆地起伏地形区域尚无定论。本文介绍了基于二次场的可控源三维正演算法在起伏地形模型下的建立过程和使用原理。通过电磁理论分析和多种模型的计算实例，分析了二次场算法在地形区域的正演结果异常及其产生的原因。最后通过对模型电导率和离散网格的控制变量实验，验证了二次场算法在地形区域的正演结果异常暂时无法通过有效手段解决。结果表明，在地空模型条件下，二次场正演算法暂时无法适用于绝大部分的起伏地形区域。

Abstract: The secondary field algorithm is often used to deal with the forward modeling of Controlled- Sources Electromagnetic Method in flat terrain, and has also been widely used in the field of Marine Controlled-Sources Electromagnetic Method. However, there is still no conclusion on whether the secondary field algorithm can deal with the terrain region. In this paper, the establishment process and application principle of 3D forward modeling algorithm based on secondary field are introduced. Through the analysis of electromagnetic theory and calculation examples of various models, the forward results of secondary field algorithm in terrain region are analyzed and the causes are analyzed too. Finally, through the control variable experiments of the model conductivity and the discrete grid, it is verified that the forward anomaly of the secondary field algorithm in the terrain region cannot be solved by effective means. The results show that the secondary field algorithm cannot be applied to most of the undulating terrain regions under the condition of ground-air model.

1. 引言

可控源电磁法(CSEM)是克服了天然场源信号随机性的一类人工源电磁勘探方法，具有观测范围广、数据信噪比高等优点，近年来发展迅速，且在深部资源勘探和海洋油气勘探等领域得到了广泛的应用 ‎[1] ‎[2] 。然而CSEM三维反演的发展受限于起伏地形的影响而进步缓慢，以至于现有的资料解释技术已无法满足现实需求。正演是研究反演的基础，能否进行高效、高精度的正演模拟也是三维可控源电磁法正反演是否能够处理复杂地质结构的关键所在 ‎[2] 。

在CSEM三维正演求解的过程中，右端源项的处理是提高正演精度的关键所在。由于源项的加载是否正确以及场源奇异性问题会严重影响方程右端项的积分，因此如何进行源的处理是正演算法的重中之重。目前常用的处理源的办法主要有两种 ‎[2] ：一是基于总场算法，并采用伪函数来加载源项，以此解决源的奇异性问；二是基于二次场算法，即将正演模型分解为背景模型和异常体，先对背景模型下的一次场进行求解，再计算异常体在一次场影响下产生的二次。二次场算法具有很高的应用价值，其通过一次场与二次场分解避免了源附近的快速场变。且二次场算法仅需对背景模型下的异常体进行网格离散计算，并将二次场的计算结果和一次场的解析解相加，这也使二次场方法可能产生更精确的结果。但由于二次场算法需要计算选定背景模型的一次场，当背景模型过于复杂时，这一步可能消耗过多的计算资源。因此，在目前只有一些简单的地电模型存在解析表达式的条件下，二次场算法只有在一些特殊情况下才能得到广泛的应用。

目前，关于复杂地形下是否能使用二次场方法进行数值模拟获得可靠的结果尚无定论。Alumbaugh (1996)指出，如果源位于地形区域，则二次场偏微分方程中等效源项内的一次场快速变化可能导致计算精度出现问题。同样，Mitsuhata (2000)和Streich (2009)指出，需要选择合适的背景场，以使二次场的源不会出现在一次场的源附近。这一条件会对二次场算法的适用性造成限制，因为现场测量中通常会观察到电偶极子源附近的小尺度异常，并导致在接收点记录的电磁场出现失真现象 ‎[3] ‎[4] 。

由于目前仅存在均匀半空间和水平层状介质模型的解析解或半解析解，如果基于二次场建立方程组进行计算，需要划分出合适的背景模型，以此建立由一次场和异常体共同组成的源项。当地表存在起伏地形时，无法在原模型的背景下求出一次场的解析解，需要重新划分地空分界面建立均匀半空间或水平层状介质模型，并将地形部分视为异常地形加入源项。由于源项中的一次场可解析获得，异常地形的相关参数以及和测点的空间关系将极大地影响数值模拟的精度。因此，目前二次场算法在起伏地形下的适用性尚存在争议。本文旨在通过理论推导与数值模拟，分析起伏地形下二次场算法的可靠性与适用范围，为起伏地形下正演算法的选择提供参考结论 ‎[5] 。

2. 二次场正演算法基本理论

二次场正演算法的建立过程可以总结成以下三个步骤：1) 建立二次场的偏微分方程；2) 划分出合适的背景电导率及其地空分界面，建立均匀半空间或水平层状介质模型作为背景模型，求出一次场解析解；3) 将一次场解析解代入方程中进行有限元分析和离散化处理，组合矩阵求解线性方程组。

2.1. 二次场正演算法的偏微分方程

根据麦克斯韦方程组，假定时间因子，在各向同性介质中，电场E与磁场H满足如下关系式：

$\nabla \times E=i\omega \mu H$ (1)

$\nabla \times H-\left(\sigma -i\omega \epsilon \right)E=J_s$ (2)

其中，表示角频率(rad/s)，为介质磁导率，为介质电导率，为介质介电常数，为电流密度。如果通过公式(1)建立有限元的离散方程组，则需要对电场与磁场进行一致的离散化处理。因此，可以将公式(1)两边同时取旋度并代入公式(2)，以此消去磁场，得到电场的双旋度方程 ‎[6] ‎[7] ：

$\nabla \times \nabla \times E-\omega \mu \left(\omega \epsilon +i\sigma \right)E=i\omega \mu J_s$ (3)

通常情况下，如果采用电偶极子作为发射源，则电场在源所在的位置存在奇异性。如果直接计算总场，则需要在源的周围加密网格以应对电场在该区域的快速变化。为降低计算成本，消除源的奇异性，可以将电场分解为一次场(背景场)和二次场(散射场)：

$E=E_p+E_s$ (4)

由此，可以通过同样的方式得到一次场的双旋度方程：

$\nabla \times \nabla \times E_p-\omega \mu \left(\omega \epsilon +i{\sigma }_p\right)E_p=i\omega \mu J_s$ (5)

该式中，为一次场的背景电导率。由于在CSEM中通常满足的条件，此时忽略位移电流，并将公式(5)与公式(3)相减，整理后得到二次场满足的双旋度方程：

$\nabla \times \nabla \times E_s-i\omega \mu \sigma E_s=i\omega \mu \text{Δσ}{E}_p$ (6)

$\text{Δ}\sigma =\sigma -{\sigma }_p$ (7)

其中为异常电导率分布，即总电导率分布与背景电导率分布的差值。如果满足均匀半空间或水平层状介质的电导率分布，则可以通过快速汉克尔变换计算得出解析解。在物理意义上，公式(6)可视为电导率为的等效散射体在背景场作用下产生的散射电场所满足的偏微分方程组。即通过这种方法，可以将二次场视为异常电导率在一次场作用下的散射场，这样右端源项就由已知的一次场和异常电导率构成，消除了电偶源引起的奇异性以及网格剖分问题。

对于公式(6)，如果基于此方程构建正演算法，当边界距离正演研究区域足够远时，二次场可近似为0。因此，采用狄利克雷边界条件：

$n\times E|{}_{\partial \Omega }$ (8)

通过以上公式，可对二次场的偏微分方程进行有限元离散化处理，得出各节点的二次场值。再通过与已知的一次场相加得到总场值 ‎[8] ‎[9] ‎[10] 。

2.2. 有限元分析与线性方程组的求解

对求解区域进行非结构化四面体网格的剖分处理，采用伽辽金矢量有限单元法 ‎[3] 对方程(6)进行离散。设残差为R，则：

$R=\nabla \times \nabla \times E_s-i\omega \mu \sigma E_s-i\omega \mu \text{Δσ}{E}_p$ (9)

定义 $E_s\in H(curl,\Omega )$ ， $H\left(curl,\Omega \right)=\left\{V\in L^2\left(\Omega \right),\nabla \times V\in L^2\left(\Omega \right)\right\}$ 为矢量Hilbert空间， $L^2$ 为平方可积

函数，在空间内的内积定义为：

${\Vert v\Vert }_{L^2,\Omega }={\displaystyle {\iiint }_{\Omega }{\left|v\right|}^{2}dv},\Omega \subset R^3$ (10)

${\Vert v\Vert }_{L^2,F}={\displaystyle {\iint }_F{\left|v\right|}^{2}ds},F\subset \partial \Omega \subset R^2$ (11)

用矢量测试函数 $V\in H(curl,\Omega )$ 与公式(9)进行矢量点乘并应用第一矢量格林恒等式进行化简，得到：

$B\left(E_s,V\right)=D\left(V\right)$ (12)

$B\left(E_s,V\right)={\displaystyle {\iiint }_{\text{Ω}}\left(\nabla \times E_s\cdot \nabla \times V-i\omega \mu \sigma E_s\cdot V\right)dv}+{\displaystyle {\iint }_{\partial \text{Ω}}V\cdot \left(-\hat{n}\times \nabla \times E_s\right)ds}$ (13)

$D\left(V\right)={\displaystyle {\iiint }_{\text{Ω}}V\cdot i\omega \mu \text{Δ}\sigma E_{p}dv}$ (14)

设电导率在子单元内为常数，未知数置于四面体边单元上。使用一阶矢量基函数表示子单元内的电场：

$E_s=\underset{i=1}{\overset{6}{{\displaystyle \sum }}}{E}_{si}{N}_i$ (15)

应用经典伽辽金有限元法，将形函数N设置为测试函数V并得到如下表达式：

${\displaystyle {\iiint }_{\text{Ω}}\left(\nabla \times E_s\cdot \nabla \times N-i\omega \mu \sigma E_s\cdot N\right)dv}={\displaystyle {\iiint }_{\text{Ω}}N\cdot i\omega \mu \text{Δ}\sigma E_{p}dv}$ (16)

对上式进行离散化处理并合成求解矩阵，采用Pardiso直接求解器进行求解并将结果与一次场解析解相结合，即可得到求解区域内各点的电磁场数值解 ‎[11] ‎[12] 。

2.3. 精度验证

Figure 1. Schematic diagram of block low resistance anomalous body model

图1. 块状低阻异常体模型示意图

为验证算法的数值解精确度，设置如图1所示的块状低阻异常体模型。其中空气层电导率和地层背景电导率分别设置为1 × 10⁻⁸ S/m和0.02 S/m；异常体的尺寸为120 m × 200 m × 400 m，中心点坐标为(1000 m, 0 m, 300 m)，电导率为0.2 S/m；沿x轴正方向布置一条长100 m的长导线源，发射电流为1 A，频率为3 Hz；沿x轴方向布置一条从(400 m, 0 m, 0 m)到(1400 m, 0 m, 0 m)的测线。该模型来自于Ansari和Farquharson (2014)，将本算法的计算结果与该篇文章中的计算结果进行比较，结果如图2所示。根据计算，本算法的计算结果与Ansari和Farquharson (2014)的计算结果在各测点的平均相对误差为0.91%，且在每一个测点上的相对误差均低于3.5%，展示了本算法较高的精度 ‎[13] ‎[14] 。

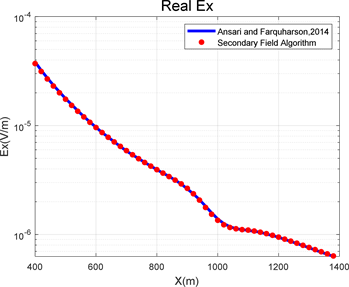
Figure 2. The comparison between the calculation results of the secondary field algorithm and those of Ansari and Farquharson (2014)

图2. 二次场算法与Ansari和Farquharson (2014)的计算结果对比图

3. 二次场算法误差产生的原因及其规律

对于一个存在凸起地形的地空模型，假定地层电导率为 ，空气层电导率为 。根据方程(6)，设平坦地面为背景场模型的地空分界面，则在地形区域方程右端的等效电流密度 可表示为：

$\text{Δσ}{E}_p=\left({\sigma }_n-{\sigma }_{air}\right)E_p$ (17)

其中， $E_p$ 可视为背景模型在激发源作用下的一次场。由于空气层在通常情况下可被视为绝缘体，因此在正演模拟中 ${\sigma }_{air}$ 通常被设置为1 × 10⁻⁸ S/m或更低的数值，且满足 ${\sigma }_{air}\ll {\sigma }_n$ 。对于 的计算而言， ${\sigma }_{air}$ 作为背景电导率的数值过小，在与 ${\sigma }_n$ 的差值计算中容易被忽略。考虑到一次场强度包含空气层的影响且在空气层范围内的数值非常低，在这种条件下，式(17)的等效电流密度 $\text{Δσ}{E}_p$ 计算过程中容易出现误差。由

于地形区域作为等效散射源且存在大量的电荷聚集，当测点位于地形上时，快速变化的电场也会对计算的精度做出更高的要求。

为研究二次场算法在不同的起伏地形模型下的适用性，本文将以总场算法3D有限元正演程序(Liu, 2022)的计算结果作为标准和对照，该程序由总场方程建立有限元方程组，适用于模拟各种复杂地形条件下的电磁数据 ‎[15] 。采用非结构化的四面体网格对求解模型进行离散化处理，利用最长边二分法在测点区域生成自适应加密的四面体网格，并通过并行迭代求解器对最后的大规模线性方程组进行求解。为确保实验的严谨性，部分模型会在高频和低频两种情况下进行计算。其中高频条件下的模型各项参数为：100 m长导线源中心点坐标(50 m, 0 m, 0 m)，发射电流1 A，频率1000 Hz，地层电导率0.02 S/m，空气电导率1 × 10⁻⁸ S/m；低频条件下的模型各项参数为：100 m长导线源中心点坐标(50 m, 0 m, 0 m)，发射电流1 A，频率3 Hz，地层电导率0.01 S/m，空气电导率1 × 10⁻⁸ S/m。

3.1. 地垒模型下二次场算法的误差分析

3.1.1. 正演模拟结果对比

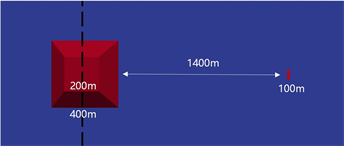
Figure 3. Schematic diagram of horst model

图3. 地垒模型示意图

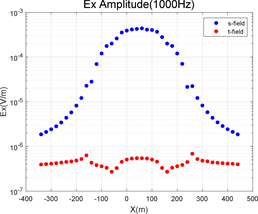(a)(b)

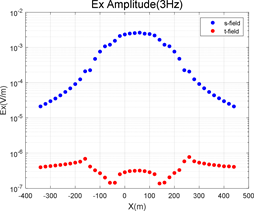
Figure 4. The results of the two algorithms are compared under the condition of high and low frequency

图4. 高低频条件下两种算法的计算结果对比

建立一个如图3所示的凸起地垒模型，其中地形高度为100 m，测线两端端点分别为(−340 m, 0 m, 0 m)和(440 m, 0 m, 0 m)且在地形区域沿地形布置，相邻测点的水平距离为20 m。在该模型下分别进行两种算法的正演计算并提取Ex振幅进行对比，结果如图4所示。观察Ex振幅曲线可知，二次场算法在地形及其周边区域的计算结果整体明显偏高。当测点位于地形上时，二次场算法的Ex振幅曲线整体呈隆起的拱形，即在起伏形态上也无法正确反映地形信息，且在x = 50 m ± 100 m和x = 50 m ± 200 m这四处明显的起伏地形分界点上也没有反映出正确的趋势。

将区域内网格单元的四个结点视电阻率值平均值作为该网格单元的视电阻率值，可获取两种算法下的地形区域网格单元视电阻率三维图，如图5、图6所示。该图可以更直观地体现出二次场算法在地空模型地垒地形区域的模拟效果。在高频条件下，二次场算法模拟结果的视电阻率分布在相邻网格之间的过渡更为平滑，图中颜色的变化更为均匀。这是由于二次场算法的结算结果是一次场的解析解和二次场的数值解的叠加，只需对异常电导率部分进行剖分计算，因此在条件合适的情况下可以达到更高的精确度。但在地垒区域，二次场算法的视电阻率计算结果出现明显的偏高情况，凸起地形部分出现严重的高阻异常，且该高阻异常向地形两侧方向呈扇形延伸。

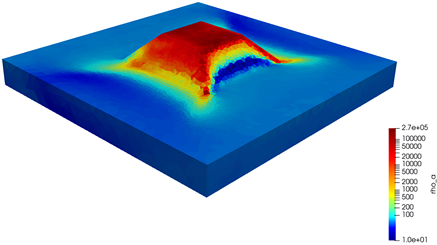
Figure 5. Three-dimensional apparent resistivity diagram of horst model under the secondary field algorithm

图5. 二次场算法下的地垒模型三维视电阻率图

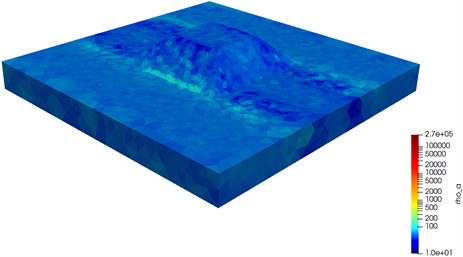
Figure 6. Three-dimensional apparent resistivity diagram of horst model under the total field algorithm

图6. 总场算法下的地垒模型三维正演视电阻率图

3.1.2. 电磁场分量对比

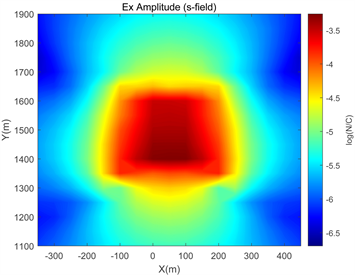
可以通过对电磁场在x，y方向上的分量来具体分析上述现象。建立xÎ[−350 m, 450 m]，yÎ[1100 m, 1900 m]的测量区域，沿x方向布置17条测线，其中相邻测线和同一测线的相邻测点之间的水平距离均为50 m。通过两种算法分别提取各个测点的Ex和Hy值，以高频条件下的计算结果为例，如图7、图8所示。

(a)(b)

Figure 7. Comparison of Ex components under two algorithms

图7. 两种算法下的Ex分量对比

观察各分量的对比可知，在本次实验中的地垒模型及各项参数下，电磁场各分量在测区范围内的二次场算法正演结果均严重偏高，且在中部地形区域最为明显。即二次场算法下电磁场各分量的正演结果均出现了从地形区域向四周扩散的明显异常。这一结果与3.1.1.的电场幅值与视电阻率正演结果相符，即地形在二次场算法下形成的等效散射区域会对周围测点的电磁场各分量正演结果产生严重的干扰。

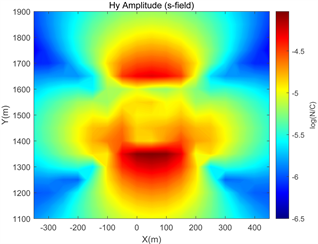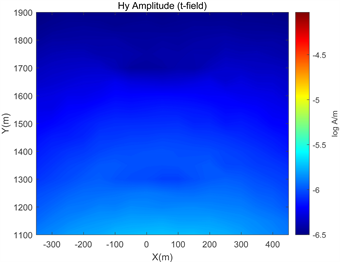(a)(b)

Figure 8. Comparison of Hy components under two algorithms

图8. 两种算法下的Hy分量对比

4. 影响二次场算法在地形区域适用性的因素

根据上一章的实验内容，在陆地地形条件下，二次场算法会在背景电导率模型与实际模型差值产生的等效散射区域内对二次场进行离散计算，并将结果与一次场的解析解相加得到总场值。由此产生了从等效散射区域向其他区域扩散的明显异常。根据数值计算的原理，正演区域内的网格密度会显著影响数值模拟结果的精度；而在模型相关参数的设置上，考虑到二次场算法常用于海洋可控源电磁法的正演模拟计算，再结合对公式(17)的分析，合理推测介质的电导率数值会对二次场算法的正演精度产生较大的影响 ‎[12] ‎[13] 。下面将对以上影响因素进行综合分析，并得出二次场算法在地形区域是否适用的最终结论。

4.1. 网格单元密度对地形区域二次场算法的影响

针对如图3所示的地垒模型，设100 m长导线源中心点坐标为(50 m, 0 m, 0 m)，发射电流1 A，频率1000 Hz，地层电导率设为0.02 S/m，空气电导率设为1 × 10⁻⁸ S/m。在测量区域xÎ[−350 m, 450 m]，yÎ[1100 m, 1900 m]范围内的地表上沿x方向布置17条测线，相邻测线和同一测线的相邻测点之间的水平距离均为50 m。将除地垒区域外的地表所在平面视为背景模型的地空分界面，则地垒区域为等效散射区域。对地垒区域与测点周围的网格进行加密，如图9所示。用两种算法分别计算Ex振幅数值，以总场算法为标准值计算二次场算法在各个测点的平均相对误差MRE (Mean Relative Error)。结果表明，将区域内网格数量从53,143分别增加到99,831和275,325时，二次场算法的MRE从81.465分别提升到94.144和103.418。即随着地形区域的网格加密，二次场算法与总场算法结算结果的差距并未减小，反而出现了一定程度上的增加。

Figure 9. Grid subdivision of horst area

图9. 地垒区域网格剖分示意图

4.2. 介质电导率差对地形区域二次场算法的影响

Figure 10. Comparison of Ex amplitude forward modeling results of two algorithms when ${\sigma }_{air}=5\times {10}^{-4}\text{S/m}$

图10. ${\sigma }_{air}=5\times {10}^{-4}\text{S/m}$ 时两种算法的Ex振幅正演结果对比

二次场算法常用于海洋可控源电磁法的正演模拟计算，在海洋模型下，海底起伏地形可被视为水平层状介质背景模型下的二次场等效散射区域，异常电导率Δσ在数值上等于海底地层电导率与海水电导率的差值。由于海水的电导率较高，区别于作为绝缘体的空气层，不会导致Δσ的求解过程中出现有较大数量级差距的差值计算。因此，介质电导率的差值会对二次场算法的计算造成巨大的影响。为印证这一部分的猜想，在3.3.1的实验基础之上对如图3所示的地垒模型进行空气层电导率的修改，同时计算二次场算法在各测点上的平均相对误差。结果表明，随着空气层电导率设置的数值升高，在数量级上趋近于地层电导率的数值，二次场算法与总场算法的计算结果会逐渐靠近。以图10为例，经计算，对本模型而言，当σ_air设置为5 × 10⁻⁴ S/m时，两种算法的Ex振幅正演结果在各测点的平均差距可以控制在5%左右。考虑到空气作为绝缘体，将其电导率数值设置为5 × 10⁻⁴ S/m明显过高，且与地层电导率仅存在两个数量级的差距，这会导致实验模型与现实条件不符，影响实验结果的可靠性 ‎[14] ‎[15] 。

5. 总结

本文对基于二次场和总场的可控源三维正演算法在地形区域的计算结果进行对比，通过不同的起伏地形模型和正演参数，研究了二次场算法在地形区域产生误差的大小及其原因。最后根据网格和介质电导率的具体分析可知，在现有的条件下，二次场算法无法应用于地空模型下的地形区域。

在通常情况下，二次场正演算法主要应用于均匀半空间和水平层状介质的衍生模型，或者海底地形模型。这几种模型的共同点是：被视为异常体的区域——如地层中的异常体或者海水中的海底地形，其电导率和该区域的背景模型电导率不存在数量级上的差距，因此在二次场计算公式的建立过程中做电导率的差值计算不会产生较大的误差。对于地面地形模型，空气层电导率极小的数值会导致等效电流密的求取过程中产生的误差无法避免，因而也无法通过网格的调整解决这一问题。