分数布朗运动驱动的自排斥扩散的渐近行为与参数估计

Asymptotic Behavior and Estimation of Self-Repelling Diffusion Driven by Fractional Brownian Motion (fBm)

摘要: 在本文中，我们研究了Hurst指数的分数布朗运动驱动的自排斥扩散随机微分方程解的长时间行为以及当ν=0时θ最小二乘估计_θ^{^}，并讨论了_θ^{^}相合性和_θ^{^}_T-θ的渐进分布。

Abstract: In this paper, we consider a self-repelling diffusion driven by a fractional Brownian motion with Hurst index , , we prove asymptotic behavior of the solution and the strong consistent of _θ^{^} when ν=0, we also obtain the asymptotic distribution of _θ^{^}_T-θ.

1. 引言

分数布朗运动(Fractional Brownian Motion)是一种重要的随机过程，其理解和分析离不开数学中的数与代数概念。在分数布朗运动中，数学上的概念和工具发挥着关键作用，帮助更好地建模和描述具有长期记忆性质的现象。通过数学中的代数表达式和运算规则，我们可以推导出分数布朗运动驱动的随机微分方程解的一些性质。同时，数学统计中的概念和技巧也能够帮助处理和分析方程中的参数估计问题，从而深入研究方程的特性和行为规律。因此，数与代数在分数布朗运动驱动的随机微分方程的理论和应用中扮演着至关重要的角色，为探索提供了坚实的基础和有效的工具。

1992年，Durrett和Rogers [1] 提出了聚合物生长形状的模型，也称为布朗聚合物模型，对应的随机微分方程的结构如下：

$X_t=X_0+B_t+{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{s}f}}\left(X_s-X_u\right)\text{d}u\text{d}s,$

其中B是d维标的准布朗运动，f是满足利普希茨条件的连续函数。该模型是边缘(顶点)自交互随机漫步概念的连续模拟。在 $f\left(x\right)=g\left(x\right)x/\Vert x\Vert$ 和 $g\left(x\right)\ge 0$ 条件下，方程的解 $X_t$ 被Pemantle [2] 证实是一个连续的过程，这个轨道依赖型随机微分方程可以看作是聚合物成型的模型， $X_t$ 表示在时间t时聚合物末端所在的位置。如果对任意的 $x\in R^d$ ，函数f满足 $x\cdot f\left(x\right)\ge 0$ (换而言之，它更倾向于远离其之前到达过的位置)，则称方程的解为自排斥的。如果对任意的 $x\in R^d$ ，函数f满足 $x\cdot f\left(x\right)\le 0$ (换而言之，它更倾向于返回到其之前到达过的位置)，则称方程的解为自吸引的。值得注意的是，这种模型可以比拟为一个Ornstein-Uhlenbeck过程，因此，研究这类方程的渐近行为与参数估计是很有意义的。更多的研究可以参考Nualart和Peccati [3] ，Benaïm [4] 等。

受启发，我们考虑随机微分方程

$X_t^H=x+B_t^H+\theta {\displaystyle {\int }_0^t{\displaystyle {\int }_0^s{\left(1+r\right)}^3}}\text{d}{X}_r^H\text{d}s+\nu t$ (1)

其中 $X_0^H=0$ ， $B^H$ 为带有Hurst指数 $\frac{1}{2}\le H<1$ 的分数布朗运动， $\nu \in ℝ$ 。本文，将展开并证明下面的陈述：

(I) 假设 $\frac{1}{2}\le H<1$ ，定义 ${\xi }_{\infty }={\displaystyle {\int }_0^{\infty }\theta }{\left(1+r\right)}^3{\text{e}}^{-G\left(r\right)}\text{d}{B}_r^H$

并且定义 $J^H\left(n;\theta \right)=\left\{J_t^H\left(n;\theta \right),t\ge 0\right\}$ ， $n=0,1,2,\cdots$ 通过 $J_t^H\left(0;\theta \right):=\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{X}_t$ ，

$J_t^H\left(n;\theta \right):=\frac{\theta {\left(1+t\right)}^4}{4}\left(J_t^H\left(n-1;\theta \right)-\left({\xi }_{\infty }+\nu \right){\lambda }_{n-1}\right),n\ge 1$

其中 $X_t$ 为的解。然后，有

$J_t^H\left(n;\theta \right)\to \left({\xi }_{\infty }+\nu \right){\lambda }_n$ (2)

其中

${\lambda }_0=1,{\lambda }_n=\frac{3\times \left(2\times 3+1\right)\times \cdots \times \left(3n+n-1\right)}{4^n}$

在 $L^2$ 中，当t趋于无穷时，对每个 $n=0,1,2,\cdots$ 几乎处处成立。

(II) 在公式(1)中，设 $\nu =0$ 时，通过使用Hu和Nualart [5] 介绍的最小二乘估计方法，假设过程 $\left\{X_t^H,t>0\right\}$ 在连续情况下，得到 $\theta$ 的最小二乘估计量

${\hat{\theta }}_T=\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{X}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t},$

其中 $Y_t^H={\displaystyle {\int }_0^t{\left(1+r\right)}^3\text{d}{X}_r^H},t\ge 0$ 则：

1) $\hat{\theta }$ 是强相合的

2) ${\left(T+1\right)}^{3\left(H-1\right)}{\text{e}}^{G\left(t\right)}\left(\hat{\theta }-\theta \right)\to 2{\theta }^{1-H}\sqrt{H\Gamma \left(2H\right)}\frac{N}{{\xi }_{\infty }}$

当T趋向于无穷的时。

本文结构如下，在第2部分简要回顾一些关于分数Brown运动的基本理论和Malliavin积分以及最小二乘估计方法。第3部分，证明了上述结论(I)。第4部分，证明了上述结论(II)。

2. 预备知识

在本部分中，将介绍分数布朗运动的一些基本定义和结果，以及参数估计将用到的最小二乘估计方法。设 $0<H<1$ ，Hurst参数为H的分数布朗运动为连续Gaussian过程 $B^H=\left\{B_t^H,t\ge 0\right\}$ ，定义在 $\left(\Omega ,{\mathcal{F}}^H,P\right)$ 上使得 ${\mathcal{F}}^H$ 是一个由 $B^H$ 生成的 $\sigma$ -域。可以知道对于任意的 $t,s\ge 0$ Gaussian随机过程 $B^H=\left\{B_t^H,t\ge 0\right\}$ 满足

$E\left[B_t^H{B}_s^H\right]=\frac{1}{2}\left[t^{2H}+s^{2H}-{\left|t-s\right|}^{2H}\right],$

$E\left[B_t^H\right]=0$

当 $H=1/2$ ， $B^{1/2}$ 与标准布朗运动B重合。当 $H\ne \frac{1}{2}$ 时，分数布朗运动既不是半鞅也不是马尔科夫过程，这时无法使用鞅论中经典的Itô型随机分析，当然也很难直接在分数布朗运动驱动的随机微分方程的研究中使用。作为一个高斯过程，我们可以构造关于 $B^H$ 的变差随机积分。设 $\mathcal{H}$ 为示性函数 $1_{\left[0,t\right]},t\in \left[0,T\right]$ 生成的线性空间 $\mathcal{E}$ ，满足如下的内积形式：

${\langle 1_{\left[0,s\right]},1_{\left[0,t\right]}\rangle }_{\mathcal{H}}=\frac{1}{2}\left[t^{2H}+s^{2H}-{\left|t-s\right|}^{2H}\right]$

对于任意的 $s,t\in \left[0,T\right]$ 。当 $\frac{1}{2}<H<1$ 时可以给出 $\mathcal{H}$ 的形式如下：

$\mathcal{H}=\left\{\phi :\left[0,T\right]\to ℝ|{\Vert \phi \Vert }_{\mathcal{H}}^2={\alpha }_H{\displaystyle {\int }_0^T{\displaystyle {\int }_0^T\phi }}\left(t\right)\phi \left(s\right){\left|t-s\right|}^{2H-2}\text{d}s\text{d}t<\infty \right\}$

其中 ${\alpha }_H=H\left(2H-1\right)$ 。可以在 $\mathcal{E}$ 上定义一个线性映射 $\phi \mapsto B^H\left(\phi \right)$ ，映射的具体形式如下：

$1_{\left[0,t\right]}\mapsto B^H\left(1_{\left[0,t\right]}\right):={\displaystyle {\int }_0^T{1}_{\left[0,t\right]}}\text{d}{B}_s^H=B_t^H,t\in \left[0,T\right]$

其中 $T>0$ ，则有，这个线性映射是一个从 $\mathcal{E}$ 到 $B^H$ 生成的Gaussian空间的等距线性映射，并且它可以扩展到 $\mathcal{H}$ 。这里的线性映射是等距的指的是映射保持向量之间的距离不变，对于任意两个向量u和v，线性映射T满足 $\Vert T\left(u\right)-T\left(v\right)\Vert =\Vert u-v\Vert$ ，其中 $\Vert .\Vert$ 表示向量的范数或长度。这个线性映射也被称为关于 $B^H$ 的维纳积分，表示为

$B^H\left(\phi \right)={\displaystyle {\int }_0^T\phi }\left(t\right)\text{d}{B}_t^H$ (3)

其中对于任意的函数 $\phi \in \mathcal{H}$ 。如果对于任意的 $T>0$ ，上述的维纳积分都可以很好的表示，那么我们可以进一步定义如下的积分：

${\displaystyle {\int }_0^{\infty }\phi }\left(t\right)\text{d}{B}_t^H$

其中对于任意的函数 $\phi$ 满足

${\Vert \phi \Vert }_{\mathcal{H}}^2:={\alpha }_H{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }\phi }}\left(t\right)\phi \left(s\right){\left|t-s\right|}^{2H-2}\text{d}s\text{d}t<\infty$

因此，我们称公式(3)为广义维纳积分。

用 $\mathcal{S}$ 表示如下形式的光滑函数集：

$F=f\left(B^H\left({\phi }_1\right),B^H\left({\phi }_2\right),\cdots ,B^H\left({\phi }_n\right)\right)$ (4)

其中 $f\in C_b^{\infty }\left({ℝ}^n\right)$ (f和其所有导数函数都是有界的)并且 ${\phi }_i\in \mathcal{H}$ 。公式(4)的函数$ F $的导数算子 $D^H$ (Malliavin导数)被定义为

$D^{H}F={\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{\partial f}{\partial x_j}}\left(B^H\left({\phi }_1\right),B^H\left({\phi }_2\right),\cdots ,B^H\left({\phi }_n\right)\right){\phi }_j$

导数算子(derivative operator)是指将可微函数映射到其导数函数的线性算子。上述导数算子是一个从 $L^2\left(\Omega \right)$ 到 $L^2\left(\Omega ;\mathcal{H}\right)$ 的闭算子。若算子的定义域和共轭空间上的范数拓扑的交集是非空的，且该算子在该交集上连续，则称其为闭算子(closable operator)。我们用 ${\mathbb{D}}^{1,2}$ 表示 $\mathcal{S}$ 的闭包，通过如下的范数：

${\Vert F\Vert }_{1,2}:=\sqrt{E{\left|F\right|}^2+E{\Vert D^{H}F\Vert }_{\mathcal{H}}^2}$

发散积分 ${\delta }^H$ 是导数算子 $D^H$ 的伴随。也就是说，我们说 $L^2\left(\Omega ;\mathcal{H}\right)$ 中的随机变量u属于发散算子 ${\delta }^H$ 的域，用 $\text{Dom}\left({\delta }^H\right)$ 表示，如果

$E\left|{\langle D^{H}F,u\rangle }_{\mathcal{H}}\right|\le c{\Vert F\Vert }_{L^2(\; \Omega \; )}$

对于每一个 $F\in \mathcal{S}$ 。在这种情况下， ${\delta }^H\left(u\right)$ 由对偶关系定义

$E\left[F{\delta }^H\left(u\right)\right]=E{\langle D^{H}F,u\rangle }_{\mathcal{H}}$ (5)

对于所有的 $u\in {\mathbb{D}}^{1,2}$ 。则有 ${\mathbb{D}}^{1,2}\subset \text{Dom}\left({\delta }^H\right)$ 和

$\begin{array}{c}E{\left|\delta \left(u\right)\right|}^2={\alpha }_H{\displaystyle {\int }_0^T{\displaystyle {\int }_0^{T}E}}\left[u_s{u}_t\right]{\left|s-t\right|}^{2H-2}\text{d}s\text{d}r\\ +{\alpha }_H^2{\displaystyle {\int }_0^T{\displaystyle {\int }_0^{T}E}}\left[\left(D_x^H{u}_s\right)\left(D_y^H{u}_t\right)\right]{\left|s-y\right|}^{2H-2}{\left|t-x\right|}^{2H-2}\text{d}s\text{d}t\text{d}x\text{d}y\end{array}$ (6)

对于所有的 $u\in {\mathbb{D}}^{1,2}$ 。我们将使用符号

${\delta }^H\left(u\right)={\displaystyle {\int }_0^T{u}_s}\delta B_s^H$

表示过程u的Skorohod积分，并定义了不定Skorohod积分 ${\displaystyle {\int }_0^t{u}_s}\delta B_s^H={\delta }^H\left(u{1}_{\left[0,t\right]}\right)$ 。

最小二乘法的原理，假设线性回归模型的拟合方程为 $y=ax+b$ ，那么残差平方和(损失函数)可以定义为

$L={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y^i-\left(a{x}^i+b\right)\right)}^2}$

拟合目的是使残差平方和L尽可能地小，即实际值和预测值尽可能地靠近。根据高等数学中求极值的相关知识，通过对残差平方和L进行求导(对参数a和b进行求导)，导数为0时，该残差平方和将取极值，便可以得到对应参数的估计量。

设 $B^H=\left\{B_t^H,t\ge 0\right\}$ 是一个带有Hurst指数 $H\left(\frac{1}{2}\le H<1\right)$ 的一维分数布朗运动，定义在 $\left(\Omega ,{\mathcal{F}}^H,P\right)$ 上，使得 ${\mathcal{F}}^H$ 是一个由 $B^H$ 生成的 $\sigma$ 域。设 $X^H$ 是一个分数自排斥扩散，通过如下方程定义

$\text{d}{X}_t^H=\text{d}{B}_t^H+\theta \left({\displaystyle {\int }_0^t{\left(1+s\right)}^3}\text{d}{X}_s^H\right)\text{d}t+\nu \text{d}t,t\ge 0$ (7)

其中 $X_0^H=0$ ， $\nu \in R$ 和 $B_0^H=0$ 。定义核函数 $\left(t,s\right)\mapsto h_{\theta }\left(t,s\right)$ 通过

$h_{\theta }\left(t,s\right)=\{\begin{array}{l}1+\theta {\left(1+s\right)}^3{\text{e}}^{-G\left(s\right)}{\displaystyle {\int }_s^t{\text{e}}^{G\left(u\right)}}\text{d}u,t\ge s\\ 0,t<s\end{array}$

其中 $G\left(s\right)=\theta {\displaystyle {\int }_0^s{\left(1+s\right)}^3}\text{d}r=\frac{\theta {\left(1+s\right)}^4-\theta }{4}$ ，根据Yan和Sun [6] 方程(7)的解 $X_t^H$ 形式如下：

$X_t^H={\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}{B}_s^H+v{\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}s$ (8)

对于任意的 $s,t\ge 0$ 。

3. 长时间行为

假设 $\frac{1}{2}\le H<1$ ，此部分主要考虑由分数布朗运动驱动的自排斥扩散方程(7)的解

$X_t^H={\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}{B}_s^H+v{\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}s$

的渐近行为，其中 $X_0^H=0$ ， $\nu \in R$ 和 $B_0^H=0$ ，并得到了其有循环收敛性。

引理3.1：设 $\frac{1}{2}\le H<1$ ，定义过程

${\xi }_t^H:={\displaystyle {\int }_0^t\theta }{\left(1+r\right)}^3{\text{e}}^{-G\left(r\right)}\text{d}{B}_r^H,t\ge 0$

则，过程 ${\xi }^H=\left\{{\xi }_t^H,t\ge 0\right\}$ 和这个随机变量 ${\xi }_{\infty }^H:={\displaystyle {\int }_0^{\infty }\theta }{\left(1+r\right)}^3{\text{e}}^{-G\left(r\right)}\text{d}{B}_r^H$ 可以在 $L^2$ 上被定义，并且

${\eta }_t^H:={\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n\Psi \left(t\right)\left({\xi }_{\infty }^H-{\xi }_t^H\right)\to 0$

在 $L^2$ 上几乎处处收敛，当t趋向于无穷的时，对于所有的 $n\ge 0$ ，其中 $\Psi \left(t\right)=\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u$ 。

证明：当 $H=\frac{1}{2}$ 对应布朗运动情况，引理显然成立。当 $\frac{1}{2}<H<1$ ，随机变量 ${\xi }_{\infty }^H$ 定义在 $L^2$ 上，根据均值定理和连续性有

${\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_t^{t+x}\theta }{\left(1+r\right)}^3\text{d}r=x{\text{e}}^{-G\left(t\right)}\theta {\left(1+t+kx\right)}^3\le C_{H}x$

其中 $x\in \left[0,1\right]$ 和 $k\in \left[0,1\right]$ 。故

$\begin{array}{c}\text{d}s={\displaystyle {\int }_0^{+\infty }\theta }{\left(1+t+x\right)}^3{\text{e}}^{-G\left(t+x\right)}{x}^{2H-2}\text{d}x={\displaystyle {\int }_0^{+\infty }{x}^{2H-2}}\text{d}x\left({\text{e}}^{-G\left(t\right)}-{\text{e}}^{-G\left(t+x\right)}\right)\\ =\left(2-2H\right){\displaystyle {\int }_0^{+\infty }{x}^{2H-3}}\left({\text{e}}^{-G\left(t\right)}-{\text{e}}^{-G\left(t+x\right)}\right)\text{d}x\\ =\left(2-2H\right){\displaystyle {\int }_1^{+\infty }{x}^{2H-3}}\left({\text{e}}^{-G\left(t\right)}-{\text{e}}^{-G\left(t+x\right)}\right)\text{d}x+\left(2-2H\right){\displaystyle {\int }_0^1{x}^{2H-3}}\left({\text{e}}^{-G\left(t\right)}-{\text{e}}^{-G\left(t+x\right)}\right)\text{d}x\\ \le 1+\left(2-2H\right){\displaystyle {\int }_0^1{x}^{2H-3}}\left({\text{e}}^{-G\left(t\right)}-{\text{e}}^{-G\left(t+x\right)}\right)\text{d}x\\ \le 1+\left(2-2H\right){\displaystyle {\int }_0^1{x}^{2H-3}}{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_t^{t+x}\theta }{\left(1+y\right)}^3\text{d}y\text{d}x\le C_H\end{array}$ (9)

对于任意的 $t\ge 0$ 。运用洛必达法则，有

$\begin{array}{c}{\Lambda }_g\left(H\right):=\underset{t\to \infty }{\lim }{\text{e}}^{G\left(t\right)}{\displaystyle {\int }_t^{+\infty }{\displaystyle {\int }_s^{+\infty }\theta }}{\left(1+s\right)}^3\theta {\left(1+r\right)}^3{\text{e}}^{-G\left(s\right)-G\left(r\right)}{\left(r-s\right)}^{2H-2}\text{d}r\text{d}s\\ =\underset{t\to \infty }{\lim }{\displaystyle {\int }_t^{+\infty }\theta }{\left(1+s\right)}^3{\text{e}}^{-G\left(s\right)}{\left(s-t\right)}^{2H-2}\text{d}s\le C_H\end{array}$

其中 $\frac{1}{2}<H<1$ 和 $n\ge 0$ 。在 $L^2$ 上，当t趋向于无穷大时有 $\Psi \left(t\right)\to 1$ 。下面证明它以概率1收敛，通过分部积分法和洛必达法则

$\begin{array}{l}{\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n\left({\xi }_{\infty }^H-{\xi }_t^H\right)={\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n{\displaystyle {\int }_t^{\infty }\theta }{\left(1+s\right)}^3{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H\\ =-\theta {\left(1+t\right)}^3{\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n{\text{e}}^{-G\left(t\right)}{B}_t^H-{\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n{{\displaystyle \int }}_t^{\infty }{B}_s^H\left\{\theta 3{\left(1+t\right)}^2-{\left(\theta {\left(1+t\right)}^3\right)}^2\right\}{\text{e}}^{-G\left(s\right)}\text{d}s\stackrel{a.s.}{\to }0\end{array}$

其中 $\frac{1}{2}\le H<1$ ，当t趋向于无穷大时。

引理3.2：定义函数 $I_{\theta }\left(t\right):R_{+}\to R$ 通过

$I_{\theta }\left(t\right)=\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u-1$

如果 $\frac{1}{2}\le H<1$ ，随机变量 ${\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(t\right)\text{d}{B}_t^H$ 定义在 $L^2$ 上，并且

${\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\to {\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\left(t\to \infty \right)$ (10)

在 $L^2$ 上几乎处处成立。

证明：

$\begin{array}{c}\underset{t\to +\infty }{\lim }{I}_{\theta }\left(t\right){\left(1+t\right)}^4=\underset{t\to \infty }{\lim }{\left(1+t\right)}^4{\text{e}}^{-G\left(t\right)}\left(\theta {\left(1+t\right)}^3{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u-{\text{e}}^{G\left(t\right)}\right)\\ =\underset{t\to \infty }{\lim }{\left(1+t\right)}^4{\text{e}}^{-G\left(t\right)}\left(\theta {\left(1+t\right)}^3{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u-{\displaystyle {\int }_0^t\theta }{\left(1+u\right)}^3{\text{e}}^{G\left(u\right)}\text{d}u-1\right)\\ =\theta \underset{t\to \infty }{\lim }\frac{1}{{\left(1+t\right)}^{-4}{\text{e}}^{G\left(t\right)}}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left({\left(1+t\right)}^3-{\left(1+u\right)}^3\right)\text{d}u\\ =\theta \underset{t\to \infty }{\lim }\frac{1}{{\left(1+t\right)}^{-4}{\text{e}}^{G\left(t\right)}}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}{\displaystyle {\int }_u^{t}3}{\left(1+r\right)}^2\text{d}r\text{d}u\end{array}$

$\begin{array}{c}=3\theta \underset{t\to \infty }{\lim }\frac{1}{{\left(1+t\right)}^{-4}{\text{e}}^{G\left(t\right)}}{\displaystyle {\int }_0^t{\left(1+u\right)}^2}\text{d}u{\displaystyle {\int }_0^u{\text{e}}^{G\left(r\right)}}\text{d}r\\ =3\underset{t\to \infty }{\lim }\frac{1}{{\left(1+t\right)}^{-3}{\text{e}}^{G\left(t\right)}}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u=\frac{3}{\theta }\end{array}$

结合函数 $t\mapsto I_{\theta }\left(t\right)$ 的连续性，我们有

$\left|I_{\theta }\left(t\right)\right|\le C_{\theta }^1\frac{1}{{\left(1+t\right)}^4}$

对于任意的 $t\ge 0$ ，有

$E{\left({\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(s\right)\text{d}{B}_s\right)}^2={\displaystyle {\int }_0^{\infty }{I}_{\theta }}{\left(s\right)}^2\text{d}s<\infty$

和

$E{\left({\displaystyle {\int }_0^{\infty }{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\right)}^2={\alpha }_H{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_0^{\infty }{I}_{\theta }}}\left(s\right)I_{\theta }\left(r\right){\left|s-r\right|}^{2H-2}\text{d}r\text{d}s<\infty$

对于 $\frac{1}{2}\le H<1$ 。于是，可以得到

$\underset{t\to \infty }{\lim }E{\left({\displaystyle {\int }_t^{\infty }{I}_{\theta }}\left(s\right)\text{d}{B}_s\right)}^2={\displaystyle {\int }_t^{\infty }{I}_{\theta }}{\left(s\right)}^2\text{d}s=0$

$\underset{t\to \infty }{\lim }E{\left|{\Psi }_t\right|}^2=\underset{t\to \infty }{\lim }E{\left({\displaystyle {\int }_t^{\infty }{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\right)}^2={\alpha }_H{\displaystyle {\int }_t^{\infty }{\displaystyle {\int }_t^{\infty }{I}_{\theta }}}\left(s\right)I_{\theta }\left(r\right){\left|s-r\right|}^{2H-2}\text{d}r\text{d}s=0$

我们得到了公式(10)在 $L^2$ 上成立。

下面，证明对任意 $\theta >0$ ，当t趋向于无穷大时， ${\Psi }_t$ 几乎处处收敛到0，考虑函数 $t\mapsto {I^{\prime }}_{\theta }\left(t\right)$ ，有

$\begin{array}{c}{I^{\prime }}_{\theta }\left(t\right)=3\theta {\left(1+t\right)}^{21}{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u-{\theta }^2{\left(1+t\right)}^6{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u+\theta {\left(1+t\right)}^3\\ =\theta {\left(1+t\right)}^2{\text{e}}^{-G\left(t\right)}\left(3{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u-\theta {\left(1+t\right)}^4{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u+\left(1+t\right){\text{e}}^{G\left(t\right)}\right)\\ =\theta {\left(1+t\right)}^2{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left(3-\theta {\left(1+t\right)}^4+\theta \left(1+t\right){\left(1+u\right)}^3\right)\text{d}u+\theta {\left(1+t\right)}^3{\text{e}}^{-G(\; t\; )}\end{array}$

对于任意的 $t\ge 0$ 。设 $f_{\theta }\left(t\right)={\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left(3-\theta {\left(1+t\right)}^4+\theta \left(1+t\right){\left(1+u\right)}^3\right)\text{d}u$ ，对于任意的 $\theta >0$ ，我们可以得到 $f_{\theta }\left(0\right)=0$ ，

$\begin{array}{c}{f^{\prime }}_{\theta }\left(t\right)={\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left(-\theta \left(4\right){\left(1+t\right)}^3+\theta {\left(1+u\right)}^3\right)\text{d}u+3{\text{e}}^{G\left(t\right)}\\ =-4\theta {\displaystyle {\int }_0^{t}3}{\left(1+s\right)}^2\text{d}s{\displaystyle {\int }_0^s{\text{e}}^{G\left(u\right)}}\text{d}u+3\to -\infty \left(t\to +\infty \right)\end{array}$

并且对任意的 $t\ge 0$ ，有 ${f^{\prime }}_{\theta }\left(t\right)\le 3$ 。

因此

$f_{\theta }={\displaystyle {\int }_0^t{f^{\prime }}_{\theta }}\left(s\right)\text{d}s\to \infty \left(t\to +\infty \right)$

由洛必达法则，有

$\begin{array}{c}\underset{t\to +\infty }{\lim }{I^{\prime }}_{\theta }\left(t\right){\left(1+t\right)}^5=\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^7{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left(3-\theta {\left(1+t\right)}^4+\theta \left(1+t\right){\left(1+u\right)}^3\right)\text{d}u+\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^8{\text{e}}^{-G\left(t\right)}\\ =\theta \underset{t\to \infty }{\lim }\frac{{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left(3-\theta {\left(1+t\right)}^4+\theta \left(1+t\right){\left(1+u\right)}^3\right)\text{d}u}{{\left(1+t\right)}^{-7}{\text{e}}^{G\left(t\right)}}\\ =\underset{t\to \infty }{\lim }\frac{3{\text{e}}^{G\left(t\right)}+{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\left(-\theta \left(4\right){\left(1+t\right)}^3+\theta {\left(1+u\right)}^3\right)\text{d}u}{{\left(1+t\right)}^{-4}{\text{e}}^{G\left(t\right)}}\\ =\underset{t\to \infty }{\lim }\frac{-4\theta }{{\left(1+t\right)}^{-4}{\text{e}}^{G\left(t\right)}}\left({\displaystyle {\int }_0^{t}3}{\left(1+s\right)}^2\text{d}s{\displaystyle {\int }_0^s{\text{e}}^G}\left(u\right)\text{d}u\right)=-\frac{12}{\theta }\end{array}$

对于任意的 $\theta >0$ 。结合函数 $t\mapsto {I^{\prime }}_{\theta }\left(t\right){\left(1+t\right)}^5$ 的连续性，有

$\left|{I^{\prime }}_{\theta }\left(t\right)\right|\le C_{\theta }^2\frac{1}{{\left(1+t\right)}^5}$

对于 $t\ge 0$ 。由条件 ${\displaystyle {\int }_t^{\infty }{B}_s^H}{I^{\prime }}_{\theta }\left(s\right)\text{d}s\stackrel{a.s.}{\to }0$ ，当t趋向于无穷，结合均值定理有

$I_{\theta }\left(t\right)B_t^H\stackrel{a.s.}{~}\frac{4}{\theta {\left(1+t\right)}^4}{B}_t^H\stackrel{a.s.}{\to }0\left(t\to \infty \right)$

对于任意的 $\frac{1}{2}\le H<1$ 。因此，当t趋向于无穷大时

${\Psi }_t={\displaystyle {\int }_t^{\infty }{I}_{\theta }}\left(s\right)\text{d}{B}_s^H=-I_{\theta }\left(t\right)B_t^H-{\displaystyle {\int }_t^{\infty }{I^{\prime }}_{\theta }}\left(s\right)B_s^H\text{d}s\to 0$

几乎处处成立。

定理3.1：设 $\frac{1}{2}\le H<1$ ，通过以下方式定义递归过程 $J^H\left(n;\theta \right)=\left\{J_t^H\left(n;\theta \right),t\ge 0\right\}$ ， $n=0,1,2,\cdots$

$\begin{array}{l}{J}_t^H\left(0;\theta \right):=\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{X}_t,\\ J_t^H\left(n;\theta \right):=\frac{\theta {\left(1+t\right)}^4}{4}\left(J_t^H\left(n-1;\theta \right)-\left({\xi }_{\infty }+\nu \right){\lambda }_{n-1}\right),n\ge 1\end{array}$

其中 $X_t$ 是公式(8)，则

$J_t^H\left(n;\theta \right)\to \left({\xi }_{\infty }+\nu \right){\lambda }_n$ (11)

其中

${\lambda }_0=1,{\lambda }_n=\frac{3\left(2\ast 3+1\right)\cdots \left(3n+n-1\right)}{4^n}$

在 $L^2$ 几乎处处成立，对于每一个 $n=0,1,2,\cdots$ ，当t趋向于无穷大时。

证明：当 $n=0$ 时，我们有

$\begin{array}{l}\underset{t\to +\infty }{\lim }{J}_t^H\left(0;\theta \right)=\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{X}_t\\ =\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}\left[{\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}{B}_s^H+\nu {\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u\right]\\ =\underset{t\to +\infty }{\lim }\left[\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{h}_{\theta }}\left(t,s\right)\text{d}{B}_s^H+\nu \left(I_{\theta }\left(t;0\right)\right)\right]\\ =\underset{t\to +\infty }{\lim }\left[\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t\left[1+\theta {\left(1+s\right)}^3{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u-{\displaystyle {\int }_0^s{\text{e}}^{G\left(u\right)}}\text{d}u\right)\right]\text{d}{B}_s^H}+\nu \left(I_{\theta }\left(t;0\right)\right)\right]\end{array}$

$\begin{array}{l}=\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}\left[{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u{\displaystyle {\int }_0^t\theta }{\left(1+s\right)}^3{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H-{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\right]+\underset{t\to +\infty }{\lim }\nu \left(I_{\theta }\left(t;0\right)\right)\\ =\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{\text{e}}^{G\left(u\right)}}\text{d}u{\xi }_t-\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H+\underset{t\to +\infty }{\lim }\nu \left(I_{\theta }\left(t;0\right)\right)\\ =\underset{t\to +\infty }{\lim }{\xi }_t\left(I_{\theta }\left(t;0\right)\right)-\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H+\underset{t\to +\infty }{\lim }\nu \left(I_{\theta }\left(t;0\right)\right)\\ =\underset{t\to +\infty }{\lim }\left({\xi }_t+\nu \right)\left(I_{\theta }\left(t;0\right)\right)-\underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\end{array}$

从引理3.1和引理3.2，有

$\begin{array}{l}\underset{t\to +\infty }{\lim }{\xi }_t\to {\xi }_{\infty }\\ \underset{t\to +\infty }{\lim }\left({\xi }_t+\nu \right)I_{\theta }\left(t;0\right)=\underset{t\to +\infty }{\lim }\left({\xi }_t+\nu \right)\left[\theta {\left(1+t\right)}^3\left[{\displaystyle \underset{k=2}{\overset{k=n+1}{\sum }}{\left(-1\right)}^n}\frac{3\left(2\ast 3+1\right)\cdots \left(3k+k-1\right)}{{\theta }^{k+1}{\left(1+t\right)}^{3\left(k+1\right)+k}}\right]+1\right]\to {\xi }_{\infty }+\nu \\ \underset{t\to +\infty }{\lim }\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\to 0\end{array}$

在 $L^2$ 上几乎处处成立，则

$\underset{t\to +\infty }{\lim }{J}_t^H\left(0;\theta \right)\to \left({\xi }_{\infty }+\nu \right)$

对于n，

$\begin{array}{c}\underset{t\to +\infty }{\lim }{J}_t^H\left(n;\theta \right)=\underset{t\to +\infty }{\lim }\frac{\theta {\left(1+t\right)}^4}{4}\left(J_t^H\left(n-1;\theta \right)-{\lambda }_{n-1}\left({\xi }_{\infty }+\nu \right)\right)\\ =\underset{t\to +\infty }{\lim }\left({\xi }_t+\nu \right){\lambda }_n-\underset{t\to +\infty }{\lim }{\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\end{array}$

由引理3.2得

$\underset{t\to +\infty }{\lim }{\left(\frac{\theta {\left(1+t\right)}^4}{4}\right)}^n\theta {\left(1+t\right)}^3{\text{e}}^{-G\left(t\right)}{\displaystyle {\int }_0^t{I}_{\theta }}\left(s\right)\text{d}{B}_s^H\to 0$

在 $L^2$ 上几乎处处成立，则

$\underset{t\to +\infty }{\lim }{J}_t^H\left(n;\theta \right)\to {\lambda }_n\left({\xi }_{\infty }+\nu \right)$

在 $L^2$ 几乎处处成立。

4. 自排斥扩散的参数估计

假设 $\frac{1}{2}\le H<1$ ，回顾分数布朗运动驱动的自排斥扩散为

$\text{d}{X}_t^H=\text{d}{B}_t^H+\theta \left({\displaystyle {\int }_0^t{\left(1+s\right)}^3}\text{d}{X}_s^H\right)\text{d}t+\nu \text{d}t$

令 $\nu =0$ ，有

$\text{d}{X}_t^H=\text{d}{B}_t^H+\theta \left({\displaystyle {\int }_0^t{\left(1+s\right)}^3}\text{d}{X}_s^H\right)\text{d}t$ (12)

其中 $X_0^H=0$ 和 $B_0^H=0$ 。

本部分，研究方程(12)中参数 $\theta$ 的最小二乘估计，通过使用Y. Hu和D. Nualart [5] 建立的最小二乘方法，假设过程 $\left\{X_t^H,t>0\right\}$ 可以连续观察。定义 $Y_t^H={\displaystyle {\int }_0^t{\left(1+r\right)}^3}\text{d}{X}_r^H,t\ge 0$ ，可以将方程(12)改写成

$\text{d}{X}_t^H=\text{d}{B}_t^H+\theta \left(Y_t^H\right)\text{d}t$ (13)

使用常系数变异法，有

$Y_t^H={\text{e}}^{G\left(t\right)}{\displaystyle {\int }_0^t{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H$ (14)

设 ${\xi }_t={\displaystyle {\int }_0^t{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H$ ，故 $Y_t^H={\text{e}}^{G\left(t\right)}{\xi }_t$ 。参数 $\theta$ 的最小二乘估计量可以通过计算下面损失函数 $\rho \left(\theta \right)$ 的最小值获得

$\rho \left(\theta \right)={\displaystyle {\int }_0^T{\left(\stackrel{.}{X_t^H}-\theta Y_t^H\right)}^2}\text{d}t$

通过对损失函数 $\rho \left(\theta \right)$ 求导后等于零，有

${\hat{\theta }}_T=\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{X}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t},$

引理4.1：假设 $\frac{1}{2}\le H<1$ ，对于任意的整数 $p\ge 1$ ，有

${\left(1+T\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{2G\left(t\right)}}{\left({\xi }_t\right)}^p\text{d}t\to \frac{1}{2\theta }{\left({\xi }_{\infty }\right)}^p$ (15)

当T趋向于无穷大时。根据引理3.1，对于任意的 $m>0$ ， $\frac{1}{T^m}{\xi }_T\to 0$ 在 $L^2$ 几乎处处成立。

证明：当 $\frac{1}{2}\le H<1$ 时，由引理3.1，随机变量 ${\xi }_{\infty }$ 服从0均值正态分布，所以

$P\left({\xi }_{\infty }\ne 0\right)=1$

变量 $\left\{{\xi }_t,t\ge 0\right\}$ 连续，有 $\underset{t\to \infty }{\lim }\underset{\frac{1}{2}t\le s\le t}{\inf }{\xi }_s={\xi }_{\infty }$ ，因此，当t趋向于无穷大时 ${\displaystyle {\int }_0^t{\text{e}}^{2G\left(s\right)}}{\xi }_s^p\text{d}s\to \infty$ ，由洛必达法则， ${\left(1+T\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{2G\left(t\right)}}{\left({\xi }_t\right)}^p\text{d}t\stackrel{a.s.}{\to }\frac{1}{2\theta }{\left({\xi }_{\infty }\right)}^p$ 。

引理4.2：假设 $\frac{1}{2}\le H<1$ ，当T趋向于无穷大时

$\underset{T\to \infty }{\lim }{\left(T+1\right)}^{6H}{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)+G\left(r\right)}}}{\left|s-r\right|}^{2H-2}\text{d}s\text{d}r={\theta }^{-2H}\Gamma \left(2H-1\right)$

证明：对于非负连续函数f， $\underset{T\to \infty }{\lim }{\displaystyle {\int }_0^{T}f}\left(x\right)\text{d}x$ 存在且有限，有

$\underset{T\to \infty }{\lim }{\displaystyle {\int }_0^{T}f}\left(x\right)\frac{\text{d}x}{{\left(1-\frac{x}{{\left(1+T\right)}^4}\right)}^{\frac{3}{4}}}=\underset{T\to \infty }{\lim }{\displaystyle {\int }_0^{T}f}\left(x\right)\text{d}x$

根据洛必达法则和变量替换 $\frac{\theta }{4}\left({\left(1+T\right)}^4-{\left(1+r\right)}^4\right)=x$ 以及控制收敛定理，有

$\begin{array}{l}\underset{T\to \infty }{\lim }{\left(T+1\right)}^{6H}{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)+G\left(r\right)}}}{\left|s-r\right|}^{2H-2}\text{d}s\text{d}r\\ =2\underset{T\to \infty }{\lim }\frac{1}{{\left(T+1\right)}^{-6H}{\text{e}}^{2G\left(T\right)}}{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)}}{\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}{\left|s-r\right|}^{2H-2}\text{d}r\text{d}s\\ ={\theta }^{-1}\underset{T\to \infty }{\lim }{\left(1+T\right)}^{6H-3}{\displaystyle {\int }_0^T{\text{e}}^{-\frac{\theta }{4}\left({\left(1+T\right)}^4-{\left(1+r\right)}^4\right)}}{\left(T-r\right)}^{2H-2}\text{d}r\end{array}$

$\begin{array}{l}={\theta }^{-2}\underset{T\to \infty }{\lim }{\left(1+T\right)}^{6H-3}{\displaystyle {\int }_0^{G\left(T\right)}{\text{e}}^{-x}}{\left(T+1-{\left({\left(1+T\right)}^4-\frac{4x}{\theta }\right)}^{\frac{1}{4}}\right)}^{2H-2}\frac{\text{d}x}{{\left({\left(1+T\right)}^4-\frac{4x}{\theta }\right)}^{\frac{3}{4}}}\\ =\frac{4^{2H-2}}{{\theta }^{2H}}\underset{T\to \infty }{\lim }{\displaystyle {\int }_0^{G\left(T\right)}{\text{e}}^{-x}}{\left(1+{(1-\frac{4x}{\theta {\left(1+T\right)}^4})}^{\frac{1}{4}}\right)}^{2-2H}\frac{x^{2H-2}\text{d}x}{{\left(1-\frac{4x}{\theta {\left(1+T\right)}^4}\right)}^{\frac{3}{4}}}\\ ={\theta }^{-2H}\Gamma \left(2H-1\right)\end{array}$

引理4.3：设 $\frac{1}{2}\le H<1$ ，对于任意的 $\sigma \left\{B_t^H,t\ge 0\right\}$ -可测随机变量F满足 $P\left(F<\infty \right)=1$ ，当T趋向于无穷大时，有以下收敛成立

$\left(F,{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)}}\text{d}{B}_s^H\right)\to \left(F,\sqrt{H\Gamma \left(2H\right)}{\theta }^{-H}N\right)$ (16)

其中N是独立于 $B^H$ 的标准正态随机变量。

证明：对于任意 $T>0$ ，我们有

${\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)}}\text{d}{B}_s^H=N{\sigma }_{H,\theta }(\; T\; )$

其中“=”代表同分布，N是标准正态随机变量，并且

$\begin{array}{c}{\sigma }_{H,\theta }^2\left(T\right)={\left(T+1\right)}^{6H}{\text{e}}^{-2G\left(T\right)}E{\left({\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)}}\text{d}{B}_s^H\right)}^2\\ =H\left(2H-1\right){\left(T+1\right)}^{6H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)+G\left(r\right)}}}{\left|s-r\right|}^{2H-2}\text{d}s\text{d}r,T>0\end{array}$

根据引理4.2，有

${\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)}}\text{d}{B}_s^H\to \sqrt{H\Gamma \left(2H\right)}{\theta }^{-H}N,T\to \infty$

由方程(15)两侧服从二维正态分布，以及Hu和Nualart [5] ，只需要证明对于任意的 $d\ge 1$ ， $s_1,\cdots ,s_d\in \left[0,\infty \right)$ ，当T趋向于无穷大时，以下收敛成立

$\left(B_{s_1}^H,\cdots ,B_{s_d}^H,{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(s\right)}}\text{d}{B}_s^H\right)\to \left(B_{s_1}^H,\cdots ,B_{s_d}^H,{\theta }^{-H}\sqrt{H\Gamma \left(2H\right)}N\right)$ (17)

为了得到(15)，只需要证明其协方差矩阵收敛于相应的结果。当 $H=\frac{1}{2}$ ，显然，故以下考虑 $\frac{1}{2}<H<1$ 。对于任意固定的 $s>0$ ，有

$\begin{array}{l}E\left(B_s^H\cdot {\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(r\right)}}\text{d}{B}_r^H\right)\\ =H\left(2H-1\right){\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(v\right)}}\text{d}v{\displaystyle {\int }_0^s{\left|u-v\right|}^{2H-2}\text{d}u}\\ =H\left(2H-1\right){\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^s{\text{e}}^{G\left(v\right)}}\text{d}v{\displaystyle {\int }_0^s{\left|u-v\right|}^{2H-2}\text{d}u}\\ +H\left(2H-1\right){\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_s^T{\text{e}}^{G\left(v\right)}}\text{d}v{\displaystyle {\int }_0^s{\left|u-v\right|}^{2H-2}\text{d}u}\\ =:I\left(T\right)+J(\; T\; )\end{array}$

当 $T\to \infty$ ，我们有 $I\left(T\right)\to 0$ 。再根据洛必达法则，对任意的 $s>0$ ，有

$\begin{array}{c}0<J\left(T\right)=H{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_s^T{\text{e}}^{G\left(v\right)}}\left[v^{2H-1}-{\left(v-s\right)}^{2H-1}\right]\text{d}v\\ \le H{s}^{2H-1}\left({\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_s^T{\text{e}}^{G\left(v\right)}}\text{d}v\right)\to 0\end{array}$

则，对于任意的 $s>0$ ，有

$\underset{T\to \infty }{\lim }E\left(B_s^H\cdot {\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(r\right)}}\text{d}{B}_r^H\right)=0$

引理4.4：设 $\frac{1}{2}\le H<1$ ，当T趋向于无穷大时，有

${\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\delta B_s^H{\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}\delta B_r^H\stackrel{L^2}{\to }0$ (18)

${\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}s{\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}{\left|s-r\right|}^{2H-2}\text{d}r\to 0$ (19)

证明：方程(17)的收敛显然成立，下面考虑(18)的收敛性。通过二重积分的等距公式和方程(6)，对于任意 $T>0$ ，有

$\begin{array}{l}E{\left({\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}\delta B_r^H\right)\delta B_s^H\right)}^2\\ ={\left(T+1\right)}^{6H}{\text{e}}^{-2G\left(T\right)}E{\left({\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}\delta B_r^H\right)\delta B_s^H\right)}^2\\ ={\left({\alpha }_H\right)}^2{\left(T+1\right)}^{6H}{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}s{\displaystyle {\int }_0^s{\text{e}}^{G\left(x\right)}}\text{d}x{\displaystyle {\int }_0^T{\left(1+r\right)}^3}{\text{e}}^{-G\left(r\right)}\text{d}r{\displaystyle {\int }_0^r\text{d}}y{\text{e}}^{G\left(y\right)}\\ \times \left({\left|s-y\right|}^{2H-2}{\left|r-x\right|}^{2H-2}+{\left|s-r\right|}^{2H-2}{\left|x-y\right|}^{2H-2}\right)\end{array}$

再由不等式

${\displaystyle {\int }_0^s\text{d}}\xi {\displaystyle {\int }_0^r{\left|r-\xi \right|}^{2H-2}{\left|s-\eta \right|}^{2H-2}\text{d}\eta }\le \frac{2}{{\left(2H-1\right)}^2}{r}^{2H-1}{s}^{2H-1}$

则

$E{\left({\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}\delta B_r^H\right)\delta B_s^H\right)}^2\le C_H{T}^{2+6H}{\text{e}}^{-2G\left(T\right)}\to 0,T\to \infty .$

定理4.1：设 $\theta >0$ 且定理3.1的条件成立。对于 $\frac{1}{2}\le H<1$ ，当T趋向于无穷大时，有

${\hat{\theta }}_T=\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{X}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}\to \theta$

几乎处处成立。

证明：

$\hat{\theta }-\theta =\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{X}_t^H-\theta {\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}=\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}$

由分部积分，有

$\begin{array}{c}{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H=Y_T{B}_T^H-{\displaystyle {\int }_0^T{B}_t^H}\text{d}{Y}_t^H\\ =Y_T^H{B}_T^H-{\displaystyle {\int }_0^T{B}_t^H}\text{d}\left({\text{e}}^{G\left(t\right)}{\xi }_t\right)\\ =Y_T^H{B}_T^H-\theta {\displaystyle {\int }_0^T{\left(1+t\right)}^3}{\text{e}}^{G\left(t\right)}{B}_t^H{\xi }_t\text{d}t-{\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}{B}_t^H\text{d}{\xi }_t\\ =Y_T^H{B}_T^H-\theta {\displaystyle {\int }_0^T{\left(1+t\right)}^3}{\text{e}}^{G\left(t\right)}{B}_t^H{\xi }_t\text{d}t-{\displaystyle {\int }_0^T{\left(1+t\right)}^3}{B}_t^H\text{d}{B}_t^H.\end{array}$

根据方程(13)，引理3.1和洛必达法则，当T趋向于无穷大时，以下收敛以概率1成立：

$\begin{array}{l}{\left(1+T\right)}^{-3}{\text{e}}^{-G\left(T\right)}\cdot Y_T^H{B}_T^H=\frac{B_T^H}{{\left(1+T\right)}^3}\cdot {\text{e}}^{-G\left(T\right)}{Y}_T^H\to 0,\\ {\left(1+T\right)}^{-3}{\text{e}}^{-G\left(T\right)}\left({\displaystyle {\int }_0^T{\left(1+t\right)}^3}{\text{e}}^{G\left(t\right)}{B}_t^H{\xi }_t\text{d}t\right)\to 0\end{array}$

此外

$\begin{array}{c}{\left(1+T\right)}^{-3}{\text{e}}^{-G\left(T\right)}\cdot {\displaystyle {\int }_0^T{\left(1+t\right)}^3}{B}_t^H\text{d}{B}_t^H=\frac{1}{2}{\left(1+T\right)}^{-3}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+t\right)}^3}\text{d}{\left(B{t}^H\right)}^2\\ =\frac{1}{2}{\left(1+T\right)}^{-3}{\text{e}}^{-G\left(T\right)}\left[T{B}_T^H{}^2-{\displaystyle {\int }_0^T{B}_t^H{}^2}\text{d}t\right]\to 0\end{array}$

则

${\left(1+T\right)}^{-3}{\text{e}}^{-G\left(T\right)}\left({\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H\right)\to 0$

再由引理4.1，当 $p=2$ ，有

${\left(1+T\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t={\left(1+T\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{2G\left(t\right)}}{\left({\xi }_t\right)}^2\text{d}t\to \frac{1}{2\theta }{\left({\xi }_{\infty }\right)}^2$ (20)

所以

$\hat{\theta }-\theta =\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}\to 0$

当T趋向于无穷大。

定理4.2：假设 $\theta >0$ 和 $\frac{1}{2}\le H<1$ ，则

${\left(T+1\right)}^{3\left(H-1\right)}{\text{e}}^{G\left(t\right)}\left(\hat{\theta }-\theta \right)\to 2{\theta }^{1-H}\sqrt{H\Gamma \left(2H\right)}\frac{N}{{\xi }_{\infty }}$

依分布成立，其中N是独立的随机正态分布。

证明：对于任意的 $T>0$ ，有

${\left(T+1\right)}^{3(H-1)}{\text{e}}^{G\left(T\right)}\left(\hat{\theta }-\theta \right)={\left(T+1\right)}^{3\left(H-1\right)}{\text{e}}^{G\left(T\right)}\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}=\frac{{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H}{{\left(T+1\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}$

现在考虑渐近分布，对于任意的 $T>0$ ，有

$\begin{array}{l}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\text{d}{B}_t^H\right)\text{d}{B}_s^H\\ ={\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\delta B_t^H\right)\text{d}{B}_s^H\end{array}$

$\begin{array}{l}={\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\delta B_t^H\right)\delta B_s^H\\ +H\left(2H-1\right){\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}{\displaystyle {\int }_0^T{D}_r^H}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\delta B_t^H\right){\left|s-r\right|}^{2H-2}\text{d}s\text{d}r\\ ={\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\delta B_t^H\right)\delta B_s^H\\ +{\alpha }_H{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}{\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}{\left(s-r\right)}^{2H-2}\text{d}s\text{d}r.\end{array}$

所以，对任意的 $T\ge 0$ ，有

$\begin{array}{c}{\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}{\xi }_t\text{d}{B}_t^H={\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}\left({\displaystyle {\int }_0^t{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H\right)\text{d}{B}_t^H\\ ={\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}\left({\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H\right)\text{d}{B}_t^H-{\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}\left({\displaystyle {\int }_t^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\text{d}{B}_s^H\right)\text{d}{B}_t^H\\ ={\xi }_T{\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}\text{d}{B}_t^H-{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\text{d}{B}_t^H\right)\text{d}{B}_s^H\\ ={\xi }_T{\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}\text{d}{B}_t^H-{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\delta B_t^H\right)\delta B_s^H\\ -{\alpha }_H{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}{\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}{\left(s-r\right)}^{2H-2}\text{d}s\text{d}r.\end{array}$

当T趋向于无穷大，根据引理4.3和引理4.4，方程(19)收敛以及Slutsky定理，有

$\begin{array}{c}\frac{{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H}{{\left(T+1\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}=\frac{{\xi }_T{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\text{e}}^{G\left(t\right)}}\text{d}{B}_t^H}{{\left(T+1\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}\\ -\frac{{\left(T+1\right)}^{3H}{\text{e}}^{-G\left(T\right)}{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}\left({\displaystyle {\int }_0^s{\text{e}}^{G\left(t\right)}}\delta B_t^H\right)\delta B_s^H}{{\left(T+1\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}\\ -\frac{{(T+1)}^{3H}{\text{e}}^{-G\left(T\right)}{\alpha }_H{\displaystyle {\int }_0^T{\left(1+s\right)}^3}{\text{e}}^{-G\left(s\right)}{\displaystyle {\int }_0^s{\text{e}}^{G\left(r\right)}}{\left(s-r\right)}^{2H-2}\text{d}s\text{d}r}{{\left(T+1\right)}^3{\text{e}}^{-2G\left(T\right)}{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}\\ \to 2{\theta }^{1-H}\sqrt{H\Gamma \left(2H\right)}\frac{N}{{\xi }_{\infty }}\end{array}$

需要注意的是引理4.3表明随机变量N是相互独立的，从而证明了收敛性。

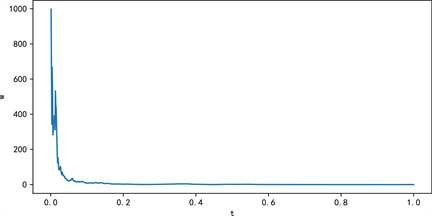
Figure 1. Numerical simulation of w tends to 0

图1. w趋于0的数值模拟

5. 数值模拟

对定理4.1中参数 $\theta$ 的估计量进行数值分析，即考虑下式

$w:=\hat{\theta }-\theta =\frac{{\displaystyle {\int }_0^T{Y}_t^H}\text{d}{B}_t^H}{{\displaystyle {\int }_0^T{\left(Y_t^H\right)}^2}\text{d}t}\to 0$

假设，步长数量 $n=1000$ ，Hurst指数 $H=0.7$ ，总时间 $T=1$ ，时间间隔 $\text{d}t=0.001$ 。

结果见图1。