1. 引言
新一轮科技革命和产业变革的到来以及可持续发展的理念指导下,各个国家均大力发展新能源汽车产业。新能源汽车的崛起不仅突破了传统汽车的局限,实现新一轮发展,还有助于汽车产业向更环保和更可持续的绿色化产业转型发展。在新能源汽车领域,永磁同步电机以其简单的结构和独特的工作方式而带来的更优异的输出转矩以及响应速度,成为了新能源汽车电机的首选 [1] 。然而,永磁同步电机在规避了传统电机中发动机的噪声的同时,随之而来的是永磁同步电机由于运行过程中电磁激振引起的振动噪声 [2] 。随着汽车产业的持续进步,对新能源汽车的标准和要求正在逐步提升,其中对于永磁同步电机的要求尤为严苛,在追求更高工作性能的同时,抑制其随之产生的电磁噪声成为学者的主要研究目标 [3] 。
秦臻等人 [4] 对新能源汽车永磁同步电机的振动噪声分类进行了研究,结果表明永磁同步电机的振动噪声主要来源于电磁噪声。周明浩 [5] 以60槽10极电机为研究对象,进行NVH仿真分析,结果表明,仿真结果与试验测试结果相符,为后续的NVH优化提供了参考。马功臣 [6] 对永磁同步电机中的定子冲片模态进行了模态分析,研究了可能共振的频率,为车用永磁同步电机的结构优化设计提供了指导。李民生 [7] 通过电磁振动联合仿真的研究策略,对电磁力进行了模拟计算,结合电机定子的模态参数仿真结果对定子进行了结构优化,结果表明,对定子的结构优化能够大幅降低振动幅值。邹良川 [8] 通过有限元分析法分析了电机的各个结构部件对电机耦合系统固有频率的影响。结果表明,永磁同步电机的机壳厚度对振动噪声的影响较其他结构部件更加明显。
本文利用三维建模软件Solidworks基于某汽车永磁同步电机实际参数简化建立电机模型。接着,通过有限元分析软件Ansys对电机的定子铁芯和外壳进行了模态分析,探讨了电机外壳厚度对模态频率的影响,在选取较合适的参数后,对电机整体进行了模态分析,分析了各部件装配后,对整体模态频率的影响。最后对电机外壳在电磁激振作用下的振动特性进行了仿真分析。
2. 几何模型建立
由于本文以结构分析为主,主要分析的是永磁同步电机的振动情况,在分析中主要是以主题结构部分为主,而其他部分的分析虽然能进一步提高模型分析的精确性却对结果影响不大,且太为复杂的模型会增加计算机分析时的计算量,降低分析效率。因此,在不影响仿真结果准确性的前提下,本文将电机结构简化为电机机壳、定子铁芯、绕组、转子、转轴等,表1为永磁同步电机的建模参数,使用SolidWorks 软件建立电机的三维模型,永磁同步电机模型如图1所示。
Figure 1. Schematic diagram of simplified model of terminal sheet metal part
图1. 永磁同步电机简化模型示意图
3. 模态分析
3.1. 模态分析概述
模态分析是近代科学研究结构动力特性的一种动态分析方法,广泛应用于结构设计领域和故障检测领域。研究表明:永磁同步电机的振动噪声与电机本身的固有频率以及振型密切相关有关,当电磁噪音的频率趋近于永磁同步电机的固有频率时,电机产生的电磁振动噪声会相应增强 [9] 。因此对电机的模态分析很有必要。
当一个单自由度系统收到外界简谐激振力的影响时﹐其运动方程如所示:
(1)
式中:m表示系统质量,c表示系统阻尼,k表示系统刚度,F表示简谐激振力的幅值,x表示振动位移。
式(1)是一个二阶微分方程,其特征值与固有频率相关,因此对系统进行模态分析后,就可以通过此方程来解得在此模态振型下的振动响应位移。
在此基础上,对于n个自由度的系统,则可以将式(1)表示为:
(2)
式中:
表示质量矩阵,
表示阻尼矩阵,
表示刚度矩阵,
表示振动激励的力矢量,
表示位移矢量,
表示速度矢量,
表示加速度矢量,均为n阶方阵。
求解此n阶方程每个模态下的位移响应,叠加可得整个系统的位移响应。
3.2. 定子铁芯模态分析
定子铁芯是永磁同步电机的重要结构,通常由0.35到0.5 mm厚的硅钢片叠压而成,材料参数如表2所示。

Table 2. Material properties of stator cores
表2. 定子铁芯的材料属性
若通过叠压的方式建立定子铁芯的模型,在后续网格划分步骤中,划分网格数大大增加,极大地降低了计算效率,同时硅钢片的叠压主要影响体现在轴向刚度上,而模态分析主要受径向刚度的影响,因此将模型简化为图2所示。

Figure 2. Schematic diagram of simplified stator core model
图2. 定子铁芯简化模型示意图
对定子铁心的前30阶自由模态进行有限元仿真分析,经分析得到了电机的自由模态振型。仿真结果显示,前六阶的固有频率均接近于零,主要原因在于定子铁芯在空间内具有的六个自由度,即在x、y、z三个方向上移动自由度和转动自由度。同时由于定子铁芯的结构特点与功能特性,在分析结果中,更关注轴向阶数为零的径向模态,从第七阶有效模态开始分析,得到了定子铁芯的2阶~5阶径向模态以及模态频率,结果如图3所示。
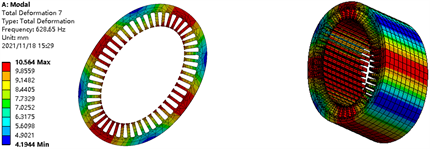
(a) 径向2阶模态629 HZ

(b) 径向3阶模态1684 HZ
 (c) 径向4阶模态2994 HZ
(c) 径向4阶模态2994 HZ (d) 径向5阶模态4279 HZ
(d) 径向5阶模态4279 HZ
Figure 3. Stator core radial modal analysis results
图3. 定子铁芯径向模态分析结果
由图3可知,定子铁芯的径向2阶模态频率为629 Hz,振动位移最大值为10.56 mm;定子铁芯的径向3阶模态频率为1684 Hz,振动位移最大值为12.86 mm;定子铁芯的径向4阶模态频率为2994 Hz,振动位移最大值为17.75 mm;定子铁芯的径向5阶模态频率为4279 Hz,振动位移最大值为25.08 mm。
3.3. 定子系统模态分析
在多数永磁同步电机中,定子铁芯都是与电机机壳装配的。在仿真中,设定定子铁芯与电机机壳的接触方式为绑定,同时对电机机壳进行简化处理,忽略模型中的圆角、倒角以及细小定位孔等对系统模态分析影响较小的微结构,网格划分结果如图4所示。

Figure 4. Schematic mesh delineation of permanent magnet synchronous motor casing
图4. 永磁同步电机机壳网格划分示意图
研究表明,机壳厚度对噪声振动有较大影响。因此本文在模态分析时,将电机机壳设定为不同的参数,并进行仿真分析定子铁芯和电机机壳装配后对固有频率的影响。在仿真中需要对装配体进行约束条件设置,为得到较为精确的仿真结果,约束条件应尽可能接近于工况。因此对装配体的底座螺纹孔添加固定约束。装配体的2阶~5阶径向模态仿真结果如表3和图5所示。

Table 3. Comparison of model frequencies for different thicknesses of chassis
表3. 不同厚度机壳模型频率对比
由表3可知,电机机壳厚度的增加可以显著提高径向模态频率,在2阶~5阶径向模态固有频率最大提升分别为9.24%、7.84%、8.28%、3.91%,而电机机壳厚度决定电机机壳刚度。因此,增大电机机壳厚度能够显著提高电机系统整体的固有频率。然而,选取过厚的电机机壳也会极大提升电机质量,一方面,极大的提高了其生产和运输成本,另一方面,不利于后续整车的可靠性设计以及维护。综合来看,选用13 mm的机壳厚度较为合适。如图5为本电机定子系统2阶~5阶模态振型。

 (a) 2阶 (b) 3阶
(a) 2阶 (b) 3阶
 (c) 4阶 (d) 5阶
(c) 4阶 (d) 5阶
Figure 5. Stator system modal analysis results
图5. 定子系统模态分析结果
由图可知,由于底座通过螺纹连接进行了固定约束,在各阶模态下均未变形。定子系统的2阶~3阶模态振型与定子铁芯相似,这是由于其类似的结构导致的。而高阶的模态振型与定子铁芯不一致,这可能是由于底座上的加强筋导致的。
3.4. 整机模态分析
在进行整机模态分析前,需要对整体模型进行简化处理。首先,该模型忽略了螺栓等细小结构对整体模态分析的影响,其次将轴承等复杂零件简化成圆环,并设置为面与面之间的接触,并略去倒角以及圆角的特征,这有利于网格划分以及缩短了分析时间。约束条件同定子系统,设定底座固定约束。永磁同步电机整机的网格划分结果如图6所示。

Figure 6. Stator system modal analysis results
图6. 定子系统模态分析结果
将整机径向的模态频率分析结果提取后与定子铁芯和定子系统的径向模态频率相比较,结果如图7所示。由图可知,选取较为合适的电机机壳厚度对于提升系统的模态频率有显著提升,而随着绕组、转子等部件的加入,使得电机的整机模态频率降低。
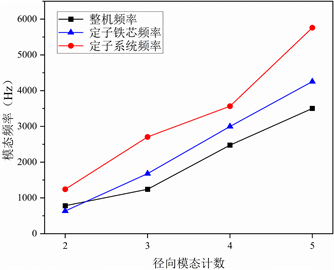
Figure 7. Comparison of radial modal results
图7. 径向模态结果对比
4. 振动相应分析
本节通过Ansys Workbench中的Harmonic response模块对永磁同步电机进行振动谐响应分析。王虹雨等人研究发现,永磁同步电机的振动主要是因为电磁场产生的电磁力波作用于定子齿上 [10] 。定子齿部同时受到电磁力以及转矩的作用,以一个定子齿为例,本文中采用的为电机工作在5850 rpm下的工况,对齿部施加转矩为252 Nm,施加电磁力密度为1 × 105 N/m2,转矩以及电磁力设置方式如图8所示,约束方式仍为电机底座固定约束。
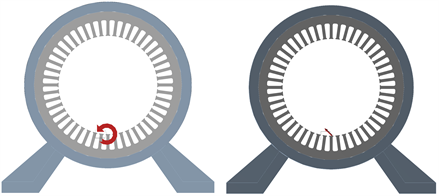
Figure 8. Schematic diagram of motor electromagnetic force and torque loading
图8. 电机电磁力和转矩加载示意图
在电机外壳选定一个参考面,通过Ansys分解分别得到观测面在负载下基于各频率的x轴和y轴振动加速度响应如图9所示,x轴和y轴振动变形幅值如图10所示。
 (a) x轴加速度
(a) x轴加速度 (b) y轴加速度
(b) y轴加速度
Figure 9. Schematic diagram of motor electromagnetic force and torque loading
图9. 电机侧壁负载振动加速度响应
由图9可知,在5850 rpm的工作情况下,x轴以及y轴的加速度的变化趋势基本一致,且x轴的加速度总体大于y轴的加速度。电机外壳上加速度峰值所对应的频率和其来源包括:转子中永久磁体产生的磁场谐波所引起的电磁力谐波频率、磁极的谐波磁场与定子的主磁场互相作用形成的谐波频率以及电磁力频率与电机固有频率相匹配的情况。
 (a) x轴位移
(a) x轴位移 (b) y轴位移
(b) y轴位移
Figure 10. Amplitude of load vibration deformation of motor sidewall
图10. 电机侧壁负载振动变形幅值
由图10可知,x轴以及y轴的变形幅值总体在一个较小的范围内波动。在x轴和y轴方向上振动位移较大的频率主要是由以下因素造成的:电机转子的旋转频率、由磁极引起的谐波频率以及磁极的谐波成分与定子的基波磁场交互作用而产生的谐波频率。
5. 结论
本文以某新能源汽车内的永磁同步电机为研究对象,通过三维建模建立了永磁同步电机的简化几何模型,并通过有限元仿真软件Ansys对定子铁芯、定子机壳系统以及电机整体进行了模态分析并按实际工况进行了振动分析。
首先对定子铁心的径向模态进行了仿真分析;其次研究了即可厚度对定子系统的影响,由仿真结果可知,电机机壳能够有效提升系统的固有频率,并与整机的固有频率进行了比较分析,结果表面:其他部件的加入会降低系统的固有频率。最后对永磁同步电机在负载下的振动响应情况进行了仿真并根据结果进行了分析,仿真结果表面:电机外壳上的振动主要来源于转子、磁极和定子由交互作用产生的电磁力谐波频率与电极固有频率对应而产生的共振。
因此,本研究为永磁同步电机未来的仿真分析以及优化设计提供了一定的参考依据。