1. 引言
资本资产定价理论源于1952年美国经济学家马克威茨(Markowitz)[1] 在《金融月刊》上发表的“Portfolio Selection: The Rand Corporation”一文，最早采用风险资产的期望收益率和用方差代表的风险来研究资产的选择和组合问题，被金融界视为现代资产组合理论的起点。
资本资产定价模型(the Capital Asset Pricing Model，CAPM)自被提出以来，便受到众多经济学者的青睐。早期的实证检验结果大都支持CAPM模型，自20世纪70年代以来，不少学者开始对其提出质疑，认为CAPM模型不可能得到实证检验。如何在中国市场上研究和运用CAPM模型，首先要解决该模型在中国股票市场能否成立的问题。
上海证券交易所自1990年12月诞生以来，经过22年的金融体制改革，截止到2012年年底，上市证券达998种，A股944只，B股54只。2012年年末A股股票市价总值达157912.65亿元，市场创新不断深化，市场信息披露制度不断完善，机构投资者队伍不断壮大。随着中国证券市场与国际市场的逐步接轨，投机者的生存空间被大大压缩，股票均衡价格不再以市场的意志为转移。在此背景下，对传统的CAPM模型在中国这一新兴的证券市场的适用性分析变得很有必要。
2. CAPM模型研究综述
美国学者William Sharpe[2] 、John Lintner[3] 和Jan Mossin[4] 分别于1964年、1965年和1966年独立地提出著名的CAPM模型，建立了一个以一般均衡框架中的理性预期为基础的投资者行为模型。
早期的实证研究进一步证实了CAPM模型的结论。Black，Jensen和Scholes (1972) [5] 以1926年1月至1966年3月在纽约证券交易所上市的公司月数据为研究样本，结果显示股票收益与系统性风险之间存在正向线性关系。在此基础上，Fama和MacBeth(1973) [6] 对美国1969年前的数据进行横截面两阶段回归检验，结果正如CAPM模型所预言的情况，平均股票收益与β系数之间的正相关关系成立。Clare, Pcicstly和Thomas(1998) [7] 用英国数据进行检验，证明无法拒绝β与英国股票市场截面平均收益正相关的假设。中国学者向方霓(2001) [8] 对沪市170只股票进行检验，认为沪市基本可以接受CAPM模型。李剑锋(2002) [9] 采用实证分析和经验验证手段，证明上海股票市场中股票的β值对收益具有一定的解释力，但对市场风险的度量缺乏显著性作用。许涤龙、张钰(2005) [10] 对上海股票市场37只股票进行实证研究，结果表明沪市股票收益率与β系数存在显著的正相关线性关系，但无风险收益率却为负值。
然而另有学者的研究成果则对CAPM模型提出质疑。Roll(1977) [11] 对CAPM模型提出著名的Roll批评，他认为由于无法证明市场指数组合的有效性，因而无法对CAPM模型进行检验。Reinganum(1981)[12] 研究发现：平均股票收益与β之间的正相关关系在美国70年代后的数据中消失了。Fama和French (1992) [13] 利用美国1962~1989年之间的数据证明即使在β为唯一解释变量的情况下，CAPM所预言的关系也不存在。Lewellen, Nagel(2006) [14] 对条件CAPM模型的实证分析效果提出了疑问，认为条件CAPM的估计结果受所选择的截面样本数据影响，因此对CAPM进行时间序列实证分析更有效。中国学者施东辉(1996) [15] 首次运用CAPM模型对50只沪市A股进行实证研究，得到沪市股票的系统性风险与预期收益间存在着显著的线性负相关关系，与CAPM模型所揭示的关系相反。杨朝军、邢靖(1998) [16] 对中国股票市场的价格行为进行了研究，结论表明我国股票市场风险和收益关系并不如CAPM理论所预期的那样，系统风险并非决定收益的惟一因素。陈小悦、孙爱军(2000) [17] 对中国股市研究发现：在控制股本规模以后，β系数对收益没有解释能力。阮涛、林少宫(2000) [18] 利用沪市40只股票对上海股票市场进行实证研究，结果表明：在仅包含β作为解释变量的横截面回归中，β系数显著为零。李璁，陈荣达(2010) [19] 选取上证交易所2003.1~2009.12期间的20只股票，通过BJS检验得出CAPM模型在中国股市严重不符。
综上，对CAPM模型在中国股票市场的适用性分析，相关研究结果并不统一。本研究尝试在市场组合、时间期限选择等问题上寻求突破，有助于实证研究结果更加充分合理，便于进一步澄清CAPM模型在中国市场的适用性问题。
3. 基于CAPM模型的实证检验
资本资产定价模型是在投资组合理论和资本市场理论基础上发展起来的，旨在研究证券市场中资产的预期收益率与风险资产之间的关系，以及均衡价格的形成。
无风险利率条件下的CAPM模型，其标准形式是：
(1)
其中
是第i种证券的收益率，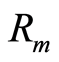
是市场证券组合的收益率，
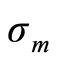是市场证券组合的标准差，
是第i种证券与市场收益率的协方差，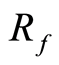
是无风险证券收益率。
定义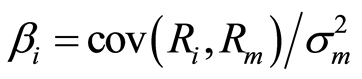
，则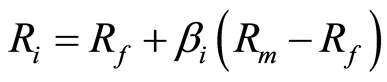
，这就是资本资产定价模型，即证券市场线。资本资产定价模型的关键在于
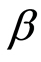系数的计算，
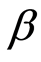系数是资本系统性风险的度量指标，反映资产价格对市场价格平均水平的敏感程度。
3.1. 样本选取
3.1.1. 样本数据的选择
本文以上海股票市场为研究对象，通过同花顺炒股软件筛选出2002年12月31日以前上市且处于正常交易的640只沪市A股，选择上证综合指数衡量市场风险。数据样本为2003~2012年历时10年经除权、除息处理后的月收益率数据，以月涨幅表示。
3.1.2. 无风险利率的确定
无风险利率指的是在没有风险和通货膨胀情况下的平均利率，是在本金没有违约、期望收入得到保证时的资本价值。本文选择三个月的居民定期存款年利率为无风险利率，其中2002~2012年三个月定期存款年利率调整情况如表1。
若某一月份的利率发生调整，以调整前后时间为权重，对该月的三个月定期存款年利率进行调整。如2007年3月18日调整后的三个月定期存款年利率为1.98%，调整前为1.80%，则2007年3月的三个月定期存款年利率为：(17/31) × 1.80% + (14/31) × 1.98% = 1.88%。考虑到与样本期间的相互匹配，再将
Table 1. The adjustment of three months deposit interest rate of residents from 2002 to 2012
表1. 2002~2012年三个月居民定期存款年利率调整
资料来源：中国银行官网金融资料整理汇总。
其调整到月收益率，即为无风险利率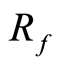
。
3.1.3. 收益率的计算
个股收益率
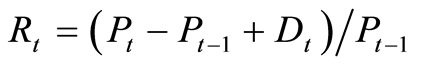(2)
其中：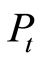
为该股本月末收盘价，
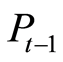为该股上月末收盘价，
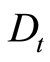为该股本月期间每股红利或利息收入。
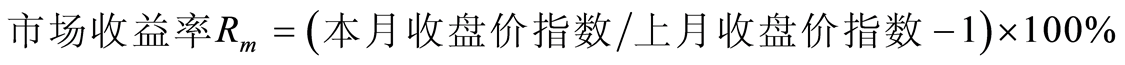(3)
3.2. 检验方法
3.2.1. 时间序列检验
(1) 组合的构造与组合收益率的计算
时间序列检验依据的是经典的BJS方法，本文与传统的BJS方法有所不同，主要是不再根据以往的
系数大小进行分组，而是依据以往针对中国股票市场的研究以及考虑到样本容量的大小[20] ，把所选取的640只沪市A股以等距离随机抽样的方式分成50组，记为Z01-Z50，每组13只股票，缺失的以0代替(见附录1)。
由于采用这种分组方法，与传统的检验方法相比，本文只把所选取的时间划分为两个时段：
第一期：2003.1.1~2008.12.31；第二期：2009.1.1~2012.12.31。
采用简单算术平均法求出50组股票组合2003~2012年120个月的月平均收益率，公式为：
(4)
其中：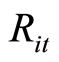
是第i个投资组合在t时刻的收益率；
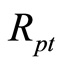是组合中第p只股票在t时刻的收益率；N是组合包含的股票数。
(2) 组合贝塔系数的估计
根据2003~2008年(第一期)各组月平均超额收益率和市场月平均超额收益率数据求得各组β系数，回归方程为：
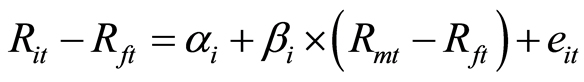(5)
其中：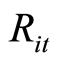
表示第i个组合在t时刻的预期收益率；
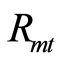表示上证综指在t时刻的预期收益率；
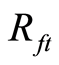表示t时刻的无风险利率；
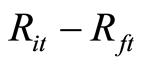为股票组合月平均超额收益率；
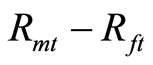为市场月平均超额收益率；
为估计残差；
、
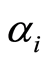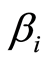为估计参数。
(3) 风险与收益关系的检验
将求出的组合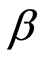
系数作为本阶段输入变量，结合2009~2012年(第二期)数据，检验组合风险与收益间的关系，公式为：
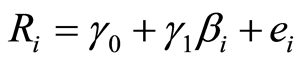(6)
其中：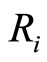
表示股票组合第二期月平均收益率；
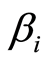表示股票组合第一期 
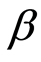系数；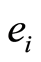 
为估计残差； 
、 
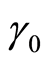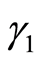为估计参数。
3.2.2. 横截面检验
采用标准的CAPM横截面检验方法(即Fama-Macbeth方法) ，在第二期数据截面上做回归，检验其有效性。公式为：
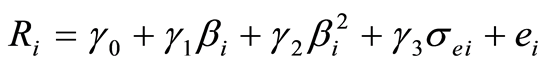(7)
其中：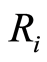 
表示股票组合第二期月平均收益率； 
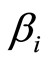表示股票组合第一期 
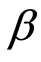系数；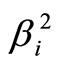 
表示第一期组合
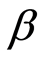系数的平方；
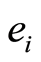表示估计残差；< img src=htmlimages\2-2350059x\cc5b80fb-74ea-4b44-9f47-f1d8498cc98d.png width=30 height=37.5 />、 
、 
、 
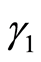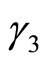表示估计参数。
4. 实证结果分析
4.1. 时间序列检验
依据时间序列检验过程，估计出2003~2008年(第一期)数据的组合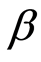 
系数，并对其进行描述性分析，结果如表2。
组合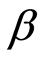
系数的R2处于0.424545~0.683468之间，拟合效果较好；
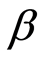系数的估计值最小为0.861096，最大为1.115083，均值为0.980494，绝大多数
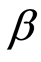系数的t、F检验值均显著。正态分布检验中JB = 0.407647，P = 0.815606，说明大多数
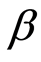估计值在均值附近，由此本文认为依据第一期数据估计的
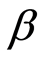系数是有效的。
随后，利用第二期(2009~2012)数据检验组合收益率与风险之间的关系。首先对收益率与贝塔值作散点图如图1，回归结果见表3。
利用第二期数据估计的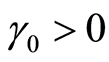
，则无风险利率为正，符合现实情况；
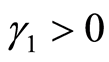表示沪市系统性风险与收益之间存在正相关关系，因此股票系统性风险在股票定价中有一定作用。但图1表明两者之间并不存在CAPM所预料的线性关系，0.9710的t值、0.9429的F值也说明这个线性关系并不明显。本阶段的检验明确表明组合收益率与
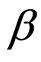系数表示的系统性风险之间不存在明显的线性关系，这与估计组合
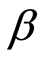系数得出的结论相矛盾。
4.2. 横截面检验
利用上述估计出的组合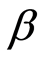
系数，采用传统的BJS方法在2009~2012年(第二期)数据上进行横截面检验，结果如表4。
本文利用第二期数据做了4次检验，回归结果不甚相同。2009年和2011年估计的参数为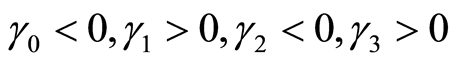
，2010年
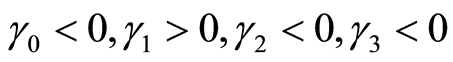，2012年
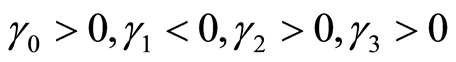。另外，
表示无风险利率为正，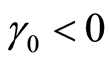
说明整个市场具有明显的投机特征；
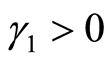说明证券组合的预期收益
Table 2. Descriptive analysis of beta coefficient
表2. Beta系数描述性分析
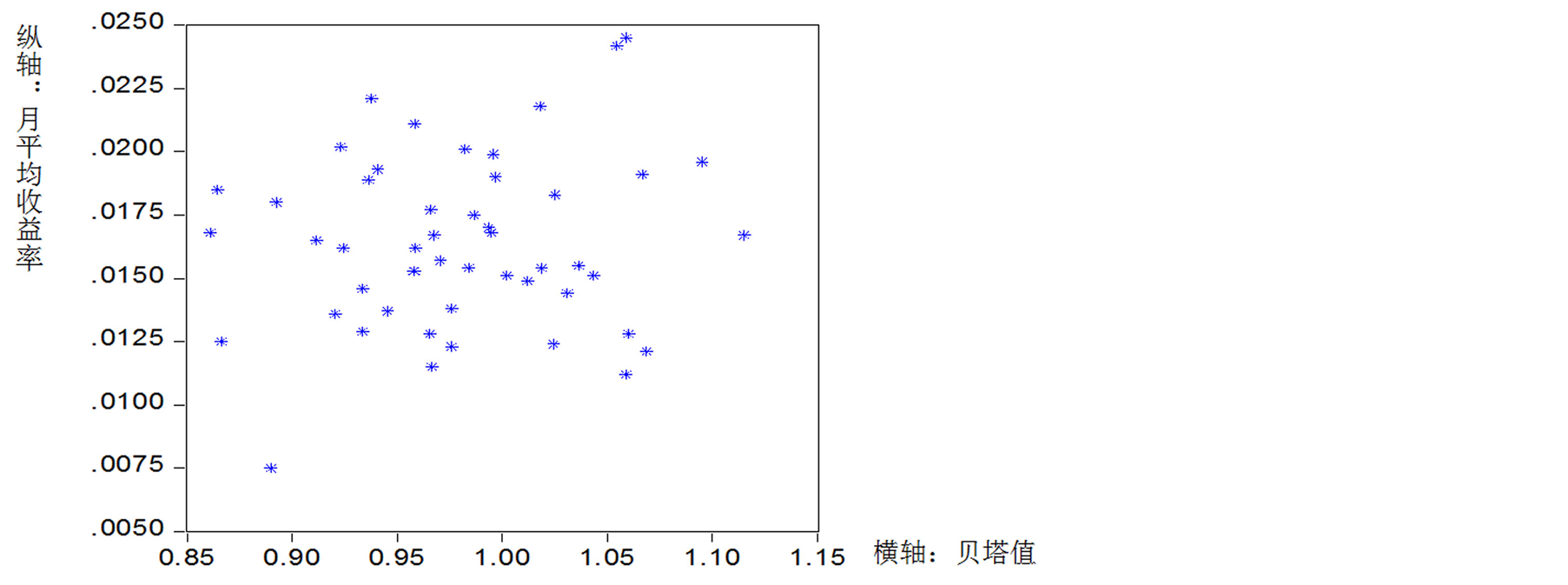
Figure 1. Scatter of average monthly yield and beta value from 2009 to 2012
图1. 2009~2012年月平均收益率与贝塔值散点图
Table 3. The test of the relationship between income and risk
表3. 收益与风险关系的检验
率与系统性风险存在如CAPM所预期的正相关关系，反之不存在；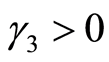
说明非系统风险在证券定价中有一定作用。上述四个方程结果不同，但共同点是t值、F值、R2都不高，说明还有其他风险因素在股票定价中有不可忽视的作用。
4.3. 沪市投资风险构成分析
股市风险分为系统风险和非系统风险，系统风险是整个股市所面临的风险，无法通过多样化投资加以消除，能够通过投资组合降低的风险只有非系统性风险。对股市风险的度量，本文结合50组数据，采
Table 4. The results of cross-sectional test
表4. 横截面检验结果
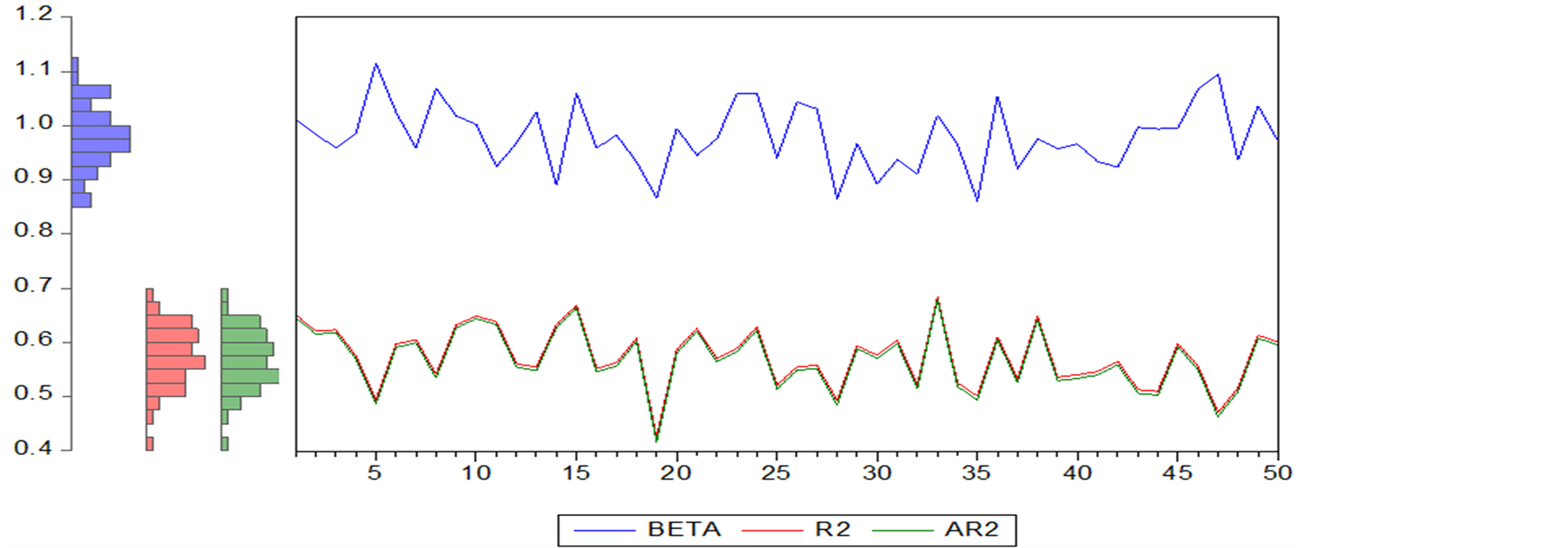
Figure 2. 50 groups’s beta coefficient and coefficient of determination
图2. 50组β系数和可决系数
Table 5
用两个指标：β系数、R2。
虽然通过上述实证检验本文否定了CAPM在上海股票市场的有效性，但由于方差是风险的近似测量，CAPM对股票收益风险的分类仍是成立的。收益率的方差用公式(8)[21] 表示：
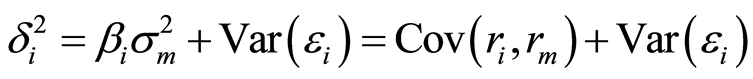(8)
其中系统风险在总风险中的比例可用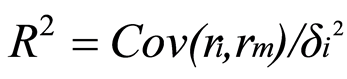
表示，如图2，横轴表示组号，纵轴分别表示β、
、
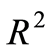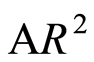(调整后可决系数)的值。
结合表2和图2可知，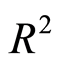
的变化范围为0.424545~0.683468，均值为0.573536，与国外成熟的股票市场的风险比例(90%以上)相比，仍属较低。β值的变化范围为0.861096~1.115083，均值为0.980494，组合β值趋于稳定。这说明：由若干只股票构成的证券组合，其β值的稳定性有一定程度的提高。从中可以看出我国的证券市场经过二十多年的发展正逐步走向成熟，选择合适的股票组合进行投资有利于分散绝大部分非系统风险。
5. 结语
本文以上海股票市场为研究对象，通过对处于正常交易的640只沪市A股进行时间序列检验以及横截面检验，得出如下结论：
①在我国市场上进行CAPM实证检验，结论与数据样本的选择有很大的联系，不同的样本会得出不同的结论，一定程度上说明沪市还是一个不成熟的市场，价格波动较大。②时间序列检验和横截面检验表明沪市不符合CAPM模型，但通过β系数的渐趋稳定性看出CAPM在中国股市的适用性在增强。③上海股市的股票定价不仅受系统风险的影响，而且受非系统风险的影响。
分析资本资产定价模型在我国上海股票市场不适用的原因，主要有以下几点：
①CAPM模型本身有较多严格的假设，在现实的股票市场上基本上难以满足；②检验过程中由于选取样本、期间、市场收益率等原因使得检验结果存在误差；③中国证券市场存在缺陷，如中国证券市场对政府行为极其敏感，股市投资者结构不合理等；④中国证券信息披露制度不健全。⑤与中国资本市场的发展、中国自身经济建设和周边环境发展有关。
为进一步促进中国证券市场持续、健康发展，本文提出如下建议：①审慎地制定政府政策，减弱股市对政府行为的敏感性；②大力培育机构投资者，促进投资主体机构化；③消除信息不对称，完善信息披露制度。
附录(Appendix)
Appendix 1. Sample packet list
附录1. 抽样分组列表
续表