一种动态规划算法模型预测控制在混合动力汽车控制策略中的应用

Application of a Dynamic Programming Algorithm Model Predictive Control in Hybrid Electric Vehicle Control Strategy

摘要: 良好的混合动力汽车控制策略，不仅能满足车辆的动力需求，而且能有效地节省燃油、减少排放。本研究提出了模型预测控制在混合动力汽车的构建，针对基于动态规划算法在模型预测控制的应用论述了求解过程以及参考轨迹的使用。在某一特定工况下，对混合动力汽车进行了仿真，结果表明该控制方法在合理分配发动机和电动机的转矩时，可以有效降低燃油消耗的目的，进而验证了该控制策略的有效性。

Abstract: Good control strategy of hybrid electric vehicles can not only meet the power demand of vehicles, but also effectively save fuel and reduce emissions. In this paper, the construction of model pre-dictive control (MPC) in hybrid electric vehicle (HEV) is proposed. The solving process and the use of reference trajectory are discussed for the application of MPC based on dynamic programming algorithm. The simulation results show that the control method can effectively reduce fuel con-sumption when the torque of engine and motor is reasonably distributed, and the effectiveness of the control strategy is verified.

1. 绪论

安全、节能和环保是当今汽车工业重要的发展方向和热点研究领域。随着汽车生产量和保有量的激增，对交通、资源和环境造成了巨大压力。近年来，迫于资源和环境的压力，电动汽车成为全球汽车工业发展的热点。混合动力汽车的控制策略即将发动机的动力输出和电机的动力输出以一种最为合理的方式匹配到一块，要求在保证汽车动力需求的基础之上，尽量减少汽车的尾气排放和减小燃油消耗。

文献 [1]为保证车辆在坡度变化时能保持恒速下坡，根据给出的制动系统数学模型，采用自适应模型预测控制方法设计控制系统。文献 [2]针对汽车系统的非线性和强耦合特性，探索了再生制动中能够有效保证车辆稳定性、提高控制精度和再生制动能量回收率的改进的非线性模型预测控制方法。文献 [3]阐述了随机模型预测控制(SMPC)在先进混合动力系统车辆动力管理中的应用。文献 [4]介绍了一种具有最优性和可扩展性的低复杂度电动汽车充电调度的模型预测控制方法。文献 [5]基于模型预测控制的混合动力客车再生制动能量回收控制策略，在保证制动能量回收最大化的同时，保证了制动稳定性。本研究将提出一种动态规划算法模型预测控制在混合动力汽车控制策略，通过对模型预测控制在混合动力汽车控制策略的构建，将动态规划算法应用到模型预测控制上，对基于动态规划算法的模型预测控制和SOC参考轨迹的使用进行分析和研究。本研究通过利用动力电池SOC参考轨迹作为基于动态规划模型预测控制的状态参数约束条件，进行实时控制，同时对发动机和电动机的转矩进行优化处理，可以在很大程度上降低混合动力汽车的消耗，以实现节约能源和节能减排。

2. 基于模型预测控制的混合动力汽车优化控制函数的设计

为了保证混合动力汽车工况行驶时，合理分配发动机和电机的转矩，以保证整车动力输出的正常工作，通过提出模型预测控制策略来进行动力系统的控制，进而可以降低整车的能耗和节约能源，提高车辆的行驶里程。

本研究通过提出的基于模型预测控制的混合动力汽车控制策略进行整车优化控制。通过获取车辆行驶的前一时刻的运行速度和加速度等信息，结合当前时刻的运行速度和加速度，构建车辆运行状态的预测模型，进行车辆运行状态的预测，进而为预测时域内控制提供最优化信息。根据所计算预测的车辆未来时域内的车辆状态，进而计算车辆的需求转矩，采用特定的算法，在一定的约束条件下获取在预测时域内系统的电机转矩最优序列。将预测控制模型计算所得的最优电机转矩序列的第一个值附加给车辆，然后进入下一时刻，继续获取车辆历史速度、加速度等信息，预测下一时段的车辆运行状态，以修正上一时刻的预测值。最后，重复预测、优化、校正的步骤。

在进行动态规划的混合动力汽车控制策略构建时，其优化指标函数为：

$J_k={\displaystyle \underset{k}{\overset{k+p}{\sum }}L\left(x\left(t\right),u\left(t\right)\right)}={\displaystyle \underset{k}{\overset{k+p}{\sum }}f\left(t\right)}$ (1)

式中， $x\left(t\right)$ 表示 $t$ 时刻蓄电池的SOC值的状态变量； $u\left(t\right)$ 表示 $t$ 时刻的电机转矩变量； $L$ 表示某一时刻的指标函数； $J_k$ 表示总的指标函数； $p~p+k$ 表示预测时域。 $f\left(t\right)$ 表示车辆在 $t$ 时刻的瞬时燃油消耗量。

3. 基于动态规划在混合电动汽车模型预测控制的应用

通过使用研究的模型预测控制方法进行车辆未来时刻运行状态的预测，再结合动态规划算法，可以得到基于工况状态下电机转矩的最优序列，进而可以求解混合车辆行驶过程中的多阶段决策问题。当进行某一时域预测时，转态变量需要在一定的约束条件下进行优化控制，然后利用动态规划算法中设计的SOC变化规律，从而可以得到SOC的参考轨迹作为优化过程中的SOC约束条件。

3.1. 动态规划在模型预测控制的求解

假设在模型预测控制系统的 $k$ 时刻，其系统的预测时域为： $k~k+p$ 。如果在该区间内通过基于动态规划算法的模型预测控制系统求解最佳电机转矩序列以及离散状态变量可以通过逆序求解每个时刻下的电机转矩最优值和最优指标值。

在设计的预测时域内，可以得到最优指标函数为：

$J_k^{\ast }\left(SOC\left(k\right)\right)=\underset{u\left(k\right)}{\min }\left[L\left(SOC\left(k\right),u\left(k\right)\right)+J_{k+1}^{\ast }\left(SOC\left(k+1\right)\right)\right]$ (2)

式中， $J_k^{\ast }\left(SOC\left(k\right)\right)$ 表示由 $k$ 时刻到 $k+p$ 时刻的最优指标值； $u\left(k\right)$ 为预测时域内 $k$ 时刻对应的最优转矩值。只取预测时域内的最佳电机转矩序列的第一个值，不取剩下时刻的电机转矩序列，以减少计算量，提高运行速度。

3.2. SOC参考轨迹及使用

在循环工况确定的情况下(如图1所示)，经过全局优化得到的SOC变化曲线具有一定的规律性，随着汽车行驶里程的增加，SOC的变化为从初始SOC值缓慢下降直至SOC的最低门限值，如图1所示，SOC下降平稳且围绕直线平稳波动。由于全局优化控制策略为混合动力汽车控制策略中最理想的控制方

Figure 1. Power demand diagram under cyclic condition

图1. 循环工况下的需求功率图

法，因此全局优化得到的SOC变化曲线可作为模型预测控制中SOC变化的约束条件，但是，由于全局优化必须提前获取整个循环工况的车车辆运行状态等信息，无法应用到实时控制中。因此，本文结合动态规划得到的SOC变化规律提出理论SOC变化曲线的使用。

假定汽车到达目的地的行驶时间确定，根据动态规划的SOC变化规律，SOC的变化基本上线性衰减，将SOC的理论变化轨迹定义为从车辆运行起点SOC的最高值线性减少到SOC的最低值，将理论SOC变化轨迹作为SOC参考轨迹，对模型预测控制进行约束，SOC理论参考轨迹如图1所示。

对于任意时刻 $k$ 的参考SOC值可由以下公式计算可得：

$SO{C}_r\left(k\right)=SO{C}_0-\frac{k}{s}\left(SO{C}_0-SO{C}_f\right)$ (3)

式(3)中， $SO{C}_r\left(k\right)$ 表示参考轨迹下k时刻的SOC值； $SO{C}_0$ 表示车辆运行初始状态的SOC值，可根据实际情况自行设定； $SO{C}_f$ 表示SOC的最低门限值； $s$ 表示形式总里程的时长。

获取SOC参考轨迹的主要作用在于限制实际运行下SOC在参考SOC轨迹下的波动，每一时刻SOC的参考值通过公式(3)计算可得，初始SOC值和终止SOC值可根据实际情况自行定义。通常情况下，初始SOC值应预留出一部分电量为车辆启动提供能量，因此应将初始SOC值下移一个微小量：

$SO{C}_0=SO{C}_i-0.01$ (4)

式中， $SO{C}_i$ 表示出发时刻的SOC值。

在车辆运行的每一时刻 $k$ ，预测时域为 $k~k+p$ ，一般情况需对每个时刻SOC值进行约束以提高模型控制的精度，通常采用二次代价函数的方式进行约束，公式如下：

$J_k={\displaystyle \underset{k}{\overset{k+p}{\sum }}\left(f\left(t\right)+h\left(SOC\left(t+\text{1}\right)\right)\right)}$ (5)

式(4)中，h为SOC的代价函数，具体表达公式如下：

$h\left(SOC\left(t\right)\right)=\{\begin{array}{l}0,SOC\left(t\right)\ge SO{C}_r\left(t\right)\\ \alpha {\left(SOC\left(t\right)-SO{C}_r\left(t\right)\right)}^2,SOC\left(t\right)<SO{C}_r\left(t\right)\end{array}$ (6)

式(6)中， $SO{C}_r\left(t\right)$ 表示 $t$ 时刻的SOC参考值； $\alpha$ 表示权重系数，取 $1\times {10}^{10}$ ； $SOC\left(t\right)$ 表示实际SOC值。当实际SOC值大于等于参考SOC值时，代价函数为0，对于指标函数不起任何作用，当实际SOC值小于参考SOC值，代价函数值比较大，且实际SOC值与参考SOC值差值越大，代价函数值越大。这样可以使SOC的实际运行轨迹始终保持在参考轨迹的上方，起到对SOC约束的作用。

本文以某款混合动力汽车为原型，以MATLAB仿真软件为基础进行了仿真实验。整车质量1070 kg，动力电池额定电压72 V，电池容量150 AH，电机功率额定功率5.5 kW，额定转速3000 rpm。UDDS工况是由美国环境保护署EPA制订的，用来测试车辆城市道路下各种性能的循环工况。在循环工况下的需求功率的情况下，对系统进行仿真，结果如图2所示。

从图2可以看出使用本文设计的基于动态规划的模型预测控制可以较好地进行系统的优化，SOC值与理想结果很接近，达到了预期的效果。

4. 结论

本研究针对混合动力汽车控制策略在模型预测控制上的应用作了论述，提出动态规划算法在模型预测控制中的应用，主要用于预测时域内的最优控制电机转矩序列的求取和动态规划得到的参考SOC轨迹

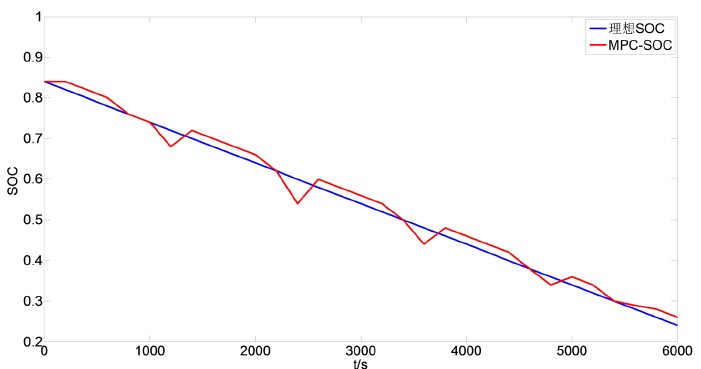
Figure 2. SOC curve of storage battery

图2. 蓄电池的SOC变化曲线

的使用，同时介绍了模型预测控制的求解步骤和SOC参考轨迹对实际每一时刻SOC值的约束。从而证明了模型预测控制以不同预测模型为基础，采用滚动优化的原则，在线性和非线性的控制系统中具有鲁棒性强、效果良好以及稳定性高的优点得到了广泛的应用。

基金项目

河南省科技攻关项目(172102210124)；河南省高等学校青年骨干教师培养计划项目(2016GGJS-287)；河南省高校重点科研项目(18B460003)。