一种三维光子晶体温度特性研究

Temperature Characteristics of Three-Dimensional Photo Crystal

摘要: 本文采用平面波展开法研究了三维光子晶体的带隙与环境温度变化之间的关系。环境温度变化会使三维光子晶体介质的折射率发生变化，三维光子晶体介质折射率的变化会引起三维光子晶体的带隙发生变化。本文研究温度对三维光子晶体带隙的影响，可为三维光子晶体温度测量器件的制作提供理论基础。

Abstract: In this paper, the relationship between the energy band of three-dimensional photonic crystal and the change of ambient temperature are studied by use of the plane wave expansion method. The change of the environment temperature will change the refractive index of the three-dimensional photonic crystal medium, and the change of the refractive index of the three-dimensional photonic crystal medium will change the energy band of the three-dimensional photonic crystal. This paper studies the influence of temperature on the band gap of three-dimensional photonic crystal, which can provide theoretical basis for the fabrication of three-dimensional photonic crystal temperature measuring devices.

1. 引言

温度是科学与技术中最基本的物理量之一，也是工农业生产及工程技术中最普遍的重要参数之一。随着科技的快速发展，人们对平时的生活环境以及生产过程的要求越来越高，尤其是生产过程，因此，对新型的温度测量手段的研究具有重要意义。

光子器件的出现在技术发展中提供了解决方向与途径。在1987年Yablonovich [1] 和S. John [2] 提出光子晶体，它是由多种折射率的介质按照周期性排列而成的人工微结构。光子晶体最主要的特征就是具有光子带隙结构，在某一些频率范围之内的光是不能透过去的，而另一些频率范围内的光是可以透过去的，就是因为它具备这种特征，它在很多的地方都有着应用的价值，可以加工成有价值的器件 [3]。 影响着光子带隙的主要原因有两个：第一个是光子晶体的结构，最基本的三维光子晶体结构有三种，钻石结构，木堆结构和面心立方结构 [4]；第二个是介电常数的大小。本文以三维光子晶体的折射率作为研究点，分析介质折射率与环境温度的关系，从而去分析三维光子晶体与温度的关系，验证其作为光子温度测量器的可行性。

2. 理论模型

三维光子晶体相对于一维，二维光子晶体，它独特的地方是它在三个方向上都有着周期性结构，所以它可以容易的构成各个方位的光子带隙，因此可以有效控制着光的传播，所以说三维光子的结构会更为复杂 [5] ，但是它的理论计算相会简单一点。本文选用钻石结构光子晶体作为研究对象，晶体结构图如图1 [6] 所示。

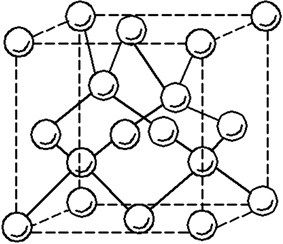
Figure 1. Schematic diagram of diamond crystal structure

图1. 钻石晶体结构示意图

本文选用高介电材料Si作为背景材料，用空气小球来构成的钻石结构的三维光子晶体。我们假设这种结构是在介电材料Si中钻孔来形成的 [7]。 取晶格常数a = 1，介质球半径r = 0.31，空气折射率n = 1，介电常数为1。Si的折射率n₁ = 3.3。背景介质材料Si的折射率与温度关系如图2所示。

Figure 2. Relationship between temperature and refractive index of Si

图2. 介质硅折射率与温度的关系

由图可知，Si的折射率随着温度的增而增大，折射率和温度成比例关系。环境的温度变化可以由材料的折射率来体现。折射率和材料Si介电常数的数量关系如式(1)所示：

$n^2=\epsilon$ (1)

根据公式(1)我们可以知道，环境的温度变化是可以通过三维光子晶体的介电材料的介电常数来反应的。

现在我们知道的计算三维光子晶体的方法有这几种：传输矩阵法、时域有限差分法、平面波展开法等等 [8]。 对比前两种方法，平面波展开法是更加简单方便的，是我们计算光子晶体很常用的一种方法。平面波展开法建立在麦克斯韦方程的基础上。本文采用的麦克斯韦方程 [9] 如下所示：

$\frac{1}{\stackrel{d}{X}\left(r\right)}\nabla \times \left[\nabla \times \stackrel{d}{E}\left(r,t\right)\right]=-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}E\left(r,t\right)$ (2)

$\nabla \times \left[\frac{1}{\stackrel{d}{X}\left(r\right)}\nabla \times \stackrel{d}{H}\left(r,t\right)\right]=-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}\stackrel{d}{H}\left(r,t\right)$ (3)

式中，X(r)是一种线性的，各项周期性的函数和同性的函数，假如光子晶体是一种非磁性的介质，那么磁导率(r) = 1，假如方程有波动形式的解，则方程可以写成：

${\theta }_E\stackrel{d}{E}\left(r,t\right)=\frac{1}{\stackrel{d}{X}\left(r\right)}\nabla \times \left[\nabla \times \stackrel{d}{E}\left(r\right)\right]=\frac{k^2}{c^2}\stackrel{d}{E}\left(r\right)$ (4)

${\theta }_H\stackrel{d}{H}\left(r,t\right)=\frac{1}{\stackrel{d}{X}\left(r,t\right)}\nabla \times \left[\nabla \times \stackrel{d}{H}\left(r,t\right)\right]=\frac{k^2}{c^2}\stackrel{d}{H}\left(r\right)$ (5)

通过傅里叶变换，得到公式如下：

$\frac{1}{\stackrel{d}{X}\left(r\right)}={\sum }_G\frac{1}{\stackrel{d}{X}\left(r\right)}\left(G\right){\text{e}}^{iG°r},\stackrel{d}{H}\left(r\right)=\underset{k,\lambda }{\sum }\hat{e}\left(k,\lambda \right)h\left(k,\lambda \right){\text{e}}^{ik°r}$ (6)

根据布里赫定理得到：

$\stackrel{d}{E}\left(x,t\right)=\exp \left[i\left(k°x-kt\right)\right]\underset{G}{\sum }\stackrel{d}{E}\left(G\right)\exp \left[iG°x\right]$ (7)

$\stackrel{d}{H}\left(x,t\right)=\exp \left[i\left(k°x-kt\right)\right]\underset{G}{\sum }\stackrel{d}{H}\left(G\right)\exp \left[iG°x\right]$ (8)

将公式(6)，(7)，(8)带入到(2)，(3)得到以下方程式：

$\left(\stackrel{d}{K}+\stackrel{d}{G}\right)\times \left[\left(\stackrel{d}{K}+\stackrel{d}{G}\right)\times \stackrel{d}{E_G}\right]+\frac{K^2}{G^2}\sum \stackrel{d}{E_G}=0$ (9)

$\left(\stackrel{d}{K}+\stackrel{d}{G}\right)\times \left[{\displaystyle \underset{G}{\sum }\frac{1}{X\left(r\right)}}\left(\stackrel{d}{K}+\stackrel{d}{G}\right)\times \stackrel{d}{H_G}\right]+\frac{K^2}{C^2}\stackrel{d}{H_G}=0$ (10)

公式(9)、(10)是三维光子晶体中光传播的本征方程式，K和k通过解方程式(9)，(10)就可以得出K和k的关系，就可以算出三维光子的带隙结构。

3. 数据分析

本文用MALTAB软件来模拟，分析三维光子晶体的带隙结构。从而分析三维光子晶体的带隙结构和环境温度变化之间的关系。

选用晶格常数a = 1，空气介电常数 = 1，介质球半径r = 0.31的情况下，温度为0℃和80℃时的三维光子晶体的带隙结构分别如图3和图4所示。横坐标是波矢量，单位是rad/m，纵坐标是归一化频率。可以用归一化转换式计算波长：

$\frac{a\cdot 2\cdot \pi }{w}=\frac{\lambda }{a}$ (11)

公式中：a——晶格常数；

w——角频率；

$\lambda$ ——波长。

Figure 3. Energy band structure at 0˚C

图3. 温度为0℃时带隙结构图

Figure 4. Energy band structure at 80˚C

图4. 温度为80℃时带隙结构图

通过公式(11)求出三维光子晶体的起始波长，终止波长和禁带宽度，并分析环境温度与其关系 [10]。 我们通过MATLAB软件进行仿真，得出三维光子晶体带隙结构禁带的起始波长，终止波长和禁带宽度，并分别分析它们与环境温度之间关系。三维光子晶体的终止波长与环境温度变化之间的关系如图5所示。由图5可知，三维光子晶体带隙结构禁带的终止波长随着环境温度的升高而升高，三维光子晶体带隙结构禁带的终止波长变化与环境温度的变化呈线性关系。表明随着温度升高，背景介质材料的介电常数增大，随之禁带终止波长也增大了。经过研究分析得出，在温度由0℃变化到80℃时，光子带隙结构的禁带终止波长从2077.15 nm增加到2117.75 nm。禁带终止波长和环境温度呈线性关系，其关系如下式：

${\lambda }_2=0.5075t+2077.15$ (12)

式中， ${\lambda }_2$ 为终止波长，单位为nm；t为环境温度，单位为℃。

Figure 5. Relationship between termination wavelength and temperature

图5. 终止波长与温度关系

测量晶体的灵敏度，可以通过测量光子禁带的起始波长 [11]。 三维光子晶体禁带的起始波长与环境温度变化之间的关系如图6所示。由图6可知，三维光子晶体带隙结构禁带的起始波长随着环境温度的升高而升高，三维光子晶体带隙结构禁带的起始波长变化与环境温度的变化呈线性关系。表明随着环境温度升高，背景介质材料的介电常数增大，随之禁带起始波长也增大了。经过研究分析得出，环境温度从0℃增加到80℃时，起始波长从3064.45 nm增加到3148.25 nm。禁带起始波长和环境温度呈线性关系，其关系如下式：

${\lambda }_1=1.0475t+3064.45$ (13)

式中， ${\lambda }_1$ 为起始波长，单位为nm；t为环境温度，单位为℃。

Figure 6. Relationship between start wavelength and temperature

图6. 起始波长与温度关系

三维光子晶体带隙结构的禁带宽度与环境温度变化之间的关系如图7所示。由图7可知，三维光子晶体带隙结构的禁带宽度随着环境温度的升高而升高，三维光子晶体带隙结构的禁带宽度的变化与环境温度的变化呈线性关系。表明随着环境温度升高，背景介质材料的介电常数增大，随之禁带宽度也增大了。经过研究分析得出，温度从0℃增加到80℃时，禁带宽度从987.3 nm增加到1020.5 nm。光子带隙的宽度越宽时，光子晶体的温度敏感性能越好。禁带宽度和和环境温度呈线性关系，其关系如下式：

${\lambda }_0=0.415t+1020.5$ (14)

式中， ${\lambda }_0$ 为起始波长，单位为nm；t为环境温度，单位为℃。

Figure 7. Relationship between band gap and temperature

图7. 禁带宽度与温度关系图

4. 结论

本文对三维光子晶体的带隙结构与温度变化之间的关系进行了研究，随着环境温度的变化，三维光子晶体的禁带起始波长、终止波长和禁带宽度都随温度的变化而变化。研究结果表明，三维光子晶体的禁带起始波长、终止波长和禁带宽度与温度都呈线性关系。

基金项目

浙江省科技创新活动计划资助项目(2018R428006)。

NOTES

^*通讯作者。