应急救援中智能无人机路径规划

Intelligent UAV Path Planning in Emergency Rescue

摘要: 为了能使无人机在真实环境中实现更安全有效地安全避障，本文提出了基于改进的自适应遗传算法的无人机避障路径规划模型，利用matlab模拟出障碍物的三维模型后和所处的空间范围，应用遗传算法让无人机在三维环境中完成安全有效的路径规划，通过在不同形状的障碍物下进行仿真，仿真结果表明，改进后的避障路径规划模型能够快速找到一条更短更安全的路径，达到了在应急情况中无人机能够快速实施救援的目的。

Abstract: This paper is proposed to make the unmanned aerial vehicle (UAV) in a real environment safe obstacle avoidance more safely and effectively, based on the improved adaptive genetic algorithm of unmanned aerial vehicle (UAV) obstacle avoidance path planning model, using the matlab simulate the 3D model of the obstacles and scope of space, after using a genetic algorithm for unmanned aerial vehicle (UAV) completed in the 3D environment is safe and effective path planning, Through the simulation under different shapes of obstacles, the simulation results show that the improved obstacle avoidance path planning model can quickly find a shorter and safer path, and achieve the purpose that the UAV can quickly implement rescue in emergency situations.

1. 引言

随着现代科技的不断进步，无人机技术在灾难救援方面得到了广泛的应用，而自然灾害往往具有突发性、瞬时性、不确定性，仅靠传统的人工救援方式是不能有效且安全地解决救援问题，由于卫星遥感与航空遥感在获取灾情时受到时空分辨力、外界环境以及使用成本等因素的影响 [1]，其在灾难救援方面的应用受到一定限制。无人机应急救援相比于其他救援类型，其优点在于自身体积小，有较强的飞行能力，并且它操作性简单，覆盖面广泛，实时性强，效率高，可以穿梭于很多复杂且危险的地形进行勘察和定位，这让救援人员对灾难情况有了更加透彻清晰的了解。

为了能让无人机在三维环境中搜索最优路线，于涛 [2] 针对民用无人机的飞行航迹特点，利用蚁群算法，虽然最终实验结果较为满意，但算法较为复杂，存储空间较大；祁永强 [3] 基于改进的人工水流算法，设计了根据环境进行选择的启发因子，使无人机自主逃离陷阱区。郭一聪 [4] 提出了针对传统的人工势场法的3个缺陷，分别进行了算法改进，解决提高了飞行安全性；吴亚雷 [5] 将A*算法与生物神经动力学模型融合优化，提高了A*算法的全局搜索能力并实现了动态避障能力。本文提出利用遗传算法来解决路径规划问题，将求解问题的各种解作为一个个体，将这些个体按一定几率选择、交叉、变异，进化成下一代，并逐步淘汰适应度值低的解，增加适应度值高的解，从而达到高质量的优化以及产生解决问题的方案 [6]，针对不同障碍物的形状，对其进行数学建模，使得无人机能够在三维空间中能安全有效的到达救援区域。

2. 地图预处理

本文将地形划分为一系列的栅格，在数学视角下是由边联结起来的结点的集合，一个基于图块拼接的地图可以看成是一个栅格图，栅格图之间各连线交点即是一个节点。当建立起栅格地图后，便利用遗传算法对地形模型进行收敛性实验，得出不同的遗传代数对其的影响，并发现具有自适应性能的遗传算法模型具有更好的收敛性与计算能力，可以更好地运用于路径规划 [7]。

首先要做到的就是数字地图的预处理。为了便于计算，本文将障碍物模拟成圆柱体或长方体，利用Matlab进行数据输入和处理，得到一个三维真实模拟环境，设置起点和终点，仿真的基本设置参数如下，整体的地图空间范围为27 km × 30 km × 1800 m，并将坐标轴进行等间距设置，其中路径起点坐标为[1.4 2.4 0.95]，坐标为[24.2 29.4 4.6]，得到如图1所示的三维模型图。

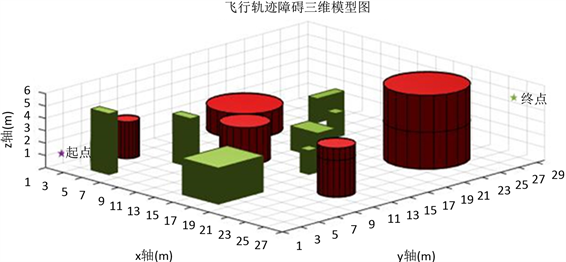
Figure 1. Three-dimensional model diagram of flight trajectory obstacle

图1. 飞行轨迹障碍三维模型图

3. 算法设计流程

在程序运行后无人机会先进行定位在地图上的位置，然后规划出大致路线并开始行动。之后在行动中再利用超声波传感器来检测障碍物的存在，并判断挡住当前飞行路线的障碍物高度。当飞行高度小于等于障碍物高度时，传感器会收集障碍物的数据 [8]，在得到障碍物的高度和水平距离数据后，无人机能够获取障碍物的图象，并由此精确感知障碍物的具体轮廓 [9]，而当飞行高度大于障碍物高度时，无人机就将直接按照之前的计划路线进行持续飞行 [10]，并在飞行过程中持续对路线上的障碍物高度进行检测。

之后无人机就能够对飞行区域建立地图模型然后利用公式开始规划合理线路。首先是利用数学公式计算得到安全节点的集合，之后再计算所有安全节点间的距离，这时需要进行一个简单的距离判断。当完成对所有的安全节点之间距离的判断后，选择其中能形成一条完整路径的最短距离安全节点，计算结束之后，将所有短距离计算的结果进行相加，求出所有短距离的总和，得到最短路径 [11]，具体流程见图2。

Figure 2. Design flow chart

图2. 设计流程图

4. 满足无人机安全飞行公式建模

遗传算法作为一种多点搜索算法，能够在大型区域内进行广泛而有效的搜索，所以为了减缓程序在仿真过程中的负担，减少算法在空间中的所占内存，并基于简洁、高效、可读性高、适用性好等原则，故采用一些数学公式进行建模和计算。由于有了传感器以及高度测试器等设备的帮助，无人机的飞行高度便可以得知，则先表示出无人机路径计算的最基本的公式：

$d\left(i,j\right)=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2+{\left(z_i-z_j\right)}^2}$ (1)

$D={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}\min \left(d\left(i,j\right)\right)}}+l_{偏航}$ (2)

$\left(x_i,y_i,z_i\right)$ 、 $\left(x_j,y_j,z_j\right)$ ——任意两安全节点的坐标

D——总路径长度

为了有效地观察所规划地区的障碍，以及更加精确地标示出障碍的地理位置，方便实现无人机的避障功能，针对无人机飞行高度小于障碍物高度的情况，本文先将无人机运行假设进一个二维的平面状态，所规划地区的地图划分成正方格的栅格图。由于需要测试无人机的避障功能，所以需要根据障碍物与节点具体位置来分情况讨论，根据数学公式，任意两点用直线公式表达为：

$\left(y_j-y_i\right)x+\left(x_i-x_j\right)y+x_j{y}_i-x_i{y}_j=0$ (3)

其中 $\left(x_i,y_i\right)$ 、 $\left(x_j,y_j\right)$ 为任意两节点坐标投影至二维的平面坐标，利用数学公式判断图3所示的两节点之间的连线与障碍物之间的位置关系，即圆心到直线的距离公式，A、B、C为该直线的具体参数：

$d=\frac{\left|A{x}_0+B{y}_0-C\right|}{\sqrt{A^2+B^2}}$ (4)

求出圆心到直线的距离后，将d与圆的半径比较，得出位置关系：

$\{\begin{array}{l}R>d障碍物与直线相交\\ R<d障碍物与直线相离\\ R=d障碍物与直线相切\end{array}$

(a) 节点连线与障碍物相切 (b) 节点连线与障碍物相交

Figure 3. The position relationship between the connections between nodes and obstacles

图3. 节点间连线与障碍物之间的位置关系

得到节点间联系与障碍物之间具体位置关系后，若相邻的两节点的连线与障碍区域相离，根据两点之间线段最短原则，连线AB便为无人机运行的最安全且最短的路径；若相邻的两节点与障碍区域相切见图3(a)或相交见图3(b)，为了安全起见，则以AB连线中点为圆心，以AB距离为直径做圆，将圆AB(包含障碍物区域)视作危险区域，无人机不得在此区域内飞行，所以安全节点的选取应该在圆AB以外。

5. 遗传算法规划

5.1. 遗传算法原理

遗传算法也称作进化算法，是受达尔文的进化论的启发，借鉴其中生物进化过程而提出的一种搜索算法 [12]。它的出现为路径搜寻提供新的思路和方案，在需要大范围搜寻最优解时，利用遗传算法从全局出发考虑，得到的结果也更有效和精准。在大自然中，生物为了适应环境，一直遵循着物竞天择、优胜劣汰原则，个体通过选择、交叉和变异基因来增强自己的生存能力，这样经过很多代的基因变化，最后得到的就是当前环境下适应度最好的基因。这样的一种生存原则被广泛运用于优化和搜索之中，找到一条最优路线。将初始种群通过一定的选择、交叉和变异，通过自身设置的适应度函数，使得优良的基因一代代遗传下去，这样进化N代后就很有可能会进化出适应度函数值很高的个体 [8]，将这些适应度函数值很高的个体，组成一个相对最优解的集合，把该集合内的所有个体进行比较，从而得到最优解 [13]。

5.2. 利用遗传算法模拟路径

在基于遗传算法的路径规划算法 [13] 中，每一个基因就是一个节点坐标即个体，与传统的二维栅格地图只能移动到当前位置邻近的栅格中不同的是，本文中的栅格地图种群中的个体由一系列坐标组成，并将这个点的x，y，z坐标分开进行存储，实现点与点之间的直接连接，并随意移动到任意一个位置，针对自行设置的初始种群个体利用轮盘赌算法，按照一定概率进行随机选择，对于被选择的个体按一定的几率进行交叉和变异，然后进行适应度计算，计算方法见公式4，完成一次迭代后从而得到新的种群，再重复上述步骤，直至迭代结束。经过第三部分中公式的计算，将所有相邻安全节点距离最短的节点规划出如图4所示的航迹图，将新的种群进行适应度值的计算与初始的种群进行比较，验证结果。

$\text{fitness}=1/D$ (5)

Figure 4. Flight trajectory diagram

图4. 飞行轨迹图

5.3. 基于遗传算法路径分析

本文中遗传算法的基本设置为种群规模为1000，染色体长度为100，迭代次数为100，利用轮盘赌选择的概率为0.5，变异率为0.2，交叉率为0.7，根据图1所处理好的地图模型，利用本文中的第二和第三章节中所给出的公式分析不同迭代次数的最短路径变化值。

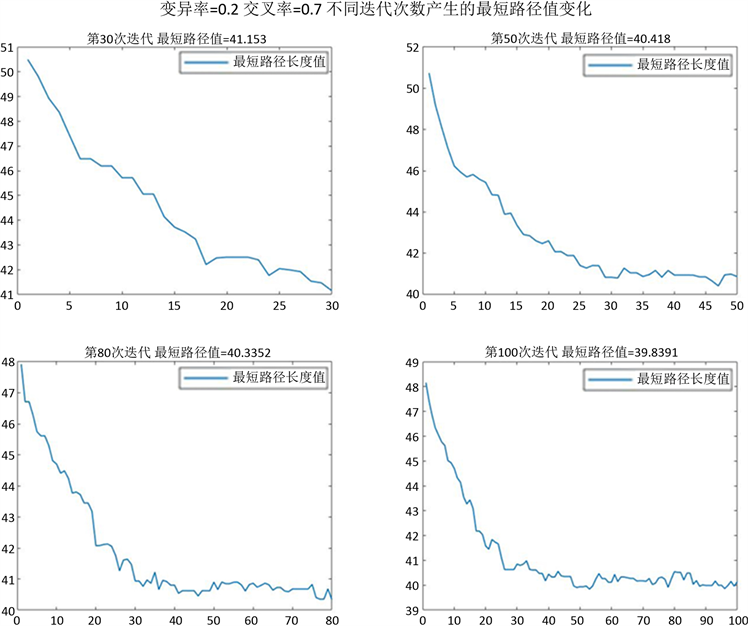
Figure 5. Evolution process diagram of genetic algorithm

图5. 遗传算法进化过程图

由图5可知，不同迭代的次数产生的最短路径值也不同，当迭代次数为30次时，最短路径值曲线一直在向下递减，并没有表现出缓和的趋势收敛速度非常慢，而当迭代次数分别为50次和80次时，进化曲线虽然有缓和的趋势，但这趋势并不明显且收敛速度也比较慢，因此在前三次的迭代次数中可知，当前迭代次数中并没有得到无人机航迹规划的最优解，而最后在100次迭代中，收敛速度非常快且随着迭代的次数增加，进化曲线也逐渐趋于缓和，因此可以认为，改进后的自适应遗传算法是有效的，最终得到最短路径是39.8。

6. 结论

利用遗传算法完成无人机避障路线规划，根据仿真结果得到以下结论：

1) 利用matlab模拟出障碍物三维形状，将整个三维地图进行网格化处理，便于找出每个点的坐标，且将每个点坐标分开存储，便于实现点与点间的直接连接，提高算法的运行效率。

2) 在模型迭代次数方面，在进行路径搜索最优解过程中，本文发现，以最短路径值为判断标准的进化曲线，当迭代次数越小，其收敛速度越慢，进化曲线越不稳定，而迭代次数越多，规划模型则表现出了更为优越的稳定性和收敛速度，通过该方案可以有效提升无人机在灾害救援任务中的响应能力以及救援效率。

尽管此次仿真结果较为满意，但实质上仍有不足，本文中将无人机自身的约束条件以及真实地理环境理想化，在实际运用中，还需要进一步的优化，所以如何让遗传算法在现实生活中发挥其优越的特性，是接下来的主要目标。

致谢

此论文是在王永虎教授的精心指导和大力支持下完成。

基金项目

重庆市技术创新与应用发展专项重点项目(cstc2019jscx-fxydX0036)。