半监督学习下的特征筛选问题研究

Research on Feature Selection under Semi-Supervised Learning

摘要: 相比于传统的监督学习算法，半监督学习下的特征筛选算法可以利用更多已知信息提高模型计算性能。本文利用样本特征的分位数推测总体特征的分布情况，基于无模型假设下给出相对稳健的半监督特征筛选结果，模拟发现该算法在标记样本量相对较少且各类样本量不均衡的情况下适用。实例借助TCGA中的肺腺癌(LUAD)和肺鳞癌(LUSC)数据集验证算法的有效性。

Abstract: Compared with the traditional supervised learning algorithm, the feature screening algorithm un-der semi-supervised learning can use more known information to improve the computational per-formance of the model. In this paper, the quantile of sample features is used to predict the distribu-tion of overall features, and a relatively robust semi-supervised feature screening result is given based on the model-free hypothesis. Simulation results show that this algorithm is applicable when the number of labeled samples is relatively small and the number of various samples is unbalanced. The effectiveness of the algorithm is verified by the data sets of lung adenocarcinoma (LUAD) and lung squamous cell carcinoma (LUSC) in TCGA.

1. 引言

随着“互联网+”时代的到来，人类活动所产生的数据正以指数级爆炸式增长，利用数据信息辅助研究人员实现更为可靠的决策判断成为人民生活的迫切需求。特征筛选是数据分析和数据挖掘中的重要环节，其意义不仅在于显著减少运算时间、提高模型效率、降低过拟合风险、使回归或判别预测模型更为适用等，而且在很多情况下筛选出的特征具有一定的可解释性和潜在研究价值。

当前主流特征筛选方法为边际筛选方法，即仅考虑单个特征对响应变量的影响，不考虑特征之间的关系和对响应变量的影响。该方向算法整体上的优势在于运算速度快，处理超高维特征时相比于传统方法在计算的复杂性、准确性以及稳定性上效果更好。最早是由Fan和Lv [1] 提出利用皮尔逊相关系数搭建SIS (Sure Independence Screening)算法，比较常用的有Li等 [2] 利用距离相关系数提出的DC (Distance Correlation)-SIS算法、Cui等 [3] 利用条件分布函数和无条件分布函数之间的加权差构造的MV (Market Value)算法以及Mai提出 [4] 利用Kolmogorov-Smirnov (KS)检验进行的特征筛选思想并拓展到多分类情况下得到融合Kolmogorov过滤器(Fused Kolmogorov Filter, FKF)算法 [5]。

仅用训练集中的特征和标签数据而忽略测试集中的特征数据是浪费的。这一问题在测试集中样本量远大于训练集中样本量时尤为突出。于是半监督学习应运而生，其常用思路可分为在无监督学习的基础上加入类别或成对约束和在监督学习的基础上加入特征之间的结构信息，目前已应用于图像处理和模式识别、音频语料分析、识别相关特征辅助医学诊断以及处理结构活性定量关系结构活性定量关系(Quantitative Structure Activity Relationship, QSAR)数据集辅助药物设计。He等 [6] 率先提出利用局部和整体特征结构的一致性建立了无监督特征选择拉普拉斯计分(Laplacian Score, LS)算法为后续研究打下了基础，Zhao等 [7] 将部分标签信息加入直接拓展至半监督领域得到LSDF (Locality Sensitive Discriminant Analysis)算法，Cheng等 [8] 则是在其基础上加入最小二乘和分类信息增益度(Classification Information Gain degree, CIG)构建GSFS (Graph-based Semi-supervised Feature Selection)算法，Sheikhpour等 [9] 针对回归问题基于Laplacian散点矩阵和正则化 $L_2$ 范数框架上提出SSCS (Semi-supervised Constraint Score)。

本文将Song等 [10] 在监督学习中的稳健加权分位数思想运用到半监督学习中，实现超高维数据下的半监督特征筛选问题，相比上述监督学习中的特征筛选算法具有更好的结果。

2. 半监督问题下的特征筛选算法

定义总体 $\left(X,Y\right)$，其中离散型响应变量Y有 $R_n$ 个类别 $\left\{y_1,\cdots ,y_{R_n}\right\}$，连续型特征变量 $X={\left(X_1,\cdots ,X_p\right)}^{\text{T}}$。从总体中抽取n个有类标签的样本组成的样本集 $L=\left\{\left(x_1,y_1\right),\cdots ,\left(x_n,y_n\right)\right\}$，剩下的 $N-n\left(N>n\right)$ 个无类标签样本组成样本集 $U=\left\{x_{n+1},\cdots ,x_N\right\}$，合并后得到总样本集 $T=L\cup U$。定义重要特征所在集合

$D=\left\{j:存在y=y_r,X_j与F\left(y|X_j\right)相关\right\}$,

与之对应的不重要特征集合为 $I=\left\{1,2,\cdots ,p\right\}\backslash D$。

定义第j个特征 $X_j$ 下的 $\alpha \left(0<\alpha <1\right)$ 分位数为 $Q_{\alpha }\left(X_j\right)\triangleq \inf \left\{t:P\left(X_j\le t\right)\ge \alpha \right\}$， $Y=y_r$ 下 $X_j$ 的 $\alpha$ 的分位数为 $Q_{\alpha }\left(X_j|Y=y_r\right)\triangleq \inf \left\{t:P\left(X_j\le t|Y=y_r\right)\ge \alpha \right\}$, $r=1,\cdots ,R_n$，Song等 [10] 在监督学习中综合得到加权分位指标 $w_j^{\alpha }\triangleq {\displaystyle {\sum }_{r=1}^{R_n}{p}_r{\left(Q_{\alpha }\left(X_j|Y=y_r\right)-Q_{\alpha }\left(X_j\right)\right)}^2}$，其中 $p_r=P\left(Y=y_r\right)$。又考虑到不能保证对任意 $\alpha$， $w_j^{\alpha }=0$ 有Y和 $X_j$ 是独立的，给出稳健加权分位数

$w_j={\displaystyle {\int }_0^1{\displaystyle \underset{r=1}{\overset{R_n}{\sum }}{p}_r{\left(Q_{\alpha }\left(X_j|Y=y_r\right)-Q_{\alpha }\left(X_j\right)\right)}^2\text{d}\alpha }},j=1,\cdots ,p$. (1)

本文将公式(1)从监督学习背景推广至半监督学习，多个分位点取代连续型积分。取 $M=10$ 对区间 $\left[0,1\right]$ 进行切片，此时可给出利用数据估计的半监督稳健加权分位数(Semi-supervised Robust Composite Weighted Quantile, SRCWQ)

${\hat{w}}_j^{\left(Q\right)}=\frac{1}{M}{\displaystyle \underset{k=1}{\overset{M}{\sum }}{\displaystyle \underset{r=1}{\overset{R_n}{\sum }}{\hat{p}}_r{\left({\hat{Q}}_{{\alpha }_k}^L\left(X_j|Y=y_r\right)-{\hat{Q}}_{{\alpha }_k}^T\left(X_j\right)\right)}^2}}$, (2)

其中， ${\alpha }_k=\left(0.5+k-1\right)/M,k=1,\cdots ,M$， ${\hat{p}}_r=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}I\left\{Y=y_r\right\}}$。总样本集T下经验分布函数为 ${\hat{F}}_{N,X_j}\left(x\right)\triangleq \frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}I\left\{X_{ij}\le x\right\}}$，则对应分位数为 ${\hat{Q}}_{{\alpha }_k}^T\left(X_j\right)\triangleq {\hat{F}}_{N,X_j}^{-1}\left({\alpha }_k\right)$ ；已标记样本集L下经验条件分布函数为 ${\hat{F}}_{n,X_j|Y=y_r}\left(x\right)\triangleq \frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}I\left\{X_{ij}\le x,Y=y_r\right\}}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}I\left\{Y=y_r\right\}}}$，对应分位数 ${\hat{Q}}_{{\alpha }_k}^L(X_j|Y=y_r)\stackrel{\Delta }{=}{\hat{F}}_{n,X_j|Y=y_r}^{-1}({\alpha }_k)$。

本文根据按照从大到小的顺序对p个特征的SRCWQ指标值进行排序，取前 $d=\left[n/\log \left(n\right)\right]$ 个组成重要特征集合D即为特征筛选所得结果。

3. 数值模拟

本文采用蒙特卡洛算法进行模拟，目标是对比不同情况下不同算法的特征筛选方法优劣。

取响应变量 $Y=0$ 或1，其中 $Y=y_r$ 下有重要特征 ${\tau }_{y_r}$， $X_i={\mu }_{{\tau }_{y_r}}+{\epsilon }_i$， ${\mu }_{{\tau }_{y_r}}$ 即表示除第 ${\tau }_{y_r}$ 个为1其余均为0的p维向量， $\epsilon ~N\left(0,\Sigma \right),\Sigma =I_p$。设置默认参数：随机数种子100、已标记样本量个数 $n=50$ 、总样本量个数 $N=300$ 、重抽样次数 $B=200$，特征维数 $p=2000$ 以及均衡状态 $P\left(Y=0\right)=P\left(Y=1\right)$。

将本文提出的半监督学习算法SRCWQ与传统监督学习算法DC [2]、MV [3] 以及FKF [5] 进行对比，利用以上参数构造模型1，从均衡状态、异常值以及协方差三个角度修改参数得到模型2~4。其中，模型2修改模型1中均衡状态为 $P\left(Y=0\right):P\left(Y=1\right)=4:1$，模型3为模型1中增加4个异常点，模型4修改模型1中协方差 $\Sigma ={\left({\sigma }_{ab}\right)}_{p\times p},{\sigma }_{ab}={0.3}^{\left|a-b\right|},1\le a,b\le p$。

构造模型的评价指标 $MMS\left(a\right)$ 、RSD、 $P_k$ 以及 $P_a$。在 $B=200$ 次循环中，每一次选中全部重要特征所需要选择的特征数量为 $MM{S}_b\left(a\right),b=1,\cdots ,B$，RSD为 $MMS\left(a\right)$ 上下四分位数之差除以1.34，表示特征筛选结果的稳定性； $P_k$ 表示在前 $d=\left[n/\log \left(n\right)\right]$ 个所选特征中包含第k个重要特征的比例， $P_a$ 表示在前 $d=\left[n/\log \left(n\right)\right]$ 个所选特征中包含全部重要特征的比例。根据上述定义， $MMS\left(a\right)$ 和RSD的数值越小越好，而 $P_k$ 和 $P_a$ 则是越大越好。表1利用上述指标给出不同算法下不同模型的特征筛选结果情况，可以看到在样本不均衡分布和存在异常点时效果较好。

Table 1. Summary of feature screening results under different algorithms

表1. 不同算法下特征筛选结果情况汇总

4. 实例分析

本文利用公开数据集TCGA中肺腺癌(LUAD)和肺鳞癌(LUSC)的基因表达RNA序列数据集构造半监督数据集。原始数据来源于网址https://gdc.xenahubs.net，仅提取尾号为“01A”(表示患病)和“11A”(表示正常)的样本。考虑到基因探针信息一致，两数据集可以进行合并，总特征个数 $p=60488$，其中60483个为基因编号，5个样本基因评价指标分别为alignment_not_unique (比对位置不唯一)、ambiguous (比对区域与多个基因都发生重叠)、no_feature (比对区域与任何基因都没有重叠)、not_aligned (无法比对上)以及too_low_aQual (比对质量低于设定阈值，默认是10)。从数据集中的样本名称提取活体组织检测结果，得到样本分类LUAD (对应类别1)、LUSC (对应类别2)以及Normal (正常，对应类别0)共3种情况，每类样本量分别为510、496以及107。于是可得总样本集T中样本量 $N=1113$，按照类样本比例抽取5%的样本构成已标记样本集L，筛选特征个数 $d=13$，重复抽样实验200次降低偶然性。

Table 2. Confusion matrix under three categories

表2. 三分类下的混淆矩阵

构造三分类混淆矩阵如表2所示，给出模型评价指标定义如下：

· 正确率： $\left(a_1+a_5+a_9\right)/\left(a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8+a_9\right)$，表示模型分类性能，得分越高越好。

· LUAD误诊率： $1-a_5/\left(a_4+a_5+a_6\right)$，表示样本患LUAD但是诊断错误的概率，得分越低越好。

· LUSC误诊率： $1-a_9/\left(a_7+a_8+a_9\right)$，表示样本患LUSC但是诊断错误的概率，得分越低越好。

· LUAD和LUSC误诊率： $1-\left(a_5+a_9\right)/\left(a_5+a_6+a_8+a_9\right)$，表示样本患LUAD但被诊断为LUSC或样本患LUSC但被诊断为LUAD的概率，得分越低越好。

· 是否患病误诊率： $\left(a_2+a_3+a_4+a_7\right)/\left(a_1+a_2+a_3+a_4+a_5+a_6+a_7+a_8+a_9\right)$，表示样本患病但未被诊断出患病或样本不患病但被诊断出患病的概率，得分越低越好。

给出200次抽样实验中，每次选中的前13个特征结果。对特征频次进行从大到小排序后，选择前13个特征进行200次随机森林分类，给出每次分类下正确率结果，每个模型情况如图1(a)所示。其中可以看到SRCWQ在单次分类准确率和稳定性上优于其它算法。该算法下筛选出的重要基因如图1(b)所示，认为若该基因出现频次越高，则致病可能性越大。

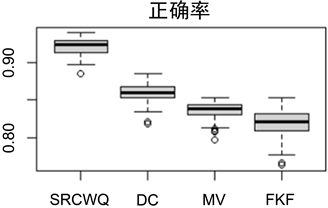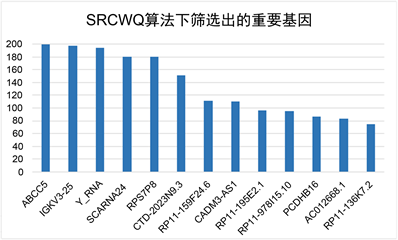(a) (b)

Figure 1. Schematic diagram of model evaluation under different algorithms

图1. 不同算法下的模型评价结果示意图

考虑到现实生活中数据的不完整性，对200次抽样实验中的每一次特征筛选结果做一次随机森林分类，给出每次分类下的误诊率如图2所示，从中可以看到SRCWQ相比于其它算法有更少的可能会出现误诊情况，尤其在是否患病的情况下较为突出。

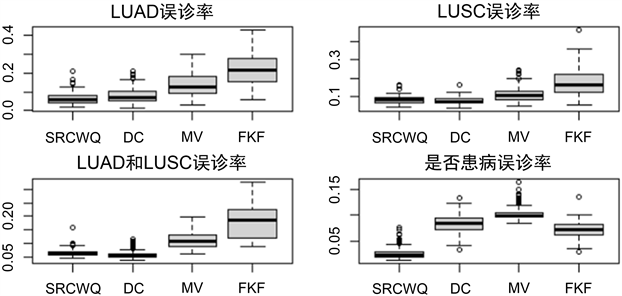
Figure 2. Misdiagnosis rate under different algorithms

图2. 不同算法下的误诊率

5. 总结

综上，本文在Song等 [10] 基础上进行拓展，利用样本特征的分位数分布，提出了一种半监督学习下的特征筛选方法SRCWQ。经数值模拟验证，该算法在已标记样本量显著小于总样本量下，针对各类样本量不均衡或存在异常点的情况较为适用。经实例验证，该算法可借助大量无标记样本，对罕见病诊疗有一定的辅助判断作用。