基于粒子滤波和主成分分析优化的极限学习机在风电场功率预测的应用

Application of Extreme Learning Machine Based on PF and PCA Optimization in Wind Farm Power Prediction

摘要: 风力发电的波动性给实现电网安全运行带来了挑战，因此，需要准确预测风力发电量。提出了一种基于粒子滤波和单隐层神经网络极值学习机的短期风电预测方法，并引入主成分分析对数据进行降维。极限学习机具有快速的训练速度和良好的泛化性能，它可以在同一时间和空间学习风速、风向等气象因素与海上风电场发电量之间的关系，再加上粒子滤波对数据的预处理，更新训练数据和网络结构。实现气象数据的快速实时校正和风电机组输出功率预测。与现有预测规模型相比，本实验模型平均绝对百分比误差最低为5.81%，结果验证了所提预测方法的可行性和优越性。

Abstract: The volatile nature of wind power generation creates challenges in achieving secure power grid op-erations, therefore, necessary to accurately predict wind power. This study proposes a short- term wind power prediction method based on Particle Filter and single hidden layer neural network Ex-treme Learning Machine and introduces Principal Component Analysis to reduce the dimensionality of the data. ELM has a fast training speed and good generalization performance, it can learn the re-lationship between wind speed, wind direction and other meteorological factors and power genera-tion in offshore wind farms at the same time and space, coupled with the preprocessing of the data by the Particle Filter, update training data and network structure. Realize rapid real-time correc-tion of meteorological data and wind turbine output power prediction. Compared with the existing prediction scale model, the average absolute percentage error of the experimental model is 5.81%, comprehensive results validated the feasibility and superiority of the proposed prediction ap-proach.

1. 引言

随着“碳达峰 [1] ”理论的提出，包括风电在内的清洁能源在整个电网能源供给中占的比重越来越大，很多问题也随着大规模风电的并网而带入电网系统中 [2] [3] [4] 。2014年中国能源局出台的《风电功率预测系统功能规范》 [5] 对预测时间提出了明确要求：短期预测应能预测未来至少3天内的风电输出功率，时间分辨率不小于15 min。

风机发电功率预测，按时间尺度可以分为长期预测、中期预测、短期预测和特短期预测 [6] ；按预测方法可分为物理方法、统计方法或二者相结合的方法。运用物理方法进行风机功率预测，需要涉及的建模对象很多，例如，需要风机所在地周围的障碍物、温度以及等高线等信息作为参考进行分析。利用统计方法来建立预测模型，实质是建立系统输入与风电功率之间的映射关系，可以直接利用气象数据对发电功率进行预测。主要方法有神经网络、粒子群算法、灰色理论算法和支持向量机等 [7] [8] [9] [10] 。在人工神经元网络算法中，反向神经网络和卷积神经网络有较强的非线性辨识能力，但是其学习速度慢、容易陷入局部最优解等问题，不能广泛适用于实际工作需求。针对这种情况Huang [11] 提出一种新型单隐层前馈神经网络算法，称为极限学习机(Extreme Learning Machine, ELM)，极限学习机只需要设置网络的隐层节点个数，随机生成输入权重和偏差 [12] ，求解输出权重矩阵，而不需要重复迭代地调整输入权值和隐含层偏置，因此计算量和时间复杂度都会小很多，在复杂问题上具有学习速度快且泛化性能好的优点 [13] [14] 。这就是ELM优于其他传统神经网络和机器学习算法的关键所在。已被应用于研究许多工程问题求解中。在电力工程领域，ELM及其扩展算法在实时电价预测 [15] 、电力系统暂态稳定在线评估 [16] 等方面都取得了不错的效果。

我们经过多次实验发现，多维度的气象参数数据是庞大的，而且测风塔数据也存在坏点，采用粗犷的全盘接收不仅浪费大量的资源，更会直接降低训练结果的精确度，因此，为节约计算资源，提高运算速度和模型精确度，需要对数据进行滤波优化和特征选择。所以本文引入了粒子滤波(Particle filter, PF)和主成分分析法(Principal Component Analysis, PCA)。

综上所述，本文提出一种结合ELM算法、主成分分析和粒子滤波的单隐层前馈神经元网络风电功率预测方法，解决ELM算法精度不高，输入参数庞大的问题，使用平均绝对误差(Mean Absolute Error)和平均绝对百分比误差(Mean Absolute Percentage Error)对预测结果全面评估，通过对英国某大型风电场的输出功率的短期预测仿真验证，与ELM传统算法、粒子群算法、GA-BP神经网络等主流预测算法相对比，证明预测方法的有效性。

2. 模型建立

2.1. PF算法原理

粒子滤波器算法是一种基于贝叶斯估计和蒙特卡罗方法的在线非线性识别算法。其本质是通过寻找在状态空间中传播的一组随机样本来近似状态概率密度函数。

粒子滤波具体步骤如下 [17] ：

Step 1，初始化数据

从初始分布 $p\left(X_0\right)$ 采样N个数据本： $\left\{x_0\left(i\right),i=1,2,\cdots ,N\right\}$ ，权值设置为 $w_0\left(i\right)=1/N$ ，令 $k=1$ 。

Step 2，重要性采样

1) 采样 $\left\{x_k\left(i\right),i=1,2,\cdots ,N\right\}$ 得N个k时刻样本。

2) 观测值到来时，计算每个粒子的权值，并由式(1)更新权值并进行权值归一化。

$w_k^{\text{*}}\left(x_{0:k}\right)=w_{k-1}^{\text{*}}\left(x_{0:k-1}\right)\frac{p\left(y_k|x_k\right)p\left(x_k|x_{k-1}\right)}{q\left(x_k|x_{0,k-1},y_{1:k}\right)}$ (1)

Step 3，后验估计

计算有效粒子数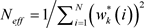，，若 $N_{e\pi }\le N_T$ 设定粒子数，执行第四步；否则执行第五步。

Step 4，重采样

依据权值大小采样新粒子 $x_k\left(i\right)$ ，使其满足 $p\left(x_k\left(\hat{i}\right)=x_k\left(i\right)\right)=w_k\left(i\right)$ ，设定 $x_k\left(\hat{i}\right)=x_k\left(i\right),w_k\left(i\right)=1/N$ 。

Step 5，风速数据滤波输出

按如下公式进行风速数据滤波输出，如公式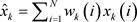(2)：

(2)

Step 6，继续滤波

继续下一个值滤波，令 $k=k+1$ ，返回第二步。具体粒子滤波工作流程如下图1：

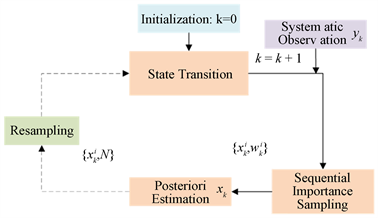
Figure 1. Basic steps of particle filter

图1. 粒子滤波流程图

2.2. PCA-ELM预测算法

2.2.1. PCA算法原理

PCA用于优化ELM处理数据简单粗放致使其预测精度不高的缺点，其主要思想是在信息损失很少的情况下，基于线性变换，用一些新的独立主成分代替原始数据多维变量 [18] 。首先对滤波数据进行标准化处理如式(3)，以消除不同维度带来的不利影响，构建数据矩阵，设 $X_{mn}$ 是带有m个样本，n个风功率影响因素数据样本矩阵，即 $X_{mn}=\left(X_1,X_2,\cdots ,X_j,\cdots ,X_n\right)$ ，其中 $X_j={\left(x_{1j},x_{2j},\cdots ,x_{xj},\cdots ,x_{mj}\right)}^{\text{T}}$ 。

$x_{ij}^{\text{*}}=\frac{x_{ij}-{\bar{x}}_j}{S_j},i=1,2,\cdots ,m;j=1,2,\cdots ,n$ (3)

式中： ${\bar{x}}_j$ 为均值； $S_j$ 为方差。

然后需要计算相关系数矩阵及其特征值和特征向量，确定累积贡献率和主成分的表达式。主成分的选取标准一般采用累计方差贡献率，如式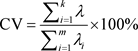(4)。

(4)

其中，CV为累计方差贡献率， ${\lambda }_i$ 为协方差矩阵的第i个特征值，且特征值满足 ${\lambda }_1>{\lambda }_2>\cdots >{\lambda }_m$ 。

计算该矩阵的协方差矩阵，并求解其特征值 $\lambda$ ，根据式(4)计算主成分的累积贡献率CV，通常 $C{V}_i\ge 90\%$ ，选取前k个累积贡献率大于90%的主成分的特征向量构成投影矩阵 $a$ ，根据式(5)计算降维后的主成分：

$\{\begin{array}{c}{P}_1=a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n\\ P_2=a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n\\ \cdots \\ P_k=a_{k1}{x}_1+a_{k2}{x}_2+\cdots +a_{kn}{x}_n\end{array}$ (5)

式中： $x_n$ 为标准化处理后的气象因素； $P_k$ 为降维后的主成分； $a_{kn}$ 为主成分的系数。

2.2.2. ELM算法原理

ELM是一种新型的快速学习算法，分为两个主要阶段：1) 随机特征映射2) 线性参数求解。第一阶段，隐含层参数随机进行初始化，然后采用非线性映射作为激活函数，将输入数据映射到一个新的特征空间(称为ELM特征空间)。为了达到选择最佳激活函数的目标，对不同激活函数进行训练，发现“Sigmoid”激活函数有着最短的平均训练时间，并且拥有不弱于其他激活函数的运算精度，更加适用于ELM风功率预测，故选择其为激活函数。

设有N个任意样本 $\left(X_i,t_i\right)$ ，其中 $X_i={\left[x_{i1},x_{i2},\cdots ,x_{in}\right]}^{\text{T}}\in R^n$ ， $t_i={\left[t_{i1},t_{i2},\cdots ,t_{im}\right]}^{\text{T}}\in R^m$ 。对于单隐层神

经网络，ELM可以随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值。对于一个单隐层神经网络，主要网络模型表达式 [19] 如式(6)：

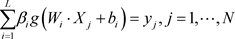(6)

式中： $W_i$ 为输入层节点和第i个隐含层节点之间连接的输入权重向量； ${\beta }_i$ 为第i个隐含层节点和输出层节点之间连接的输出权重向量； $b_i$ 为第i个隐含层节点的阈值； $y_j$ 为网络模型的实际输出； $g\left(W_i\cdot X_j+b_i\right)$ 为激活函数。

上式可以用矩阵表示为：

$H\beta =T$ (7)

对于一个有L个隐含层节点的单隐层神经网络学习的目标是使得输出的误差最小，可以表示为式(8)：

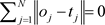(8)

即存在 ${\beta }_i$ ， ${\omega }_i$ 和 $b_i$ ，使得式(7)可以用矩阵表示为：

$H\left(W_1,\cdots ,W_L,b_1,\cdots ,b_L,X_1,\cdots ,X_L\right)={\left[\begin{array}{ccc}g\left(W_1\cdot X_1+b_1\right)& \cdots & g\left(W_L\cdot X_1+b_L\right)\\ ⋮& \cdots & ⋮\\ g\left(W_1\cdot X_N+b_1\right)& \cdots & g\left(W_L\cdot X_N+b_L\right)\end{array}\right]}_{N\times L}$ (9)

$\beta ={\left[\begin{array}{c}{\beta }_1^{\text{T}}\\ ⋮\\ {\beta }_L^{\text{T}}\end{array}\right]}_{L\times m,}T={\left[\begin{array}{c}{T}_1^{\text{T}}\\ ⋮\\ T_N^{\text{T}}\end{array}\right]}_{N\times m}$ (10)

经过第一阶段 $w,b$ 已随机产生而确定下来，由此可根据公式(9)和(10)计算出隐含层输出H。

在ELM学习的第二阶段，只需要求解输出层的权值 $\beta$ 。为了得到在训练样本集上具有良好效果的 $\beta$ ，需要保证其训练误差最小，可以用 ${\rm H}\beta$ 与样本标签T求最小化平方差作为评价训练误差(目标函数)，使得该目标函数最小的解就是最优解 [20] 。

2.3. 神经网络模型构建

本文首先提出了基于PF-PCA-ELM的风电功率预测模型，经过粒子滤波处理后的数据无需更改格式即可输入到PCA-ELM预测模型中，但经PCA降维后的修正气象数据需要进行归一化处理，生成修正风速、风向正弦、风向余弦、空气密度，将其设为输入，风力发电厂SCADA (Supervisory Control and Data Acquisition，监控与数据采集系统)系统实测输出功率为输出，此处采取如图2网络所示的PF-PCA-ELM核心算法模型来模拟修正风速和风功率的非线性关系。

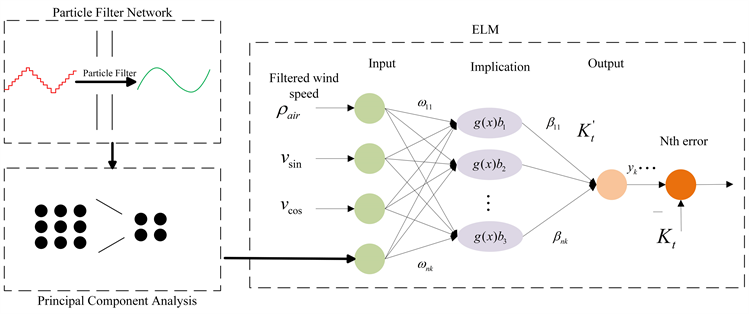
Figure 2. PF-PCA-ELM model structure

图2. PF-PCA-ELM模型结构

图中 ${\omega }_{11}\text{~}{\omega }_{nk}$ 为输入层与隐含层之间的权重； $g\left(x\right)$ 为激活函数； $b_1~b_k$ 为隐含层节点阈值； ${\beta }_{11}\text{~}{\beta }_{nk}$ 为隐含层与输出层之间的权重； $y_k$ 为第k次发电功率输出。

3. 实例分析

本文利用MATLAB R2019b软件进行实验，通过NOAA实验室下Hourly/Sub-Hourly observational Data平台(该平台会公布全球各地观测点历年某一时间段的相关气象数据)采集英国爱尔兰海域West Duddon海上风电场附近测风塔从2019年1月1号至2019年1月12号的气象数据，如图3，所有数据的时间分辨率均为1h，预测的时间分辨率与此一致。风力机发电功率数据来自该风电场SCADA系统获取的实测输出功率，所得输出功率时间线与气象数据一致。本文将前228个数据设为A组(训练集)，将后面的72个数据设为B组(测试集)，部分气象数据如表1。

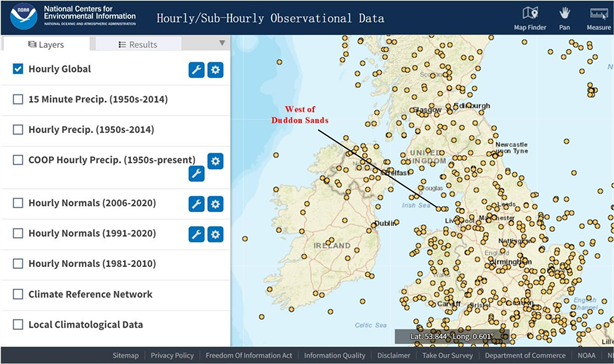
Figure 3. Hourly/Sub-Hourly observational Data platform

图3. Hourly/Sub-Hourly observational Data平台

Table 1. Partial meteorological training data

表1. 部分气象训练数据表

根据常见风电机组功率输出特性曲线，在中风速段(切入风速至额定风速)，较小的风速变化会引起明显的输出功率变化，并且通过监测系统得出的数据有漏测或误测等情况出现，下面将利用粒子滤波法对坏数据进行剔除、填补缺漏数据，表2和表3分别给出了风电场各个测量参数的合理变化范围，可以帮助判断过滤后数据的稳定性。

Table 2. Reasonable range of wind farm measurement parameters

表2. 风电场测量参数合理范围

Table 3. Reasonable variation range of wind farm measurement parameters

表3. 风电场测量参数的合理变化范围

4. 算法性能比较

4.1. 激活函数选择

激活函数(Activation functions)是极限学习机中重要的组成环节。在隐含层中，将激活函数应用于输入与权重的乘积，并将结果送入下一层。目前，主流激活函数主要分为Sigmoid函数、双曲正切函数(Tanh)和线性修正单元(ReLu)，为选择最适合ELM风功率预测的激活函数，我们设置多组对照实验，用ELM算法搭载三种不同激活函数并与GA-BP算法进行同步对比，实验结果如下表4：

Table 4. Computing comparison of activation function

表4. 不同激活函数性能对比

根据上表以及实验表现来看，传统的Sigmoid函数在所有激活函数中表现，虽然在计算速度上与Tanh和ReLu相差不大，但是其平均绝对百分比误差优于其余两位。需要注意的是，虽然ReLu函数可以有效地避免和纠正梯度消失问题，但由于气象数据具有起始点不为0且波动较为明显的特征，致使ReLu函数并不能很好地发挥作用。

4.2. PF-ELM模型

在建立模型的早期，没有添加主成分分析方法，而是直接建立PF-ELM模型。只使用PF对数据进行预处理，对初始数据集进行去噪并导入极限学习机。通过实验验证发现，基于PF-ELM模型的风电功率预测计算时间并不比GA-BP模型短很多，最重要的是它的预测精度远低于主流算法。实验结果如下图4所示：

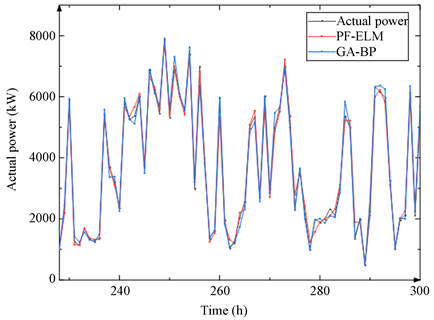
Figure 4. Comparison of PF-ELM and GA-BP results

图4. PF-ELM和GA-BP结果比较

4.3. PF-PCA-ELM模型

最初的模型没有得到预期的结果，所以本文仔细分析了相关原因：极限学习机导入了过多的气象参数，然而有些参数不利于风功率的预测，计算机的处理能力有限，导致模型性能下降。针对这个问题，本文建立了PF-PCA-ELM模型，在PF-ELM模型中加入主成分分析，过滤出气象变量的最优子集，减少修正后的误差，缩短计算时间。从气象数据获取到实验结果获取的PF-PCA-ELM模型实验流程图如图5所示：

Figure 5. Flow chart of PF-PCA-ELM prediction model

图5. PF-PCA-ELM预测模型实验流程图

5. 结果分析

5.1. 滤波结果分析

对于A组数据，将滤波过程中的过程噪声和观测噪声设置为[0,2]间的随机值，设粒子数目为300，数据滤波前后对比如图6。

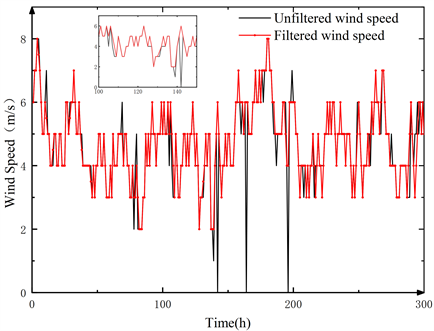
Figure 6. Comparison of data before and after filtering

图6. 数据滤波前后对比

由图可以看出，在148 h、161 h和195 h时原始数据有坏点，粒子滤波可以有效的根据坏点前后数据变化趋势做出合理修正；从整体来看，将过程噪声和观测噪声的范围设置在[0,2]之间即保留了绝大部分原始气象数据，又对噪点和坏点进行了弥补。对比滤波前后风速的变化范围，提高了数据的可靠性，填补了部分测量数据的漏缺，保持了数据的完整性。

Figure 7. Actual power generation and predicted power generation

图7. 实际发电功率与PF-PCA-ELM预测发电功率对比

5.2. 发电功率预测结果

将预处理过后的数据通过归一化操作后，输入ELM的功率预测网络模型，训练得出输入层权值和阈值，输出层权重则通过广义逆矩阵理论计算得到。所有网络节点上的权值和阈值得到后，极限学习机的训练就完成了，此时可以利用调试好的模型参数对B组数据集进行测试，利用刚刚求得的输出层权重便可通过网络运算得到最终的预测数据，如图7。

将通过算法所得预测数据和原始数据作对照，计算其百分比误差和绝对误差如图8。

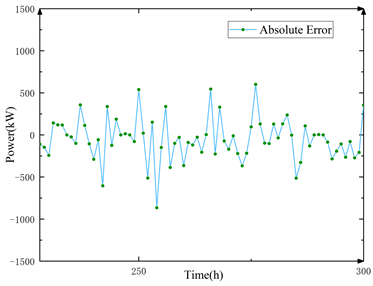
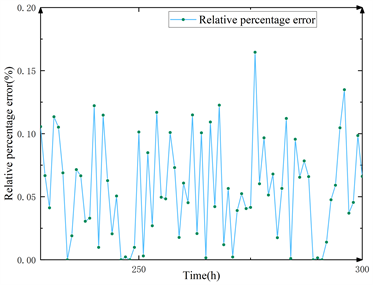(a) 绝对误差 (b) 百分比误差

Figure 8. Absolute error and percentage error

图8. 绝对误差与百分比误差

从图中可得到：本模型每一个数据点的预测结果绝对误差在7%上下浮动，在300个数据点中，只有1个数据点百分比误差超过了15%，此点在270 h附近，其原因为在次点之前的250 h~270 h，风速急剧变化，从2.5 m/s跃迁至7 m/s，后续迭代均在此基础上展开，但风速又突然降低，在4 h内又降回2.5 m/s，这为机器学习带来了很大的困难，其余算法模型在此点也出现较大误差，除此之外，图中近一半的数据点误差保持在5%以下；可以看到在280 h~300 h时，百分比误差出现大范围波动，但绝对误差却不明显，这是因为在此时间段风速等气象数据变化剧烈，但其数值较小，在4 m/s~6 m/s之间波动，所以风功率的实际误差数值也只在200 Kw~300 Kw间浮动；从绝对误差图可以看出本模型预测性能稳定，没有出现明显的坏点和失真情况。

5.3. 综合比较

为进一步测试算法性能，本文与不同类型的算法进行了比较，其中包括传统ELM、粒子群算法、GA-BP神经网络算法，采取相同的数据指标，从平均绝对误差、平均绝对百分比误差和计算时间三方面横向对比各算法的优缺点。MAE和MAPE计算公式如式(15)和式(16)。

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|{\hat{y}}_i-y_i\right|}$ (15)

$\text{MAPE}=\frac{100\%}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|}$ (16)

MAPE数值范围为 $\left[0,+\infty \right)$ ，其值越小，则预测结果越好。

从图9中可以得到：风电功率具有非平稳性，PF-PCA-ELM模型相比于PSO、GA-BP模型，增加了粒子滤波树立，减少了噪点的干扰，使预测曲线更加流畅，没有出现“断崖式”上升或下降的大幅度功率变化，实验结果更加贴近实际功率曲线；而观察PSO曲线可以看到，在气象数据缺失点，其所得实验结果出现大幅偏差，而且在255 h、290 h等非缺失点依然出现上述情况，其原因为针对多个局部极值点的函数，PSO并不能收敛至全局最优，在类似于风功率预测等少量参数维度的问题上其算法并不完善；在处理平稳变化的气象数据处理方面，例如242 h~255 h，除个别数据点ELM和PSO出现失真情况外，5种算法的预测准确度均保持的较好；在急速变化的气象数据处理方面，例如280 h~300 h，ELM已不能很好地胜任预测工作，而PF-ELM和PSO算法处理急速变化数据的能力较弱，对于GA-BP算法，由于有着遗传算法对神经网络初始权值和阈值选择的优化，增强了全局寻优能力，使其在不断快速变化的数据输入方面依旧有着不俗的精度，而PF-PCA-ELM模型则是依靠强大的数据处理能力以及对初始权值和阈值没有较高要求的特点，也保持较高的准确度。

Figure 9. Comparison of prediction results of different algorithms

图9. 不同算法预测结果比较

从表5可以得到：在预测精度方面，PF-PCA-ELM模型和GA-BP模型预测误差相当，MAPE值都约等于5.8%，平均绝对误差只有124KW和128KW；PSO算法误差稍大达到了8.2%，误差最大的是未经优化的ELM算法，达到了12.6%，平均绝对误差达到283.85 KW。在运算时间方面，尽管GA遗传算法已经对BP神经网络中的初始权值和阈值选择进行了优化，但是BP神经网络具有天然的运算速度慢的问题，需要大量的训练学习才能运行，而这一点GA遗传算法没有很好的解决，经实验表明GA优化BP神经网络的迭代次数较大，这也就导致了其运算时间高于PSO，是PF-PCA-ELM模型的200.51%；对于PF-PCA-ELM模型，虽然在ELM的基础上增加了粒子滤波环节，同时也融入了PCA主成分分析，但是由于ELM算法隐含层节点的权重为随机或人为给定的，且不需要更新，学习过程仅计算输出权重，具有泛化能力强、学习速率快等特有的优点，使本文模型不仅保留了极限学习机迭代速度快的特点而且增强了算法的稳定性和预测精度，本文提出的方法与其他4种方法相比，虽然高预测精度的优势较为突出，但在运算速度方面PF-PCA-ELM模型具有显著的优势，极大地节省了计算资源。

Table 5. Comparison of root mean square error and operation time

表5. 均方根误差和运行时间对比

6. 结论

本文针对风电功率波动性大、预测精度和计算时间差等问题提出一种基于PE-PCA-ELM集成学习模型的风电功率预测方法。对比不同的预测算法，得出以下结论：

1) PCA法能较好地解决自变量冗余、因数据量大而产生的过度迭代等问题，基于此的预测网络对历史数据信息具有更强的预测特征提取能力，可有效提高风速序列的预测精度；

2) 本试验方法相比粒子群算法、BP神经网络算法在计算速度上具有明显优势。在对大量数据进行预测和处理时，可以更快地对实时数据进行在线预测，节省大量时间；

3) 节省计算资源，减少对风功率预测条件的需求，由于获取气象数据的限制，本文只选取了约12天的气象数据，但实际工作需求中所处理的数据量将达到几千甚至上万级别，数据量越庞大越需要大量的计算资源，本方法大大减少了计算资源，普通性能处理器就能胜任短时间处理大量数据工作；

4) 对于有坏点或缺失数据的原始数据，该算法比主流算法更稳定。它为风能预测问题提供了一种新的解决方案。

参考文献