单线激光点云拼接SLAM算法研究

Research on Single Line Laser Point Cloud Splicing SLAM Algorithm

摘要: 针对传统单线激光SLAM算法，在地图构建过程中，由于单线激光单帧点云数据量过少，在某些局部相似的场景中可能出现得分很高的误匹配情况，本文对点云配准算法的迭代环节经行改进，并提出一种滑动窗口的点云拼接方法，利用新拼接的点云组，进行地图构建和回环检测。分别在仿真与实际环境中对本文所提算法经行验证，在仿真环境中本文改进的点云配准算法相对于原来的点云配准算法，迭代次数减少50.22%，运行时间减少39.67%；在真实环境中利用机器人平台进行定位与地图构建，结果表明本文所提算法在定位精度、建图精度和实时性上提升明显，可以有效解决单线激光运行过程中的误匹配情况。

Abstract: Aiming at the traditional single-line laser SLAM algorithm, in the process of map construction, due to the small amount of single-line laser single-frame point cloud data, there may be mismatches with high scores in some locally similar scenes. In this paper, the iterative link of the point cloud registration algorithm is improved, and a sliding window point cloud splicing method is proposed. Using the newly spliced point cloud group, we carry out map construction and loop detection. The proposed algorithm was verified in simulation and real environment respectively. In the simulation environment, compared with the original point cloud registration algorithm, the iteration times and running time of the improved point cloud registration algorithm were reduced by 50.22% and 39.67%. In the real environment, the robot platform is used for positioning and map construction. The results show that the proposed algorithm improves the positioning accuracy, map construction accuracy and real-time performance significantly, and can effectively solve the mismatching situa-tion during the operation of single line laser.

1. 引言

当机器人处于一个未知环境时，为使移动机器人实现自主行走，必须同时解决定位和地图创建问题，也称(Simultaneous Localization and Mapping, SLAM) [1] 问题。激光SLAM [2] [3] 是机器人根据其所携带的激光传感器，确定自身在地图中的位置及姿态，实现机器人自主行走。单线激光SLAM [4] [5] 中由于单帧激光点云数据量过少，在某些局部相似的场景中可能出现得分很高的误匹配情况。针对这个问题，文献 [6] 在激光传感器的基础上，引入惯性测量单元(Inertial Measurement Unit, IMU)，通过IMU获得两个扫描点云的初始位姿估计，并提取两个二维点集的线特征来完成快速变化场景的匹配，减少误匹配情况。文献 [7] 将激光扫描点利用金字塔采样得到不同分辨率的概率网格，提高匹配效率，进一步的减少了局部的累计误差，但增加了计算量。文献 [8] 结合WiFi定位，对WiFi信号强度加权匹配，利用卡尔曼滤波器实现激光雷达与WiFi的融合定位结果。文献 [9] 根据机械雷达的固有特性，在匹配阶段，只查找相邻两条激光线之间的内点，提高了近邻点索引的精度和效率。这些方法都在一定程度上提高了算法精度，但都存在一个问题，引入其他传感器或者改进匹配方式都增大了计算量，需要性能更高的硬件平台才能保证SLAM系统的实时性。为此本文在不引入其他传感器和不提高硬件平台性能的前提下，对单线激光雷达的多帧激光点云进行拼接使得有效点云数目增多，获得更多的环境信息，提高地图构建与回环检测的精度。

本文算法流程分为以下几步，首先将传感器数据预处理去除噪声点，然后利用点云配准的算法计算出相邻帧之间的位姿，再对点云进行拼接，点云的拼接提出一种滑动窗口拼接的方法，因为激光频率很高，可以在一秒钟提取一帧激光数据，十秒为一组实时更新拼接点云，在室内低速运动场景下鲁棒性就会比较高，利用拼接好的点云组建图，并在最后根据新拼接的点云组与全局地图匹配进行回环检测，把上述过程结合就是一个完整的二维激光的定位方案。本文SLAM系统全局流程如图1所示：

Figure 1. Global process

图1. 全局流程

2. 点云配准与拼接

激光雷达扫描得到初始数据不仅包含点云数据还有噪声点，需要经过处理才能使用，常见的点云预处理手段有直通滤波，体素滤波，统计滤波，半径滤波等 [10] [11] 。本文对点云数据的预处理采用体素滤波算法，它的原理是在二维平面上，通过划分小的栅格，用小栅格内的质心代替小栅格内的点云信息，从而简化栅格平面中的点云，使用此方法能够消除点云中的离散点和噪声。

体素滤波后的点云数据，需要通过点云配准算法求解相邻点云间的位姿。针对点云配准的算法也比较多，其中比较著名的有Besl提出的迭代最近点(Iterative Closest Point, ICP) [12] 算法，ICP算法利用最小二乘法，求得点与点之间最小的距离误差，该方法的优点是无需对位置进行初始估计，直接通过数学计算求解刚体变换；Fischler提出的随机样本一致性(RANSAC) [13] 方法，可以避免整个点云的迭代，从而显著提高算法效率，在二维和三维数据处理中得到了广泛应用；正态分布变换(NDT) [14] 方法用概率密度函数来确定两个点云间的最优的匹配，简化了特征匹配，因为不需要特征计算，所以配准时间较短。本文点云配准选择ICP算法，并对ICP算法的迭代环节经行改进。具体过程如下：设激光雷达采集得到的相邻两组数据点集为 $P_k$ 和 $P_{k+1}$ ，则相邻两帧点集之间的刚体变换为：

${P^{\prime }}_{k+1}=R{P}_{k+1}+T$ (1)

其中 $R=\left[\begin{array}{cc}\cos \Delta \phi & \sin \Delta \phi \\ -\sin \Delta \phi & \cos \Delta \phi \end{array}\right]$ 为 $P_k$ 和 $P_{k+1}$ 之间的旋转矩阵， $T=\left[\begin{array}{l}\Delta x\hfill \\ \Delta y\hfill \end{array}\right]$ 为 $P_k$ 和 $P_{k+1}$ 之间的平移向量。 $\Delta \phi$ 为 $P_k$

和 $P_{k+1}$ 之间的旋转角度， $\Delta x$ 为 $P_{k+1}$ 在x轴方向的位移， $\Delta y$ 为 $P_{k+1}$ 在y轴方向上的位移。

通过参数变换，将 $P_{k+1}$ 中的点集，转换到 $P_k$ 的坐标系下，实现点集匹配。在机器人连续运动采集的情况下，相邻两组激光点集中，实际只有部分点集能够重合，其余点需尽量做到距离最小，表示为：

$\min \left(\left|P_k-{P^{\prime }}_{k+1}\right|\right)$ (2)

此时激光点集匹配问题可以描述为求解R、T使得所表示的目标评价函数达到最小值：

$\min \left(g\left(R,T\right)\right)=\min \left(\frac{1}{n}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\left|P_k-R{P}_{k+1}-T\right|}^2}\right)$ (3)

目标评价函数求解过程如下：首先计算两组点云数据的中心点，分别表示为 ${\mu }^{P_k}$ 与 ${\mu }^{P_{k+1}}$ ，计算公式为：

$\{\begin{array}{l}{\mu }^{P_k}=\frac{1}{n}{\displaystyle \underset{i}{\overset{n}{\sum }}{a}_i},a_i\in P_k\hfill \\ {\mu }^{P_{k+1}}=\frac{1}{n}{\displaystyle \underset{i}{\overset{n}{\sum }}{b}_i},b_i\in P_{k+1}\hfill \end{array}$ (4)

其中 $\left\{a_i\right\}$ 为 $P_k$ 中的点集， $\left\{b_i\right\}$ 为 $P_{k+1}$ 中的点集，然后对 $P_k$ 和 $P_{k+1}$ 中的数据进行归一化处理：

$\{\begin{array}{l}{a^{\prime }}_i=a_i-{\mu }^{P_k}\hfill \\ {b^{\prime }}_i=b_i-{\mu }^{P_{k+1}}\hfill \end{array}$ (5)

得到新的目标函数：

$\begin{array}{c}g\left(R,T\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left|{a^{\prime }}_i-R{b^{\prime }}_i\right|}^2}\\ =\frac{1}{n}\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left|{a^{\prime }}_i\right|}^2}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left|R{b^{\prime }}_i\right|}^2}-2{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left|{a^{\prime }}_{i}R{b^{\prime }}_i\right|}^2}\right)\end{array}$ (6)

想要使目标函数最小，只需 $\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left|{a^{\prime }}_{i}R{b^{\prime }}_i\right|}^2}$ 最大，令：

$\mathrm{err}\left(\Delta \phi \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|{a^{\prime }}_{i}R{b^{\prime }}_i\right|}$ (7)

其中 $\Delta \phi$ 为两组点集之间的旋转角度，对式(7)中的 $\Delta \phi$ 求导：

$\frac{\partial err\left(\Delta \phi \right)}{\partial \Delta \phi }=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(\cos \Delta \phi \left(a_i^x{b}_i^y-a_i^y{b}_i^x\right)-\sin \Delta \phi \left(a_i^x{b}_i^x+a_i^y{b}_i^y\right)\right)}$ (8)

其中 $a_i^x$ ， $a_i^y$ ， $b_i^x$ ， $b_i^y$ 分别为 ${a^{\prime }}_i$ 和 ${b^{\prime }}_i$ 的x，y分量，进一步可得到：

$\frac{\sin \Delta \phi }{\cos \Delta \phi }=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(a_i^x{b}_i^y-a_i^y{b}_i^x\right)}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(a_i^x{b}_i^x+a_i^y{b}_i^y\right)}}$ (9)

即：

$\Delta \phi =\arctan \frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(a_i^x{b}_i^y-a_i^y{b}_i^x\right)}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(a_i^x{b}_i^x+a_i^y{b}_i^y\right)}}$ (10)

此时得到 $\Delta \phi$ ，就可以求得旋转矩阵R，经过参数变换后的两组点云数据中心重合，即 ${\mu }^{P_k}={\mu }^{{P^{\prime }}_{k+1}}$ 通过式(1)可得到平移向量T：

$T={\mu }^{P_k}-R{\mu }^{P_{k+1}}$ (11)

第一次得到的R、T如果直接使用，对应点对之间的距离可能不是最小，还需经过多次迭代才能得到最优解。为了减小迭代次数，提高算法效率，本文设计了一种迭代自适应终止策略，传统ICP算法每迭代一次目标点集与参考点集都会不断靠近，为了能够保证精度的同时不发生过度迭代的问题，本文利用平均绝对值误差(Mean Absolute Error, MAE)构建了一个迭代自适应终止策略，并将本文改进后的ICP算法命名为(Iterative adaptive ICP, IA-ICP)，具体过程为：通过计算第n次和第n − 1次对应点之间欧氏距离的MAE值，采用MAE的大小来描述第n次和第n − 1次恢复块内容的相似性，MAE值越小，表明两

次迭代内容越相似，进一步迭代带来的进步大不，本文设定当 ${\text{MAE}}_n/{\text{MAE}}_{n-1}\ge 0.95$ 时，停止迭代。其中MAE求解方式如式(12)所示：

$\mathrm{MAE}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|a_i-{b^{\prime }}_i\right|}$ (12)

其中 $\left\{a_i\right\}$ 为 $P_k$ 中的点集， $\left\{{b^{\prime }}_i\right\}$ 为 ${P^{\prime }}_{k+1}$ 中的点集，n为对应点数目。

求得最优R、T后，对相邻激光帧点云进行拼接，使得有效点云数目增多获得更多的环境信息，采用一种滑动窗口的策略，设滑动窗口大小为10，利用IA-ICP算法依次求出窗口内10帧数据相邻之间的位姿，并把窗口内帧数据转移到第一帧帧数据坐标系下，每更新一帧数据，删除最旧的一帧数据，并将剩余9帧点云数据转移到最新一帧点云数据的坐标下，每10帧作为一个拼接好的点云组。本文点云拼接算法流程如下：

<1> 系统开始运行，窗口内没有点云数据，此时将预处理后的待加入帧点云数据直接移入窗口内作为窗口内第1帧，如图2所示：

Figure 2. The system just started running

图2. 系统刚开始运行

然后利用IA-ICP算法，求出下一个待加入帧与窗口内第1帧之间的R、T，将该待加入帧移入窗口作为第1帧，窗口内原来的第1帧移动到第2帧位置，但实际过程中由于机器人快速转向等原因会导致丢帧，出现相邻两帧之间距离过大的问题，为解决这个问题，相邻帧之间建立距离约束，如果新的待加入帧与窗口内第1帧对应点云之间的距离满足约束条件，则将待加入帧移入窗口内，否则删除，具体过程为：设新的待加入帧点云的中心为 ${\mu }^{P_0}$ ，窗口内第一帧点云的中心为 ${\mu }^{P_1}$ ，两中心点之间的距离为：

$d=\frac{{\left[\mathrm{dist}\left(x_0,y_0\right)-\mathrm{dist}\left(x_1,y_1\right)\right]}^2}{{\left[\mathrm{dist}\left(x_0,y_0\right)+\mathrm{dist}\left(x_1,y_1\right)\right]}^2}\le {\delta }_1$ (13)

式中， ${\delta }_1$ 为设定的距离误差，若滑动窗口外待加入帧与窗口内第1帧距离误差满足式(13)，则将待加入帧移入滑动窗口内作为第1帧，原本窗口内的第1帧移到第2帧位置，再利用IA-ICP算法，求出下一个待加入帧与窗口内第1帧点云之间的R、T，依次对待加入帧利用式(13)进行判断直至滑动窗口内满10帧，如图3所示：

Figure 3.10 frames full in the window

图3.窗口内满10帧

当滑动窗口内满10帧时，将滑动窗口内第2帧至第10帧的数据的通过位姿变换转移到窗口内第1帧数据的坐标系下，拼接形成一个点云组：

$\{\begin{array}{l}\begin{array}{l}{P}_1=P_1\\ {P^{\prime }}_2=R_2{P}_2+T_2\end{array}\hfill \\ {P^{\prime }}_3=R_2\left(R_3{P}_3+T_3\right)+T_2\hfill \\ ⋮\hfill \\ {P^{\prime }}_{10}=R_2\left(R_3\left(\cdots \left(R_{10}{P}_{10}+T_{10}\right)\cdots \right)+T_3\right)+T_2\hfill \end{array}$ (13)

<2> 当滑动窗口内已有10帧数据，此时窗口内第10帧数据将作为待移除帧，当新的符合条件的待加入帧进入到窗口内，此时将窗口内第10帧移出窗口外作为废弃帧，窗口内其余帧依次右移形成新的点云组，如图4所示：

Figure 4. The system is running properly

图4.系统正常运行中

<3> 在系统运行过程中可能出现连续多帧待加入帧与滑动窗口内第一帧之间的约束都不满足式(13)，此时设定阈值k，如果连续k帧待加入帧与滑动窗口内第一帧之间的距离都不满足式(13)，则清空窗口内的点云，重新按照步骤<1>进行。

3. 实验分析

为验证本文算法的有效性，搭建移动机器人平台进行测试实验。机器人平台如图5所示，机器人底层由STM32控制四个麦克纳姆轮实现全向运动，并搭载Hokuyo激光雷达来获取机器人周围环境信息，上位机为工控机，其配置为Intel i7-1165G7，8GB内存，系统为Ubuntu18.04，ROS版本为Melodic。

Figure 5. Robot platform

图5. 机器人平台

实验检验分为三部分，一：传统ICP算法和IA-ICP算法对比；二：多种SLAM算法轨迹对比；三：多种SLAM算法建图精度对比。所有实验中机器人的角速度都为0.1 rad/s，线速度为0.2 m/s。

3.1. ICP算法迭代对比

在相同的条件下，对传统ICP算法和本文提出的IA-ICP算法进行比较，对比迭代次数，对比结果如图6所示，平均迭代次数与耗时对比如表1所示：

Table 1. Performance comparison

表1. 性能对比

Figure 6. Comparison of iterations

图6. 迭代次数对比

由图6可以明显的看出，本文IA-ICP算法比传统ICP算法完成迭代所用的次数更少，迭代曲线收敛的更快，由表1可知IA-ICP算法比较传统ICP算法迭代次数平均减少50.22%；迭代次数减少，会伴随着算法运行时间减少，IA-ICP算法在运行时间上，相比于传统ICP算法减小39.67%，因此IA-ICP算法有更高的效率。

3.2. 轨迹对比：

实验环境为教学楼内走廊，如图7所示，具有地面平坦，行人少等优点，适合移动机器人测试,机器人运动路径如图中蓝色箭头所示：

Figure 7. Experimental environment

图7. 实验环境

在图7所示实验场景中，分别使用改进前的方式与改进后的方式，以及Gmapping算法进行实验和文献 [15] 中的方法，每种算法分别按图7中蓝色路径运行5次，并对5次SLAM轨求平均值，得到图8中的轨迹曲线。

Figure 8. Trajectory comparison

图8. 轨迹对比

从图8轨迹曲线可以看出，本文所提出的方法最接近真实路径，其次文献 [15] 中的方法，然后是Gmapping算法，与偏离真实轨迹最大的是本文未改进前的算法。由此说明通过滑动窗口拼接能够很好的估计机器人的位姿，滑动窗口拼接的点云组在前期建图提供了良好的精度，同时又有利于后期回环检测，使得机器人运动轨迹与实际轨迹偏差不大，有效减小了单线激光误匹配情况。三种算法在运行过程中在x轴、y轴的平均位移偏差如表2所示：

Table 2. Mean displacement deviation

表2. 平均位移偏差

从表2的数据可以看出，本文改进后的算法，误差更小，精度更高，在x轴方向上，本文改进后的方法相比Gmapping算法的轨迹精度提高48.39%，相比文献 [15] 中的算法轨迹精度提高42.86%，相比本文未改进前的算法的轨迹精度提高61.90%；在y轴方向上，本文改进后的方法相比Gmapping算法的轨迹精度提高53.57%，相比文献 [15] 中的算法轨迹精度提高50.00%，相比本文未改进前的算法的轨迹精度提高62.86%。

3.3. 建图对比

在图7所示的实验场景中，使用本文改进前的算法、本文改进后的算法，以及Gmapping算法，构建地图结果如图9所示。

由表3可以看出，本文改进后的算法相对于Gmapping算法构建的整体地图最大误差减小43.75%，平均误差减小19.23%，匹配耗时减小28.57%；相对与本文为改进前的算法构建的整体地图最大误差减小61.70%，平均误差减小43.24%，匹配耗时减小36.62%。最终本文算法的准确率达到95.4%，相比于Gmapping算法的90.10%和本文算法未改进前的86.71%都有了较大的提升。

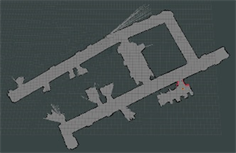
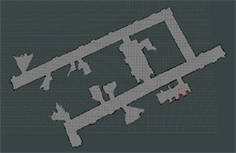
本文改进前 本文改进后 Gmapping

Figure 9. Drawing comparison

图9. 建图对比

Table 3. Performance comparison of SLAM algorithms

表3. SLAM算法性能对比

4. 结论

本文针对传统单线激光SLAM由于单帧点云数据量过少，在某些局部相似的场景中可能出现得分很高的误匹配情况，提出了一种基于滑动窗口的点云拼接算法，并对传统点云配准算法进行改进，提出一种迭代自适应终止的ICP算法提高了点云配准的速度。先利用迭代自适应终止ICP算法求出点云间的位姿，然后通过滑动窗口拼接形成一个局部地图，利用局部地图进行地图构建和回环检测，经过实验验证，本文所提出的方法在室内低速环境下能够准确实现室内定位与地图构建，具有良好的实用价值。

NOTES

^*通讯作者。