基于ElGamal的改进最低有效位信息隐藏算法设计

ElGamal-Based Improved Least Significant Bit Information Hiding Algorithm Design

摘要: 当前网络环境下，数据安全与隐私威胁日趋多样化和复杂化，单一使用信息隐藏技术或者图像加密技术进行信息的传输，已经无法满足安全可靠传输的要求，提出了一种信息隐藏和图像加密相结合的方法，对数据进行了双层保护。第一层利用改进最低有效位信息隐藏算法将秘密信息嵌入至载体图像中，第二层利用ElGamal加密算法对载体图像进行加密。通过实验证明，该方法能够准确提取秘密信息，可实行性高，在提高数据嵌入量的同时，为数据提供了更高级别的安全性。

Abstract: In the current network environment, data security and privacy threats are becoming increasingly diverse and complex. So the single use of information hiding technology or image encryption technology for information transmission can no longer meet the requirements of safe and reliable transmission, and a method combining information hiding and image encryption is proposed to protect the data in two layers. The first layer uses the improved least significant bit information hiding algorithm to embed the secret information into the carrier image, and the second layer uses the ElGamal encryption algorithm to encrypt the carrier image. Through experiments, it is proved that the method can accurately extract secret information with high implementability and provide a higher level of security for the data while improving the data embedding volume.

1. 引言

新型网络环境尤其是云计算和群智感知环境下数据安全与隐私威胁日趋多样化、复杂化和规模化，对传统信息安全保护技术带来了巨大冲击和严峻挑战。人们在日常生活当中无时无刻不在进行数据的传递、信息的交换，这也使得一些非法分子有机可乘，通过窃取他人信息进行非法牟利。因此，信息的安全传输已然成为当今社会人们的重要课题。

密码学是研究如何隐密地传递信息的学科，在现代特别指对信息以及其传输的数学性研究，常被认为是数学和计算机科学的分支，和信息论也密切相关。信息隐藏的使用从远古时代就开始了，以限制未经授权的干预对机密内容的检测的方式来交换秘密信息 [1] 。信息隐藏技术发展的历史表明，各种方法如隐形墨水、微点、密码术、哈希、隐写术等被引入到载体介质中，以隐藏秘密信息，减少与安全相关的问题 [1] [2] 。随着数字化时代的发展，人们慢慢发现，单纯的使用密码学技术或者信息隐藏技术进行信息的传输，已经无法满足安全可靠传输的要求，所以有学者开始提出将两者进行结合的方式，即密码学结合信息隐藏，来实现更高可能的安全性。简单来说，在发送方发送秘密数据之前，先将密文数据嵌入到载体之中，再对载体进行加密，通过两者结合的方式，使得数据的保密性大大增强，提高了数据在传输过程中的安全性。

加密图像信息隐藏是将图像加密和信息隐藏结合使用的一种技术 [3] [4] [5] [6] [7] ，发送方使用该技术进行信息的发送，接收方在收到信息之后，需要先对载体图像进行解密，才能提取秘密信息，一定程度上为秘密信息提供了双层保护，提供了更好的安全性 [8] 。

基于上述情况，本文提出了一种基于信息隐藏和图像加密相结合的方法，对原始待传输的数据以二进制数据流形式通过改进最低有效位的方法嵌入到载体图像中，采用ElGamal加密算法对载体图像进行数据加密，将加密后的数据作为信息进行传输，通过将两者结合的方式提升了数据传输的安全性。

2. 预备知识

2.1. 阶

设n > 1，a和n互质，则必有一个x (1 ≤ x ≤ n-1)使得：a^x ≡ 1 (mod n)，满足a^x ≡ 1 (mod n)的最小整数x，称为a模n的阶。观察方程a^x ≡ 1 (mod n)，根据欧拉定理，若Φ (n)是方程的一个解，且Φ (n)是a模n的阶时，称a为n的一个本原元。

2.2. 本原元

当a模n的阶为Φ (n)，当且仅当x是Φ (n)的倍数，使得a^x ≡ 1 (mod n)成立，此时称a为n的本原元。

2.3. 离散对数问题

设p是素数，g是p的本原元，即g⁰，g¹，g²，...，g^{p − 2} 在mod p下产生1到p − 1的所有值，所以对任意y є [1，...，p − 1]有唯一的x є [0，...，p − 2]使得y ≡ g^x(mod p)，称x为模p下以g为底y的离散对数，即为x ≡ log_gy (mod p − 1)。

当g，p，x已知时，求y比较容易，但如果已知g，p，y且p很大，求x则非常困难。

2.4. EIgamal密码系统

ElGamal加密算法是由 Tather ElGamal (塔希尔·盖莫尔)在1985年提出的一个基于迪菲–赫尔曼密钥(D-H)交换的非对称加密算法。它是一种基于离散对数难题的加密体系，与RSA算法一样，都能用于数据加密和数据签名。但是两者的原理不一样，ElGamal算法基于离散对数问题，而RSA算法基于大素数分解困难问题。

与RSA算法相比，ElGamal算法的特点就是，哪怕是使用相同的私钥，对相同的明文进行加密，每次加密后得到的签名也各不相同，有效的防止了网络中可能出现的重放攻击，因此，ELGamal算法得到了广泛的应用 [9] [10] 。

2.4.1. 参数定义和密钥生成

1) 随机选择一个大素数p，且要求p − 1有大素数因子。再选择一个模p的本原元g，将p和g公开；

2) 随机选择一个整数x作为密钥，2 ≤ x ≤ p − 2；

3) 计算y= g^x mod p，取y为公钥。

2.4.2. 加密算法

1) 将M编码为一个在0到p − 1之间的整数m作为传输的明文；

2) 随机地选取一个整数r，2 ≤ r ≤ p − 2；

3) C1 = g^r mod p，C2 = m × y^r mod p；

4) 密文为(C1, C2)。

2.4.3. 解密算法

由密文可得明文M，M = C2 × C1^(−x) mod p。

3. 图像加密

3.1. 图像加密概述

数字图像比声音、文字等蕴涵更多的信息量，在多媒体信息中也占有举足轻重的地位。因此，对图像信息处理是信息保密通信中重要的部分。数字图像加密就是在发送端采用一定的算法，如ECC，RSA等加密算法作用于一幅待传输的图像明文，在密钥控制下使其变成不可识别的密文，达到图像保密的目的。解密时，在接收端采用相应的算法解密，恢复出原文。一个完整的图像加解密流程应该如图1所示。

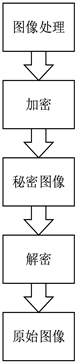
Figure 1. Digital image encryption and decryption flowchart

图1. 数字图像加解密流程图

3.2. 最低有效位(LSB)数字水印算法

LSB (Least Significant Bit)数字水印算法是一种常用的数字图像水印技术，用于在数字图像中嵌入隐藏信息，以实现版权保护、身份验证或数据完整性验证等目的。该算法利用数字图像像素中的最低有效位(Least Significant Bit)来嵌入水印信息，因此被称为LSB数字水印算法。

LSB数字水印算法的基本思想是将待嵌入的水印信息的二进制比特序列插入到数字图像像素的最低有效位中，从而实现信息的隐藏。最低有效位是指二进制数中的最右边一位，其对图像的视觉影响较小，不容易被察觉到 [11] [12] 。

3.3. 改进最低有效位(LSB)数字水印算法

传统的LSB数字水印算法，通过每个像素的最低位隐藏1比特的秘密信息，信息被嵌入到数字媒体中的最低有效位中，对于人眼或耳朵来说，这些变化通常是微不可见或听不出来的。

该算法通常是将待嵌入图像的像素值，转化为二进制比特流，即将每一位像素值表示成为8位二进制比特流，在此基础上通过修改8位中的最低位，来嵌入秘密信息。我们观察到，对于载体图像，一个像素值的最低两位，即最低位和次低位两位，穷举其组合位00，01，11，10。除此之外最低两位不会再有其他组合。我们考虑到嵌入信息，同样也可将其转化为二进制比特流，考虑两两组合的形式，其组合同样为00，01，11，10。以此推理，当我们需要将秘密信息嵌入到载体图像当中时，以此规律可进行更高效的信息嵌入。此处我们假设秘密信息的两两组合为(a, b)，具体方法可分四种情况进行讨论，即(a, b)可以表示(0, 0)、(0, 1)、(1, 1)、(1, 0)四种情况进行讨论。

1、当嵌入信息(a, b)为(0, 0)组合时，载体像素值最低两位为(0, 0)或者(0, 1)情况时，不需修改(像素值为(0, 0))或者仅修改最低位数据(像素值为(0, 1))即可完成信息的嵌入。

2、当嵌入信息(a, b)为(0, 1)组合时，载体像素值最低两位为(0, 0)或者(0, 1)情况时，不需修改(像素值为(0, 1))或者仅修改最低位数据(像素值为(0, 0))即可完成信息的嵌入。

3、当嵌入信息(a, b)为(1, 0)组合时，载体像素值最低两位为(1, 0)或者(1, 1)情况时，不需修改(像素值为(1, 0))或者仅修改最低位数据(像素值为(1, 1))即可完成信息的嵌入。

4、当嵌入信息(a, b)为(1, 1)组合时，载体像素值最低两位为(1, 0)或者(1, 1)情况时，不需修改(像素值为(1, 1))或者仅修改最低位数据(像素值为(1, 0))即可完成信息的嵌入。

以上我们考虑了四种特殊的组合情况，在对像素值最低两位至多修改一位的情况下即可嵌入两位秘密信息。但当(a, b)为(1, 1)或者(1, 0)的组合，遇到像素最低两位(0, 1)和(0, 0)的组合的时候，无法通过修改一位或是不修改位进行数据的嵌入，当(a, b)为(0, 0)或者(0, 1)的组合，遇到像素值最低两位为(1, 1)和(1, 0)，同样也无法通过仅修改最低位信息位来完成信息的嵌入，此时，我们通过引进标识位，来实现修改最低位来隐藏两位数据。具体逻辑如下：

当我们嵌入秘密信息的首位和载体图像像素值的次低位相同时，即上文我们考虑到的四种情况，我们可将标识位置为0。当我们嵌入秘密信息的首位和载体图像像素值的次低位不同时，我们可将标识为置为1。即当(a, b)为(1, 1)或者(1, 0)的组合，遇到像素最低两位(0, 1)和(0, 0)的组合时和当(a, b)为(0, 0)或者(0, 1)的组合，遇到像素值最低两位为(1, 1)和(1, 0)时。

改进的LSB数字水印算法，以一定的嵌入规则，可实现修改一个最低有效位，嵌入两位数据，实现了从4个像素嵌入4比特信息，到4个像素嵌入8比特信息的转变，极大提升了原始LSB嵌入算法的容量，且因为只修改了最低有效位，可实现同原本LSB数字水印一样的隐蔽性。

4. EIGamal加密隐藏算法

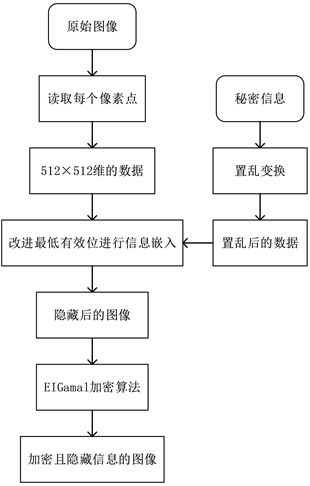
Figure 2. Image encryption and information embedding flowchart

图2. 图像加密及信息嵌入流程图

本文所提出的算法是基于非对称密码体制来实现图像加密，系统隐藏和加密主要流程如图2所示，图3为解密以及信息提取的主要流程，隐藏与加密的具体步骤如下：

(1) 发送方读取待隐藏的秘密信息；

(2) 在信息隐藏之前，对图像信息进行预处理，具体算法参考4.1部分；

(3) 读取载体图像的各位上的像素值；

(4) 将载体图像十进制像素值转化为二进制比特流，提取各个像素值的次低位和最低位；

(5) 将秘密信息进行两两分组，进行信息嵌入，具体算法参考3.3部分；

(6) 将嵌入秘密信息的载体图像的每一位十进制像素值，作为明文进行 EIGamal 加密，具体算法参考4.2部分；

(7) 将经过EIGamal加密后的像素值重新填充至各个位置。

与上述过程相似，图像解密与信息提取的主要步骤如下：

(1) 接收端接收到嵌入秘密信息的加密的载体图像；

(2) 对载体图像的每一像素值进行EIGamal解密，具体算法参照4.2部分；

(3) 根据标识位进行秘密信息的提取；

(4) 对解密出来的秘密信息进行逆置乱操作。

经过上述步骤。可实现载体图像的加解密以及秘密信息的隐藏和提取。

4.1. 信息隐藏

Figure 3. Image decryption and information extraction flowchart

图3. 图像解密及信息提取流程图

在隐藏信息之前，算法对秘密信息进行了预处理操作，保证了更高的安全性。这里采用最经典的Arnold置换，置换过程可用式(1)表示：

$\left[\begin{array}{l}{x}_{n+1}\\ y_{n+1}\end{array}\right]=\left(\begin{array}{cc}1& b\\ a& ab+1\end{array}\right)\left[\begin{array}{l}{x}_n\\ y_n\end{array}\right]\mathrm{mod}\left(N\right)$ (1)

其中x，y表示变换前灰度图中像素的位置，x_n+1，y_n+1表示变换之后的像素位置，a，b为参数，n表示当前变换的次数，N为图像的长或宽(由于该算法只适用于长宽相等的图像，所以我们不讨论M不等于N的情况)，mod为模运算。

经过Arnold变换之后图像的像素位置会重新排列，这样图像会显得杂乱无章，从而实现了对图像的置乱加密效果。接着进行下一步隐藏操作，隐藏算法利用的是改进最低有效位算法，具体可参考3.3部分。在对信息进行嵌入的同时，我们选择在载体图像的奇数列进行信息的嵌入，这样能保证嵌入次序的不规则性，且对图像的影响会更小。

经过如上步骤，完成了秘密信息的隐藏，发送方将经过信息嵌入的图像进行EIGamal加密后发给接收端，发送端的工作就全部结束，但整体工作并未停止，接收端收到发送端发来的消息时，需要进行图像的解密和秘密信息的提取工作。在已知标识位即对应规则的前提下，可进行秘密图像的提取，提取之后进行EIGamal解密便可恢复原始秘密信息。

4.2. 图像加解密

采用EIGamal加密算法进行图像加密时，根据EIGamal算法的原理，需要将图像的十进制数作为明文数据。算法加密过程如下：

(1) 选择一个大素数p，且要求p − 1有大素数因子。再选择一个模p的本原元g。将p和g公开；

(2) 随机选择一个整数x作为密钥，2 ≤ x ≤ p-2；

(3) 计算y = g^x mod p，取y为公钥；

(4) 将明文数据编码为一个在0到p − 1之间的整数m作为传输的明文；

(5) 随机地选取一个整数r，2 ≤ r ≤ p − 2；

(6) 经过加密后，发送方将生成C1，C2；

(7) 发送方将C1发送给接收方，将C2填充至原始图像各个位置。

至此，就完成了图像信息的加密过程。解密过程采用EIGamal解密算法进行图像解密时，通过将图像的每一像素值作为密文输入，即可解得明文。过程如下：

(1) 接收方读取加密图像每一位置上的像素值；

(2) 将像素值赋给C2；

(3) 由M = C2 × C1^(−x) mod p，即可解得实际明文数据；

(4) 将明文数据填充回各像素；

(5) 图像完成解密。

5. 实验结果与分析

本文通过大量的实验验证，所提出的算法均取得了良好的效果，在完成信息隐藏和图像加密的基础上，对于秘密信息能够进行精准无误的提取。实验部分仅以Cameraman、Goldhill、Lena、Peppers四幅大小位512 × 512的灰度图像进行结果说明，具体图像如图4所示。秘密信息图像如图5所示。所有实验均在MatlabR2017b系统平台进行仿真实现。

图4. 载体图像

Figure 5. Secret infographic

图5. 秘密信息图

5.1. 算法有效性验证

具体实验情况如图所示，利用本文的隐藏算法对图4的秘密信息进行信息嵌入得到的图像如图6(a)~(d)所示。图7中的四幅图像分别表示的是在载体图像中隐藏秘密信息之后进行加密的结果图，图8和图9的(a)~(d)分别对应的是解密图像和提取的秘密信息。

图6. 水印嵌入

图7. 加密图像

图8. 解密图像

图9. 提取水印

5.2. 统计结果及性能分析

(1) 正确性

该算法的正确性包括加密图像的正确解密及水印信息的正确提取。从上述实验结果上我们可以发现，对于解密出来的图像和提取出来的水印信息，均能做到准确无误。为了更好的对结果进行说明，我们采用归一化相关系数NC，对结果进行说明，NC的计算公式如下：

$NC=\frac{{\displaystyle \underset{i=1}{\overset{M}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{W}_{i,j}\times W^{\text{'}}{}_{i,j}}}}{{\displaystyle \underset{i=1}{\overset{M}{\sum }}{\displaystyle \underset{j=1}{\overset{N}{\sum }}{(W_{i,j})}^2}}}$ (2)

其中W_i,j和W^’_i,j和分别是原始秘密信息和提取的秘密信息对应位置上的像素值。其数值意义为两者越接近，则数值越接近1。同时根据表1计算的结果，可知该算法能够完全恢复秘密信息即精准提取秘密信息。

Table 1. The effect performance index of secret information extraction

表1. 秘密信息提取的效果性能指数

(2) 嵌入容量对比

对于传统最低有效位(LSB)算法，一个像素值仅仅嵌入一比特数据，对于本文所提出的改进最低有效位(LSB)算法，一个像素通过对比标识为能够完成两位秘密信息的嵌入，对于一副大小为512 × 512大小的秘密图像，选用不同的方法所需载体图像大小不同，具体对比结果如表2所示。

Table 2. Embedded capacity information comparison (bits)

表2. 嵌入容量信息对比(比特)

此外，我们还对算法的其他性能进行了评估分析。透明性表示秘密信息在载体图像中的可见程度，因此对隐藏信息后的图像进行了PSNR值的计算，对于一幅大小为M × N的图像，其计算公式为：

$\text{PSNR}=10\times \lg \left(\frac{{\text{MaxValue}}^2}{\text{MSE}}\right)$ (3)

其中MSE代表的是原始图像与隐藏信息后图像的均方差，它可以直接反映出图像嵌入秘密信息前后对原始载体图像像素的修改量大小，考察的是图像嵌入信息前后之间的差异性，它的计算公式为

$\text{MSE}=\frac{1}{MN}{\displaystyle {\sum }_{x-1}^M{\displaystyle {\sum }_{y-1}^N\left[I\left(x,y\right)-I_M\left(x,y\right)\right]}}$ (4)

公式中I (x, y)代表秘密信息嵌入之前，坐标为(x, y)的像素值，I_M (x, y)代表秘密信息嵌入以后，坐标为(x, y)的像素值。MAXValue代表信号的最大值。对于8位的灰度图像来说，MaxValue的最大值为255。PSNR的数值意义表示为含秘图像与原始图像之间的差异，其值越大，代表图像失真度越小。也从另一个角度反映了秘密信息的隐藏程度。表3所示的是对同样大小的载体图像采用不同算法进行加密之后计算的PSNR值的对比，从表中我们可以看出本文算法相较于其他两种，PSNR值更高，代表效果优于其他两种算法。

Table 3. Comparison of PSNR values

表3. PSNR值对比

(3) 安全性分析

ElGamal加密算法的安全性主要基于离散对数问题的困难性。在ElGamal加密过程中，图像的每个像素都被视为一个整数，并将其作为明文进行加密。加密过程涉及生成公钥和私钥、选择大素数和生成生成元等步骤，其中离散对数问题的难解性是确保加密安全性的基础。对于每个像素的加密，ElGamal算法涉及到多次离散指数运算，包括求幂和取模运算。这些运算使得破解者难以通过观察加密后的像素值来推导出原始的像素值。加密后的像素值是通过加密密钥(公钥)和随机数生成的，而这些参数与图像内容无关，增加了破解的难度。与文献14 [14] 所实现方法进行了相关的对比，如表4所示，验证了本文算法具有更高的安全性。

Table 4. Security comparison

表4. 安全性对比

6. 结语

针对当前网络环境下，单一使用信息隐藏或者图像加密技术无法满足可靠传输要求的问题，提出了一种新的方案，结合了信息隐藏和图像加密技术，以增强算法的安全性。该算法使用改进的最低有效位算法进行信息隐藏，根据每个像素最低两位的对应关系进行信息嵌入，改进后的算法可通过1像素嵌入2比特数据，与原有的1像素嵌入1比特数据相比，提高了嵌入容量，实现了嵌入的最优化，且由于只修改了最低位的数据，对载体图像的影响相对较小，在不破坏载体图像的前提下保证了秘密信息的不可见性。此外，使用EIGamal加解密算法对图像进行加密，在加密过程中，图像的每个像素经过加密算法的转换，使得未经授权的用户无法获得有关原始图像的任何有用信息。解密时，只有使用正确的私钥才能还原出原始的图像数据。该算法基于离散对数问题，为图像数据提供了更高级别的安全性。通过结合信息隐藏和图像加密技术，能够在传输过程中确保秘密信息的安全性和完整性，从而满足可靠传输的要求。

通过相关的实验验证，证明了该算法的可行性。但仍存在一些不足，例如当受到一些几何、滤波攻击时，对秘密信息会有一定的影响，因此，未来的工作需要进一步解决这些问题。

基金项目

国家自然科学基金(61370188)；北京市教委科学研究计划项目(KM202010015009, KM202110015004, KM202310015002)；北京印刷学院博士启动金项目(27170120003/020)；北京印刷学院科研创新团队项目(Eb202101)；北京印刷学院博士启动金项目(27170122006)；北京市高等教育学会2022年立项面上课题(MS2022093)；北京印刷学院网络空间安全培育学科建设项目(21090123010)；北京印刷学院校级在线课程建设项目(《信息隐藏与数字水印》)。