协作机器人结构设计及齿轮传动系统仿真

Structural Design and Gear Transmission System Simulation of Collaborative Robots

摘要: 本文针对看守所传统送餐方式存在安全性差、效率低的问题，研制了一款实现特种场所无人化送餐的协作式机器人，并对其关键传动系统进行有限元分析。结合Solidworks软件设计了整机三维模型，采用模态分析与瞬态动力学仿真分析相结合的手段，研究了机械臂旋转模块中的齿轮传动系统非线性动力学特性。仿真结果显示：齿轮系统的前8阶固有频率远高于共振频率，在不同扭矩输入下，最大变形量为1.729 mm，最大应力值为723.1 Pa。基于赫兹理论得到齿轮接触面疲劳强度极限为6.3258 Mpa，低于材料屈服强度。与有限元分析结果进行对比，验证装置在强度、刚度以及动态响应方面均符合工程设计要求，为后续研发和优化提供了理论依据。目前对样机已完成调试，结果良好，具有广阔的应用前景。

Abstract: In this study, a collaborative robot was developed to address the safety and efficiency issues in tra-ditional prison meal delivery. The key transmission system of the robot was analyzed using finite element analysis, and the entire machine was designed using Solidworks software. A combination of modal analysis and transient dynamic simulation analysis was used to investigate the nonlinear dynamic characteristics of the gear transmission system in the rotational module of the robotic arm. The results showed that the first eight orders of the gear system’s natural frequency were far higher than the resonance frequency, with a maximum deformation of 1.729 mm and a maximum stress value of 723.1 Pa under different torque inputs. Based on the Hertz theory, the fatigue strength limit of the gear contact surface was obtained to be 6.3258 MPa, which is lower than the material yield strength. Compared with the finite element analysis results, the device meets the engineering design requirements in terms of strength, stiffness, and dynamic response, providing a theoretical basis for future research and optimization. The prototype has been successfully debugged, and the results are promising, with broad application prospects.

1. 引言

随着人工智能的不断发展以及机器人技术在各领域的拓展应用 [1] ，人们设计了集机械臂抓取、视觉识别、自动导向车(Automated Guided Vehicle, AGV)、拖动示教等功能于一体的协作机器人，它能胜任单一机器人无法承担的复杂任务。协作机器人具备广阔的应用前景，彭可 [2] 等结合机械臂抓取与放置物料的能力以及AGV在规定路径上行驶的功能，建立了一套仓储分拣系统，使仓储物流进一步实现智能化；秦俊飞 [3] 等基于机械臂、视觉检测技术、AGV，设计出一款智能化焊接机器人，提高整体工作效率，其成果也在标准化机房中得到实践检验；吕开旺 [4] 等借助机械臂、AGV、相机等硬件条件，研究了一种视觉引导协作机器人上下料系统，并验证该系统的工作精度与增益效果，提供工程项目参考价值；范瑞鹏等 [5] 提出一种AGV协作机器人设计方案，该方案包括规划复杂路径、机械臂装卸，为实现全自动AGV提供参考；温秀兰 [6] 等设计了一款具备多种功能的教学机器人，能进行拖动示教、视觉引导、在线编程、协作抓取、运动学分析等实验，较好满足了智能制造教学要求。

研发协作机器人并非简单的功能堆叠，而是各模块有机结合实现更优异的效果，最普遍运用的案例便是机械臂、AGV、视觉系统的配合使用，该组合将机器人本体作为载体，模拟实现了人类手、眼、脚功能，而只有兼备可靠性与耐久度的机构才能持续精准地作业，故有必要对于整机或是关键结构进行有限元校核。傅旻 [7] 等针对冲压机器人工作中执行机构与挡块会经常性发生碰撞的问题，利用Abaqus进行碰撞仿真分析，根据结果对结构与零部件选型进行优化，既节约研发成本，也大大提升冲压生产的效率；公续银 [8] 等设计了一种机器人的升降装置，利用ANSYS软件对其螺旋传动机构的关键连接部位进行应力分析与模态分析，验证了设计方案的合理性；徐金章和王延飞 [9] 对码垛机器人传动结构中的齿轮轴进行仿真分析，旨在观测传递扭矩时齿轮的受力情况，便于后续部件改良工作；Wang [10] 等综合分析RV减速器、输出轴和齿轮传动系统的模态振型，确定各阶频率的分布以及部件的应力应变情况，便于后续机械臂关节优化工作。

上述研究主要是针对机器人主体结构或作业频繁位置处的可靠性以及受力分析，鲜有学者对于机器人关节处传动系统进行研究。齿轮传动是由齿轮副传递运动和动力的装置，由于是依靠本身的结构尺寸和材料强度来承受外界载荷，因齿轮轴弯曲变形产生的轴向力、齿轮副啮合力等激励力会引发系统的共振，而被激起的异常应力应变相互传递，影响其他关节的性能，这便对传动系统齿轮材料的使用经济性、安全性、材料自身强度提出相应要求，故对于齿轮的强度校核和材料匹配验证是十分必要的。

2. 送餐机器人整机结构设计

2.1. 机器人外观结构

本文将研究一款协作式机器人，旨在实现监管场所无人化送餐。整机外部结构主要有机器人本体、人机交互控制板、底部AGV载具、机械臂单元、视觉感知系统等几个部分组成，本章将重点介绍机器人的外部结构设计及机械臂单元。

机器人本体是一个箱体结构，外壳采用普通碳钢，内部加强筋采用不锈钢，兼备内固支撑与优秀的承重能力，内部能容纳机械臂单元，设计了存放餐框的隔层；底部AGV载具根据地标二维码，将协作机器人运载至指定位置；视觉感知系统装载于机械臂末端夹取装置中，识别待搬运餐框的距离与姿态；机械臂单元是协作机器人的末端执行机构，内嵌于机器人本体中，该单元主要由升降模组、上伸出臂移动模组、旋转模组、下抱臂移动模组、末端夹取装置以及各运动模组机械臂载体、控制系统、传动系统等组成，控制板通过485总线通讯，向各运动关节伺服电机发送规定数量、频率的脉冲信号。

以下介绍两种工况，便于直观了解机器人运行原理。工况1：上伸出臂伸出一段距离，从而将机械臂单元带离箱体，接着升降模组将机械臂单元移动至指定高度。工况2：基于工况1，旋转模组开始工作，使下抱臂模组与待取餐框平行，随后下抱臂伸出一段距离，末端夹持装置等待MCU夹取指令。

所设计的整机实体模型以及所描述工况如图1所示。

(a) 工况1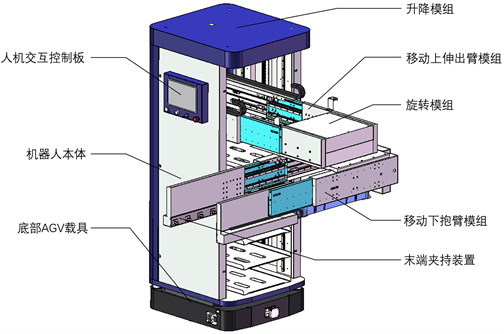(b) 工况2

Figure 1. Food delivery robot physical model

图1. 送餐机器人实体模型

2.2. 机械臂单元

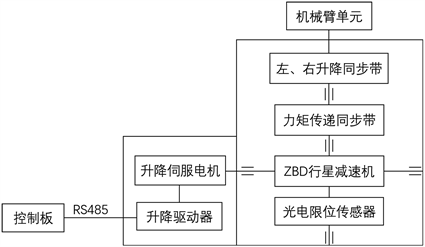
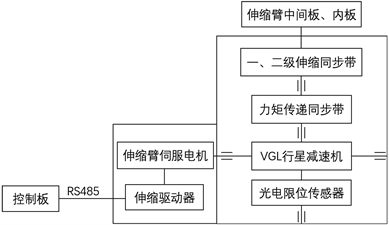
机械臂作为协作机器人的主要执行机构，按照工况运动顺序共有五个自由度，分别是上伸出臂移动关节、升降关节、旋转关节、下抱臂移动关节、末端夹取装置移动关节。各关节伺服电机驱动源经过减速装置、联轴器、执行机构等，将电机的旋转运动转化为直线位移、齿轮或齿条啮合传动。

2.2.1. 机械臂关节运动方案设计

机械臂单元共有五个运动单元模组，分别是升降模组、两级伸缩臂模组、旋转模组、末端夹持装置。针对机器人的运动范围、关节结构、关节之间的协调关系、控制系统等设计要求，绘制机械臂各模组运动方案简图，如图2所示。

(a) 升降关节

(b) 伸缩臂关节

(c) 旋转关节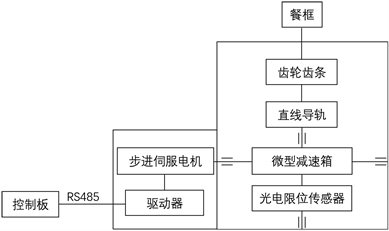(d) 末端执行器关节

Figure 2. Sketch of the motion scheme of each module of the robot

图2. 机器人各模组运动方案简图

2.2.2. 关节输出扭矩计算

电机输出扭矩与电机运行转速成反比，与电机功率成正比。在伺服电机输出端安装减速器装置实现降速增矩的效果，电机理论输出扭矩计算公式及经过减速装置后的实际输出扭矩计算公式如下：

$T_d=9550\times \frac{P}{n}$ (1)

$T_s=T_d\times i$ (2)

式中： $T_d$ 为电机额定输出扭矩， $P$ 为电机输出功率， $n$ 为电机转速， $i$ 代表减速器减速比， $T_s$ 为系统实际输出扭矩。当电机以不同的转速运行时，各个关节扭矩输出以及相关参数如表1所示：

Table 1. Calculated torque parameters for each joint

表1. 各关节扭矩计算参数

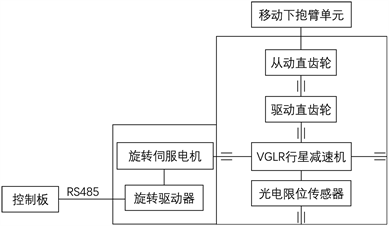
2.3. 旋转关节输出扭矩分析

由表1可得各关节额定输出扭矩最大处为旋转模组，此处负载转矩最大，于是本文将重点分析机械臂旋转模组中的直齿轮传动系统。通过经验与调研，确定旋转模组驱动源为60LCB040C伺服电机-VGLR系列行星减速器。不考虑传动系统能量耗损，在不同的电机转速下，输出扭矩如表2所示：

Table 2. Rotary joint motor torque calculation parameters

表2. 旋转关节电机扭矩计算参数

该齿轮传动系统中的从动轮与驱动轮齿数分别是25、85，通过固定在电机轴上的驱动齿轮轴传递扭矩至从动齿轮，直齿轮系统啮合实现机械臂单元后半部分的旋转，并对其进行有限元分析，验证设计方案可行性。在软件中对其进行建模，并组装成正切啮合的齿轮装配体，其三维实体模型如图3所示。

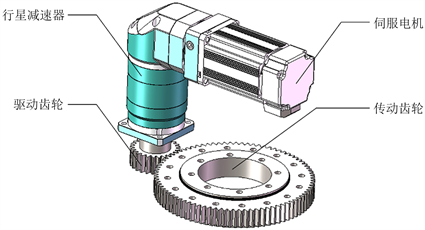
Figure 3. Gear train assembly drawing

图3. 齿轮传动系统装配图

3. 齿轮系统的仿真分析

3.1. 有限元基本理论

有限元分析(Finite Element Analysis, FEA)是面向结构力学分析的一种数值计算方法，常见的有限元分析软件包括但不限于Abaqus、Ansys、Hypermesh、COMSOL，用于求解各种工程和物理问题。一般分析流程概括为以下六步：结构离散化、定义材料、连接设置、定义边界条件、求解计算、结果后处理。图4是Abaqus有限元分析流程图，为本文及相关仿真研究提供参考。

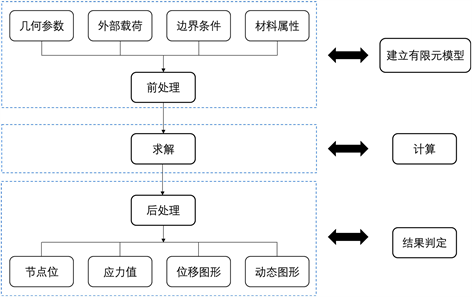
Figure 4. Finite element analysis process

图4. 有限元分析流程

3.2. 齿轮系统模态仿真分析

该旋转关节齿轮系统在工作中，由于输入扭矩的变化与齿轮副啮合作用会受到周期性冲击载荷，所引发的系统振动高频分量即齿轮的固有振动频率。模态分析可以确定设计结构或机器零件各阶振动特性及其所属频率范围，作为承受动态载荷结构设计中的重要参数，能直观体现结构关键位置的变形趋势，本文选取齿轮系统进行模态分析，便于设计后续优化方案，防止两齿啮合过程中发生共振现象。

3.2.1. 齿轮啮合有限元模型

有限元软件与三维制图软件具备良好的数据互通性，为降低模型的复杂程度且还原其结构特征，通过建模软件Solidworks删除模型轴孔特征及电机、减速器部件，简化后的齿轮传动系统如图5所示。

Figure 5. Simplified model of a gear system

图5. 齿轮系统简化模型

3.2.2. 模态仿真前处理

依照前文的有限元分析流程图，对简化后的有限元模型进行前处理。定义驱动轮与从动轮部件的材料属性，前者为45钢，屈服强度为355 MPa，密度为7850 kg/m³，泊松比为0.29，弹性模量为206 GPa；后者为冷拔处理后的碳素钢，屈服强度为252 MPa，密度为7800 kg/m³，泊松比为0.29，弹性模量为210 GPa。在齿轮系统底面添加固定约束，赋予其重力属性，设置驱动轮表面为接触面，从动轮表面为目标面。

综合计算效率与准确度，网格划分采用六面体单元，驱动齿轮产生38,907个节点，33,320个单元，从动齿轮产生87,388个节点，71,856个单元，装配体网格划分情况如图6所示。

Figure 6. Gear assembly meshing diagram

图6. 齿轮装配体网格划分图

3.2.3. 模态仿真结果与分析

对齿轮传动系统进行模态分析，导入的模型、网格划分、接触类型等与静力分析条件一致，给定电机输出额定扭矩，将边界条件更改为固定齿轮下表面，前8阶频率与振型分析如图7以及表3所示。

(一阶) (二阶) (三阶) (四阶) (五阶) (六阶) (七阶) (八阶)

Figure 7. Gear system modal vibration patterns

图7. 齿轮系统模态振型图

Table 3. Gear system intrinsic frequency and corresponding vibration pattern

表3. 齿轮传动系统固有频率及相应振型

通过查看前八阶模态分析结果，可以看出第一阶模态振型偏向整体变形，从动齿轮表面一端变形最大，第二阶与第三阶模态振型偏向对折振动，第四阶与第五阶模态振型的振幅峰值分布四处，第六阶与第七阶模态振型的振幅峰值分布六处，第八阶模态振型的振幅峰值分布八处。在额定输出扭矩载荷下，齿轮传动系统前八阶固有频率相差不大，说明该关节设计符合工作要求，齿轮啮合频率计算公式如下式：

$f=\left(Z_1+Z_2\right)\times \frac{n}{2}$ (3)

其中， $f$ 是齿轮啮合共振频率， $Z_1$ 与 $Z_2$ 表示两个齿轮齿数， $n$ 表示齿轮转速，可以得到正常运行的共振频率(0~3960Hz)，均低于表3中各阶模态固有频率，则齿轮系统不会发生共振。

3.3. 瞬态动力学分析

齿轮传动系统是一个强非线性结构，对其进行动力学分析可以判断给定载荷下工作的可靠性，齿轮传动系统除了受旋转关节和下抱臂负载的重力之外，还有动力源旋转伺服电机频繁启停、变速产生的惯性力。在齿轮受外力驱动旋转的状态下，齿轮结构会产生一定的旋转预应力，预应力的存在会使齿轮系统的结构刚度产生变化，从而影响固有频率，齿轮啮合接触面与齿根处作为齿轮系统中薄弱位置，发生齿面接触和齿根断裂齿也是引起大部分齿轮失效的诱因。

3.3.1. 瞬态动力学理论

瞬态动力学分析实质上是当载荷作用在时域内随机变化时，分析结构动力响应的技术。其输入数据是作为时间函数的载荷，而输出数据是随时间变化的应力和位移等参数。对于强非线性结构的齿轮传动系统，在Abaqus中采用隐式动力学模块进行分析，由经典力学理论可知，物体的动力学方程为：

$\left[M\right]\left\{\ddot{x}\right\}+\left[C\right]\left\{\stackrel{\dot{}}{x}\right\}+\left[K\right]\left\{x\right\}=\left\{F\left(t\right)\right\}$ (4)

式中， $\left[M\right]$ 是质量矩阵； $\left[C\right]$ 是阻尼矩阵； $\left[K\right]$ 是刚度矩阵； $\left\{\ddot{x}\right\}$ 为节点加速度矢量； $\left\{\stackrel{\dot{}}{x}\right\}$ 为节点速度矢量； $\left\{x\right\}$ 为节点位移矢量。在Abaqus中，瞬态动力学有两种求解方法，分别是隐式求解法和显示求解法。隐式求解法基于虚功原理，需进行迭代计算，而显示求解法基于动力学分析，通常不需要迭代计算。

3.3.2. 载荷与边界条件设置

齿轮传动过程中由驱动轮、从动轮共同承受扭矩载荷，且在启动工况时最大。建立齿轮啮合过程瞬态动力学分析步，时长1秒，边界条件为释放驱动齿轮与从动轮Z轴转动方向，约束其余全部自由度，输出扭矩可以转化为驱动齿轮参考点所受的扭矩载荷或角位移；设置驱动齿轮上角位移按线性方式从零增加到设定值为载荷条件，该设定值由表2旋转关节电机扭矩计算得到，当电机转速低于、等于、高于额定转速时，输出扭矩分别为159.2 N·M、127.3 N·M、106.1 N·M。

3.3.3. 瞬态动力学仿真结果与分析

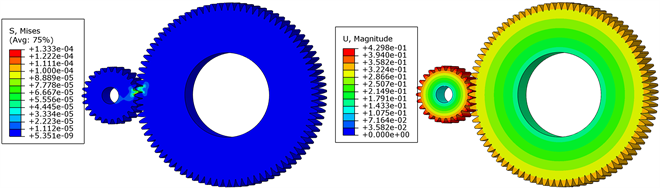
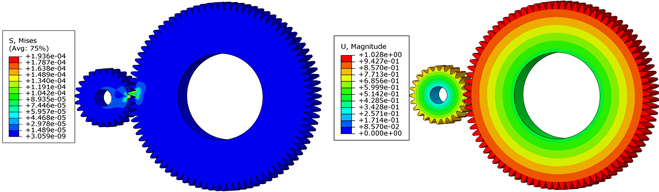
根据达朗贝尔原理 [11] ，通过惯性力的施加将动力学问题转换为静力学问题，当扭矩负载分别设置为159.2 N·M、127.3 N·M、106.1 N·M时，三种工况应力应变分析结果如图8中的(a)、(b)、(c)所示。

由图8齿轮系统应力应变分布云图可知，当电机处于输入最大转速时扭矩载荷最小，最大接触应力为723.1 Pa，最大等效位移为1.729 mm。而在实际工作中，电机从静止到设定转速有一个缓慢增加的过程。基于上文仿真，绘制齿顶圆至齿根圆单元节点应力变化曲线如图9所示。

(a) 扭矩负载159.2 N·M

(b) 扭矩负载127.3 N·M(c) 扭矩负载106.1 N·M

Figure 8. Gear transmission system stress-strain distribution cloud map

图8. 齿轮传动系统应力应变分布云图

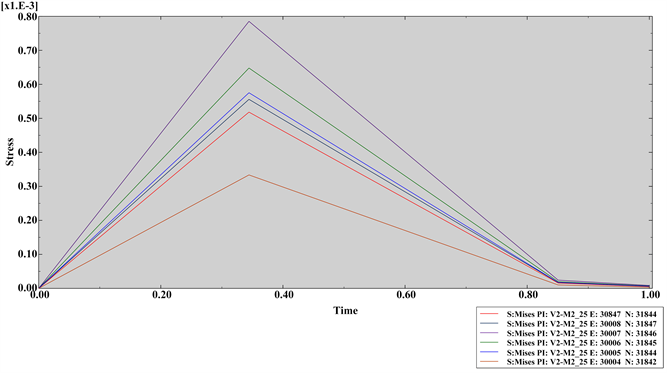
Figure 9. Gear meshing unit stress variation curve

图9. 齿轮啮合单元应力变化曲线

由图9可得，齿轮啮合运动经过0.35秒后，各单元接触应力达到最大值，通过该啮合点后接触应力开始降低。其中位于齿顶圆部位的E: 30004/N: 31842单元接触应力数值最小，仅为325 Pa，变化的速率最慢，位于齿根圆部位的E: 30007/N: 31846单元接触应力数值最大，达到723.1 Pa，变化的速率也最快。通过时域变化曲线可以得出结论：齿轮在啮合过程中接触应力持续增加，达到啮合点时该接触应力达到最大；同一时刻，靠近齿根处所承受的啮合应力更大，由此推出齿根处最易发生断齿失效的结论。

3.4. 齿轮啮合接触面应力计算

针对3.3中电机输入最大转速时，齿轮啮合系统最大接触应力为723.1 Pa，验证其他时域中任意啮合点所受应力均小于仿真值，通过赫兹应力计算公式判断金属表面接触疲劳强度极限 ${\sigma }_H$ 是否满足设计要求。赫兹方程最早由德国物理学家Heinrich Rudolf Hertz，用于研究接触物体在相互作用下的变形与应力分布规律，Hertz公式 [12] [13] [14] 常被用以计算两个接触面之间的接触应力、弹性系数等。

3.4.1. 赫兹应力理论

基于齿轮啮合系统，分析齿轮节点接触应力和最大接触应力的差异，忽略接触面材料、表面粗糙度、载荷等因素影响，创建理想数学模型。由Hertz公式可得啮合齿轮齿廓任意一点接触应力计算公式 [15] 为：

${\sigma }_H=\sqrt{\frac{Fn}{\pi L}\frac{1/{\rho }_1\pm 1/{\rho }_2}{\frac{1-{\mu }_1^2}{E_1}+\frac{1-{\mu }_2^2}{E_2}}}$ (5)

式中： $F_n$ 为法向载荷， $L$ 为接触线长度， $\rho$ 为齿廓上的曲率半径， $\mu$ 是齿轮材料泊松比， $E$ 是材料的弹性模量，变量下标1、2分别代表驱动轮、从动轮，正号用于外啮合，负号用于内啮合。研究表明齿根部分靠近节线处最易发生点蚀 [16] [17] [18] ，故常取节点处的接触应力作计算依据，公式(5)经过简化处理得到齿面接触强度计算公式：

${\sigma }_H=2.5Z_E{Z}_{\epsilon }\sqrt{\frac{2K_H{T}_1}{b{d}_1^2}\frac{u\pm 1}{u}}$ (6)

其中， $K_H$ 为载荷修正系数， $Z_E$ 为弹性系数， $Z_{\epsilon }$ 为重合度系数， $T_1$ 为扭矩， $b$ 为齿宽， $d_1$ 为驱动齿轮节圆直径， $u$ 为齿数比。

其中弹性系数 $Z_E$ 是用以考虑弹性模量 $E$ 和泊松比 $\mu$ 对赫兹应力的影响，计算公式如下：

$Z_E=\sqrt{\frac{1}{\pi \left(\frac{1-{\mu }_1^2}{E_1}+\frac{1-{\mu }_2^2}{E_2}\right)}}$ (7)

当两齿轮均为钢材时，基于公式(7)可得：

$Z_E=\sqrt{\frac{E}{2\pi \left(1-{\mu }^2\right)}}$ (8)

当齿轮弹性模量不同时，其当量弹性模量为：

$E=\frac{2E_1{E}_2}{E_1+E_2}$ (9)

重合度系数 $Z_{\epsilon }$ 是用以考虑重合度对单位齿宽载荷的影响，计算公式以及端面重合度 ${\epsilon }_{\alpha }$ 近似计算公式如下 [19] ：

$Z_{\epsilon }=\sqrt{\frac{4-{\epsilon }_{\alpha }}{3}}$ (10)

${\epsilon }_{\alpha }=\left(1.88-3.2\left(\frac{1}{z_1}\pm \frac{1}{z_2}\right)\right)\cos \beta$ (11)

3.4.2. 齿轮啮合应力计算与分析

本文研究的齿轮系统各参数如下：设定驱动轮输入扭矩 $T_1$ 为106.1 N·M， $K_H=1$ ，齿宽计算公式 $b=m\times z_c$ ，其中齿轮模数 $m=2$ ，齿轮系数 $z_c$ 通常取0.8，则 $b=1.6$ ，驱动轮齿数 $z_1$ 为25，则 $d_1=m\times z_1$ ，为50 mm，从动轮齿数 $z_2$ 为85，则传动比 $u$ 为25/85。齿轮弹性模量 $E_1=206\text{GPa}$ ， $E_2=210\text{GPa}$ ，齿轮泊松比 ${\mu }_1$ 与 ${\mu }_1$ 均为0.29，螺旋角系数 $Z_{\beta }$ 为1，则 $\cos \beta$ 为1。结合机械手册，将上述参数分别代入公式(8)、(9)、(10)、(11)计算，得到当量弹性模量 $E\approx 207.98\text{GPa}$ ，弹性系数 $Z_E\approx 6$ ，重合度系数 $Z_{\epsilon }\approx 0.8729$ 。将上述数据代入公式(6)，求得啮合齿轮系统节点处接触疲劳强度极限近似为：

${\sigma }_H=2.5\times 6\times 0.8729\sqrt{\frac{2\times 1\times 106.1}{1.6\times 50\times 50}\times \frac{25/85+1}{25/85}}\approx 6.3258\text{MPa}$

计算得到该齿轮传动系统接触疲劳强度极限为6.3258 Mpa，低于材料许用应力355 MPa，远高于上文中齿轮根部最大接触应力723.1 Pa。经过理论与仿真分析，验证齿轮传动系统符合工作强度指标。

4. 结论

根据机器人工作范围与各关节协作完成任务的需求，研制一款协作机器人，设计机器人的外观结构与运动方案，利用Solidworks完成整机的建模。基于机械臂单元展开研究，针对预防齿轮系统失效的问题对旋转关节齿轮传动结构进行Abaqus仿真分析，验证了该结构的低阶振型以从动齿轮振动为主，固有频率符合应用要求；得到啮合齿轮装配体在驱动源输出不同扭矩负载情况的应力应变分布云图，结合有限元仿真与赫兹理论，得出齿根处接触应力在齿轮啮合至分度圆时最大的结论，齿轮接触疲劳极限低于材料屈服强度，且远高于仿真中得到的齿根最大接触应力。

综上，本研究目前已完成了送餐机器人整机的结构设计和样机加工调试，对机械臂关键部位进行仿真实验，将理论结果与实际测试进行分析对比，为机械臂各关节模组的进一步优化提供了理论依据。

NOTES

^*通讯作者。