1. 引言
渗流是流体在多孔介质中的流动，流体渗流的特征涉及到流体的性质、多孔介质的性质和流动的状况以及它们之间的相互作用[1] 。低渗透岩心驱替实验和开发的实践表明：低渗透储层中，油气渗流不符合达西定律，即存在启动压力梯度和非线性渗流[2] -[9] 。现有的描述低渗透多孔介质中渗流的主要模型有：拟压力梯度模型[10] 、分段模型[10] 、多参数模型[11] -[13] 等。
在分析低渗透油藏的渗流模型时，我们发现指数模型与实验符合的很好，于此同时，指数模型中得到的1次、2次、3次、4次模型有不同的特点，本文通过典型的实例对渗流模型的函数进行分析。
2. 静态边界层为整个流动区域的渗流模型分析
假设：在驱动力趋近于0时，整个流体都是粘滞层，所以在微管中，粘滞层的厚度就是微管的半径，结合边界黏附层的变化特征，可以假设
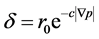(1)
式中：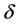
为边界黏附层厚度，
；
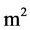为微圆管半径，
；
为边界黏附层参数，
。
如图1为半径为5微米的石英圆管中，去离子水的流动实验得到的边界黏附层厚度[14] ，经拟合表现出了很好的指数特征。
2.1. 牛顿流体在微圆管中的速度及流量公式
根据牛顿流体的应力应变关系，
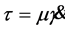(2)
Figure 1. The relationship between boundary layer thickness and shear rate changes, a radius of 5 mm quartz tube
图1. 微圆管半径为5 mm的边界层厚度随剪切率的变化关系
式中，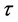
为流体所受的应力，
；
为流体的应变，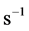
。
对于圆形的管道，方程(6)可以具体表达为，
(3)
式中，
为圆管径向坐标，
。
假设边界黏附层的厚度为
，相当于有效流动半径减小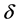
，对方程(7)从
到
进行积分，得到了考虑负滑移时，流体在圆管中的速度分布，
(4)
将公式(1)代入公式(4)中得，
(5)
再对公式(5)进行过流断面上的积分，就可以得到对应的流量公式，
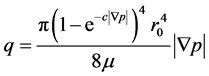(6)
对于方程(6)，当压力梯度较大时，可以回归于Poisuelle流量公式：
(7)
在计算中，我们发现指数是产生非线性的主要因素，方程(6)中的4次方的影响只是程度大小，因此引进n次方模型，进行详细分析：
(8)
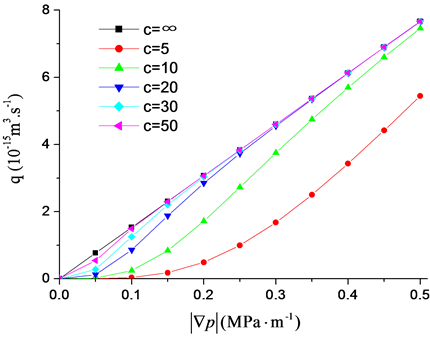
假设水在半径为2.5微米的微圆管中流动，粘度为
(20℃下)，由公式(8)可以计算出微管中的流量，如图2所示：1) 当压力梯度较小时，非线性特征明显。2)
值越小，非线性的情况越严重[15] 。
从图2可以看出：无论括弧上方是几次方(1~4)的函数，均可以表达出非线性的特征，其区别在于：在相同的c下，偏离线性的程度随着次方数的增大而增大。因此对于表象的实验拟合，可以用更简单的方式进行描述，即一次方的形式：
(9)
当压力梯度较小时，(9)式可以近似为抛物线方程：
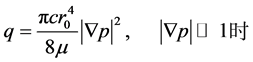(10)
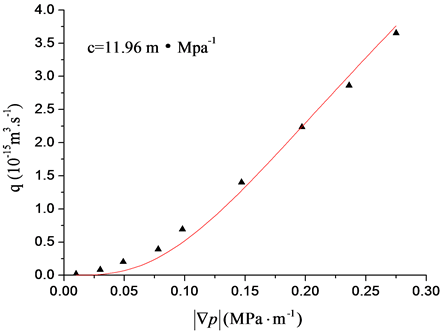
用去离子水在半径为
中微圆管中，进行流动实验研究[15] ，所得的结果如图3所示：很明显一次和二次方和一次方的模型更好地拟合了实验结果。
2.2. 启动压力梯度的悖论
在低渗透油藏中，常称具有启动压力梯度，从公式(8)的分析中，当压力梯度较大时，流量公式变为
(4次方) (3次方) (2次方) (1次方)
Figure 2. A radius of 2.5 mm micro circular tube, different values of c of pressure gradient and flow diagram
图2. 微圆管半径为2.5 mm不同c值的压力梯度与流量的关系图
(4次方) (3次方) (2次方) (1次方)
Figure 3. A radius of 2.5 mm micro circular tube, pressure gradient and flow diagram
图3. 微圆管半径为2.5 mm的压力梯度与流量的关系图
方程(11)
(11)
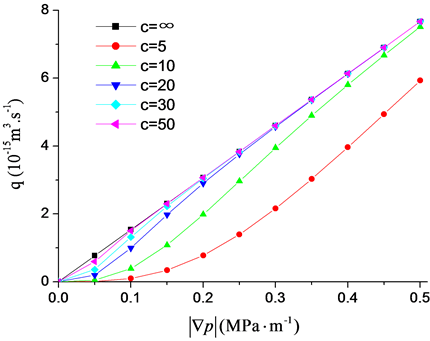
从方程(11)并不能看出什么压力梯度，即从压力梯度较大的线性段，向前延长较于坐标原点，即截距是零，并没有什么启动压力梯度，但为什么工程实践和实验中观测到启动压力梯度？那时因为：在实验中压力梯度还是没有足够的大，还处在某个非线性较弱的流动阶段，因此实践中总是利用最后的两、三个数据点进行线性化延长，而得到截距，即所谓的启动压力梯度。如图2可以明显的看出这一下，图4为不同压力梯度下的情形，也可以说明这点。
从图4清晰地看到了“启动压力梯度”的悖论：从某种程度上，启动压力梯度是存在的，但从全局看：启动压力梯度是不存在的，它只是局部条件下的产物，就像盲人摸象一般：局部代替不了整体，整体特征也代替不了局部。
3. 牛顿流体在低渗透多孔介质中的渗流模型
对于多孔介质，可以利用毛管束模型分析相应的渗流公式，可得低渗透多孔介质中的渗流公式为
(小压力梯度范围) (大压力梯度范围)
Figure 4. A radius of 2.5 mm micro circular tube, different values of c of pressure gradient and flow diagram
图4. 微圆管半径为2.5 mm不同c值的压力梯度与流量的关系图(4次方公式)
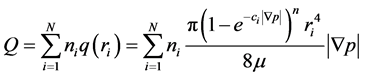(12)
定义渗流速度为
(13)
可得，渗流公式为
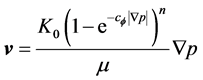(14)
其中，
，
，
为平均边界黏附层参数。
为了分析公式(14)的物理含义。假设原油在某一维低渗透多孔介质中的流动特征，其过流面积为10 m2，渗透率为0.001 mm2，原油粘度为10 mPa·s，由公式(14)可以计算油流量随压力梯度的变化。如图5所示：当
值较大时(c = 0.5)，流动特征接近于达西渗流的线性流动，当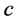
值较小时(c = 0.01)，就可以明显地看到小压力梯度下的流量减小，偏离达西流。当
趋于无穷大时，公式(14)为达西定律。这说明模型(14)能够很好地描述了低渗透多孔介质中的渗流特征。
图6是用公式(14)对实验数据的拟合，实验流量数据见表1。从图6中可以清楚看到公式(14)可以描述出实验数据的非线性规律。根据图3和图5我们可以看到：方程(11)和(14)无论是对于微圆管，还是对于低渗透多孔介质，它们都可以很好地描述驱动压力梯度所有范围内的流量，尤其以二次方和一次方的模型最好，因此这两个公式可以应用于实际的工程实例计算。
(4次方) (3次方) (2次方) (1次方)
Figure 5. Pressure gradient and flow diagram in low permeability porous media
图5. 低渗透多孔介质中压力梯度与流量的关系图
Table 1 . The experimental data of Figure 6
表1. 图6的实验基本数据
4. 结论
本文经过对现有低渗透油层非达西渗流的模型的分析，从微圆管流动中的边界黏附层的特征出发，推导了具有边界黏附层的流体在微圆管中的速度及流量公式，最后得到了低渗透多孔介质中，考虑边界流体黏附层的渗流模型，并且进行了举例分析。研究结果表明：低渗透油层在整体上不存在启动压力，但在压力梯度较小的局部，可以认为存在拟启动压力梯度；通过对实验数据的不同次方拟合，我们可以比较出指数函数1次方拟合的相对准确。
基金项目
国家重点基础研究发展计划(2013CB228002)。
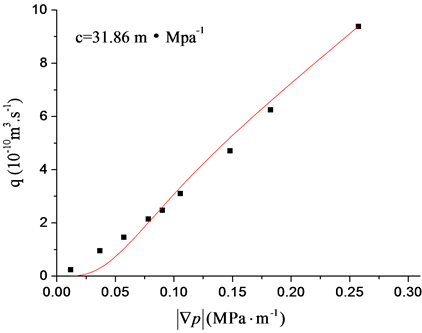
(4次方) (3次方) (2次方) (1次方)
Figure 6. The experimental data fitting of pressure gradient and flow rate in low permeability porous media
图6. 低渗透多孔介质中压力梯度与流量的实验数据拟合
NOTES
*通讯作者。