1. 引言
OLAP系统中,频繁需要在大规模数据仓库上进行复杂的查询,为了提高查询速度,往往需要事先物化一些视图。视图物化是提高数据仓库性能的最有效技术之一。物化了的视图是一种通过预计算中间结果来提高数据访问的物理结构。进行视图物化首先要解决视图大小的估算问题。
近年来对于视图大小的估算研究很多。典型的OLAP查询由选择和聚合数据(通过GROUP BY语句实现)构成[1] 。通过预计算,许多似是而非的组集可以避免由于大数据表上的聚合引起的响应速度减慢。许多查询,如那些包含条件(HAVING clause)可以利用预先聚合加快计算速度。然而物化视图需要额外的存储空间。而导致在数据仓库刷新时产生维护开销。此外,视图的数据量很大:在一个d维的数据立方体中,视图的数量是2d[1] 。因此,在数据仓库的物理设计中物化视图的选择是非常重要的,是一个NP困难问题[2] 。一些视图大小估算技术假设数据的分布是“谦虚”的,通常假设是均匀的分布[3] ,但是任何数据分布的偏差均将导致过高的估计结果。
一般的,当统计假设估计量较快完成计算那么代价最大的步骤可能是随机抽样。其误差可能比较大,且不能成为被束缚的先验。这里将讨论基于概率的估算(Probabilistic Counting) [4] 、重对数概率估算(LOGLOG Probabilistic Counting) [5] 、修正算法(Adaptive Counting) [6] 。代价相对大、相对平易的估计量倾向于提供较高的精确度和可靠性[7] 。
为了使用这些技术,需要将列进行快速散列(Hashing),理论边界需要至少两两独立的散列值。幸运的是,当在数据立方体中具有较多维数(d > 10)每一维值相对可用内存来说通常是小的。因此可以对每一维分别进行散列。将结果存储于主存之中,将这些完全独立的一维的散列值合并为独立的d型多维散列值。
当分配较多单元时,算法更为精确,但速度减慢。文章中设计了两种使用场合,一种情况是期望粗略估计,误差可达10%,尽可能的快速估算,这时可使用较小的存储预算(少于1 MB);另一种情况是期望精确计算,误差小于1%,甚至0.1%,这时使用数MB的内存。
2. 多重分型模型的估算
这里在多重分型模型之上实现了各种算法[8] 。给定一个样例,对于多重分型模型所有需要研究的是每个样例F0中相异的元素数量,样例N’中的元素数量,所有元素的总数N,以及样例mmax中最频繁出现项的数量。因此,一种简单的实现是可能的(见Algorithm 1)。算法内存的使用由取样上的GROUP BY查询决定(line 6):通常,一个较大的样例将导致更为重要的内存使用。
3. 随机散列
散列以随机的方式进行。从元组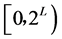 的散列函数中。
的散列函数中。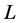 是定值(
是定值(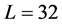 或
或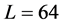 )在
)在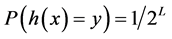

Algorithm 1. View-size estimation using a multifractal distribution
的前提下,对所有的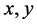 ,散列是统一的,也就是说所有的散列值是近似平等的。对所有的
,散列是统一的,也就是说所有的散列值是近似平等的。对所有的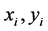 ,如果
,如果
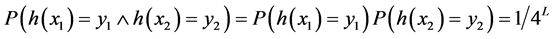
那么散列是两两独立的,而两两独立暗示着均匀性。对所有的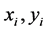 ,如果
,如果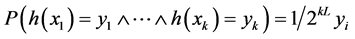 ,则为独立的k型智能单元。最后,若对所有的k值均为k型智能单元,那么散列是完全独立的散列值,需要
,则为独立的k型智能单元。最后,若对所有的k值均为k型智能单元,那么散列是完全独立的散列值,需要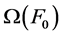 个单元的内存[9] 。
个单元的内存[9] 。 很大时将是不切实际的。
很大时将是不切实际的。
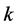 型独立单元的散列值可在多维数据仓库中高效计算。对每一维
型独立单元的散列值可在多维数据仓库中高效计算。对每一维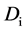 ,建立一个查找表
,建立一个查找表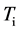 ,以
,以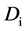 值作为主键。每当遇到一个新的主键值,生成一个
值作为主键。每当遇到一个新的主键值,生成一个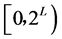 之间的随机数,并且将其存放在查找表
之间的随机数,并且将其存放在查找表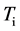 中,这个随机数即此键值的散列值。在数据仓库的索引中,维数众多,每一维通常具有几个不同的值,因此,查找表经常至少需要使用几兆的内存。当散列
中,这个随机数即此键值的散列值。在数据仓库的索引中,维数众多,每一维通常具有几个不同的值,因此,查找表经常至少需要使用几兆的内存。当散列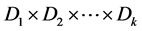 上的一个元组
上的一个元组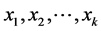 ,其散列值为
,其散列值为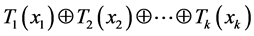 这里
这里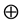 为异或。此散列为
为异或。此散列为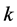 型智能单元,需要固定的时间完成。表
型智能单元,需要固定的时间完成。表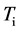 可被几个估算多次使用:可同时估算在
可被几个估算多次使用:可同时估算在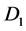 和
和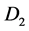 上的GROUP BY和
上的GROUP BY和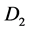 和
和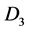 上的GROUP BY的视图大小。但只需一个单独的表
上的GROUP BY的视图大小。但只需一个单独的表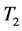 。
。
4. 算法描述
论文中选用Probabilistic Counting (基于概率的估算) [4] 的算法描述如Algorithm 2所示。选用的LOGLOG Probabilistic Counting (多重对数概率估算)是一个加速的变体[5] 。这两种算法的主要区别在于LOGLOG算法只跟踪前导零的最大值,而概率算法跟踪前导零的所有观测值。而且对于散列值中的离群值更具弹性。通过实践得到的对于同一参数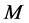 对这两种算法使用的比较结果如下:概率算法使用
对这两种算法使用的比较结果如下:概率算法使用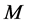 个计数器存放从1至
个计数器存放从1至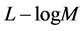 的整数。假设独立散列,这两种算法产生相对标准误差分别为
的整数。假设独立散列,这两种算法产生相对标准误差分别为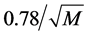 和
和

Algorithm 2. View-size estimation using Probabilistic Counting
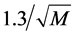 。这些理论上的结果假设为独立散列的,实际上是不能实现的,而且要求视图的大小非常大,但是却可以检测小视图。一个小视图相对可用内存M来说,可剩下M个计数器中的几个不用(Algorithm 2中的序列
。这些理论上的结果假设为独立散列的,实际上是不能实现的,而且要求视图的大小非常大,但是却可以检测小视图。一个小视图相对可用内存M来说,可剩下M个计数器中的几个不用(Algorithm 2中的序列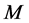 )。当超过5%的计数器剩余未用,返回线性计数估算而不是重对数估算[10] (见Algorithm 3最后一行)。
)。当超过5%的计数器剩余未用,返回线性计数估算而不是重对数估算[10] (见Algorithm 3最后一行)。
5. 实验结果
为了进行上述算法的精确度和速度的对比实验,利用测试数据生成程序DBGEN生成了规模因素参数等于2的测试数据集,大小为1.5 G。从测试数据集中选择了8个视图,这些视图有2个视图是4维以上的结构。这里标准误差使用对真实值的偏差或由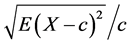 确定。这里的
确定。这里的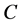 是需要估计的值。标准误差(相对)定义为误差的偏离值,通过上式利用20次的估算计算所得。
是需要估计的值。标准误差(相对)定义为误差的偏离值,通过上式利用20次的估算计算所得。
实验运行环境为英特尔双核至强处理器(2.66 GHz),内存2G,GUN C++ 编译器4.0.2。选用GUN/CGI STL扩展hash-map作为C++标准集成unordered_map,提供插入和查询的摊销 。其它的查找表使用STL map模版建立,具有红黑树的计算复杂度。所采用的测试内容包括每种估算技术GROUP BY查询随机种子和内存的大小、与这些参数相关的每一步计算GROUP BY视图的大小及其生成时间。同样的,对多重分型估算技术计算每个GROUP BY的时间与估算大小采样率和随机种子。
。其它的查找表使用STL map模版建立,具有红黑树的计算复杂度。所采用的测试内容包括每种估算技术GROUP BY查询随机种子和内存的大小、与这些参数相关的每一步计算GROUP BY视图的大小及其生成时间。同样的,对多重分型估算技术计算每个GROUP BY的时间与估算大小采样率和随机种子。
5.1. 精确度分析
从DBEGEN产生的数据集上运行各种算法得到了每种算法的标准误差(见图1)。
由于DBGEN使用一个统一的分布,基于模型的多重分型技术是特别精确的。正因如此,DBEGN是一个较弱的工具来检测基于模型的视图估算算法。但由于忽略数据分布,文中的这三种算法不存在这种问题。
5.2. 速度分析
在测试数据集上通过上述算法估算所有视图大小所需总时间为7 min。对多重分型技术,所有的估算
Figure 1. Standard error comparison of view-size estimation algorithms
图1. 随M增大每种估算算法的标准误差分析
(a) 多重分型(Multifractal) (b) 基于概率的估算(Probabilistic Counting) (c) 多重对数概率估算(LOGLOG Probabilistic Counting) (d) 修正算法(Adaptive Counting)

Table 1. Running times of the algorithms
表1. 算法运行时间
m1=256; m2=8388608; (1): LOGLOG; (2): Probabilistic; (3): Adaptive Counting
约在2秒内完成。进一步实验,在一个5 GB大小的数据集上,突出每一个处理步骤的用时:装载和解析数据、散列和估算视图的大小(见表1)。所有算法的运行时间对维数是相当敏感的。对低维(高维)视图,相关更多的时间花费在读取数据上(散列数据)。然而,散列时间和读取时间远大于其余花费在计算的时间。实验结果表明修正算法(Adaptive Counting)不管视图大小如何均提供紧密的估算而且当增大存储预算时,可保持较快的估算速度。
6. 结束语
文章分析了3种用于数据仓库环境的视图大小估算算法,通过实验数据得出了各种算法的标准误差,修正算法(Adaptive Counting)提供较为稳定的估算,不受视图大小的影响。存储预算较小时,几种算法的速度相差不大,而增大存储预算时,修正算法仍可保持较快速度。

NOTES
*通讯作者。