1. 引言
学生成绩综合评价是教育评价的重要内容，当前关于学生成绩的综合评价论文很多，提出了多种学生成绩综合评价方法，有算术平均法、平均学分绩法、主成分分析法、TOPSIS法等等[1] -[3] ，这些方法从不同侧重点建立了成绩评价模型。
针对军队院校，学员的培养关系到我军的未来军官队伍的建设，关系到我国未来的国防建设，在军校的人才培养方案中，更注重的是学员的综合素质，学员综合素质评价至关重要。
层次分析法(AHP)是对一些较复杂、较模糊的问题做出决策的简易方法，已经在经济管理、能源交通、教育和军事等领域得到了非常广泛的应用[4] 。张卫东[5] 利用AHP方法确定新兵综合素质考评中各科目的相对权重，建立了层次结构模型，对新兵的综合素质进行了定量分析和计算。
据此本文根据层次分析法的原理，考虑学员的综合素质，从学员的科学文化素质、军事素质、思想政治素质、领导管理素以及创新能力等方面对学员进行综合素质评价。
2. 层次分析法及评价体系的建立
2.1. 建立递阶层次结构
应用AHP解决实际问题，首先明确要分析决策的问题，并把它条理化、层次化，理出递阶层次结构。
AHP要求的递阶层次结构一般由以下三个层次组成：目标层(最高层)、准则层(中间层)、方案层(最低层)。
通过对军校学员综合素质评价问题的综合分析，确定目标层(A)为军校学员的综合评价；共设两个准则层分别为B准则层和C准则层，B准则层共分为五个因素，分别为科学文化素质(B1)，军事素质(B2)，思想政治素质(B3)，领导管理素质(B4)，创新能力(B5)；C准则层共有10个因素，分别为平时成绩(C1)，考核成绩(C2)，体能素质(C3)，理论水平(C4)，思想素质(C5)，日常表现(C6)，领导管理能力(C7)，心理素质(C8)，竞赛(C9)，科技发明(C10)；方案层(D)共分为两个方面，评级(D1)，排名(D2)。各层次的具体关系如图1所示。
2.2. 构造判断矩阵并赋值
1) 为确定决策实行的方案和各名学员的决策情况，则需要对决策的各方面权重进行确定，由于尚未给出确定的权重，因此采用AHP法分析确定决策各方面权重，从而确定模型的求解。
2) 为了使判断矩阵更具科学性，向专家反复询问：针对判断矩阵的准则，其中两个元素两两比较哪个更重要，重要多少，对重要性程度按1~9赋值(重要性标度值如表1)，构造各级判断矩阵。
设填写后的判断矩阵为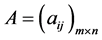
，判断矩阵具有如下性质：
①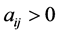
②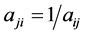
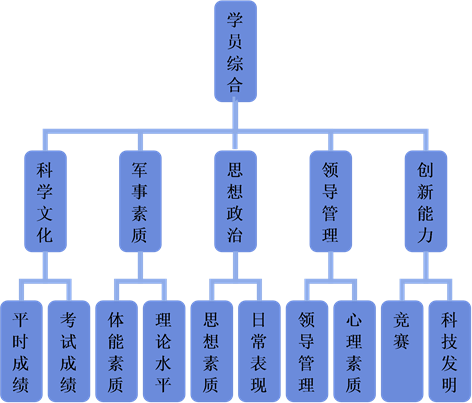
Figure 1. Hierarchical Structure
图1. 递阶层次结构
Table 1. The importance of scale value
表1. 重要性标度值表
③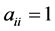
当上式对判断矩阵所有元素都成立时，则称该判断矩阵为一致性矩阵。
2.3. 层次单排序(计算权向量)
对于构造的判断矩阵，进行层次排序。
对于一致性判断矩阵，每一列归一化就是相应的权重。对于非一致性判断矩阵，每一列归一化后近似其相应的权重，再对这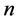
个列向量求取算术平均值作为最后的权重。具体公式是：
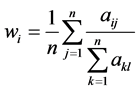
需要注意的是，在层次排序中，需要对判断矩阵进行一致性检验。
2.4. 层次单排序的一致性检验
计算一致性指标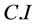
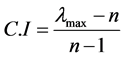
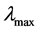为判断矩阵的最大特征根。
查表2确定相应的平均随机一致性指标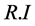
[6]
计算一致性比例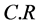
，并进行判断
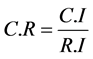
当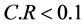
时，认为判断矩阵的一致性是可以接受的；当
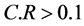时，认为判断矩阵不符合一致性要求，需要对该矩阵进行重新修正。
2.5. 层次总排序与一致性检验
总排序是指每一个判断矩阵各因素针对目标层(最上层)的相对权重。这一权重的计算采用从上而下的方法，逐层合成。
很明显，第二层的单排序结果就是总排序结果。假定已经算出第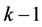
层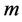
个元素相对于总目标的权重
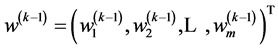，第
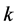层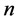
个元素对于上一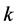层(第
层)第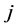
个元素的单排序权重是
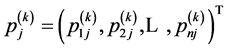，其中不受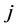
支配的元素权重为零。令
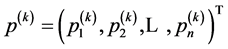，表示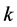第
层元素对第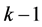
层个元素的排序，则第
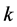层的元素对于总目标的总排序为：
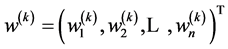
或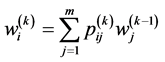
，
。
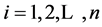同样，也需要对总排序结果进行一致性检验。
假定已经算出针对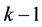第
层第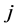
个元素为准则的
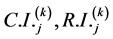和
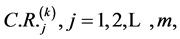则第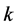
层的综合检验指标
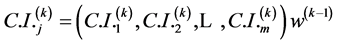
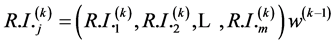
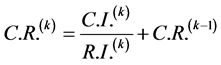
当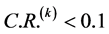
时，认为判断矩阵的整体性是可以接受的。
以下为层次总排序及检验结果：(表3，表4)
可以看出，总排序的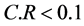
，认为判断矩阵的整体一致性是可以接受的。
Table 2. The mean random consistency index
表2. 平均随机一致性指标
Table 3. The total order of C level (C.R = 0.000)
表3. C层次总排序(C.R = 0.000)
Table 4. The total order of D level (C.R = 0.000)
表4. D层次总排序(C.R = 0.000)
Table 5. The comprehensive quality evaluation results of the 10 students
表5. 10名学员的综合素质评价结果
从方案层总排序结果看，排名的权重大于评级的权重，因此，最终的决策方案是排名。综合素质评价各指标权重为各层次指标层次总排序权重。
3. 学员综合素质评价
在获得各个指标的权重后，为了科学的、有效地描述学员的综合素质，采用加权算术平均综合评价法进行综合评价，即计算综合评价指数，公式如下：
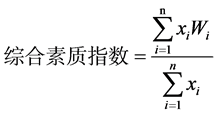
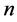是评价指标体系中的指标个数；
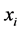是已经同度量处理过的第
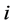个评价指标的相对值，
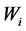为各项指标的权重，
。
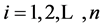通过计算可以定量的描述学员综合素质的情况，科学、客观、公正的评价了学员的能力素质。通过调查，解放军理工大学理学院7队的10名学员5种素质得分，应用以上评价方法进行综合素质评价，评价结果如表5。
4. 结果分析
利用层次分析法对各个指标的权重进行了科学的、客观的描述，对于原本复杂的学员的综合素质评价问题，能够进行比较直观和全面处理。运用这种综合评价方法能够综合评价学员的各项素质，能够客观公正的反映学员的各项能力水平，对于一名军校大学生来说，学习和体能是重中之重，其他各项素质也是学员以后走上工作岗位所必备的，因而在评价时不能漏掉其他方面。
基金项目
本文获得解放军理工大学理学院青年科研基金支持。