N掺杂ZnO (100)表面对其电学性质的影响
Influence of N Doping on Electronic Properties of ZnO Surface
DOI: 10.12677/CMP.2014.34007, PDF, HTML, 下载: 2,931  浏览: 8,955  国家自然科学基金支持
作者: 胡宏铎：湖北工程职业学院信息工程系，黄石；陈兰丽：江西科技师范大学江西省通信与光电子重点实验室，南昌
关键词: ZnO表面；p型；第一性原理；ZnO Surface； p-Type； First Principles
摘要: 基于密度泛函理论的第一性原理计算了N掺杂ZnO (100)表面的形成能和电学性质。首先，我们分析了N掺杂ZnO (100)表面不同层时的结构弛豫情况，接着计算了N掺杂表面的形成能和电子结构。结果表明N掺杂后体系发生较大的晶格畸变。N掺杂块体ZnO的形成能比掺杂表面时的形成低。结果表明N很容易聚集在体内而不是表面。从N掺杂ZnO (100)表面的电子结构中得知，体系的费米能级向价带移动，这主要归因于N-p态，同时体系表现为p型特征。
Abstract: A theory of formation energy and electronic properties of N doping ZnO (100) surface is proposed on the first principles based on density function theory. First, we have analyzed the relaxation of the structure of N doping ZnO (100) surface at different layers. Later, we have calculated the formation energy and electronic structure of N doping ZnO (100) surface. The results show that there is a large lattice distortion after N doping. And the formation energy is lowest in the bulk ZnO when N is doped in the bulk ZnO. The results show that N atom easily accumulates in the body instead on the surface layers. The calculated electronic structure shows that the Fermi level shifts into the valence band which is contributed by N-p states, and the system after doping demonstrates as p-type.
文章引用：胡宏铎, 陈兰丽. N掺杂ZnO (100)表面对其电学性质的影响[J]. 凝聚态物理学进展, 2014, 3(4): 46-52. http://dx.doi.org/10.12677/CMP.2014.34007

1. 引言

氧化锌是一种在紫外和蓝光发射方面具有很大前景的新型光电子材料，在半导体发光二极管、激光二极管、太阳能电池、紫外半导体激光器领域具有广阔的应用前景[1] [2] 。然而ZnO在室温下是以纤锌矿最为稳定，并且在c轴方向产生Zn和O极性，这种极性对ZnO的性质有很大影响[3] 。

最近，关于N掺杂ZnO薄膜材料很受关注。很多研究小组通过掺杂N原子来提高p-型ZnO的性质[4] 。Zhu [5] 等人通过光致放光和罗曼散射方法研究N掺杂ZnO薄膜，研究结果表明由于N的掺入，ZnO薄膜材料的特性发生很大变化。B. M. Rajbongshi [6] 研究小组报道到通过溶胶-凝胶方法合成和制备ZnO，研究结果发现掺杂N后，在吸收光谱中表现为红移。Zeng [7] 等人采用等离子体辅助的金属有机化学气相沉积的方法制备了N掺杂ZnO薄膜，体系表现为p-型特征。并且可以得到的电阻率为1.72 Ω cm的电阻率和迁移率为1.59 cm2/V s，空穴浓度为2.29 × 1018 cm−3。同时N作为受主在ZnO中的受主能级为180 meV。E. S. Tuzemen [8] 等人采用脉冲磁过滤阴极电弧沉积(PFCVAD)系统在玻璃衬底上制备N-掺杂ZnO薄膜，并且使用吸收光谱方法发现了薄膜光带隙。但由于N掺杂ZnO薄膜材料获得p-型特征的可重复性和持续性不稳定，导致研究其ZnO表面p型机制的甚少。

本文采用第一性原理基于密度泛函理论从理论上对N掺杂ZnO (100)表面的几何结构、形成能和电子结构进行研究分析。研究是否得到p型特征的ZnO (100)表面，以及掺杂后，结构弛豫情况晶格畸变情况，比较了N掺杂块体ZnO和N掺杂ZnO (100)表面两种情况。

2. 计算模型与计算方法

本文的计算工作都是基于密度泛函理论的第一性原理计算程序即在Vienna Abinit Simulation Package (VASP) [9] [10] 代码采用密度泛函理论。采用的交换关联势为广义梯度近似(GGA)。ZnO (100)表面用一块由6层ZnO组成的薄片(slab)来模拟。薄片由包含24个ZnO分子(每层4个)的原胞沿平行于表面的方向无限周期性展开而得，薄片上方有10 Å的真空层，以消除平板两端表面之间的相互作用。

在本文中，计算采用的超原胞如图1所示。其中，n1、n2、n3分别表示N原子所在的位置。(n1/n2/n3)表示第一层掺杂n1个N原子，第二层掺杂n2个N原子，第三层掺杂n3个N原子。例如：(1/0/0)表示只在第一层上掺杂1个N原子。在本文中，只考虑每一层掺杂一个N原子。通过第一性原理在总能最小的情况选择最优化结构。为了得到可靠的结果，在结构优化基础上进行静态计算。所有的计算最下面2

Figure 1. (Color Online) The calculated model of ZnO (100) surface

图1. ZnO (100)面的计算模型

层ZnO分子固定，再进行弛豫，当原子的受力小于0.01 eV/nm，计算停止。平面波的能量截断为400 eV。我们选取广义梯度近似(GGA)形式的非局域关联势。对表面布里渊区的用Monkhorst-Pack方法取4 × 4 × 1K点进行积分，其他参数与前面所计算的体材料的参数相同。测试计算表明，所取的k点数和平面波截断可以使体系总能量得到很好的收敛。

3. 结果与讨论

3.1. 几何结构

首先对ZnO (100)表面进行弛豫优化，固定下面两层ZnO，让其他四层原子进行弛豫。图2为N掺杂ZnO (100)表面的弛豫前后的示意图。如图2(a)所示，表面第一层O原子向真空层处移动0.098Å，而Zn原子向体内移动0.092Å，表面处的O-Zn键长由弛豫前的1.992Å变为1.867Å。表面处的Zn-O-Zn键角由弛豫前的108.044˚变为弛豫后的102.422˚，表面处的O-Zn-O键角由弛豫前的108.044˚变为弛豫后的117.903˚，在ZnO (100)表面处发生严重的扭曲。这个我们在前面的工作中也提到，这里是为与掺杂后的比较[11] 。弛豫发生明显的变化主要归因于量子杂化效应和库仑作用。在形成ZnO (100)表面时，在表面处的Zn和O都构成悬挂键。由于能量遵循能量最低的原则，所以表面的悬挂键进行重新组合。从而，表面氧原子轨道杂化类型为p3，导致氧原子向体外移动；而Zn原子杂化类型为sp2，导致Zn原子向体内移动。此外，由于表面的Zn原子和O原子的电负性的差别很大，从而使得在表面发生电子的转移，Zn原子的悬挂键电子向O原子转移，导致两原子之间的库能作用增强，使得表面发生收缩。

图2(b)为(1/0/0)表面的弛豫图。从图中得知，弛豫后，表面第一层的O原子坐标由(0.750, 0.441, 0.396)移动到(0.750, 0.442, 0.403)，向体外移动0.01Å。主要由于N的掺入，使得附近的O原子形成悬挂键，从而与Zn原子的库能作用加强。第一层的Zn-O键长变短为1.860 Å。表面第一层Zn原子向体内移动0.007Å。第一层的Zn原子与第二层的O原子形成的O-Zn-O键角为116.893˚，比弛豫前增大0.01˚。

图2(c)为(0/1/0)表面的弛豫图。由于N掺入到第二层中，表面的Zn-O-Zn健角由原来的116.893°增大为119.580˚。增大了2.741˚，第一层的Zn-O键长为1.882 Å，比掺杂到第一层增大了0.022 Å。

图2(d)为(0/0/1)表面的弛豫图。N掺杂到第三层的情况。第三层N的掺入使得第一层的O原子向体内

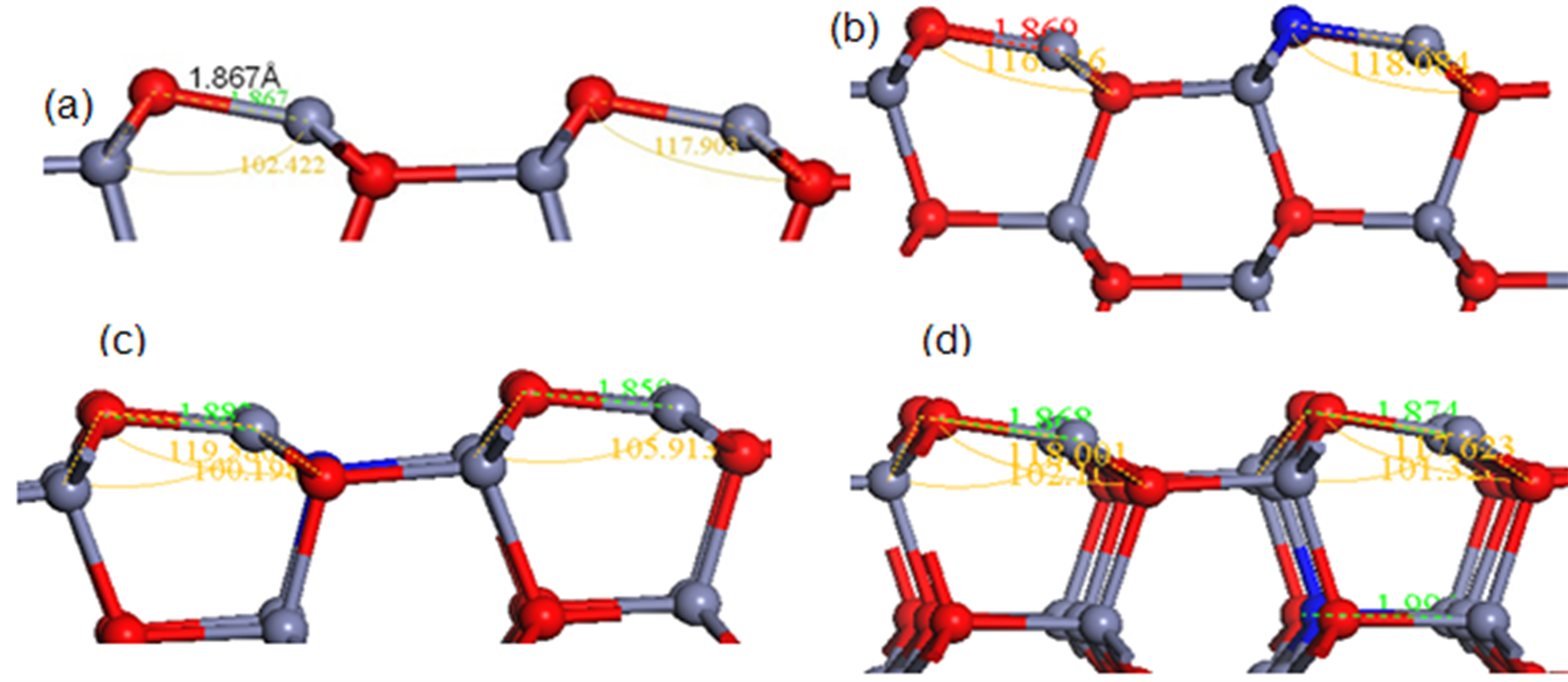
Figure 2. (Color Online) The surface structure of ZnO (100)

图2. ZnO (100)表面处的结构

移动0.001Å，第一层的Zn-O键长为1.868 Å，第一层的Zn原子与第二层的O原子形成的O-Zn-O键角为119.092˚，Zn-O-Zn形成的键角变为101.326˚，而第二层的Zn-O原子的键长变为1.996Å。

从以上的数据可以看出，当N掺杂到第一层时，第一层的Zn-O键长变长，第一层与第二层所形成的O-Zn-O键角变大，而Zn-O-Zn键角变小，第一层的O原子向体内移动的幅度较大。当N掺杂到第二层时，对第一层的影响是Zn-O键长变长，向体外移动的幅度较大，O-Zn-O键角变变大。当N掺杂在第三层时，对第一层原子的影响是Zn-O键长稍微变短，向内移动的幅度较小，键角变大。从这里得出，N掺杂在第一层第二层时，对表面的晶格畸变影响较大。

3.2. 形成能

为了研究N原子在ZnO表面内的分布情况，我们分别计算了N掺杂ZnO (100)表面上的不同位置的形成能。各种模型的形成能可以定义[12] 为：

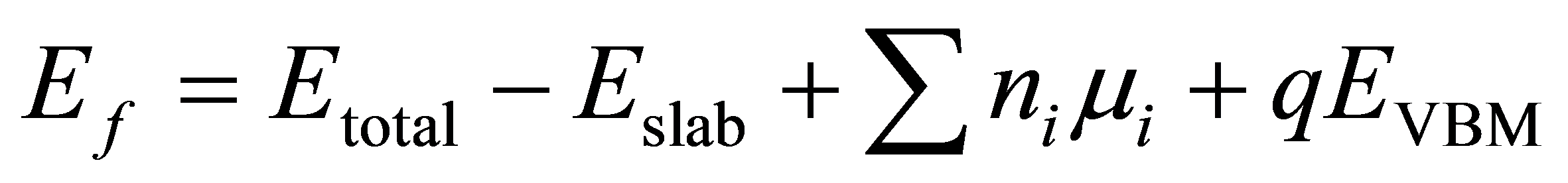(2)

其中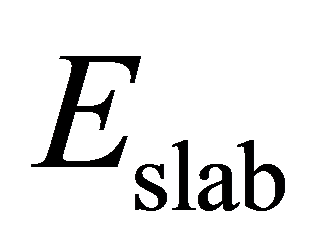为含缺陷的模型的总能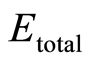；为纯净ZnO (100)表面的总能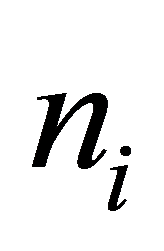；是i元素的个数，当i加进体系时，为负；当替换时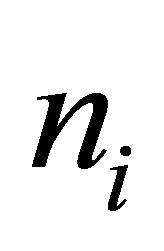，为正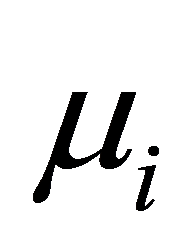；是i的化学势；为纯净ZnO相对于价带顶的能量；为了保持稳定的ZnO表面，避免其他复合体的生成，应该满足以下关系式：

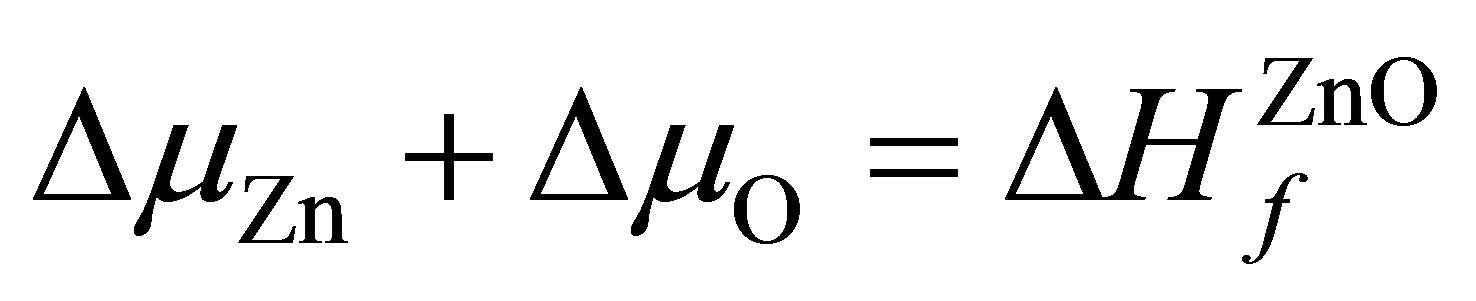(3)

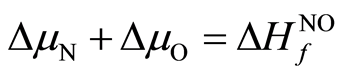(4)

其中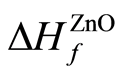，分别为ZnO，NO的形成熵。

如图3所示，从图中形成能的变化趋势可以看到，N原子在第一层位置(1/0/0)时的形成能最高，随着掺入到第二层、第三层时，形成能逐渐降低。这说明，N原子更容易掺到表面内部。然而，这与N掺杂ZnO体材料相比，N掺杂块体ZnO的形成能比掺入第二层时的形成能更低。因此，我们可以认为N原子更容易掺杂到ZnO内部，也就是容易占据体内位置，其次是掺杂到表面。

3.3. 电子结构

为了更细致分析其掺杂机制，我们计算了N掺杂表面的电子结构。如图4所示为ZnO (100)面总态

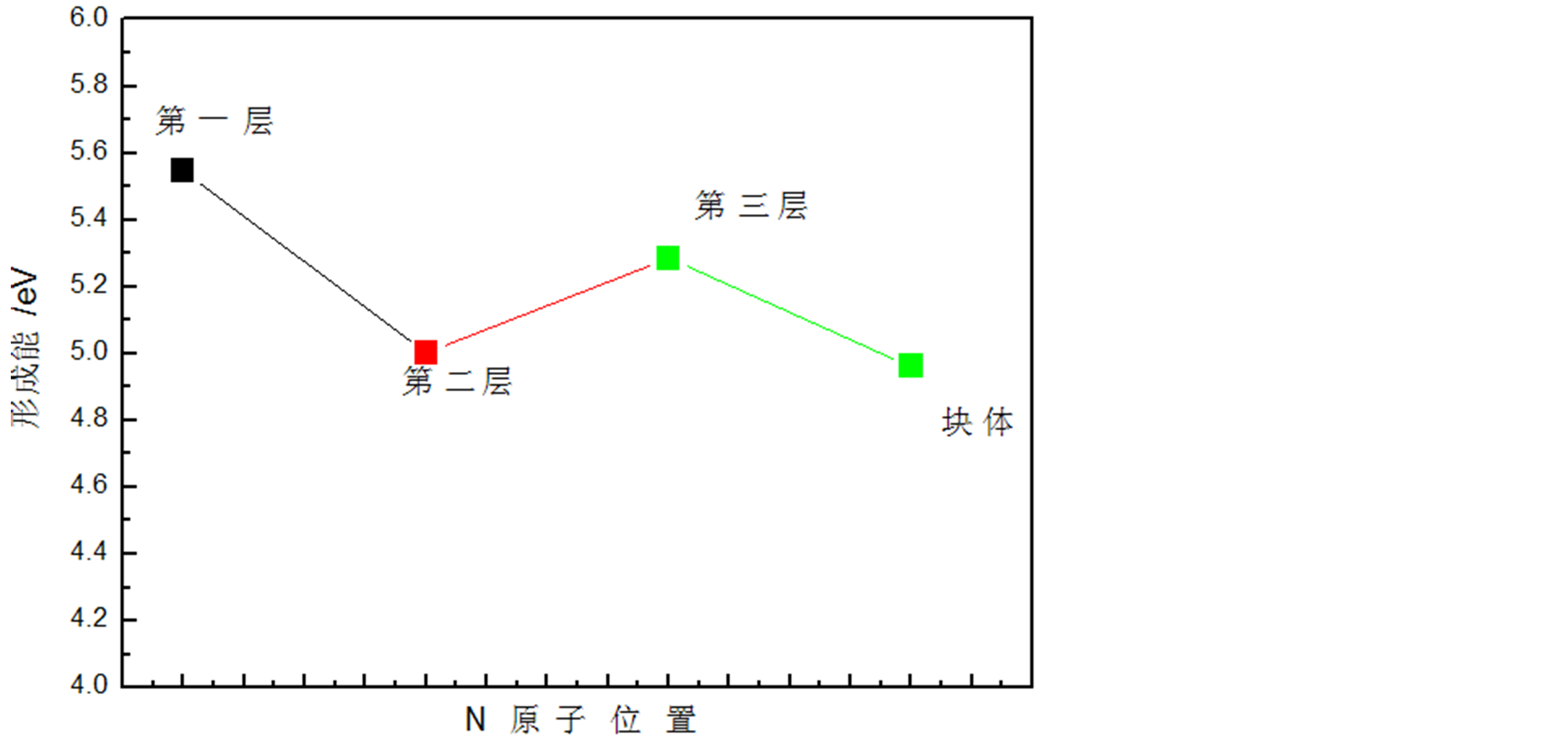
Figure 3. (Color Online) The formation energy of N doping ZnO (100) surface

图3. N掺杂ZnO (100)表面的形成能

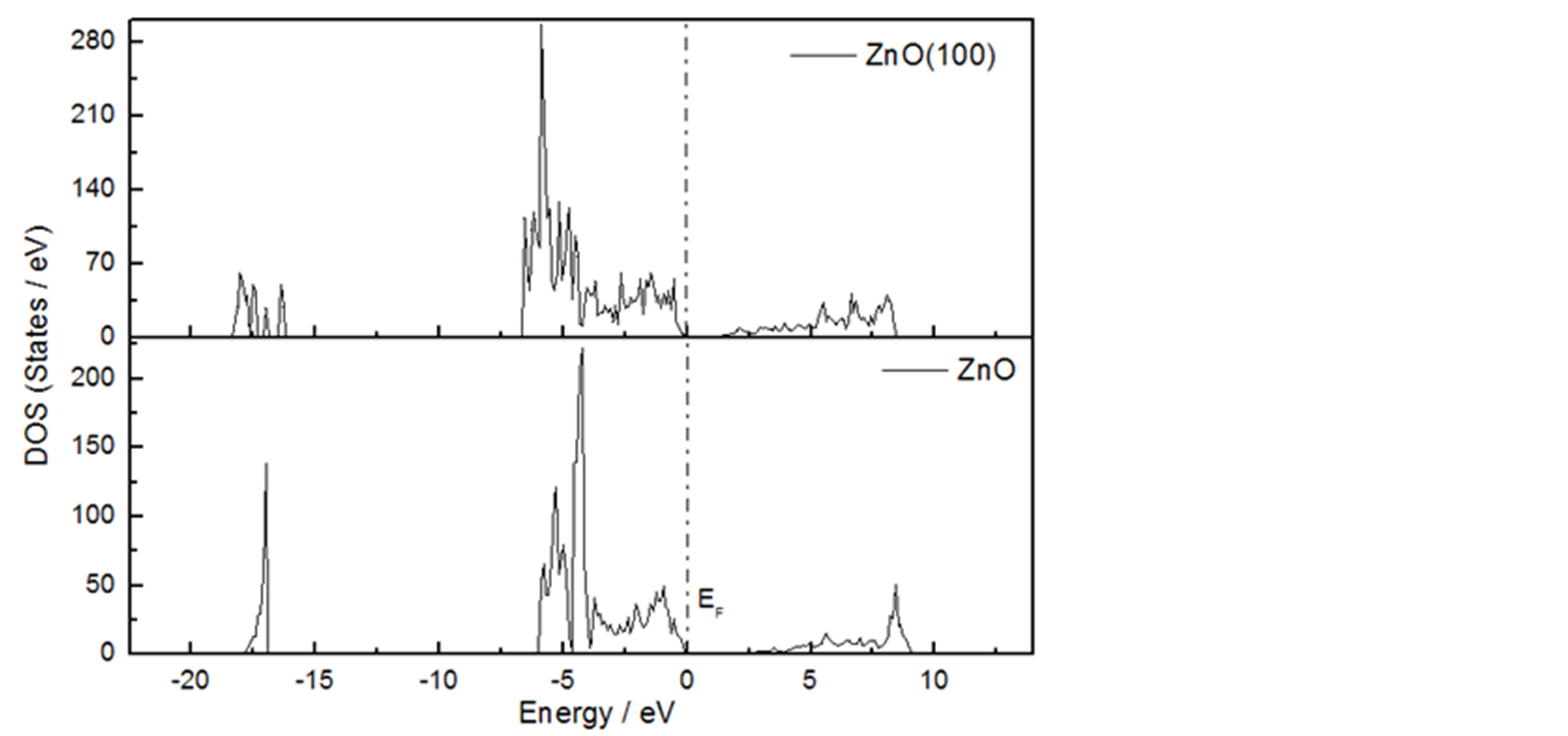
Figure 4. (Color Online) Total density of states of pure ZnO (100) surface and bulk ZnO

图4. ZnO表面层的总态密度和块体的态密度

密度图和块体材料ZnO的总态密度图的比较。对于ZnO (100)面，态密度图中存在明显的表面态。从分波态密度图5中我们可以发现，价带顶主要有O-2p态电子贡献，导带低主要由Zn-4s和O-2p贡献。表面层(suface layer)的O原子2p态电子向价带顶移动，在表面形成成键态的表面态；而Zn原子的4s态电子向导带底移动，在表面处形成反键态的表面态，从而导致ZnO(100)表面的带隙变窄，这是与块体材料的态密度图不同之处。

接着计算了N掺入不同层时的总的态密度和分波态密度。如图6所示。对于(1/0/0)表面的总态密度，和图4相比，费米能级进入价带，表现为p-型特征。并且导带向低能方向移动。从(0/1/0)表面的总态密度图中，我们发现费米能级同样进入价带，p型特征更加明显，表现为更明显的表面态。

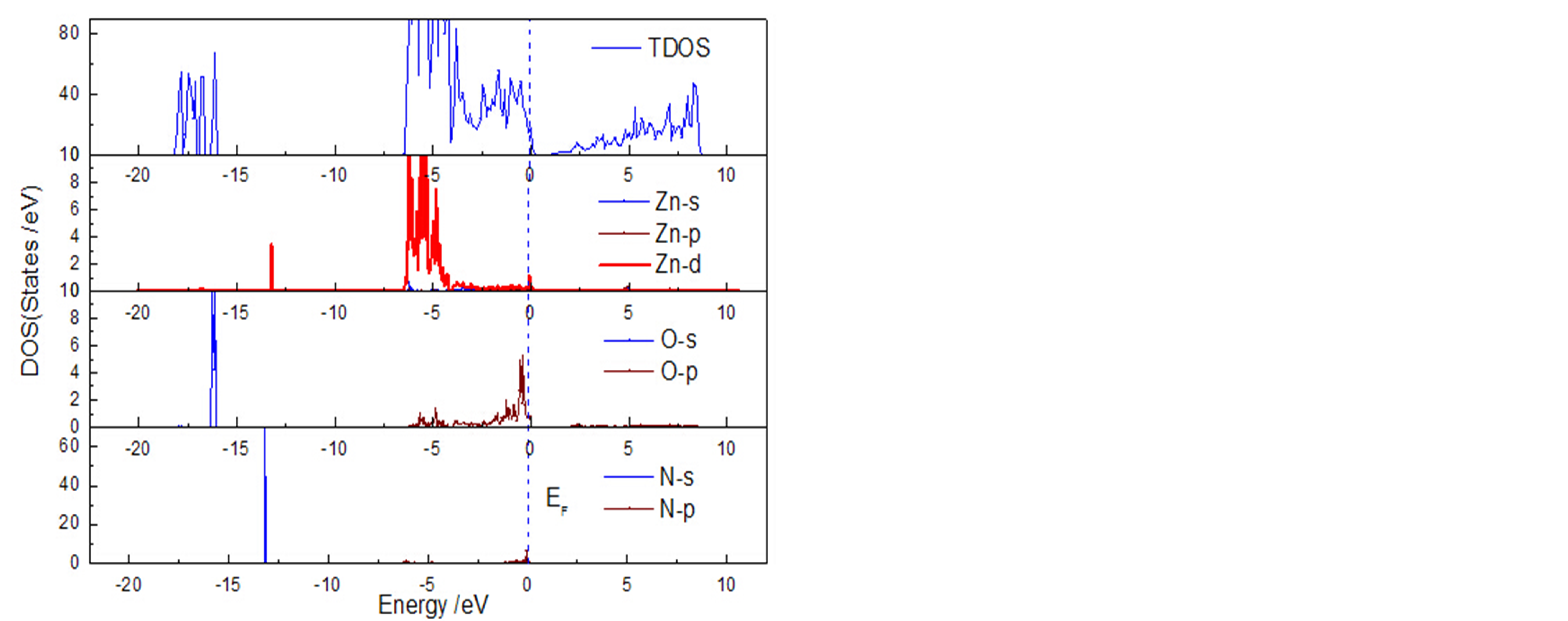
如图6(a)所示，在上价带(−8 eV~−0.5 eV)，主要由O-p态和Zn-d态贡献；下价带分两部分，一部分

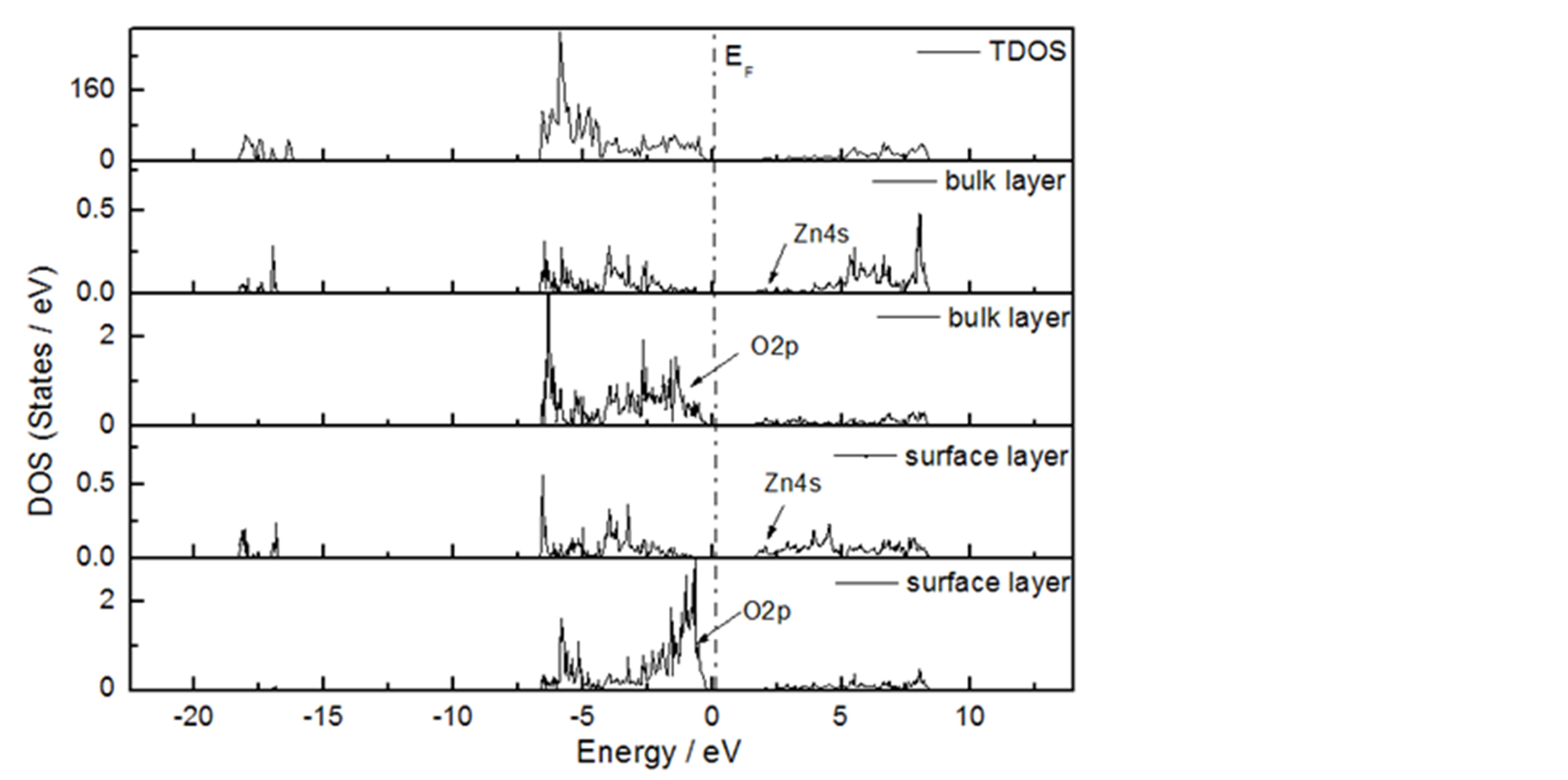
Figure 5. (Color Online) Density of states of surface layer and bulk ZnO

图5. ZnO表面层的态密度和块体的态密度

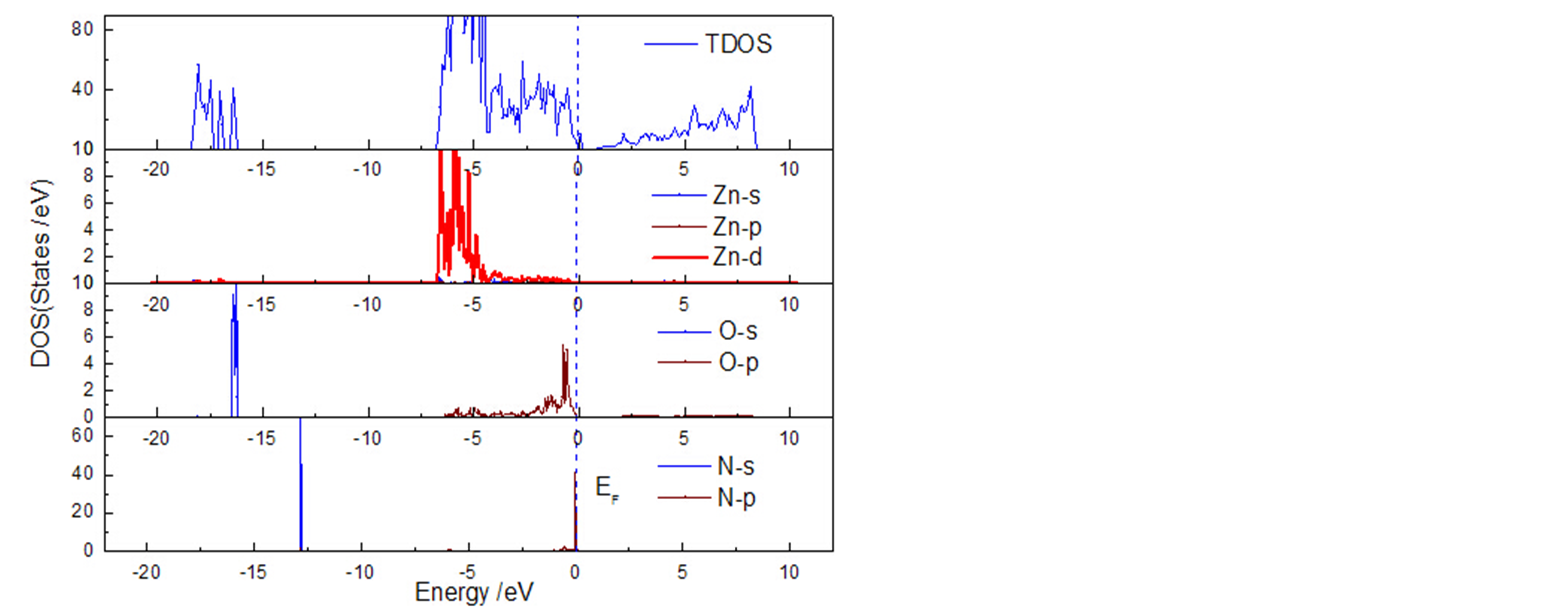(a)(b)

Figure 6. (Color Online) (a) The partial density of state of (1/0/0) surface, and (b) (0/1/0)

图6. (1/0/0)和(0/1/0)表面的电子结构

是(−15 eV~−10 eV)主要由N-s态决定；而下价带(−20 eV~−15 eV)主要由O-s态贡献。对于导带部分主要由Zn-d电子贡献，需要特别强调的是，在pure的ZnO (100)表面中，体系表现为本征态。而当N掺入到ZnO (100)表面时，在费米能级附近，主要由N-p电子提供。也就是，p-型特征主要由N原子贡献。当N掺入到表面第一层时，体系表现为p-型特征。

图6(b)为N掺入到第二层时的分波态密度图(也就是(0/1/0)表面)。从图中，我们发现每部分的基本贡献情况和(1/0/0)表面相似，不同的是，在费米能级附近，费米能级进入价带的程度相对要深，这与N掺杂ZnO (100)表面时第二层的形成相对要低相自洽。

致  谢

感谢江西科技师范大学江西省光电子与通信重点实验室计算中心的支持。

基金项目

国家自然科学基金(Nos. 51062003, 61264005)。

参考文献

[1] Qiu, Y.F., Fan, H.B., et al. (2014) Effect of nitrogen doping on the photo-catalytic properties of nitrogen doped ZnO tetrapods. Materials Letters, 131, 64-66.
[2] Zeng, Y.J., Ye, Z.Z., Xu, W.Z., Li, D.Y., Lu, J.G., Zhu, L.P. and Zhao, B.H. (2006) Dopant source choice for formation of p-type ZnO:Li acceptor. Applied Physics Letters, 88, 062107.
[3] Li, Q., Fan, G.H., et al. (2010) First-principles calculations of ZnO polar surfaces and N adsorption mechanism. Acta Physica Sinica, 59, 4170-4108.
[4] Xu, W.Z., Ye, Z.Z., Zeng, Y.J., Zhu, L.P., Zhao, B.H., Jiang, L., Lu, J.G., He, H.P. and Zhang, S.B. (2006) ZnO light-emitting diode grown by plasma-assisted metal organic chemical vapor deposition. Applied Physics Letters, 88, 173506-173513.
[5] Zhu, X.M., Wu, H.-Z., et al. (2010) Photoluminescence and resonant Ranab scattering in N-doped ZnO thin films. Optics Communications, 283, 2695-2699.
[6] Rajbongshi, B.M., Ramchiary, A. and Samdarshi, S.K. (2014) Influence of N-doping on photocatalytic activity of ZnO nanoparticles under visible light irradiation. Materials Letters, 134, 111-114.
[7] Zeng, Y.J., Ye, Z.Z., et al. (2007) Study on the Hall-effect and photoluminescence of N-dope p-type ZnO thin films. Materials Letters, 61, 41-44.
[8] Tuzemen, E.S., Kara, K., Elagoz, S., et al. (2014) Structural and electrical properties of nitrogen-doped ZnO thin films. Applied Surface Science, 28.
[9] Kresse, G. and Hafner, J. (1994) Ab initio molecular dynamics for liquid metals. Physical Review B, 47, 558.
[10] Kresse, G. and Furthermuller, J. (1996) Efficiency of ab-initio total energy calculations using a plane-wave basis set. Physical Review B, 54, 11169.
[11] 陈兰丽 (2011) 高p型导电率氧化锌的设计与计算. 硕士学位论文, 江西科技师范学院, 南昌.
[12] Lee, C.J., Lee, T.J., Lyu, S.C., Zhang, Y., Ruh, H. and Lee, H.J. (2002) Field emission from well aligned zinc oxide nanowires grown at low temperature. Applied Physics Letters, 81, 3648.

为你推荐