1. 引言
随机共振的概念是由Benzi等[1] 和Nicolis等[2] 在研究第四纪全球气象冰川问题时提出的。不同于通常人们对噪声的直观认识，由于随机共振现象体现了噪声的积极作用，因而引起了人们极大的兴趣。1983年，Fauve [3] 第一次在Schmitt触发器电路系统的实验中发现了随机共振现象的存在，并把信噪比的概念引入到随机共振的研究。后来，McNamera和Wiesenfeld等[4] 发展了绝热近似理论，得到了信噪比的解析表达式。此后随机共振在很多学科领域中得到了广泛的研究和初步应用，领域涵盖了物理、通信、光学、生物、神经网络等，并获得了丰硕的成果。
逻辑增长模型是细菌细胞增长和肿瘤细胞增长的一个基本模型，[5] [6] 研究了色噪声驱动下细菌增长系统的随机共振现象，结果表明噪声能够引起随机共振，在细菌的控制和治疗中具有一定的实际意义。本文研究了色噪声驱动下肿瘤细胞增长系统的随机共振现象，运用绝热近似理论和统一色噪声近似理论，获得了信噪比的表达式，并用数值模拟曲线分析了各参数对随机共振的影响，据此可以控制系统参数和噪声参数，使周期激励的治疗效果更好。
2. 肿瘤细胞增长系统的信噪比
肿瘤细胞增长模型为[7]
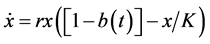(1)
其中x是肿瘤细胞群，r是增长率，K是承载能力，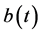
是周期函数，表示对肿瘤细胞群的周期激励作用. (图1)如果
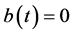，表示没有激励，平衡点是K；如果
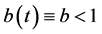，那么平衡点是
。相反，若
，则平衡点为0。如果对所有的t，
是正数，那么肿瘤细胞的增长率减小，且平衡点在0和K之间；反之，若
对某一t是负数，则肿瘤细胞群有一个负的增长率，肿瘤细胞被杀死，最终有一个零平衡。这里我们选择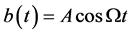
，A为振幅，
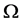是周期作用的频率，再考虑环境的影响
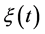(包括温度、PH值和离子强度等)，这样方程(1)改写为
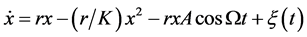(2)
这里
是指数型的高斯色噪声，具有如下统计性质
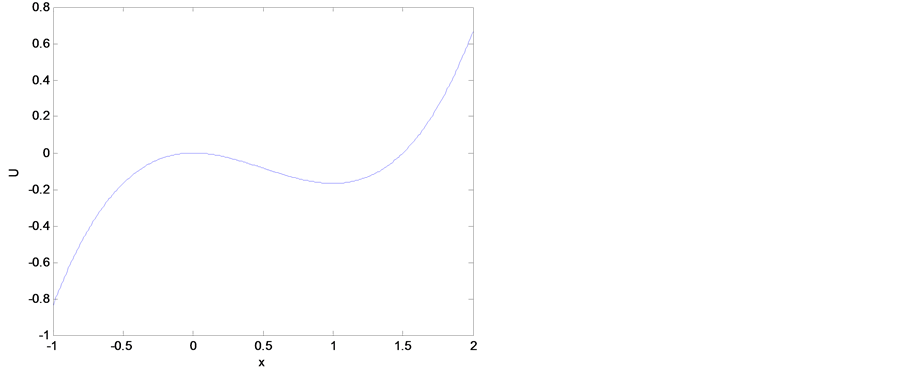
Figure 1. Potential function of the tumor cell growth system as r = K = 1
图1. 当r = K = 1时，肿瘤细胞增长系统的势函数
(3)
其中D是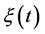
的强度，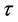
是其相关时间。方程(2)的势函数为
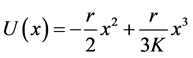(4)
当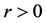
时，有一个不稳定点
和一个稳定点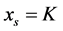
。反之，当
时，有一个稳定点
和一个不稳定点
。
根据Novikov定理[8] 和统一色噪声近似理论[9] ，方程(2)相应的FPK方程为
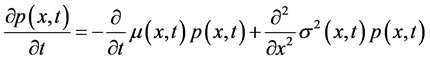(5)
其中
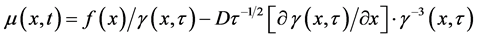
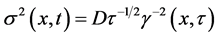(6)
由式(5)和式(6)，可解得其稳态概率密度函数为
(7)
这里C为归一化常数，
(8)
这里我们仅就
的情况讨论，
时的情况与此类似。利用平均首通时间的定义和文献，从稳定状态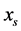
出发到达不稳定状态
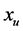的平均首通时间表达式为
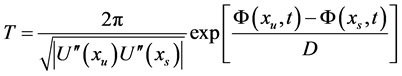(9)
上式成立要求
，即势垒高度远远大于噪声的强度D。从而得到克莱斯勒逃逸速率
(10)
根据McNamara和Wiesenfeld提出的绝热近似条件下的信噪比理论，得到方程(2)的输出总信号功率和信噪比表达式为
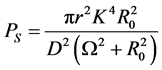(11)
(12)
其中
。
当A»1时，式(11)的括号中第二项可略去，则有
(13)
这就是方程(2)在绝热近似条件下的输出信噪比表达式。
3. 数值结果
为考察随机共振产生与否，我们借助于数值图像来讨论噪声强度对输出总信号功率的影响。图2给出了输出总信号功率P随噪声强度D变化的函数关系，在小D时，增加噪声强度十分有效地提高了输出总信号功率，即产生了共振，说明在一定范围内，适当的增加噪声强度有助于提高周期激励的治疗效果。
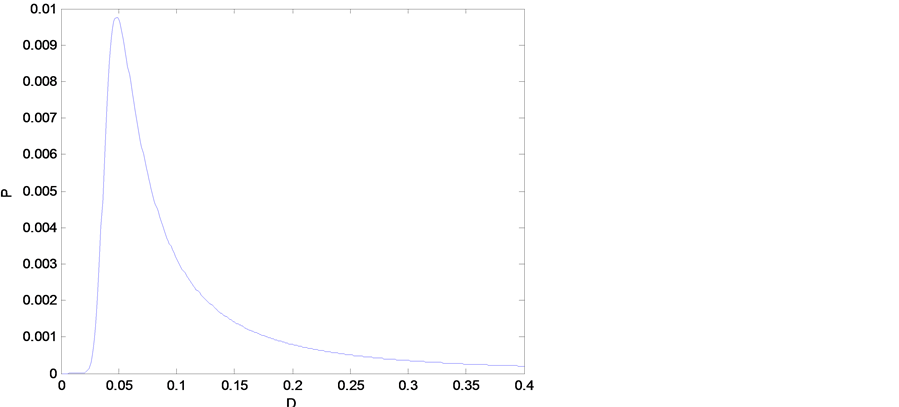
Figure 2. The relationship between total power of output signal and noise intensity (r = K = 1, A = Ω = 0.01)
图2. 输出信号总功率与噪声强度的关系(r = K = 1, A = Ω = 0.01)
式(13)给出了信噪比的解析表达式，下面在满足绝热近似的条件下，讨论不同参数对信噪比的影响。
图3描述了不同增长率下，信噪比随噪声强度变化的函数关系。从图中可以看到，随着噪声强度的变化，信噪比曲线出现了单峰，产生了随机共振。共振峰随着增长率r的增加而增大，说明r越大，随机共振强度越大。同时共振峰随着r的增加而向右移动，说明增长率越大，要达到随机共振所需要的噪声强度也在增加，这与实际是符合的。因此通过调节噪声强度D可以控制随机共振。
图4显示了信噪比作为噪声强度的函数随承载能力K变化的曲线。同样，随着噪声强度的增加，信噪比曲线出现了单峰，产生随机共振。随着承载能力K的增强，共振峰向右移动，表明承载能力越强，
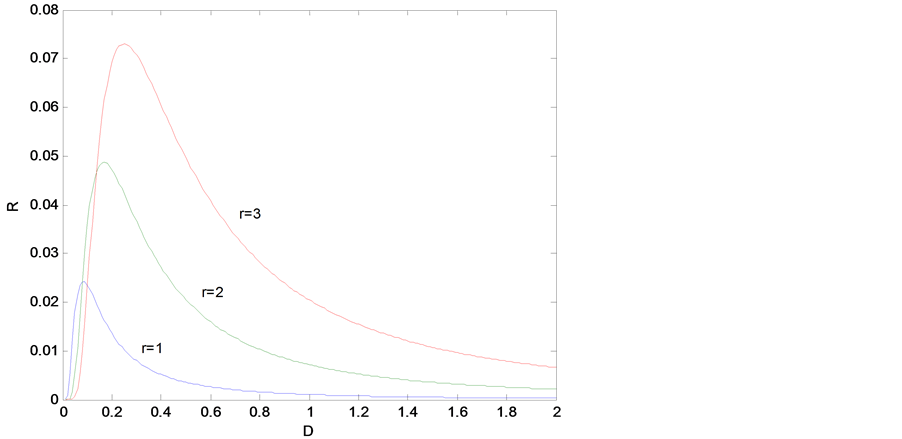
Figure 3. Vary of signal-to-noise ratio as a function of noise intensity with growth ratio r (A = 0.1, K = 1)
图3. 信噪比作为噪声强度的函数随增长率的变化(A = 0.1, K = 1)
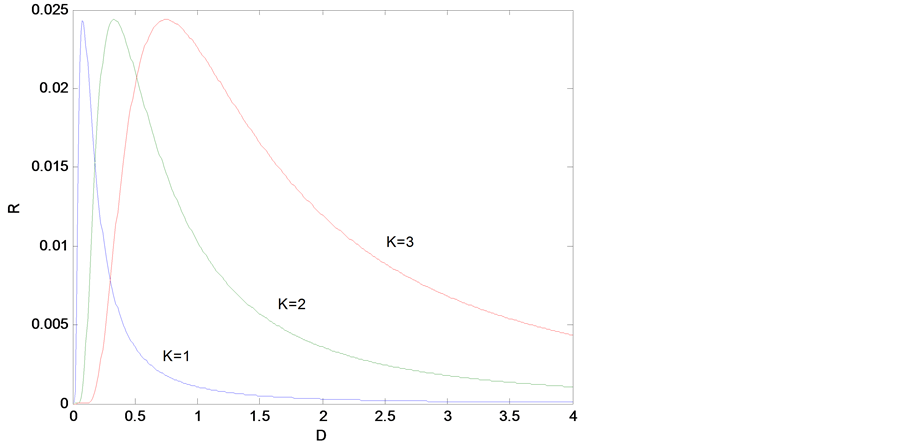
Figure 4. Vary of signal-to-noise ratio as a function of noise intensity with carrying capacity K (r = 1, A = 1)
图4. 信噪比作为噪声强度的函数随承载能力的变化曲线(r = 1, A = 1)
要达到随机共振所需要的噪声强度也越强。但是承载能力K对峰值没有显著影响，即对随机共振的强度没有显著影响。
图5描述了信噪比作为噪声强度的函数随着激励振幅的变化的情况，表明激励强度越大，发生随机共振的强度也越大，但这种共振受噪声强度的影响不显著，都是在
时达到了共振。同时从图6看
Figure 5. Vary of signal-to-noise ratio as a function of noise intensity with periodic excitation amplitude A (r = K = 1)
图5. 信噪比作为噪声强度的函数随振幅的变化曲线(r = K = 1)
Figure 6. Vary of signal-to-noise ratio as a function of noise intensity with periodic excitation frequency (r = K = 1, A = 0.01)
图6. 信噪比作为噪声强度的函数随频率的变化曲线(r = K = 1, A = 0.01)
到，信噪比作为噪声强度的函数随频率变化的三条曲线几乎是重合的，说明随机共振几乎不受激励频率的影响。
4. 结论
本文研究了色噪声和周期治疗驱动下肿瘤细胞增长系统的随机共振。结果表明，在噪声强度较小时产生了随机共振，并且随机共振也受到系统中各参数的影响。随机共振的强度随着增长率和周期激励振幅的增加而增加，而承载能力和周期激励的频率对随机共振的强度没有显著影响。因此我们可以通过调节噪声强度、增长率和周期激励振幅来控制随机共振，以达到更好的治疗效果。