1. 引言
分数阶微分和积分于1832年出现在Liouville的位势方程中，1881年又出现在Abel的等时降落线问题中 [1] [2] ，此后在物理、生物、化学等多个学科领域都得到了广泛的应用。近30年来，分数阶微分和积分已被应用到分数回归模型 [2] ，粘弹性力学 [3] 、控制系统与控制器 [2] 、电子回路 [4] 、电分析化学 [5] 、生物系统的电传导 [6] 、神经分数模型 [7] 等方面。目前，分数阶微分方程已成为数学和物理学相关分支领域的研究热点。分数阶Schrödinger方程就是一个被许多学者研究过的典型偏微分方程，例如，文献 [8] 研究了时间分数阶线性Schrödingerr方程，空间分数阶线性Schrödinger方程和时空分数阶线性Schrödinger方程，给出了它们在不同势下的解形式。 [9] - [11] 分别用分数阶变分原理和Klein-Gordon方法、Crank-Nicholson方法、Feynman-Kac公式和Markov特性得到空间分数阶线性Schrödinger方程和它在无限远处的本征解、稳定性和收敛性等。 [12] [13] 分别应用翻山原理和Ekeland变分原理、动量表象法研究了空间分数阶非线性Schrödinger方程解的多重性和精确解。 [14] 研究了N维空间上分数阶非线性Schrödinger方程的基态解。 [15] 用Profile分解法得到了空间分数阶非线性Schrödinger方程的驻波解的轨道稳定性和基态解的不稳定性。
李群对称约化是一种可将偏微分方程直接约化为常微分方程的有效方法，通过求解约化方程得到原偏微分方程相似解、解析解和精确解。同时，利用方程的李对称群还可以由方程的已知解去构造方程的新解 [16] 。李群对称约化应用于分数阶偏微分方程的研究有一些结果，例如，于兴江等利用李群约化方法把Boussineq方程约化为Erdelyi-Kobe分数阶常微分方程 [17] ；Guo-cheng Wu应用李群约化法得到了时空分数阶Diffusion方程的一些新解 [18] ；杨绍杰利用李群约化方法得到了时间分数阶KdV方程和耦合KdV方程组的约化方程和一类孤立波相似解 [19] 。
综上所述，目前还没有将李群约化方法应用于分数阶非线性Schrödinger方程的研究。因此，在本文中，我们的主要目的就是将李群约化方法应用到一类空间分数阶非线性Schrödinger方程，结果是得到了它的依赖于单参数的衍生解和约化方程，并通过求解约化方程得到空间分数阶非线性Schrödinger方程的群不变解和孤立波解。
2. 一类空间分数阶非线性Schrödinger方程的李对称分析
在本节中，我们将应用李群方法 [20] [21] 研究一类空间分数阶非线性Schrödinger方程，获得它的无穷小生成元和李代数换位子表，以及与每一个生成元相对应的李对称群，再进一步通过李对称群和方程的已知解衍生出了方程的新解。
2.1. 一类空间分数阶非线性Schrödinger方程的引入
2002年，Laskin在他的著作“Fractional Schrődinger Equation” [22] 中给出了如下一类空间分数阶Schrödinger方程：
(1)
其中
，
为非相对论量子体系中的特征速度，且
具有如下量纲：
；
是势函数；
是如下的量子Riesz分数阶导数：
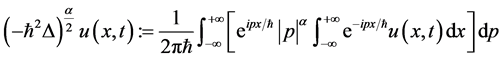
1997年，Saichev A和Zaslavsky G.M.在他们的著作“Fractional Kinetic Equations: Solutions and Applications” [23] 中将分数阶的拉普拉斯算子表示为：
(2)
如将(2)式代入方程(1)中，则可得到如下形式的空间分数阶Schrődinger方程：
(3)
在文献 [24] 中给出了Caputo分数阶导数定义下的非线性时空分数阶Schrődinger方程：
(4)
对于量子Riesz分数阶导数定义下的空间分数阶非线性Schrődinger方程，在应用李群约化方法下很难找到它的单参数李群变换。如果将方程(4)中的非线性项改为任意常数，我们发现仍不能得到它的无穷小生成元和单参数李群，这样就给后面的求解带来极大困难。因此，为能够获得空间分数阶非线性Schrődinger方程的单参数李群变换，并顺利求出相关的解。本文中将主要研究如下的一类空间分数阶非线性Schrödinger方程：
, 
(5)
其中的分数阶导数采用Caputo定义：
(6)
在本文后面关于不变群生成元及约化方程的计算中，将用到分数阶导数的如下几个性质：
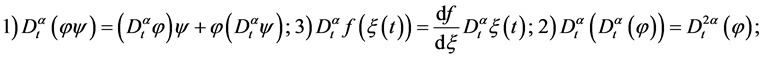
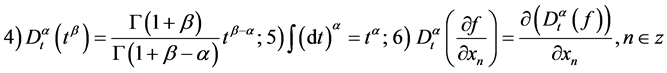
2.2. 方程(5)的李代数、李对称群及其单参数解
为得到方程(5)的李对称群和衍生解，我们假设方程(5)的不变群生成元为：
(7)
其中：
为相应的无穷小量，
与
互为共轭。
设单参数的李群变换为：
(8)
则不变生成元(7)的分数的二阶延拓为：
(9)
利用如下不变性条件：
，
(10)
我们有：
(11)
其中
表示全导数。
(12)
将(12)代入(11)中，且令
(其中
；
；
；
)等项的系数为零，则得到如下的分数阶偏微分方程组：
(13)
借助于Maple软件编程计算，可得方程组(13)的如下一组解：
(14)
其中
是任意常数。
于是，由解组(14)我们得到方程(5)的不变生成元的一个4维的李代数，它的一组基为：
(15)
因此，我们有如表1所示的
间的换位子。
表1.
间的换位子
由于表1的换位子表并不完备，故我们只可以由上述生成元得到的单参数不变群衍生出方程(5)的部分依赖于一个单参数的新解。
下面，我们先给出由生成元
得到的单参数不变群：
(16)
现假设
是方程(5)的解，则以下的
都是方程(5)的解：
(17)
(18)
(19)
(20)
连续利用不变群(16)，则可由方程(5)的已知解
生成如下新解：
(21)
2.3. 空间分数阶非线性Schrödinger方程的李对称约化
在这里，我们将利用2.2节中得到的不变生成元(15)和分数阶特征方法 [20] [25] ，在5种情形下分别给出方程(5)的李对称约化方程，进而求出方程(5)的群不变解。
情形1：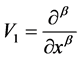
的分数阶特征方程为：
(22)
由方程(22)可以得到如下不变量：
(23)
将不变量(23)代入方程(5)便可得到如下约化方程：
(24)
由于群不变解
是一个复函数，故我们假设：
(25)
其中
是
的实函数。将(25)式代入方程(24)中，可得到如下方程组：
(26)
解方程组(26)得到约化方程(24)的解为：
(27)
于是，我们得到方程(5)的群不变解为：
，
为任意常数 (28)
情形2：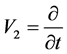
的分数阶特征方程为：
(29)
由方程(29)可以得到如下不变量：
(30)
将不变量(30)代入方程(5)便可得到如下的约化方程：
(31)
将(25)式代入方程(31)中，可得到如下的方程组：
(32)
解方程组(32)得到约化方程(31)的解为：
(33)
于是，我们得到方程(5)的群不变解为：
(34)
其中
为任意常数。
情形3：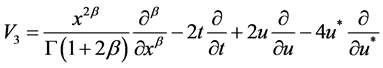
的分数阶特征方程为：
(35)
由方程(35)可以得到如下不变量：
(36)
将不变量(36)代入方程(5)可得到如下的约化方程：
(37)
将(25)式代入方程(37)中，可得到如下的方程组：
(38)
解方程组(38)，我们得到约化方程(37)的解为：
(39)
从而得到方程(5)的如下群不变解：
(40)
其中：
为任意常数，且
，
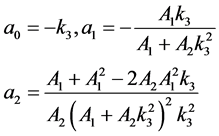
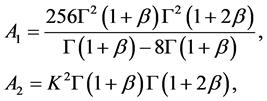
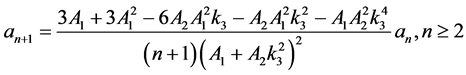
情形4：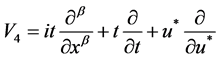
的分数阶特征方程为：
(41)
由方程(41)可以得到如下不变量：
(42)
将不变量(42)代入方程(5)便可得到如下的约化方程：
(43)
由于方程(43)中的变量
不能用
替换，故我们得不到它的解，因而也就得不到(5)的群不变解。
情形5：
，其中
为非零常数。
的分数阶特征方程为：
(44)
由方程(44)可以得到如下不变量：
(45)
将不变量(45)代入方程(5)可得到如下的约化方程：
(46)
将(25)式代入方程(46)中，可得到如下的方程组：
，其中
(47)
解方程组(47)，我们得到约化方程(46)的解为：
(48)
其中
，
为任意常数。
如令
，则可得到方程(5)的如下行波解：
，
(49)
3. 结论
本文将李群约化方法应用到空间分数阶非线性Schrödinger方程(5)，得到的主要结论如下：
利用方程(5)的一个已知解，由方程(5)的单参数不变群衍生出方程(5)的单参数的解，它满足(21)；由方程(5)的不变生成元，通过解方程(5)的约化方程得到了方程(5)的群不变解，例如：(28)、(34)、(40)；在2.2节中，我们利用不变生成元
得到了方程(5)的行波解(49)。
关于李群约化方法应用到其他形式的分数阶非线性Schrödinger方程，我们将另文讨论。
基金项目
本文由国家自然基金项目(11162020)资助。