双层复合管流固耦合振动的动力特性分析

Dynamic Characteristics of Fluid-Structure Interaction Vibration in Double Layer Pipe

摘要: 基于复合材料力学层合板的并联和串联模型，将双层复合管等效简化为单层管，在此基础上对空管分别进行了理论计算、数值模拟和实验研究，验证了模型的有效性；对于充液复合管的流固耦合系统进行等效简化，然后应用行波法计算其固有频率，并与数值模拟和实验结果进行了对比，证实了行波法简洁且有效；最后采用行波法讨论了双层复合管中材料和尺寸的变化对结构固有频率的影响。研究结果表明，并联简化模型较适用于含有金属材料的管道，而串联模型适用于非金属材料管道；行波法计算方便快捷，宜于编程实现，且计算结果与已有成果吻合良好。

Abstract: Based on the parallel and the serial model for laminated plates of composite material mechanics, the double layer pipe is equivalent simplified as single pipe. On this basis, the respectively theo-retical calculation, numerical simulation and experiment research about the empty pipe proof the effectiveness of this model. The natural frequencies of fluid-solid coupling system of liquid filled composite pipe are calculated by using the traveling wave method, and the results are made comparison between the results of numerical simulation and experiments; they confirm the conciseness and effectiveness of the traveling wave method. Finally the influence of the material and size in double layer composite pipe on the natural frequency of the structure is discussed by the traveling wave method. The results show that the parallel simplified model is more suitable for the metal pipes while the serial model is more suitable for the metalloid pipes; the traveling wave method is clear for problem-solving, suitable for programming, and the calculation results are consistent with the existing results.

1. 引言

输液管道的流固耦合振动问题广泛存在于航天航空、核工业和石油化工等领域。众多研究者从不同的方面对这一问题进行了研究。对输流管中流固耦合问题进行研究时，大多研究者采用特征线 [1] 、有限元 [2] 等方法，但对于同一模型，这些方法由于存在插值问题，因此带来较大的数值误差，严重影响到预测的精度。近年来应用较多的传递矩阵法 [3] [4] ，对具有链式结构的管道系统较为方便，但要应用到复杂形状的管系，则有一定困难。行波法 [5] [6] 则是以振动波在输水管路系统中的传播和反射为基础来建立并分析水泵、阀门、水锤防护设备等泵站管路系统元件的数学模拟，具有概念清晰、简洁、形象而且直观的优点，与计算求解步骤繁琐抽象的特征线法相比，易于掌握和应用。目前涉及输流管中的流固耦合问题绝大部分工作都是围绕单层管进行的，对多层管的研究较少。

复合管 [7] - [9] 是由两种(或多种)具有各自特性的单体管通过特定的工艺手段把它们结合成一体，从而使它具有综合特性的价廉物美的新型管。复合管既有很高的强度，又有很好的耐腐蚀性能、耐磨性能以及其他特殊性能，工程中可通过选择合适的材料进行匹配来满足各种特殊使用场合，同时，复合管还节约材料，节省投资。因此复合管作为一种新型结构管材，在石油、化工、造船、能源、航天等工业部门得到广泛应用。那么，对复合管的流固耦合问题进行研究，找出其与普通单管管路的区别，形成系统的复合管研究体系，有效的避免双层管路的共振区域，对复合管的普及应用，工程应用具有重要的理论意义和工程实际价值。S. Yoshikawa [10] 等人从理论和实验两方面研究了两个无限长同心圆柱壳的流固耦合振动问题。陈美霞 [11] 等人建立了无限流体中的有限长单双层加肋圆柱壳模型，并对单、双层圆柱壳体以及双层圆柱壳体内、外壳的振动响应性能作了一定的比较，壳体的振动用Fhigge壳体方程描述，将加强构件等价为对内外壳体的支持力，最后求解双壳体声–流体–结构耦合方程。张慧玲 [12] 用二维线弹性平面应变理论，对双层复合筒、多层复合筒、双层碳纳米管和多层碳纳米管中周向导波的传播，进行了理论和数值研究，讨论了固体与固体接触面的界面特性对周向导波的影响。

本文运用复合材料力学层合板的分析方法，将双层复合管等效简化为单层管。分别对空管和充液管进行了理论计算、数值模拟和实验研究，从而验证了简化模型的可行性和行波法的有效性。

2. 双层复合管的等效简化

2.1. 双层复合管的简化模型

双层管由于两种材料参数不同以及内外管间的界面条件影响，不能直接按单层管理论求解。本文研究的双层复合管，假设两层材料均属宏观均质材料，在使用条件下不发生脱离，故参照复合材料力学的分析方法，在假设应变连续和应力连续基础上，将双层管等效简化为单层管。

图1所示为双层管轴向剖面图。其中，E₁、E₂分别为内外层材料的弹性模量，ρ₁、ρ₂分别为内外层材料的密度，d₀、d₁、d₂分别为管道内径，内层材料外径，管道外径。

密度拟合根据总体积当量按下式计算：

(1)

式中：M——管道总质量，V——管道总体积，r为等效密度。

参照复合材料力学 [13] 中研究层合板的方法对双层管的弹性模量E进行等效拟合。复合板模型有两种方法如图2所示，并联法和串联法。

对并联模型有：

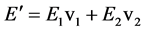
式中：E'为并联模型拟合弹性模量，v₁为内层材料体积份额，v₂为外层材料体积份额。

对串联模型有：

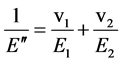
式中：为串联模型拟合弹性模量。

分别计算两种模型的体积份额，得到并、串联两种模型下的等效弹性模量计算式如下：

(2)

(3)

2.2. 理论计算

取一段空心管如图3，根据振动理论，按空心等截面悬臂梁计算其固有频率 [14] ，得到下式：

(4)

式中：w_i——管道第i阶固有频率/rad∙s⁻¹，l——管长，EJ——管道横截面的抗弯刚度，ρ——管道密度，A——梁的横截面积，前4个b值为：其中E，r均为等效拟合参数。

2.3. 数值模拟

有限元法建立双层复合管的动力学模型，可以选择实体单元对结构进行离散。管道内外层材料接触面设置为完全固接，模型左端设置为固定端，右端为自由端。图4和图5分别双层管和简化为单层管后的几何模型：

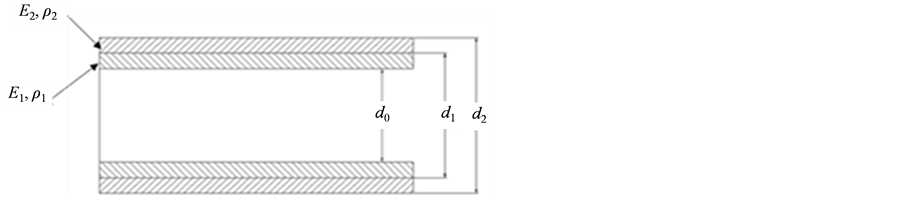
Figure 1. Axial section of double layer pipe

图1. 双层管轴向剖面图

Figure 2. Composite plate model

图2. 复合板模型

Figure 3. Hollow pipe model

图3. 空心管模型

Figure 4. Double layer pipe model

图4. 双层管模型

Figure 5. Simplified pipe model

图5. 简化模型

对管道进行网格划分，采用ANSYS软件进行固有频率计算。

2.4. 实验研究

分别取不锈钢–碳钢，塑料(PVC) –碳钢和纳米–塑料(PVC)三种复合管进行实验研究。三种研究对象的尺寸和材料参数分别如下：

图6为内衬不锈钢钢管，长84.5 cm，内径65 mm，外径89.5 mm，内层管道材料为304不锈钢，密度7930 kg/m³，弹性模量192 GPa，厚度3 mm。外层管道材料为普通碳钢，密度7850 kg/m³，弹性模量206 GPa，厚度9.25 mm。

图7为内衬PVC钢管，长1.3 m，内径38 mm，外径48 mm，内层管材为PVC，密度1370 kg/m³，弹性模量3.4 GPa，厚度2 mm，外层管材为碳钢，参数同上，厚度3 mm。

图8为内衬纳米塑料管，长86 cm，内径14 mm，外径20 mm，内层材料为碳纳米材料，密度1300 kg/m³，弹性模量1050 GPa，厚度0.5 mm，外层材料为PVC，参数同上，厚度2.5 mm。

搭建管道实验平台如图9所示(以内衬不锈钢钢管为例，其它图略)，将敲击实验采集到的三种管道的时域信号，通过傅立叶变换转化为频域信号，分别如图10、图11和图12。

2.5. 结果分析

将三种管道的理论计算、数值模拟和实验结果分别列在表1~3中。

内衬为不锈钢钢管的三种结果对比见表1。由于高频无法测出，实验结果只有1，2阶。从表中可以看出，管道内外层材料的弹性模量及密度相差不大，管道一阶固有频率，采用串、并联模型计算的理论结果与实验结果相近；串、并联模型数值模拟结果比实验结果和理论计算值略大；其他高阶频率规律类似。

内衬为PVC钢管的固有频率结果对比见表2。此时管道内外层材料的弹性模量及密度差别较大，两种简化模型的结果有明显的差异，串联模型的理论计算结果和数值模拟结果相比实验结果误差较大，而并联模型无论理论计算还是数值模拟与实验结果吻合较好。

表3为内衬纳米材料的PVC塑料管的固有频率值。从表中可看出，当内外两种材料弹性模量相差很大时，并联简化模型的结果无论数值模拟还是理论计算都与实验结果相差很大，而串联模型的结果与实验结果较为接近。

以上分析表明，内外层材料性能接近时，并、串联模型均能较好地等效模拟双层管；而材料性能相差较大时，需根据具体材料选择不同的简化模型。因实验数据有限，暂时难以给出定量的选择模型的标准，有待进一步的分析。

Figure 6. Stainless steel lined steel pipe

图6. 内衬不锈钢钢管

Figure 7. PVC lined steel pipe

图7. 内衬PVC钢管

Figure 8. Lined with nano-material plastic pipe

图8. 内衬纳米塑料管

Figure 9. Test bed for stainless steel lined steel pipe

图9. 不锈钢钢管实验台

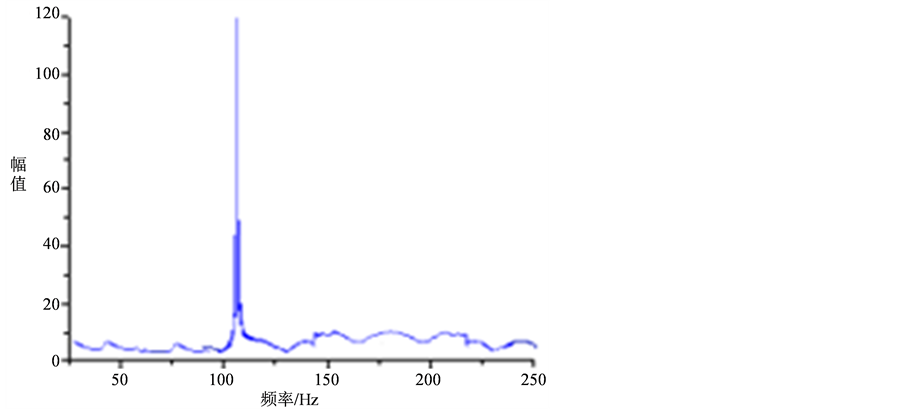
Figure 10. Frequency domain signal diagram for stainless steel lined steel pipe

图10. 内衬不锈钢钢管频域信号图

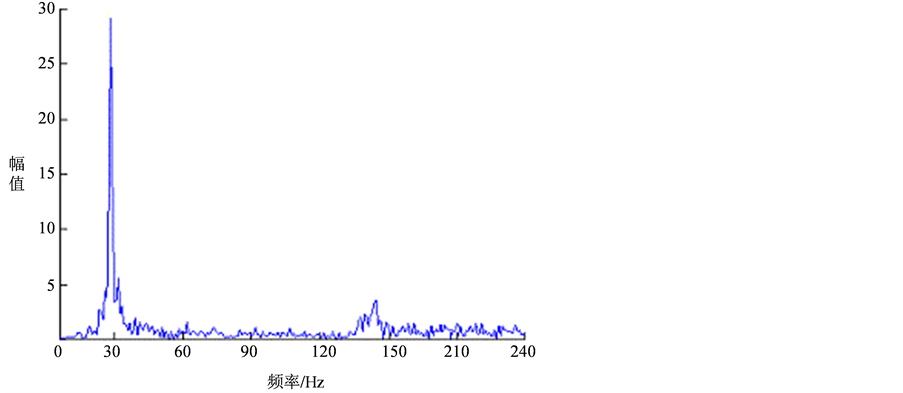
Figure 11. Frequency domain signal diagram for PVC lined steel pipe

图11. 内衬PVC钢管频域信号图

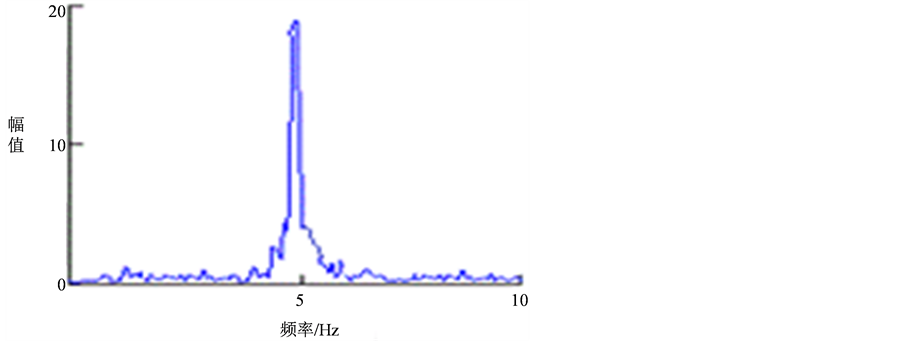
Figure 12. Frequency domain signal diagram for lined with nano- material plastic pipe

图12. 内衬纳米塑料管频域信号图

Table 1. Natural frequency of stainless steel lined steel pipe

表1. 内衬不锈钢钢管的固有频率

Table 2. Natural frequency of PVC lined steel pipe

表2. 内衬PVC钢管的固有频率

Table 3. Natural frequency of lined with nano-material plastic pipe

表3. 内衬纳米材料塑料管的固有频率

3. 充液复合管流固耦合振动的固有频率计算

3.1. 行波法

单层管考虑流固耦合的振动方程已建立 [15] 。取一段直管单元如图13所示，应用行波法来研究管道系统的流固耦合振动。

流固耦合轴向振动经典四方程为：

(5)

式中：u_z、v、p、f_z分别为管道轴向位移、流体流速、流体压力和管道轴向力；ρ、γ分别为材料的拟合密度和泊松比；E为材料的拟合弹性模量；A为截面面积；r、e分别为管内径和壁厚。K为流体体积模量，

，下标p和f分别表示管道与流体。令，代入(5)式，可得

(6)

式中：，为轴向振动的波幅系数，k_ai (i = 1, 2, 3, 4)，为管道轴向振动的波幅数。，，k_a1,2对应于左行波，k_a3,4对应于右行波。这里的，，

Figure 13. Straight pipe unit

图13. 直管单元

，

。，，

，，，，

，，。

流固耦合横向振动方程为：

(7)

式中：f_x为剪力，u_x为横向位移，m_y为弯矩，θ_y为转角，m为管道质量，EI_p为管道抗弯刚度，G为材料剪切模量。，I_p与I_f分别为管道与流体所对应圆截面的轴惯性矩，K_rf为弯曲修正因子，对直管道取1。同样对其中的参数r和G进行等效拟合。

令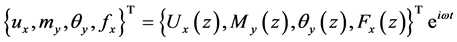

代入方程(7)，可以得到管道横向位移、弯矩、转角和剪力表达式，即

(8)

式中：，为横向振动的波幅系数，k_b1,2对应于左行波，k_b3,4对应于右行波。

，

，，，。

，，

，。

定义局部位移和力幅值位移向量：

，

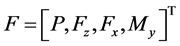
将式(6)和(8)中的方程按先左行波后右行波的方式重组，得到单元管道流固耦

合振动的波导方程：

(9)

式中：，。Y_uL，Y_uR，Y_fL，Y_fR为联系状态向量与波模式幅值的矩阵，W_L，W_R分别为左右波模式幅值向量。

根据单元波模型中入射波、反射波与单元左、右节点的传递关系，将式(9)代入相应的边界条件，对单元进行组装，即可得到系统自由振动的方程为

(10)

式中：，G、S为s、g单元组装后的矩阵，z_o，z_i为z₁，z₂组装后的矩阵。，。

其详细推导过程见文献 [16] 。当且仅当方程(10)有非凡解时，结构才能保持自由振动状态，即

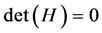
上式为系统特征方程，具有无穷多个解，对应于系统的无穷多个固有频率。

3.2. 数值模拟

ANSYS很早已开始进行流固耦合的研究和应用，文中分别使用双层管模型以及等效简化的单层管模型进行对比。

设置管道长度，内径，外径，内层材料厚度，管道支撑方式，管道材料，液体类型，管道内外层材料接触面设置为完全固接。在Geometry中，建立双层管道模型，如图14所示。

使用Fill功能，使液体充满管道，产生流体模型，如图15所示。

在进行单向流固耦合分析时，对管道结构进行抑制，对流体进行网格划分，如图16所示。

在WORKBENCH下选择FLUENT求解器，利用生成的网格进行求解设置。

设置流动模式，为标准的k-ε模型；选择不可压缩流体介质作为流体材料；入口条件及出口条件设为速度条件和压力条件。

求解后将流体计算结果直接传递给Static Structural，将几何模型也传递给Static Structural的Geometry，选择流体区域使用抑制功能，保留管道实体进行操作。对管道进行网格划分后，将流体数据加载给结构，对管道进行支撑设置，计算求解。

以内衬不锈钢钢管为例，分别用双层管模型和单层管模型计算充液管道流固耦合振动的固有频率，根据1.5中的结论，简化模型采用并联模型，结果见表4。

可以看出，简化模型结果与双层管模型结果吻合很好，说明简化模型对流固耦合问题同样有效，而且可以缩短计算时间，减少计算量。

取管道长度l = 2 m，两端简支，内层材料为不锈钢，厚5 mm，外层材料为碳钢，厚5 mm，管道内径6 cm，外径8 cm，两种材料的参数同1.4中。选取五种工况，分别用行波法求解和Ansys软件数值模拟，计算结果如表5。

由表5可以看出，五种工况下，管道一阶固有频率的最大误差为1.5%，管道五阶固有频率的最大误差为0.27%。说明使用行波法具有一定的准确度，且比ANSYS数值模拟快捷简便。

Figure 14. Double layer straight pipe model

图14. 双层直管模型

Figure 15. Liquid filled pipe model

图15. 充液直管模型

Figure 16. Liquid element mesh

图16. 流体单元网格划分

Table 4. Numerical simulation of stainless steel lined steel pipe

表4. 内衬不锈钢钢管数值模拟结果

Table 5. Comparison of traveling wave method and numerical simulation

表5. 行波法与数值结果对比

3.3. 实验研究

由于充液管道实验的实验条件的限制，本文只对内衬PVC钢管进行了充水实验，其尺寸和材料参数见1.4。管道充水，压力为大气压，流速为零。实验台如图17所示。

实验测得内衬PVC钢管时域信号为图18。

3.4. 结果分析

针对实验管材，分别进行了行波法和数值模拟计算，结果对比如表6。

由于管道内充有流体，使得管道的固有频率相比无水管道有所降低，行波法计算结果、数值模拟结果与实验结果相比误差均不大。

4. 双层复合管固有频率影响因素的讨论

采用行波法分别讨论尺寸，材料参数的变化对管道固有频率的影响规律。

4.1. 尺寸变化

算例1：选取三种双层管，分别为不锈钢-碳钢、黄铜-碳钢、陶瓷-碳钢管，黄铜密度8700 kg/m³，弹性模量92 GPa，陶瓷密度3500 kg/m³，弹性模量0.03 GPa，选定内层管厚度为3 mm，外层管厚度为7 mm，长度为3 m，两端简支，管道充水，流速为20 m/s，压强为1 MPa。管道内径分别为5，10，15，20，25，30 cm时，计算对应的管道固有频率，讨论不同管径对管道固有频率的影响。

由表7绘制成图19，无论是内外层材料性能相近，还是材料性能差别较大的双层管，其固有频率均随着管道内径的增大而增大。在管道半径较小的情况下，管道材料性能相近，管道固有频率相差较小，管道半径增大，管道材料性能对管道固有频率的影响增大。

算例2：管道长度l = 3 m，两端简支，管道充水，流速为20 m/s，压强为1 MPa。内层材料选择黄铜，外层材料选择碳钢，参数同1.4.管道内径为15 cm，管道总厚度为15 mm并保持不变。讨论当内层材料厚度分别为0，1，5，7.5 mm时管道固有频率的变化规律。

根据表8绘制成图20，可以看出对于双层管来说，在内层材料厚度较薄的时候，管道固有频率与单层管接近。在内层材料与外层材料厚度相当的情况下，双层复合管的固有频率与单层管相比，有明显的差异，随着固有频率阶数的增大，固有频率值相差增大。

算例3：选取黄铜-碳钢管，内径为15 cm，取内层管道厚度为3 mm，管道内外层厚度之比分别选1:1，1:3，1:5，1:8，1:10，分析内层厚度不变，外层厚度的变化对管道固有频率的影响。

由图21可以看出，在管道内径一定的条件下，随着管道外内层厚度比的增大，管道的固有频率增大。

4.2. 材料参数变化

算例4：管长3 m，内径为10 cm，两端简支，内层材料厚度3 mm，外层材料为碳钢，厚度7 mm，设定管道内层材料密度为7930 kg/m³，管道弹性模量分别取100，130，160，190，220，250 GPa。管道充水，流速为20 m/s，压强为1 MPa，分析管道内层材料弹性模量的变化对管道固有频率的影响见图22。

在管道其它条件不变的情况下，随着内层材料弹性模量的增大，管道的固有频率增大。

算例5：选取双层管，内径5 cm，内层材料厚度2 mm，外层材料厚度8 mm，外层材料为碳钢，管道长3 m，两端简支，管内液体选择水，流速20 m/s，压强1 MPa。内层材料弹性模量取100 GPa，密度取1000，2000，3000，4000，5000，6000，7000，8000，9000 kg/m³。计算管道固有频率。

由图23可以看出，管道材料密度增大，管道固有频率降低，对内径大的管道，固有频率变化更加明显。

Figure 17. Test bed for PVC steel lined steel pipe

图17. 内衬PVC钢管充水实验台

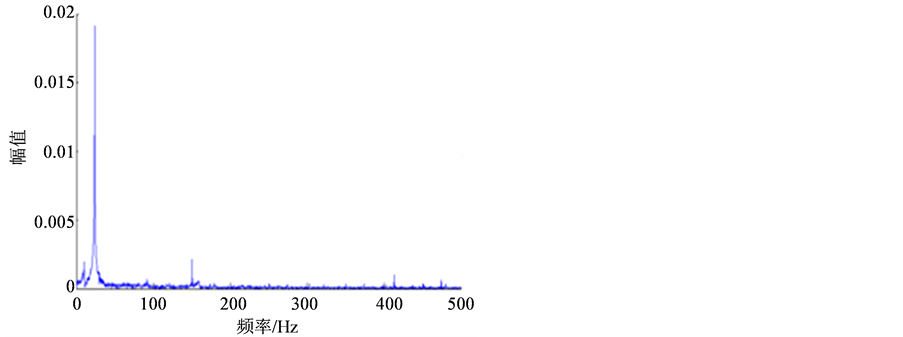
Figure 18. Time domain signal diagram for PVC lined steel pipe

图18. 内衬PVC钢管时域信号图

Table 6. Natural frequency of PVC lined steel pipe

表6. 内衬PVC钢管固有频率

Table 7. The first order natural frequency of pipe with different inner diameter

表7. 不同内径管道的一阶固有频率

Table 8. Natural frequency of brass-carbon steel pipes with different inner layer thickness

表8. 不同厚度黄铜碳钢管道的固有频率

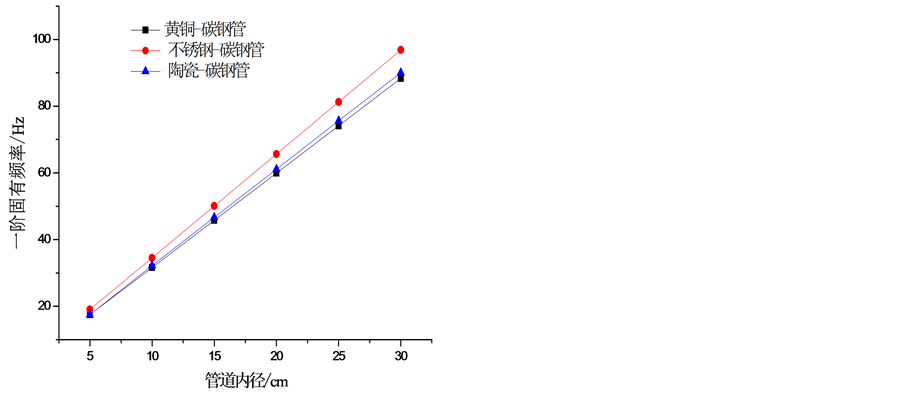
Figure 19. The first order natural frequency of pipe with different inner diameter

图19. 不同内径管道的一阶固有频率

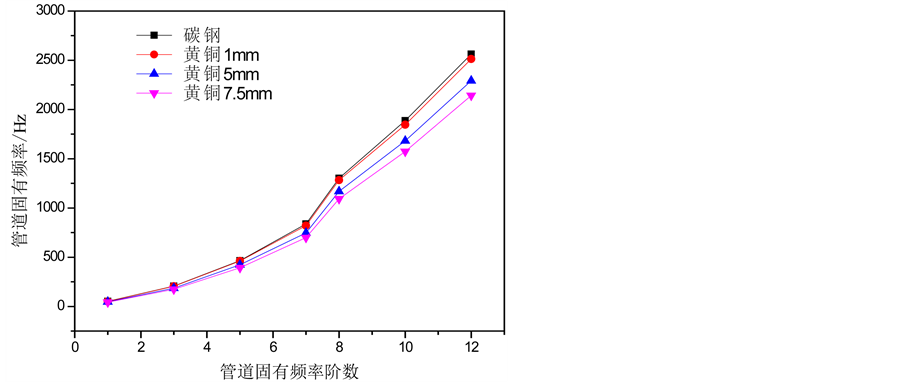
Figure 20. Natural frequency of brass-carbon steel pipes with different inner layer thickness

图20. 不同内层厚度黄铜碳钢管固有频率

Figure 21. The first order natural frequency of the pipe with different thickness of inner and outer layer

图21. 不同内外层厚度比管道的一阶固有频率

Figure 22. The first order natural frequency of the pipe with different elastic modulus

图22. 不同弹性模量下管道的一阶固有频率

Figure 23. Natural frequency of the pipe varies with the material density

图23. 管道固有频率随材料密度变化

5. 结论

双层复合管在工业中得到越来越广泛的应用。研究双层复合管的流固耦合振动对实际生产中设备的安全、经济运行具有重大意义。

1) 本文以工程中常用的双层复合管为研究对象，采用复合材料力学层合板的串、并联模型，对材料参数进行等效拟合，将双层管简化为单层管，通过对空管的理论计算、数值模拟和实验研究，得出并联模型的简化方法对金属材料管具有一定的准确性，串联模型简化方法对非金属的塑料管具有一定的准确性，为研究双层复合管流固耦合振动的动力特性提供了理论基础。

2) 对充液双层复合管流固耦合问题，运用行波法建立管道的流固耦合波导方程，代入等效参数进行求解，并与数值模拟结果和实验结果进行了比较得出结论：行波法解题思路清晰，宜于编程实现，且计算结果与已有成果吻合良好，表明该方法具有较高的数值精度，是解决工程复杂管路系统流固耦合问题的有效方法，具有较大的实用价值和广泛的应用前景。

基金项目

国家自然科学基金(11572237, 11372240)和中央高校基本科研业务费专项资金资助。