1. 包络的定义问题
微分方程通解曲线族的包络的定义 [1] 设给定单参数曲线族
 , (1)
, (1)
其中c是参数, 是x,y,c的连续可微函数。曲线族(1)的包络是指这样的曲线,它本身并不包含在曲线族(1)中,但过这曲线的每一点,都有曲线族(1)中的一条曲线和它在这点相切。
是x,y,c的连续可微函数。曲线族(1)的包络是指这样的曲线,它本身并不包含在曲线族(1)中,但过这曲线的每一点,都有曲线族(1)中的一条曲线和它在这点相切。
微分几何中曲线族的包络的定义 [2] 对于给定的平面曲线族Cλ: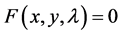 ,如果在这平面上存在曲线C,使得C与这族曲线中每一条曲线Cλ都相切,而且曲线C完全由这些切点组成,则平面曲线C称为这平面曲线族Cλ的包络。
,如果在这平面上存在曲线C,使得C与这族曲线中每一条曲线Cλ都相切,而且曲线C完全由这些切点组成,则平面曲线C称为这平面曲线族Cλ的包络。
从上面的两个定义可以看出,作为微分方程中曲线族的包络的曲线,要求的就是过它上面的每一点,都要有曲线族(1)中的一条曲线和它在这点相切。而作为微分几何中曲线族的包络的曲线,要求的是曲线族中的每一条曲线都要与它相切,同时,包络完全由这些切点组成。
我们说,作为微分方程中曲线族的包络,不能要求曲线族中的每一条曲线都要与它相切,否则,就无法建立微分方程(通解)曲线族的包络与奇解的等价关系,更无法利用求解通解曲线族的包络的方法确定微分方程的奇解了。因此,同为包络,由于在不同学科中的应用不完全相同,在具体的定义方面就产生了(也需要产生)一定的差异。
2. 举例说明
例1求微分方程
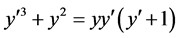 (2)
(2)
的奇解。
解方程(2)即为
 ,
,
 ,
,
 .
.
方程的通解为
 (3)
(3)
及
 , (4)
, (4)
还有一个特解为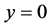 。
。
对积分曲线族(3)由于 ,所以(3)没有包络。对积分曲线族(4),
,所以(3)没有包络。对积分曲线族(4),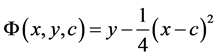 ,
,
 。c—判别式为
。c—判别式为

解得c—判别曲线为

由于 ,
,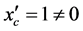 ,满足非蜕化条件,因此Γ是第二个积分曲线族(4)的包络,因而
,满足非蜕化条件,因此Γ是第二个积分曲线族(4)的包络,因而 是原方程的奇解。但是这里的
是原方程的奇解。但是这里的 不与积分曲线族(3) (其中
不与积分曲线族(3) (其中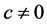 )中的曲线相切,也不相交。如果按照微分几何中包络的定义,
)中的曲线相切,也不相交。如果按照微分几何中包络的定义, 就不是方程通解曲线族的包络,也就得不到这个奇解了。
就不是方程通解曲线族的包络,也就得不到这个奇解了。
例2求微分方程
 (5)
(5)
的奇解。
解方程(5)即为
 ,
,
 .
.
方程的通解为
 (6)
(6)
及
 (7)
(7)
其中c1,c2为任意常数。不失一般性,可取 ,这样方程的通解可写为
,这样方程的通解可写为
 (8)
(8)
它的c—判别式为

解上面方程组,得到符合题意的一条c—判别曲线

对第一个积分曲线族
 ,
,
 ,
, .
.
满足非蜕化条件,因此Γ是第一个积分曲线族的包络, 是原方程的奇解。但是在积分曲线族(8)中,平行直线族
是原方程的奇解。但是在积分曲线族(8)中,平行直线族 与奇解
与奇解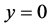 相交而不相切。如果按照微分几何中包络的定义,
相交而不相切。如果按照微分几何中包络的定义, 就不是曲线族(8)的包络,从而不能采用求包络的方法得到这个奇解了。
就不是曲线族(8)的包络,从而不能采用求包络的方法得到这个奇解了。
3. 求奇解时必须注意的一个问题
该问题通过举例加以说明。
例3判断方程
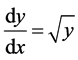 (9)
(9)
是否存在奇解,如果存在就求出来。
解右端函数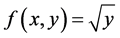 在
在 的上半平面定义、连续。
的上半平面定义、连续。

当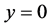 时无界,所以方程如果有奇解,只能是
时无界,所以方程如果有奇解,只能是 ,显然
,显然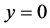 是方程的一个解,当
是方程的一个解,当 时可求得方程的通解为
时可求得方程的通解为
 ,
,
即
 , (10)
, (10)
其中 ,c是任意常数。现在求通解的包络,这里
,c是任意常数。现在求通解的包络,这里
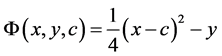 ,
,
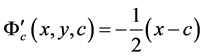 .
.
已知 是方程的解,而在通解中
是方程的解,而在通解中 时,
时, ,补充定义
,补充定义 。解方程组(c—判别式)
。解方程组(c—判别式)
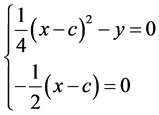
得c—判别曲线

由于 ,
, ,满足非蜕化条件,故c—判别曲线
,满足非蜕化条件,故c—判别曲线 为通解曲线族(10)的包络,从而为方程(9)的奇解。
为通解曲线族(10)的包络,从而为方程(9)的奇解。
注在求通解的过程中可知 !因此在c—判别式这个方程组中,x不能等于c!为此在解方程组求c—判别曲线之前必须补充定义函数值:
!因此在c—判别式这个方程组中,x不能等于c!为此在解方程组求c—判别曲线之前必须补充定义函数值: 时,
时,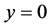 。否则
。否则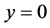 与积分曲线族(10) (其中,
与积分曲线族(10) (其中,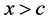 ,从而
,从而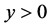 )没有公共点!谈何相切?
)没有公共点!谈何相切?
例4判断方程
 (11)
(11)
是否存在奇解,如果存在就求出来。
解右端函数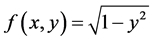 ,它在带形区域:
,它在带形区域: ,
, 上定义、连续。
上定义、连续。

当 时无界。所以方程如果有奇解,只能是
时无界。所以方程如果有奇解,只能是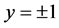 ,显然
,显然 是方程的两个解。当
是方程的两个解。当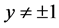 时可求得方程的通解为
时可求得方程的通解为
 ,
,
即
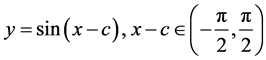 , (12)
, (12)
其中c是任意常数。现在求通解曲线族的包络,这里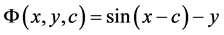 ,
,
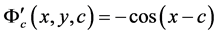 。已知
。已知 是方程的解,而在通解中当
是方程的解,而在通解中当 时
时 ,补充定义
,补充定义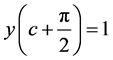 ;同理,补充定义
;同理,补充定义 ,解方程组(c—判别式)
,解方程组(c—判别式)

得两条c—判别曲线
 与
与
对这两条c—判别曲线,均有 ,
,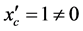 ,满足非蜕化条件。故两条c—判别曲线
,满足非蜕化条件。故两条c—判别曲线 与
与
 都是通解曲线族(12) (这时
都是通解曲线族(12) (这时 )的包络,从而是方程(11)的奇解。
)的包络,从而是方程(11)的奇解。
注与前面类似,通解是当 时得到的,这时
时得到的,这时 !同样,在解方程组求c—判别曲线之前必须补充定义函数值:当
!同样,在解方程组求c—判别曲线之前必须补充定义函数值:当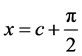 时
时 ;当
;当 时,
时, 。
。
当然,对于例3也可以这么解:当允许 (或
(或 )时,通解(10)就表示了方程所有的解,接下来可以直接解方程组求c—判别曲线,而不必定义函数值。同样,对于例4,也可以这样叙述:当允许
)时,通解(10)就表示了方程所有的解,接下来可以直接解方程组求c—判别曲线,而不必定义函数值。同样,对于例4,也可以这样叙述:当允许
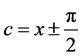 (或)时,通解(12),其中,就表示了方程所有的解,接下来可以直接
(或)时,通解(12),其中,就表示了方程所有的解,接下来可以直接
解方程组求c—判别曲线,而不必定义函数值。