Fe-X (X = Si, Cr, Mn, Ni)二元合金结构和弹性性质的第一性原理计算

First-Principles Study on Structure and Elastic Properties of Fe-X (X = Si, Cr, Mn, Ni) Binary Alloy

摘要: 采用基于密度泛函理论的第一性原理计算方法，系统研究了Si, Cr, Mn, Ni等合金元素对面心立方结构Fe的晶体结构和弹性性质的影响规律。结果表明，不同合金化元素(Si, Cr, Mn, Ni)的加入都使面心立方Fe晶胞的晶格常数增大，晶胞体积增加。加入合金元素后，二元合金体系都满足力学稳定性条件；弹性常数C₁₁, C₁₂和C₄₄几乎都增加，弹性模量都出现增大，泊松比整体变化不大。

Abstract: The effects of alloying element such as Si, Cr, Mn and Ni on the structure and elastic properties of face centered cubic Fe were investigated by the method of the first-principles based on density functional theory. The results showed that the alloying elements (Si, Cr, Mn, Ni) were all increased the lattice constant of face centered cubic Fe, and thus increased the cell volume. After adding the alloying elements, the all binary alloy systems meet the mechanical stability conditions. The elastic constants of C₁₁, C₁₂, and C₄₄ were increased almost all, the elastic moduli were increased also and the Poisson’s ratio was changed little as a whole.

1. 引言

钢铁材料是我们非常熟悉的基础材料，在日常生活和生产中具有举足轻重的作用，其具有优良的塑性、冲击韧性和电磁性能，在国防、能源、交通、电子以及航空航天等领域有着广泛的运用。工业中很少用到纯铁，通常以合金化的形式被应用在生活的方方面面，通过加入元素，使金属成为(在一定的工艺条件下)具有预期性能的合金。

钢的合金化是改善其组织和力学性能的主要方式之一，添加适量的合金化元素可提高钢铁材料的力学性能和工艺性能。常见的合金化元素有C, Cr, Si, Mn, Co, Ni, Ti, V, W, Nb等等，这些合金化元素主要以固溶强化、第二相强化以及细晶强化等方式发挥作用 [1] [2] 。其中，Si能提高钢铁的抗拉强度和屈服强度，特别能提高弹性极限 [2] 。Cr的主要作用是提高钢的淬透性和耐回火性，使钢具有高的接触疲劳强度和耐磨性，还可以增加钢的硬度和强度，Cr还是提高钢的抗腐蚀性的主要元素之一，几乎所有不锈钢中都含有Cr [3] 。Mn能细化钢的晶粒，提高钢的淬火深度，改善许多钢种的抗拉强度、可加工性、韧性、硬度和耐磨性，含锰高强度低合金钢已成主要钢种之一 [2] [4] 。Ni会促使奥氏体相的形成从而提高合金钢的力学性能，并在提高钢强度的同时，改善塑性、淬透性、可焊接性等，同时提高其耐蚀性 [5] 。

第一性原理计算只用电子质量、光速、质子中子质量等少数实验数据进行量子计算而不依赖任何经验参数即可合理预测微观体系的状态和性质。它只需要知道构成微观体系各元素的原子序数，就可以应用量子力学计算出该微观体系的物理性质。随着计算机能力的提高和第一性原理的不断完善，其在材料科学基础研究中的应用也越来越广泛 [6] 。因此，本文采用第一性原理计算的方法，对添加不同合金元素Si, Cr, Mn, Ni后面心立方结构Fe的晶体结构和弹性性质等展开系统研究，并得到相关规律，以期为高性能合金钢的获得提供一定的理论支持和指导。

2. 计算方法和模型

本文的计算结果是采用Materials Studio软件中的CASTEP(Cambridge serial total energy package)模块，根据密度泛函理论利用平面波超软(Ultrasoft)赝势法进行计算得到的。计算中采用基于广义梯度近似(GGA)的PW91交换关联法对Kohn-Sham方程和能量泛函进行自洽求解。

面心立方Fe的空间群为FM-3M，计算过程中采用的价电子组态为：Fe3d4s, Si3s3p, Cr3d4s, Mn3d4s, Ni3d4s。几何优化时采用的平面波的截断能为300 eV，在自洽计算(SCF)时应用Pulay密度混合法，结构优化的收敛条件为每个原子的能量变化在1.0 × 10⁻⁶ eV以内；原子最大受力不超过0.03 eV/Å；最大压力不超过0.05 GPa；最大位移不超过0.001 Å。采用Monkhorst-Pack方法划分K点网格，k取7 × 7 × 7，考虑自旋极化进行计算。

为了使计算的结果更加准确，在计算中采用2 × 2 × 2的超晶胞作为完整晶体的计算单元，总原子数为32个，用Fe₃₂表示。计算发现一个合金元素原子置换Fe超胞顶角位置的Fe原子时，系统的总能量较低，因此采用合金元素原子置换Fe₃₂顶角的一个Fe原子后的晶胞作为计算单元，得到的二元合金的计算单元分别用Fe₃₁Si, Fe₃₁Cr, Fe₃₁Mn和Fe₃₁Ni表示。

不同晶系中独立的弹性常数个数不同，立方晶系中有三个独立的弹性常数，分别为：C₁₁, C₁₂和C₄₄。根据计算出的独立弹性常数，通过Voigt-Reuss-Hill近似 [7] ，进一步得到体模量B和剪切模量G。

Voigt模型中，体模量Bv和剪切模量Gv与弹性常数的关系为：

$B_V=\frac{1}{3}\left(C_{11}+2C_{12}\right)$ (1)

$G_V=\frac{1}{15}\left(C_{11}-C_{12}+3C_{44}\right)$ (2)

在Reuss模型中，体模量BR和剪切模量GR与弹性模量的关系可表述为：

$B_R=\frac{1}{3S_{11}+6S_{12}}$ (3)

$G_R=15{\left[4\left(S_{11}-S_{12}\right)+3S_{44}\right]}^{-1}$ (4)

其中， $C_{44}=S_{44}$ ， $C_{11}-C_{12}={\left(S_{11}-S_{12}\right)}^{-1}$ ， $C_{11}+2C_{12}={\left(S_{11}+2S_{12}\right)}^{-1}$ 。这里的 $S_{ij}$ 是柔性常数，因此可以得到：

$B_V=B_R=\frac{1}{3}\left(C_{11}+2C_{12}\right)$ (5)

$G_R=\frac{15\left(C_{11}-C_{12}\right)C_{44}}{4C_{44}+3\left(C_{11}-C_{12}\right)}$ (6)

Hill模型的体模量B和剪切模量G可以通过将Voigt和Reuss模型的计算结果进行平均值简化得到，即：

$B=\frac{1}{2}\left(B_V+B_R\right)$ (7)

$G=\frac{1}{2}\left(G_V+G_R\right)$ (8)

杨氏模量E和泊松比v可通过体模量B和剪切模量G得到：

$E=\frac{9BG}{3B+G}$ (9)

$v=\frac{3B-2G}{2\left(3B+G\right)}$ (10)

3. 结果与讨论

3.1. 晶体结构

图1是计算过程中使用的Fe₃₂(a)和Fe₃₁Si(b)超晶胞的晶胞结构图。Fe₃₁Cr, Fe₃₁Mn和Fe₃₁Ni的晶胞结构图与Fe₃₁Si类似，仅合金化元素不同，此处不重复给出。在计算过程中，我们先对单晶胞面心立方Fe进行了结构优化，优化后的晶格常数a = 3.447Å，与已知实验值a = 3.56 Å [8] 的误差为3.17%，在误差允许范围之内，说明了计算的准确性。

之后采用超晶胞计算了加入不同合金化元素后面心立方结构Fe的晶格参数，结果如表1所示。从表1中的数据可以看出，不同合金化元素(Si, Cr, Mn, Ni)的加入都会导致面心立方Fe晶胞晶格常数的增大，从而引起晶胞体积的增加，其中Ni元素导致的增加程度最大，而Cr元素的增加程度最小。

3.2. 弹性性质

本文计算得到的面心立方Fe(Fe₃₂)以及加入不同合金元素(Si, Cr, Mn, Ni)后的面心立方Fe(Fe₃₁Si, Fe₃₁Cr, Fe₃₁Mn和Fe₃₁Ni)的弹性常数如表2所示。

立方晶系的力学性能稳定性条件为 $\left(C_{11}-C_{12}\right)>0$ ， $C_{11}>0$ ， $C_{44}>0$ ， $\left(C_{11}+2C_{12}\right)>0$ [9] ，若满足此条件，则说明各合金体系满足力学稳定性条件，可以稳定存在。由表2可知，到Fe₃₂和Fe₃₁Si, Fe₃₁Cr, Fe₃₁Mn, Fe₃₁Ni均满足力学稳定性条件，不同合金化元素(Si, Cr, Mn, Ni)的加入没有破坏面心立方Fe的稳定状态。

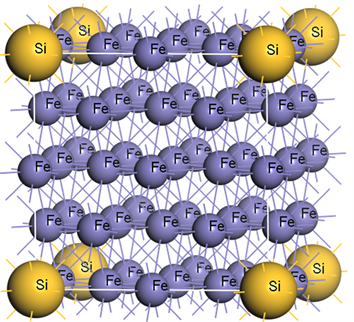(a) (b)

Figure 1. The unit cell structure of Fe₃₂(a) and Fe₃₁Si(b)

图1. Fe₃₂(a)和Fe₃₁Si(b)的晶胞结构图

Table 1. The lattice parameter of Fe and Fe-X(X = Si, Cr, Mn, Ni) binary alloy

表1. Fe和Fe-X(X = Si, Cr, Mn, Ni)二元合金的晶格参数

由表2也可以看出，与Fe₃₂相比，Fe₃₁Si, Fe₃₁Cr, Fe₃₁Mn和Fe₃₁Ni的弹性常数C₁₁和C₄₄都出现增大，只有Fe₃₁Ni的C₁₂出现降低。这说明合金元素Si, Cr, Mn的加入使面心立方Fe在[100]、[111]和[011]方向的抗变形能力都得到增加。Ni元素的加入使面心立方Fe在[100]和[011]方向的抗变形能力增大，而在[111]方向的抗变形能力有所减弱。

从表2中还可以看出，Fe₃₁Ni的C₁₁增加最多，说明Ni元素的加入使面心立方Fe在[100]方向的抗变形能力增大的程度最大，而Fe₃₁Cr的C₁₂和C₄₄增加最多，说明Cr元素的加入则使面心立方Fe在[111]和[011]方向的抗变形能力增加程度最大。

表3是计算得到的Fe₃₂和Fe₃₁X₁(X = Si, Cr, Mn, Ni)的体模量(B)、弹性模量(G)、杨氏模量(E)以及泊松比(v)。体模量B可以表征材料抵抗断裂的能力，剪切模量G可以表征材料抵抗塑性形变的能力，杨氏模量E表征材料抵抗弹性变形的能力。此外，虽然不同晶系材料的硬度与其弹性模量的关系不尽相同，但是一般来说杨氏模量和剪切模量的数值越大，材料的硬度越高 [10] 。由表3中的数据可以看出，合金元素加入后，面心立方Fe的体模量、剪切模量和杨氏模量都出现了增加，说明合金元素(Si, Cr, Mn, Ni)的加入都使面心立方Fe的抗断裂能力、抗塑性变形和弹性变形的能力得到提高，同时硬度增加。由表中也可以看出，Fe₃₁Ni的杨氏模量和剪切模量数值相对最大，而Fe₃₁Cr的则相对较小，说明Ni元素的加入使面心立方Fe的硬度增加的幅度相对较大，而Cr元素的增加幅度相对较小。此外，由表中可以看出，加入不同合金元素后，计算得到的二元合金的体模量数值都大于剪切模量，说明影响这些合金机械性能稳定性的限制条件为剪切模量 [11] 。

泊松比是描述材料横向变形的弹性常数，反映材料的侧向收缩能力，泊松比越小，物质中的共价键越强，其相应的硬度就越高，反之，泊松比越大，塑性越好，硬度就越低 [12] 。由表3中可以看出，总体来说，本研究中合金元素的加入对泊松比的影响不大，其中Si元素的加入对面心立方Fe的泊松比数值无影响，Cr元素使其略有增加，而Mn和Ni元素使其泊松比减小，其中Fe₃₁Ni的泊松比数值最小。结

Table 2. The calculated elastic constants of Fe and Fe-X(X = Si, Cr, M, Ni) binary alloy

表2. Fe和Fe-X(X = Si, Cr, Mn, Ni)二元合金的弹性常数

Table 3. Calculated bulk, shear and Young’s modulus and Poisson coefficient for Fe and Fe-X(X = Si, Cr, Mn, Ni) binary alloy

表3. Fe和Fe-X(X = Si, Cr, Mn, Ni)二元合金的弹性模量和泊松比

合之前有关弹性模量的分析，可以发现，Ni元素的加入使面心立方Fe的硬度增加较为显著，而Cr元素使其增加的程度相对较小。

4. 结论

通过采用第一性原理计算的方法研究了Fe-X(X = Si, Cr, Mn, Ni)二元合金的晶体结构和弹性性质。得到的主要结论包括：1) 晶体结构的研究结果表明，不同合金化元素(Si, Cr, Mn, Ni)的加入都使面心立方Fe晶胞的晶格常数增大，晶胞体积增加，其中Ni元素导致的增加程度最大。2) 弹性性质的研究表明，各二元合金体系满足力学稳定性条件。Si, Cr, Mn和Ni的加入基本都使弹性常数C11, C12和C44增加，仅Ni元素的C12出现下降。Fe₃₁Ni的C11增加幅度最大，而Fe₃₁Cr的C11和C44增加幅度最大，说明Ni元素的加入使面心立方Fe在[100]方向的抗变形能力增大的程度最大，而Cr元素的加入则使面心立方Fe在[111]和[011]方向的抗变形能力增加程度最大。3) Fe-X(X = Si, Cr, Mn, Ni)二元合金的体模量、剪切模量和杨氏模量都出现了增加，说明合金元素的加入都使面心立方Fe的抗断裂能力、抗塑性变形和弹性变形的能力得到提高，同时硬度增加，其中Ni元素使硬度增加的程度较大，而Cr元素的增加程度相对较小。影响Fe-X(X = Si, Cr, Mn, Ni)二元合金机械性能稳定性的限制条件为剪切模量。