1. 引言
随着分布式电源(distributed generation, DG)技术和配电网技术的快速发展,目前配电网的高级发展阶段——主动配电网,其最为显著的特征就是大量的分布式电源的接入。如何在新的发展形势下高效利用分布式电源,因此迫切需要加强对分布式电源的接入对主动配电网的影响的研究。分布式电源的接入使配电系统从放射状无源网络变为了接有分散电源的有源网络,可能出现功率双向流动,将会对保护配置、电压调整、电能质量、运行管理等产生直接而深刻的影响。同时,分布式电源对丰富能源供应方式、提高能源利用效率、保障可持续发展有着重要意义,应积极稳步加以应用。
目前对于分布式电源的接入对配电网稳态电压的影响分析主要有两个方面的研究,一是通过建立电压和分布式电源接入容量、接入位置的关系数学模型,以节点电压不越限为目标,得到分布式电源最大接入功率 [1] [2] [3] [4] ;二是以分布式电源最大接入功率为目标,将节点电压、线路功率等作为约束条件,得到分布式电源的优化规划 [5] [6] [7] [8] 。其中计算分布式电源准入容量的方法主要有试探法、解析法和数学优化法 [9] ,其中解析法比较繁琐,但是解析描述的方法比潮流数值分析更能揭示问题本质。数学优化发的系统建模复杂,如果建立有效的数学模型要考虑各种约束,而且计算量大。
为了研究主动配电网中分布式电源接入对稳态电压分布的影响,本文采用解析方法作为分析手段,采用开式网络电压损耗的近似计算方法进行解析推导。通过对分布式电源接入后稳态电压的分布特点和节点电压要求,分析在不造成电压越限情况下分布式电源的最大可接入容量,同时还分析了线路调压器对于分布式电源接入后电压分布的影响。
2. 稳态电压分布
2.1. 分布式电源和负荷模型
我国配电网主要以放射状链式结构为主,在主动配电网发展初期,也以该具有诸多优点的网络结构作为主要的运行网络结构,在主动配电网控制及管理技术发展过程中,可能会出现网格型闭环网络等形式。研究分布式电源接入对主动配电网的电压影响时,可将配电网上游大网络等值为一定内阻抗的电压源,中低压配电线路充电电容、线路互感、漏电阻可以忽略。考虑到配电网常采用就地无功补偿,线路中流动的无功很小,故在有关推导中将垂直分量忽略。
本文负荷采用恒功率模型,分布式电源也视为恒功率拟负荷特性稳态模型。文献 [10] 基于恒电流负荷模型和恒电流分布式电源稳态模型对配网电压进行了分析,随着越来越多的分布式电源参与电压调节,将分布式电源作为恒电流源的等值方式不再适用。正常情况下,恒功率静态负荷吸收的有功、无功不随电压变化而变动。分布式电源视为拟负荷特性的恒功率模型,可以保证分布式电源向配电网注入有功功率、无功功率不随接入点电压变化而变动。馈线稳态电压一般从首端直尾端呈逐渐下降的趋势。分布式电源并网后输出一定的有功和无功功率,使得配电系统中传输的有功、无功潮流发生变化,于是线路上电压的分布也发生相应的变化。
2.2. 考虑离散负荷时的稳态电压分布
1) 两节点简单接线
对一个两节点的配电网,其单线等值电路如图1所示,忽略了三相配电线路之间的互感。令送端母线为参考节点的线电压
,线路每一相的阻抗为
,线路末端的DG作为另一个节点,其线电压为
。
先不考虑分布式电源和机端负荷,且认为参考节点的电压始终不变,若将垂直分量
忽略,末端节点电压的数值为
(1)
其中
为负荷节点的电压损耗。
若不计DG注入功率引起的线路损耗,则线路中潮流的变化等于DG注入功率
,则节点1在DG并入前后的电压变化
(2)
可见,分布式电源并网后,若DG不从配网吸收系统无功,负荷节点的电压上升。DG因减少馈线中传输的功率并提供一定无功支持,对负荷节点的电压支撑是有利的。
2) 多节点链式网络
沿馈线将每一集中负荷视为一个负荷节点并加以编号。变电所母线编号为0,负荷节点一次为
。每一小段线路的电阻和电抗分别为
、
,形成的配电网络如图2所示。
根据两节点电压损耗的推导结果,可将上图中所示的多节点链式网络的每一段
均视为两节点系统,则第n节点的电压损耗
可以视为前面所有小段的损耗之和。
(3)
经过一些简化,例如忽略线路阻抗的功率损耗、将分母中的电压均看做是
,最后推导出在接入DG前后,馈线上各节点的电压幅值变化量
为:
(4)
若馈线上接有M台DG,分别接入在
节点上。M台DG将馈线分为
段,相应各段区间内个节点的电压损耗可以分别计算得到。
相应节点上的电压可以通过系统电压减去电压损耗得到:
(5)
在上述计算公式中并没有考虑线路阻抗上的功率损耗,因此计算出的电压损耗会比真实值略偏小。
2.3. 考虑连续负荷时电压分布的解析分析
可以采用解析法求得负荷为连续分布情况下配电线路的电压分布 [10] 。根据统计,分析中可假设负荷满足平均分布、高斯分布或随机分布等分布规律。例如平均分布,如果馈线长度为
;令单位长度线路的阻抗为
;馈线上负荷平均分布,各处负荷的电流大小可以表示成对应距离的函数,如图3所示,并以
表示。线路上任一处的电压为
。线路上
处,接有一个注入电流
的DG。
若在
处有一台DG接入,则该位置前后两个区间内各点相对于送端的电压损耗为:
(6)
电压损耗主要由相应位置处的过剩电流(流向下游的总电流与DG注入电流之差)决定。如果线路上有多台DG注入,电压损耗的表达式也比较容易获得,只需对
区间根据DG接入点位置进行分段积分。
若馈线中有M台DG,分别接在
处接入电网。将系统节点视为
,则馈线的电压损耗的表达式为:

Figure 3. Feeder model with continuous distributed load
图3. 负荷近似连续分布的馈线模型
式中
。
进一步将接入配电系统中多个DG的注入的电流也视为随位置变化的函数
,则可以认为电压分布表达得更一般化,电压损耗与过剩电流直接有关,如下式所示:
(8)
2.4. 线路调压器的影响
分布式电源接入配电网,使得馈线电压被抬高;电压升高的同时动态负荷的无功需求量会有所减少,电容补偿的无功也增多,这样系统中因DG接入的净无功变化会多于DG的无功出力。同样,一个部分依靠接入DG支撑电压的配电线路,DG的退出,使得电压下跌;动态负荷无功需求增加,电容发出的无功减少,这样配电线路缺额的无功会远远大于退出的DG所发出的无功。
线路调压器是常用的电压调整设备。其可以在额定电压20%的范围内对输入电压进行自动调节。在线路中端或者末端安装调压器可以使整个线路的电压质量得到保证;对负荷较重的线路,线路压降大,在线路中端加装调压器也可以改善整条线路的电压质量;调压器也可安装在变电站主变压器出线侧,实现有载调压。
2.5. 分布式电源最大可接入容量的研究
基于2.3节给出的DG接入后配电网节点电压分布的解析描述,下面将研究影响DG最大可接入容量的影响因素。从对电压影响的角度,建立DG可行接入位置、最大可接入容量限制的基本依据。
2.5.1. 分布式电源可行接入位置
在潮流分析中,功率分点是一个关键位置信息。因配电网中无功流动较少,配电网中的功率分点一般指有功分点,而且可以通过解析方法推得。由式(6) (8)得到电压的解析表达式,对电压求距离的导数得电压随距离变化的灵敏度:
(9)
电压灵敏度为零的位置对应为功率分点。假设在距离
处,电压灵敏度为零,则有:
(10)
如果网络保持严格吸型受端网络的性质,则上式方程必然有解,所得解
为功率分点。该点是DG接入配电网很重要的参考位置。从物理意义上理解,电压灵敏度为零的位置对应潮流方向发生变化的位置,通常对应局部极小电压的位置。
考察DG接入点处的电压灵敏度,若在接入位置电压正负逼近方向的灵敏度的绝对值相等,DG接入点的电压将更为稳定一些。为此,有:
(11)
即有:
(12)
解上式可得到DG的临界可行接入位置
。在临界可行接入位置以后的位置接入DG,则会使全局电压极小出现在公路分点而非馈线末端,常常会给运行人员造成误解。
2.5.2. 分布式电源最大接入容量
DG的接入位置确定以后,注入功率是需要考虑的另一个关键问题。考察
之间电压的上升区,如果方程
有解
,则说明在
处电压与送端电压相同。保证该方程有解的必要条件是
,且解
必然满足不等式
。
因电压在区间
单调上升,所以局部极大电压只能出现在
。若假设配电网中馈线各处的电压不得高于变电所母线电压,
处按压损耗
,即
小于
对应下式:
(13)
如果定义DG临界注入容量为
,则其计算式为:
(14)
电压上下限约束对应的DG最大注入容量,可以通过下面的不等式求出:
(15)
其中
是送端电压,
是馈线正常运行的上限电压。
上述推导均是基于单台DG接入的情形,可以很容易推广到多台DG接入的网络。多台DG接入的情形,馈线被划分为更多的区间,功率分点是一组解,而且解得存在性也更为复杂。临界注入容量在各区间均有各自的解。
3. 仿真算例
3.1. 算例条件
采用20节点的单馈线系统作为仿真算例。每个节点负荷不尽相等,线路的长度也不相等。DG的数量可变,接入位置可选择非系统母线节点以外的任意节点。系统母线电压取为1.02 pu。所有负荷与DG的出力均是相对于10 MVA的标幺值,电压基值为10 kV。算例中考虑1台至3台DG接入到系统中,各分布式电源的出力和接入的节点号如表1所示。
3.2. 算例分析
馈线上的负荷累计0.8 pu,属于馈线负荷率的正常水平。表1中3台DG都接入系统时DG的渗透率(渗透率定义为DG注入系统有功功率之和与对应网络有功峰荷的比值)为40.21%。算例做了如下仿真:① 1台DG分别接入7、13、19节点和同时接入对节点电压的影响;② 3台DG接入节点7、13、19;接入节点2、4、6;全部接入10节点;全部接入末节点20节点;③ 3台DG接入节点7、13、19其注入功率发生变化,即渗透率发生变化;④ DG与线路调压器的配合;⑤ 可行接入位置和可接入容量分析。
仿真结果表明DG接入不同位置对节点电压的影响不同。DG接入点越接近线路末端,对线路电压的支撑作用越明显。如果分散接入于馈线中,将比单独接入时对线路电压的支撑作用更好。
从图4可以看出,总出力相同的DG,分布在不同的位置组合,得到的电压分布也有较大的差异。渗透率到一定程度后,可能会使线路末端的电压抬得太高,使线路末端电压不再是馈线的最低电压。这和DG具体接入位置有关系。以上结论和用其他潮流分析方法得到的结论一致。
整个仿真中采用静态恒功率负荷,实际配电系统中有一定的动态负荷和无功电压调节设备。这些负荷或设备的无功需求随电压的变化而动态变化。DG的接入和退出并不简单就是DG出力的数字变化,实际情况会更复杂。
表1. 各分布式电源的出力和接入的节点号

Figure 4. Voltage profile curves with different DG locations
图4. 三台DG接入不同位置
在本算例中仅考虑DG接入前后电压稳态变化与线路调压器分接头调整的关系。仿真中线路调压器考虑负荷的一侧安装可调绕组,即选用直接式的线路调压器。本算例中将线路调压器安装在线路中间位置即节点10上。DG的出力情况如3.1节中所述。
从图5可以看出,当不接入DG时,馈线末端节点电压接近下限水平,当DG接入但是无线路调压器的配合时,线路末端节点电压也较低,无法使末端电压达到期望的额定电压水平。DG未接入时采用线
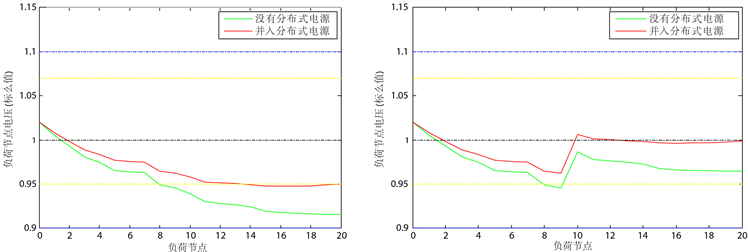
Figure 5. Voltage profile curves of DG with line regulator
图5. DG与线路调压器配合
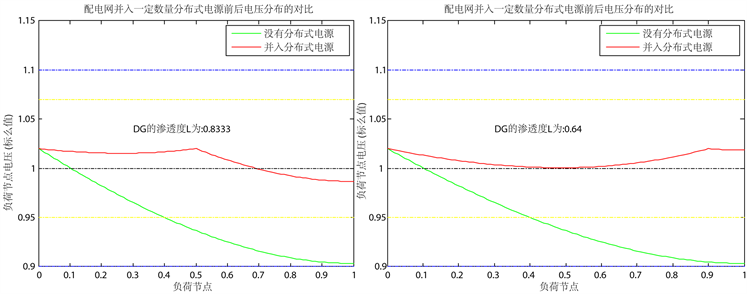
Figure 6. Voltage profile curves of max penetration of DG with different locations
图6. DG在不同位置注入临界容量的电压分布图

Table 2. Max penetration of DG with different locations under voltage limit
表2. 电压不越限情况下DG接入位置和对应的最大注入容量
路调压器可以明显抬高末端节点电压,此时如果再接入DG,DG与线路调压器配合使用,可以使线路末端节点电压达到额定电压水平。
假设馈线的总阻抗为0.2 pu,并满足平均分布。首端电流
等于0.5 pu,增长速度为1 pu/单位长度,则馈线负荷的分布为:
(16)
假定网络额定运行。如果假定此时接入的DG渗透率
为30%,可解出功率分点位于线路的黄金分割点0.618,临界可行接入位置为0.8229。
图6显示了DG在线路0.5 pu处和0.9 pu注入临界容量的电压分布情况。DG接入位置在0.5 pu时,该位置在功率分点之前,电压由两段持续下降的曲线组成,前一段下降的速度要小于后半段。DG接入位置在0.9 pu时,线路末端的电压会高于功率分点处的电压,使得全局电压极小点出现在线路中间。临界注入容量明显呈持续降低的趋势,这说明考虑到电压调节问题,越距离线路末端的位置所能接纳的DG注入越小,越接近系统母线所能接纳的DG注入越大。
如果只保证馈线上的电压不越限的情况下,计算分布式电源接入的最大接入容量,DG接在不同位置的最大可接入容量如表2所示。
从表2可以看出,仅考虑电压不越限的约束条件,无论分布式电源接入在线路的任何位置,分布式电源的最大可接入容量均超过馈线最大负荷,都会因为分布式电源的接入产生逆流,馈线上的潮流反向。主动配电网将通过主动控制与主动管理技术、灵活的网架结构等来处理该问题,既满足电压不越限,又可以不致迷惑电网运行人员。
4. 结论
本文首先利用稳态恒功率的负荷模型及分布式电源模型,推导离散型负荷的稳态电压分布,进而推广到一般性连续解析形式的稳态电压分布。离散型负荷分析得到的分布式电源接入对于稳态电压分布的影响与其他分析方法得到的结论一致。
通过对稳态电压分布的特点和要求,分析了在不造成电压越限情况下分布式电源的最大可接入容量,仿真结果表明,如果只考虑馈线节点电压不越限的约束条件,分布式电源的最大可接入容量均超过最大负荷,引起馈线潮流倒送。同时还分析了线路调压器对于分布式电源接入后电压分布的影响。因此,只有合理选择容量、接入位置并与调压器紧密配合,分布式电源可作为一种可实用的电力支撑和调压手段。以上结论可为在主动配电网规划时考虑全局无功优化以及一二次协调规划提供理论基础。