1. 引言
诺贝尔奖得主费曼于1959年美国物理学会年会上提出了纳米科技的概念,揭开人类进军纳米科技的序幕。分子机器属于纳米科技范畴,它由分子构件组成,具有小尺寸、多样性、自适应,以及仅依靠热能、光照或者化学能驱动等其他人造机器难以比拟的优点,因而在许多领域中具有广阔的应用前景。由于在分子机器研究方面作出了杰出贡献 [1] - [6] ,索维奇、斯图达特和费林加共同获得2016年的诺贝尔奖。
分子机器常用热能进行驱动,期间将伴随着热传导。只有通过高效的热传导,才能使热量到达指定位置及部件而进行高效的热驱动。也只有通过高效的热传导,才能避免分子机器工作期间因聚集过多的热量,而使部件乃至整个分子机器因过热而失效。因此研究分子机器构件的热传导性质,显得十分重要的。由于尺寸过于微小,目前对分子机器构件的热传导性质进行实验研究还存在较大困难,只能在理论研究方面进行探索,然而遗憾的是,迄今为止也没有他人开展过这方面工作。由于晶格动力学考虑了晶格振动的量子效应,能得到比较准确的结果,并且基于该理论能推导得到热传导系数的解析公式,便于分析热传导性质的物理机制,因此我们曾用晶格动力学研究过分子机器中环状分子这种常用构件的热传导性质 [7] ,并得到了一些有意义的结果。作为分子机器中另一种最常用构件的链状分子,其结构与环状分子有很大的差异,由于在其两端处声波发生反射,致使它的热传导性质与环状分子肯定不会相同,因此有必要对链状分子的热传导性质单独进行理论研究。在本文中我们将用晶格动力学研究分子机器中链状分子的热传导性质,分析其物理机制,并将链状分子与环状分子的热传导性质进行比较。
2. 链状分子的晶格动力学与热传导理论
分子机器中链状分子构件的热学性质取决于其原子振动。在文献 [8] 中我们已经根据晶格动力学理论,得到和谐近似下链状分子中原子l的振动位移、动量公式和频率公式。设n个原子质量为m的相同原子构成链状分子,a为原子间距离,β为原子间线性力常数,和谐近似下链状分子中原子l的振动位移和动量可表示为:
(1)
(2)
其中,
为普朗克常数,
代表
,
代表
,
和
为声子产生与消灭算符,链状分子振动频率
可由下式计算:
(3)
由(1)式和(2)式可知,链状分子以驻波形式振动,波矢大小
为
,其中,
。
对应于链状分子整体平动,此处不作考虑。
链状分子中原子的波动会引起能量传播,能量通量可由下式计算 [9] :
(4)
将(1)式和(2)式代入(4)式,通过计算得到链状分子振动的能量通量公式:
(5)
其中,
,且
取奇数。
(6)
其中,
为波矢
对应的群速度,可由下式计算:
(7)
将能量通量代入Green-Kubo公式 [9] ,即可计算系统的热传导系数λ。将时间积分区间扩展至
,Green-Kubo公式可表示为:
(8)
其中,T为温度,
为玻尔兹曼常数,
为平均值。
将(5)式代入(8)式,并根据时间关联函数的解耦公式 [10] :
(9)
得:
(10)
根据文献 [10] ,上式中的声子产生算符与消灭算符之间的时间关联函数可由以下公式计算:
(11)
(12)
其中,
为声子谱线宽度,
是平均声子数,其符合玻色统计:
(13)
将(11)式和(12)式代入(10)式,并进行积分,得链状分子热传导系数计算公式:
(14)
上式中,
取奇数。只对
求和,即得声子j对热传导系数的贡献
。由上面公式可知,链状和环状分子的能量通量及热传导系数公式完全不同 [7] ,因此有必要对其热传导性质单独展开研究。由(14)式可知,如果想通过该式计算链状分子的热传导系数,我们还必须计算各个声子的谱线宽度
。
3. 链状分子的声子格林函数与声子谱线宽度
实际链状分子中原子间存在三阶非和谐相互作用势能,这将导致声子间发生相互碰撞,而使声子具有有限的寿命。实际链状分子振动哈密顿可表示为和谐项和三次非和谐项之和,根据计算得:
(15)
其中,
(16)
上式中,γ为三阶非和谐力常数。
为奇数时
取非零值。
定义时域声子Green函数 [7] [10] :
(17)
采用与文献(7)相同的方法,得频域声子Green函数:
(18)
其中,
(19)
将
中ω取值
,并分解为实部
和虚部
之和。由于格林函数的极点实部代表声子频谱,而极点虚部代表声子谱线宽度,故得以下声子谱线宽度公式:
(20)
在上式中,设置各个声子谱线宽度的迭代初值,经过有限次迭代收敛后,即可得各个声子的谱线宽度。
当
取值为
时,(20)式转化为:
(21)
上式与Maradudine等人得到的大块晶体声子谱线宽度公式形式上是一致的 [11] ,这也说明推导(20)式的过程是正确的。在使用(21)式进行数值计算时,由于狄拉克
不好直接处理,Maradudine等人在使用(21)式时,用
替代
进行数值计算 [11] ,其中η的合理选择对于计算结果非常重要:如果η选择太小,则没有足够的声子模式之间进行碰撞,如果η选择过大,则让一些本来无法碰撞的声子能够进行碰撞,从而都得出不正确的结果。对于该参数的选取,Turney等人 [12] 和鲍华 [13] 从经验出发,建议选择
,据此得以下声子谱线宽度公式:
(22)
比较(22)式和(20)式可知,根据Turney等人从经验出发给出的η系数
得到的声子谱线宽度公式与我们给出的声子谱线宽度公式不同,在我们的公式中,相当于η系数取了
。由于我们给出的公式是经过严格推导得到的,故而更为准确。由此可见,我们的声子谱线计算结果要比由Maradudine等人和Turney等人的方法得到的声子谱线计算结果更为准确。
4. 数值计算结果与分析
虽然氩原子构成的链状构件在分子机器中没有具体应用,但由于氩原子间的相互作用能用L-J模型准确描述 [14] ,因此在本文中通过对它进行计算来了解链状分子的热膨胀性质的尺寸效应。要计算热传导系数,首先得计算声子谱线宽度。设温度60 K,并设各个声子谱线宽度的初值,运用(20)式,经过有限次迭代快速收敛后,即可得各个声子的谱线宽度。计算得到的不同长度的链状分子的声子谱线宽度
与波矢
关系曲线如图1所示,其中
等于
。由图可知,当链状分子较短时,随链状分子的长度增加,
关系曲线上移;当链状分子较长时,如N达到40时,再增加链状分子的长度,
关系曲线基本保持不变。将声子谱线宽度代入(14)式进行数值计算,即可得链状分子的热传导系数。
在温度为60 K时,根据(14)式及声子谱线宽度数据计算得到的不同长度的链状分子的热传导系数λ如图2所示。为了便于比较,图中还出示了相同条件下的环状分子的热传导系数结果 [7] 。由图2可知,链状分子热传导系数随其长度变化规律类似于环状分子,即其热传导系数随其长度增加而增加。由于两端处存在声波的反射,相同长度的链状分子和环状分子的热传导系数相比要小很多,当两者长度增加时热传导与长度的关系曲线并不趋于重合,反而差距越大。
为了揭示长度趋于无穷时,在温度为60 K下热传导系数λ随长度n的变化规律,在图3中给出了
的关系曲线,当N趋于无穷时该曲线趋于的渐进值ρ为
。由此可见,当链状分子长度n趋于无穷时,其热传导系数λ按
的规律趋于无穷,即热传导系数不会收敛。类似于当长度趋于无穷时链状分子的热传导系数趋于无穷的现象,在其它的一些一维系统中也存在 [15] [16] 。
为了分析原子链的热传导的物理机制,我们还计算了不同长度的原子链的中各种波矢
的声子对热传导的贡献
,如图4所示。由图4知,当链状分子中原子个数增加时,
的关系曲线变窄,重心向短波矢方向移动,说明长链状分子中短波矢的声子对热传导系数贡献变大,而长波矢声子对热传导系数贡献变小,从而长链状分子的热传导系数主要来自于短波矢声子贡献。

Figure 1. Phonon linewidth vs. wave vector
图1. 声子谱线宽度与波矢之间的关系

Figure 2. Heat conductivity of chain molecule vs. its length
图2. 热传导系数与链状分子长度的关系

Figure 3. Heat conductivity of chain molecule vs. its length (ordinate:
)
图3. 热传导系数与链状分子长度的关系(纵坐标:
)
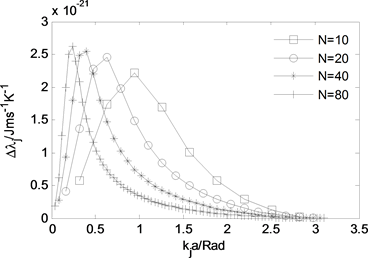
Figure 4. The contribution made by phonon to heat conductivity vs. wave vector
图4. 声子对热传导系数贡献与波矢之间关系
5. 结论
本文运用晶格动力学理论和格林–久保公式,推导出链状分子的热传导系数公式,在此基础上进行了数值计算,最终根据数值计算结果总结链状分子的热传导系数随其长度变化的规律。研究结果表明,链状分子热传导系数随其长度的变化规律类似于环状分子,即其热传导系数随其长度增加而增加,当长度趋于无穷时,热传导系数也趋于无穷。但相同长度的链状分子和环状分子的热传导系数相比要小很多,当两者长度趋于无限时热传导与长度的关系曲线并不趋于重合,反而差距越大。长链状分子热传导系数主要来自于短波矢声子的贡献。