1. 引言
在常规能源逐渐枯竭、环境污染日益严重的情况下,世界各国积极开发、利用可再生能源,并将光伏发电视为重要发展领域。随着光伏发电技术的快速发展和大规模的商业化应用,现有的电力系统不断向高效、清洁、灵活的方向发展,整个社会的能源利用效率有所提高。然而,分布式光伏接入后配电网由无源网络变为有源网络,可能出现电压越限、继电保护装置误动或拒动等问题,需要对此进行定量分析,并得出分布式光伏的最大接入容量。
目前,分布式光伏接入对配电网电能质量影响的研究主要集中在电压偏差与电压波动方面。文献 [1] [2] [3] [4] [5] 针对大量分布式光伏电源接入配电网后的电压偏差等问题展开分析,建立了计算分布式电源准入容量的数学模型;文献 [6] [7] 针对分布式光伏接入配电网后产生的谐波污染问题展开了研究,并得出谐波污染限制下配电网的光伏准入功率;文献 [8] 针对电压偏差和谐波约束,提出了配网光伏最大渗透率评估方法。然而分布式光伏准入功率不仅需要考虑其对于电能质量的影响,还要分析其对于电流保护的影响。文献 [9] 分析了光伏并网发电对保护及重合闸的影响,并提出了相应的应对措施。目前,尚无综合考虑配电网电能质量与电流保护的光伏准入容量研究。
本文针对配电网对分布式光伏的接纳能力,首先采用恒功率分布式光伏与负荷模型,推导了分布式光伏接入对配电网电压偏差的影响,分析了分布式光伏对配电网电压谐波的影响;其次分析了分布式光伏接入后对故障电流的影响情况。利用某区域实际配电网算例,计算并得出在电能质量约束以及不改变现有电流保护整定值的条件下,分布式光伏的最大接入容量。
2. 分布式光伏接入对配电网电能质量的影响
2.1. 分布式光伏接入后对配电网的电压偏差的影响
考虑如图1所示的配电网络,沿配电网馈线
将每一个集中负荷视为一个节点进行编号,有
个节点,第
个节点的电压是
,线路始端电压是
,线路标准电压是
,
为节点i相对线路始端节点的电压降落;每个节点间的线路阻抗相同,设相邻节点之间的线路阻抗大小设为
;配电网系统的负荷均匀分布在线路馈线点端,负荷功率大小设为
,接在节点i处的分布式光伏系统容量以
表示。
不考虑分布式光伏接入时,配电网在节点i处的电压偏差
表达式如下所示:
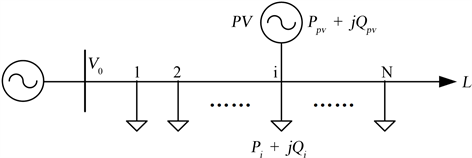
Figure 1. Multi node constant power distribution network
图1. 多节点恒功率配电网络
(1)
当单独考虑分布式光伏系统作用于配电网时,先将配电网的系统电源侧短路,配电网线路中的阻抗相对于负荷而言比较小,故分布式光伏系统对电压偏差的作用主要表现在分布式光伏系统到系统电源这一段,也就是i点之前的线路;而对于i点之后的线路,分布式光伏系统对电压偏差没有直接的影响,但由于分布式光伏系统的接入,可能对电压有抬高的作用,从而会间接的影响i点后的各点电压偏差,故在此规定分布式光伏系统对电压降的作用为负。故,在分布式光伏系统单独作用下,节点j的电压降落
为:
(2)
利用电路叠加定理:
,得到配电网中任意一点j处同时在系统电源和分布式光伏系统作用下的电压降:
(3)
由前面可知,此配电网的线路端电压是
,则线路中任意一点j的电压是:
(4)
则,含分布式光伏系统的配电网在节点j处的电压偏差
表达式如下所示:
(5)
由方程式(5)可知,分布式光伏系统的接入容量、接入位置均会影响到配电网节点的电压偏差。
2.2. 新能源系统接入对谐波电压畸变量的影响
在距变压器低压侧G km处接入非线性模型的分布式光伏系统。谐波分析时分布式光伏系统采用谐波电流源来模拟,其
次谐波电流幅值为
,以基于分布式光伏系统流出的基波电流
的百分比表示:
次谐波电流相角为
。接入分布式光伏系统的简化谐波网络图,如图2所示。
2.2.1. 分布式光伏系统接入容量对谐波电压畸变量的影响
分布式光伏系统流出的基波电流幅值是:
(6)
推导后得出,接入分布式光伏系统后末端节点的谐波电压幅值变化量
为:
(7)
式中,
为第h次谐波注入电流幅值,
与
分别为分布式光伏接入前与接入后的h次谐波电压幅值,
为h次谐波注入电流幅值,G是变压器低压侧到分布式光伏系统的距离;L是变压器低压侧到负荷的距离。
当分布式光伏系统采用电压控制的运行模式,则
基本保持不变;当
增大时,由方程式(6)可知,
变大。
越大,
越大,即谐波电压畸变水平升高得越高。
2.2.2. 分布式光伏系统接入位置对谐波电压畸变量的影响
假设分布式光伏系统分别接入配电网线路的
和
处,且有
。比较两种接入情况下,即考虑线路
处于两种不同位置(
和
)时,谐波电压畸变水平的变化差异。
1) 分布式光伏系统接入线路
之前
(
)位置的谐波电压幅值可表示为:
。由于分布式光伏系统采用电压控制的运行模式,则
基本保持不变,
不变时,由方程式(2)可知,在分布式光伏系统的接入节点分别为
和
时,
几乎相同。而
越大,线路末端节点电压
就越高,在分布式光伏系统的接入节点为
时的
比接入节点为
时的
小。因此,随着接入位置
的增大,分布式光伏系统接入点
之前
(
)位置的谐波电压幅值
减小,谐波电压畸变水平降低。
2) 分布式光伏系统接入线路
之后
(
)位置的谐波电压幅值可表示为:当分布式光伏系统接入位置为
时,
;当分布式光伏系统接入位置为
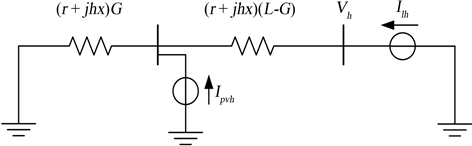
Figure 2. Distribution network for harmonic analysis
图2. 用于谐波分析的配电网络
时,
。两式相减得,
,即
;因此,随着接入位置
的增大,分布式光伏系统接入点
之后
处的谐波电压
变大,谐波电压畸变水平升高。
3. 分布式光伏接入对配电网电流保护的影响
分布式光伏对配电网电流保护的主要影响是向短路点提供故障电流。当不改变分布式光伏接入位置与容量时,短路点位置也会影响分布式光伏提供的短路电流,因此需要考虑在线路不同位置发生短路故障时,分布式光伏能够提供的故障电流量;此外,当线路相同位置发生短路故障的情况下,随着分布式光伏接入位置和接入容量的改变,配电网中分布式光伏提供的短路电流同样有着较大的改变。分布式光伏的容量增加,所能提供的故障电流增加;因此本节主要研究配电网中短路点位置与分布式光伏接入位置的相对关系对故障注入电流的影响。
以图3所示的配电网络为例进行继电保护分析。图3中f1点发生短路时,只有系统电源经保护R1向故障点提供短路电流,同时分布式光伏通过保护R2向故障点提供短路电流。对于三相短路的情况可等效为如图4的简单电路,分布式光伏用一个受控电流源来表示,节点3右侧的负荷用ZL表示,
为节点1与节点2之间的线路阻抗,
为短路处距线路始端线路的阻抗,与
。
此时流过保护R1的短路电流是:
(8)
根据图4,利用节点电压法可以得到分布式光伏端电压
的表达式:
(9)
由于分布式光伏采用最大功率输出模式,且常以单位功率因数运行,因此这里假定
;另外假定图4中线路型号均相同,即认为所有线路的阻抗角均相同。设,
,线路阻抗角均为
。
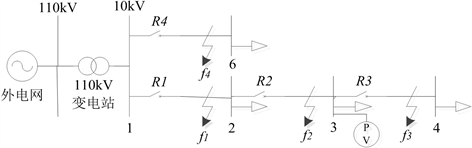
Figure 3. Distribution network for relaying protection analysis
图3. 用于继电保护分析的配电网络
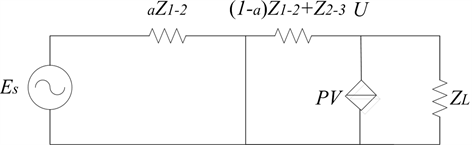
Figure 4. Equivalent circuit diagram for short circuit at f1
图4. f1点发生短路时的等效电路图
故由方程式(9)并进一步展开可以得到:
(10)
由此即可解出分布式光伏端电压
的大小以及流过保护R2的短路电流:
(11)
(12)
通过上面分析可知,保护R1能够准确的切除其保护范围内的故障,但是,保护R2有可能检测到故障电流而先动作,从而使分布式光伏右侧形成孤岛运行状态。
当f2、f3与f4点发生短路时,分析的方法与f1点发生短路时一致,具体推导过程在此不再赘述。
4. 算例分析
采用图5所示的某地区的实际配电网进行仿真分析,此配电网共包含2条支路,6个节点,每个节点末端都带有一定功率的负荷,其中分布式光伏系统主要通过支路节点末端接入配电网。
系统侧电压等级选取110 kV,系统阻抗值
,
;110 kV主变的容量选择是63 MVA,变压器变比是110/10.5,容载比取2.56,功率因数取0.95,110 kV母线电压标幺值取1.0,110 kV母线电压基准值取110 kV,10 kV线路电压基准值取10.5 kV;10 kV公用配变的容量选择是0.8 MVA,变压器变比是10/0.4。线路参数为:电阻是0.125 W/km,电抗是0.08 W/km,电纳是2S × 10−6/km,每段线路长度为1 km。
各节点的负荷情况如下:节点2、节点3和节点4处的负荷值均为2.23 MW,节点5负荷取10 kV公用配变的极限容量0.8 MW,节点6用于模拟110 kV变电站其余10 kV线路的负荷,负荷值为12.02 MW。
4.1. 考虑电能质量的分布式光伏准入容量
4.1.1. 电压偏差
选取线路极限容量的5%、25%、50%、75%和100% (0.669 WM、3.345 MW、6.69 MW、10.035 MW和13.38 MW)五种情况作为分布式光伏的接入容量,在光伏接入容量发生变化时各节点电压偏差如表1所示。
从表1中可以看出,当线路潮流方向不发生变化时,随着分布式光伏接入容量的增加,减小了配电网节点电压偏差;但是当分布式光伏接入容量超过6.69 MW时,线路潮流方向发生变化,配电网节点电压偏差由负转正,随着分布式光伏系统接入容量的继续增加,配电网节点电压偏差开始增加,在选择的光伏接入容量下,未出现节点电压偏差越限的情况。
选取节点2、节点3和节点4作为分布式光伏的接入位置,分布式光伏接入容量设定为13.38 MW。
通过表2可知,随着分布式光伏接入位置越靠近线路末端,配电网节点电压偏差越大,当分布式光伏接入节点4且接入容量取13.38 MW时,配电网节点4的电压偏差超出了GB/T 12325-2008《电能质量 供电电压允许偏差》规定的±7%的范围,此时接入节点4的分布式光伏的最大接入容量是10.41 MW。
4.1.2. 电压谐波
采用同样的方式针对电压谐波总畸变率展开研究,光伏接入容量变化时各节点电压谐波总畸变率如表3所示。由表3可知,配电网节点电压谐波总畸变率与光伏接入容量正相关,随着光伏接入容量的增

Figure 5. A typical distribution network
图5. 典型配电网络

Table 1. Node voltage deviation when the PV capacity changes
表1. 光伏接入容量变化时节点电压偏差

Table 2. Node voltage deviation when the PV location changes
表2. 光伏接入位置变化时各节点电压偏差

Table 3. Node voltage deviation when the PV capacity changes
表3. 光伏接入容量变化时各节点电压谐波总畸变率
加,配电网节点电压谐波总畸变率也相应增加,当分布式光伏接入容量取13.38 MW时,配电网节点2、节点3和节点4的电压谐波总畸变率均超出了GB/T 14549-2008《电能质量公用电网谐波》规定的±4%的范围,此时对应的接入节点3的分布式光伏最大接入容量是11.78 MW。
当分布式光伏接入位置变化时,各节点电压谐波总畸变率情况如表4所示。
通过表4可知,分布式光伏接入点的电压谐波总畸变率与分布式光伏接入位置无关,仅与分布式光伏的接入容量有关;且分布式光伏接入位置越靠近线路末端,分布式光伏谐波传播的距离越远,谐波衰减的程度越大,配电网其余节点的电压谐波总畸变率越小。当分布式光伏分别接入节点2、节点3和节点4且接入容量取13.38 MW时,配电网节点2、节点3和节点4的电压谐波总畸变率均超出了GB/T 14549-2008《电能质量公用电网谐波》规定的±4%的范围,此时接入节点2、节点3和节点4的分布式光伏的最大接入容量是11.78 MW。
通过对比表3和表4可知,含分布式光伏的配电网节点电压偏差越限时对应的分布式光伏的最大接入容量,小于含分布式光伏的配电网节点电压谐波总畸变率越限时对应的分布式光伏的最大接入容量。因此,当含分布式光伏光伏的配电网节点电压偏差和节点电压谐波总畸变率同时越限时,应该优先考虑节点电压偏差越限问题。
4.2. 考虑电流保护的分布式光伏准入容量
本文以分布式光伏接入前配电网的电流保护整定值为约束,分析该条件下分布式光伏接入的最大容量。其中三段式电流保护R1、R2、R3和R4电流速断保护的整定应按躲开下级线路保护母线侧短路时可能出现的最大短路电流来整定。I段可靠性系数取为1.2,II段可靠系数取为1.1,III段可靠系数取为1.15、自启动系数取为1.3、电流继电器的返回系数取为0.85。假设线路末端保护配置电流速断保护和过电流保护,其余线路保护配置电流速断、限时电流速断和过电流保护三段保护。不考虑分布式光伏接入的情况下,对保护1~4的整定计算结果如表5所示。
表6为结合表5和表6可知,当短路点取f3且分布式光伏接入容量取10.35 MW时,流过保护R2的故障电流(15.244 kA)小于其限时电流速断整定值(15.27 kA),使得保护R2的二段保护无法作为R3的远后备保护,此时对应的接入节点3的分布式光伏最大接入容量是10.01 MW。
结合表5和表7可知,当短路点取f3且分布式光伏接入容量取13.38 MW时,流过保护R2的故障电流(17.703 kA)小于其限时电流速断整定值(17.151 kA),使得保护R2与保护R3同时动作切除故障而失去选择性,此时对应的接入节点2的分布式光伏最大接入容量是12.96 MW。

Table 4. Node voltage deviation when the PV location changes
表4. 光伏接入位置变化时各节点电压谐波总畸变率

Table 5. Feeder current protection setting value without considering distributed PV
表5. 不考虑分布式光伏接入的馈线电流保护整定值(kA)

Table 6. Short circuit current effective value of each protection when the PV capacity changes
表6. 光伏接入容量变化时各保护流过的短路电流有效值(kA)

Table 7. Short circuit current effective value of each protection when the PV location changes
表7. 光伏接入位置变化时各保护流过的短路电流有效值
表8. 光伏准入容量
4.3. 综合考虑电能质量与电流保护的分布式光伏准入容量
在分别得出考虑电能质量与电流保护的分布式光伏准入容量之后,进行汇总并得出综合考虑以上多种因素的分布式光伏准入容量。根据表8可知,综合考虑电压偏差、电压谐波以及电流保护三类约束的条件下,本文算例中节点2、节点3与节点4的光伏准入容量分别为12.65 MW、10.01 MW以及10.41 MW。
5. 结论
本文针对分布式光伏接入后,配电网电能质量与故障电流的变化情况展开分析,通过实际算例分别得到考虑电压偏差、电压谐波以及电流保护的光伏准入容量,并得到综合考虑以上因素的光伏准入容量。本文的分析结论不仅可判断配电网中某一节点的光伏准入容量,还可得出该准入容量的相应限制条件,为配电网的调整与改造提供参考。
基金项目
国家电网公司科技项目:新能源运行特点及接入系统适应性研究(SGTYHT/15-JS-191)。