1. 引言
随着机械工业、航空工业、以及国防工业的不断发展,对小尺寸孔径或轴类零件提出精密或超精密的加工要求的同时,也对其检测精度提出了更高的要求,而对于目前已经现有的孔径测量技术都或多或少存在一些问题,例如接触式测量仪其中的坐标测量机测量法、电接触法,坐标测量机测量法测孔径其测头端容易磨损并且对于受测孔径内径的材质也有一定的限制 [1] [2] ,电接触法测孔径受到被测孔端面情况、线规端部情况、孔的清洁程度以及线规本身的尺寸精度、圆度、直线度等诸因素的影响,使得这种方法的测量精度不高。而且更重要的是,这是一种综合测量,不可能测得小孔的任意截面的尺寸和形状误差 [3] 。非接触式测量仪其中的气动式孔径测量仪,只能综合地反映小孔对气体流过的影响,属于孔截面的测量 [4] ,而不能测得任意截面的尺寸和形状误差,故应用范围受到局限 [5] [6] [7] 。因此研究更加方便的微孔内径精密测量方法具有重要的研究意义。
本文在光学显微共焦点技术的基础上,结合几何光学系统成像原理 [8] ,设计出一种能高精度测量微小圆孔内径以及内径分布的测量系统。分析了测量原理,并给出了实验案例。这种方法可以极大地克服测量微孔内径时受到活动空间的限制、操作调整不便等缺点。还具有非接触式测量,避免了测头对被测件的损害。
2. 光学显微共聚焦测量技术原理
2.1. 原理光路
光学显微共聚焦测量技术原理光路如图1所示。物方显微物镜将光纤光源发出的光会聚于系统主光轴上的一点。当该点与相机焦平面相对于成像系统为一对物像共轭位置时,在相机前设置针孔滤波后,相机上将观察到清晰的、呈圆形形状的焦点的图像 [9] 。这个图像称为焦斑。将待测工件沿光轴的垂直方向靠近焦点位置时,若对于该焦点形成一定的遮挡,焦斑形状会发生变形,呈部分圆形形状。当待测工件刚好和光学系统的光轴重合时,焦斑形状呈规则半圆形状。所以可以根据焦斑形状,确定工件与光轴之间的相对位置。
2.2. 实验装置
完整的测量内孔直径的原理测量图如下图2所示,包括光源、光纤、照明显微物镜、反射镜、精密电动平移台、成像物镜以及CCD相机。移动精密平移载物台 [10] ,由于聚焦点与被测工件之间的相对位置发生变化,从而在相机焦平面将观察到共焦点的图像形状(焦斑形状)的变化 [9] 。
3. 测量原理
在图2所示测量光学系统结构中,首先调整物方显微物镜与成像系统共轴、共聚焦。在实际测量圆孔内径时,左右前后调整工作台的位置,使得测量系统的聚焦位置位于待测圆孔内部。再通过左右控制精密电动平移台,使聚焦点位置位于待测圆孔直径相对的两个端点孔壁上,分别记录聚焦点位于内壁左右两端时两个半圆(焦斑)直径对应的X坐标。具体过程图解如下。
1) 当系统内的聚焦点不在圆孔内壁上时,在相机上观察到的图像焦点的完整的像,仍然为一个完整

Figure 1. Principle diagram of confocal focus measurement
图1. 共焦点聚焦测量原理图
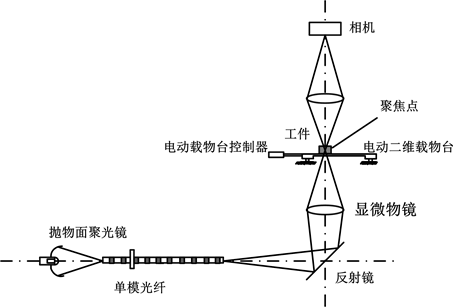
Figure 2. Optical structure diagram of aperture measurement system
图2. 孔径测量系统结构光路图
的圆,如下图3(b)所示;2) 系统内的聚焦点处于圆孔内壁上任意位置时,在相机上观察到的图像为半个焦点的像,即为半圆形;3) 如果聚焦位置处于圆孔内X或者Y方向直径所对应的圆孔的内壁上时,相机获得的半圆形状将处于系统的Y坐标轴或者X坐标轴划分的半个视场中。因此当聚焦点分别处于直径相对的两个端点孔壁上时,形成的两个半圆完全对称相反。如图3(a)、图3(c)表示聚焦点位置位于X轴方向直径的两个端点时的情况。这样可以根据图3(a)、图3(c)时半圆焦斑对应的X的坐标位置之差,测得圆孔的内径。
为了确定聚焦点位置位于X方向或者Y方向直径的两个端点,本实验系统采用了图像识别和图像匹配的方法。首先在图像中根据光学系统的参数设置,确定理论上的两个相反的半圆焦斑的形状、位置与大小,设置两个相应的焦斑半圆形状模板;然后在每幅图像中通过设置阈值的方法将图像二值化,确定图像中采集的焦斑图像的形状与位置,将焦斑图像形状与两个理论模板分别进行匹配,从而可以确定直径的两个端点位置。
因此,在精密电动平移台的控制 [10] 之下,通过图像识别和匹配,寻找具有两个相对的半圆形焦斑的所在坐标位置,再通过计算两坐标之差,即可测得圆孔的内径的大小。由此可见,整个系统的测量精度和误差主要取决于精密电动平移台的步长精度与误差,而通过改变聚焦位置在圆孔内部的深度,还可以测量圆孔内径沿深度方向的分布信息。
4. 实验案例
为了验证上述测量原理,在数字显微镜上实际测量了一个标称直径的30 cm的圆孔状样品。显微成像光学系统的倍率为10倍,手动调整载物台的位置,得到的一组对称形状的焦斑图像如图4所示,测得两次位置之差为29.9 cm,测量值和标称值基本一致,其误差为0.3%。图5为增加系统的放大倍数为40倍以后,拍摄到的图像为待测样品的局部。因为采用高倍显微成像系统,所以可以得到更精确的前后两次位置信息,从而提高系统的测量精度。而对于孔径较小的微孔,也可以通过增加系统的光学倍率,来实现高精度的测量。
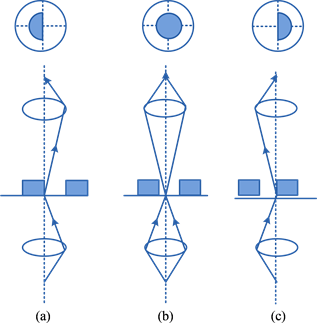
Figure 3. Schematic diagram of change of focal spot shape
图3. 焦斑形状变化示意图

Figure 4. A group of symmetrical focal spots (the system magnification is 10)
图4. 系统放大倍率为10倍时的一组对称的焦斑图像

Figure 5. A group of symmetrical focal spots (the system magnification is 40)
图5. 系统放大倍率为40倍时的一组对称的焦斑图像
5. 总结
本文研究了一种以共焦点三维形貌测量技术为基础,结合几何光学图像的形成原理,精确地测量圆孔内径的方法。分析了测量原理阐述了实验步骤过程,并进行了简单的实验验证。在实际的应用中,可以通过步进电机结合图像识别的方法,提高测量的精度。在微孔的测量中,也可以通过增加系统的光学放大倍率来实现高精度测量。与传统的圆孔内径测量方法相比,本文所研究的圆孔内径测量方法由于利用光学共焦点显微技术测量,测量的活动空间不受限制,操作调整方便,因此能够很大程度上解决各个领域对于圆孔内径精密测量的需求问题。
基金项目
江苏省淮阴师范学院大学生创新训练计划项目(201717001XJ),淮安市科技计划项目(HAGZ201601)。
参考文献
[1] 杨世民. 盲小孔与狭槽三维测头的研究[D]. 天津: 天津大学精密仪器与光电子工程学院, 1993.
[2] 肖贵福. 对发展坐标测量机测头的新思考[J]. 现代测量与实验室管理, 1995(4): 4-9.
[3] 王东浩, 等. 微型控制的电接触微孔测量方法[J]. 计量技术, 1991(1): 8-9.
[4] 叶宗茂. 气动测量技术[J]. 汽车工艺师, 2005(10): 34-37.
[5] Liaw, C.-J. and Brown, F.T. (1990) Nonlinear Dynamics of an Electrohydraulic Flapper Nozzle Valva. Journal of Dynamic Systems, Measurement and Control, Transactions ASME, 112, 298-304. https://doi.org/10.1115/1.2896139
[6] Bell, T.A. (1999) Industrial Needs in Solids Flow for the 21st Century. Powder Handling and Processing, 11, 9-12.
[7] Suzuki, K and Ukita, A. (1995) Improving Characteristics of Electrohydraulic Servo System by using DSP. Transactions of the Japan Society of Mechanical Engineers C, 61, 606-611. https://doi.org/10.1299/kikaic.61.606
[8] 姜春玲. 几何光学光路及成像过程模拟实现的研究[D]. 山东科技大学, 2004.
[9] 景敏. 数字图像处理技术的应用[J]. 机械管理开发, 2011(1): 201-202.
[10] 刘泽, 贾伟, 张晓飞, 等. 精密电动平移台驱动系统的设计[J]. 现代科学仪器, 2010(6): 17-20.