1. 引言
人们每天都在使用直流电器,例如手机,笔记本电脑等。
典型的直流电路具有一个电池,电池二端由金属导线连接一个负载电阻。金属导线内自由电子的运动速度是很慢的,小于1毫米/秒。可是电路中电能的传播速度非常快,传输速度是真空光速的数量级。例如,在电路的开关闭合时,电路中的电灯几乎是在一瞬间同时发光。由此可见,电路中的电能速度主要是由电场传输速度决定,而不是导体内的自由电子的运动速度。
关于直流电能传输相关的物理过程,许多大学电磁学教课书认为电能是在导线外部通过坡印亭矢量传输到电路内部的,见下面的图1。这个图示取自一本有名的大学电磁学教科书 [1] 。
在图1中,箭头代表电磁能流,即坡印亭能流矢量。图示表明:电池向外界空间输出电磁能量,然后电阻从外界空间吸收电磁能量。图示右上角的图中的Sn代表坡印亭能流矢量。坡印亭是19世纪的一
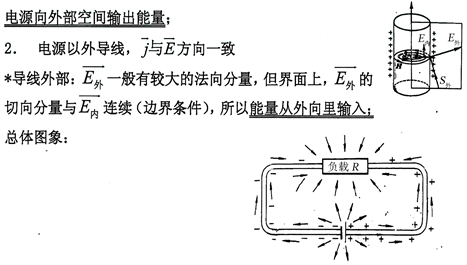
Figure 1. Schematic diagram of electromagnetic energy flow in a DC circuit
图1. 直流电路中电磁能流的示意图
d 位英国科学家(J.P. Poynting),他从Maxwell方程组推导出了坡印亭定理 [2] [3] 。这个定理类似于经典力学中的能量守恒定理,在数学上类似于连续性方程。
在直流电路以及低频交流电路的情况,本文指出:导线内的电能的传输过程与位移电流无关,所以也与坡印亭定理无关。
2. 坡印亭定理的推导
可以用三维微分算子的运算法则推导坡印亭定理。一个简单推导如下 [4] [5] [6] [7] :
根据推广的安培定律,
,(1)
其中jc是传导电流密度,方程式(1)的右边第2项是位移电流。使用E点积方程式(1)的两边,
(2)
再使用矢量算符的操作,我们得到
(3)
把(3)代入(2),我们容易得到
(4)
按照法拉第定律:
,我们得到
(5)
对于介电常数和磁导率e,和磁导率m,
(6)
把(6)代入(5),可以得到
(7)
定义
,是坡印亭矢量(电磁能流),其中
是坡印亭矢量的散度;
是电场对带电物体起作用的功率(jc是电流密度,E是电场,•是点积)。方程式(7)右边第二项是电能和磁能密度。因此,波印亭定理是经典电动力学中电磁能量守恒的表述。
当把E的点积代入方程(1)的两边进行运算时,我们必须考虑我们采取微分运算的局部微小点在哪里。如果这个局部微小点在导线之外,则传导电流密度jc为零,并且在自由空间中也是
。在直流电路以及低频交流电路的情况,导线内的电能的传输过程与位移电流无关,因此可以对上述坡印亭定理的推导提出质疑。
3. 对坡印廷定理的再思考
我们这里讨论的直流电是指不随时间变化的稳恒电流。在这种情况下,公式(1)中右边第2项的位移电流为0。于是公式(1)成为安培定律的经典形式:
(8)
公式(8)的微分形式来源于安培定律的积分形式:通电导线的周围有环形磁场。而电流以及传导电流密度jc是由电池的电动势驱动导线中的大量电子产生的。使用E点积方程(8)的两边,
(9)
从物理意义上说,方程(9)的右边代表导线内部的电功率密度,方程(9)左边物理意义是不明确的。它究竟是代表导线内部的物理量还是导线外部的物理量?如果它是代表导线外部的物理量,jc = 0,方程(9)左边也是0。如果它是代表导线内部的物理量,那么方程(9)左边的H不能代表通电导线周围的环形磁场。
由方程(9),我们注意到:在直流电路的情况下,上一节推导出的坡印亭矢量只是一个数学定义。它在直流电路没有形成真正的能流。图1显示的大学电磁学教课书的观点:“认为电能是在导线外部通过坡印亭矢量传输到电路内部的观点”,是不正确的。
库仑静电场是纵向电场。在直流电路中,金属线中的电场也是纵向电场。虽然这两个电场有一些相似之处,但事实上电源是有差别的。库仑静电场的电源是孤立电荷,直流电路的电源是电池,电池通过金属线连接到负载电阻器。
在直流电路的情况下,通电导线边界处的电场的边界条件并不清楚的,是否存在净电荷也是不明确的。由于静电场可以用金属盖屏蔽,所以我们对于直流电路做了一些测试。在直流电路中,我们串联一个电流表。1) 我们用金属盖屏蔽电池;2) 我们用金属盖屏蔽电阻器;3) 我们使用同轴电缆屏蔽内部电线。结果如下:电流表的读数基本相同(精度为4位)。这些测试表明,在直流电路中,外部电场(包括金属线界面附近的外部电场)的分布对金属线内的电场基本上没有影响。
总之,直流电能的传输过程与位移电流无关,所以也与坡印亭定理无关。在直流电路的情况下,电路内部的大量自由电子在电源的电动势的驱动下运动,电动势能转化为自由电子动能,形成了电流。在这种情况下,坡印亭矢量只是一个数学定义,它没有形成真正的能流,所以电磁能流不是从金属导线的外部传输到内部的。也就是说,直流电能完全是在通电导线的内部传输的。
在推导坡印亭定理的过程中,从方程(4)到方程(5),用到了法拉第定律。这个过程说明必须有个交变磁场产生交变电场的物理过程。这个过程在自由空间以及绝缘介质中的电磁波存在。
另外,当用上述经典的微分算子把E的点积代入方程(1)的两边进行运算时,我们必须考虑我们采取微分运算的局部微小点在哪里。如果这个局部微小点在导线之外,则传导电流密度jc为零,这时坡印亭定理(7)退化为:
(10)
方程(10)仅仅是方程(7)的一个特例,其中传导电流密度jc是零。方程(10)反映了电磁波在自由空间以及绝缘介质的传输过程。在直流电路的情况,导线外的电场强度以及电场强度都不随时间变化,方程(10)的右边为0;左边坡印亭矢量的散度是0。
另一方面,如果局部微小点位于导线内部,则传导电流密度jc和E在不同位置可能是不同的。更加重要的关键点:我们必须从物理源头上搞清楚,导线内部的电场强度E和传导电流密度jc是如何产生的。这个过程需要区分二种不同的情况:
1) 如果它们是由闭合电路中电源的电动势产生的,那么这个物理过程不涉及到交变磁场产生交变电场,也就不涉及坡印亭定理。
2) 如果是电磁波传输到接收天线,在接收天线的导线内产生了电场强度E和电流密度j,那么这个物理过程需要坡印亭定理。所以,坡印亭定理(7)是有一定适用范围的。
4. RL电路中低频交流电的速度
上节中对于坡印亭定理(7)的讨论也适用于低频交流RL电路。
图2中Vs代表交流电源,L1是电路的电感,R1是电阻。对于低频交流RL电路,公式(1)中右边第2项的位移电流项的作用非常小,接近于0。导线内部的电场强度E和传导电流密度jc是由闭合电路中电源的电动势产生的,这个物理过程不涉及到坡印亭定理。
低频交流RL电路的硬件是电源、导线、电阻和电感。经典电路理论基础公式是欧姆定律以及基尔霍夫二个定律。实际电路的功能可概括为两个方面:其一,进行电能的产生、传输、分配与转换,如电力系统中的发电、输配电线路等。其二,实现低频信号的产生、传递、处理与控制,例如电话、有线电视电路等。
电路的主要物理量是电源电动势、电流和电压。电动势是表示电源性质的物理量,它可以用U来表示,其单位是伏特(V)。电源的电动势U在数值上等于电源力(非静电力)把单位正电荷从低电位端经电源内部移到高电位端所做的功。
以图2的RL电路为例,具有电阻和自感的基尔霍夫电压定律可以写出具体形式:
(11)
在式(11)中,U(t)代表电源的电动势。其中右边第1项是欧姆定律,右边第2项可以从法拉第定律推导出来。
事实上,在低频交流电的情况下,基尔霍夫电压定律是根据能量守恒定律结合了法拉第定律的严格表示式。它是与麦克斯韦方程平行发展的一个基本方程式。式(11)是基尔霍夫电压定律应用在RL电路的实例。
集总元件电路的模型忽略了电信号在电路中传播的有限时间 [8] 。但是使用现代示波器,可以测量电路中纳秒级的时间,并且在RL电路中可以推算出交流电的速度。
最近几年以来,我们用实验研究了低频交流电的速度 [9] [10] [11] [12] 。在我们的实验中,我们采用
了一长一短的二个不规则形状的RL并联电路。我们用L1和L2分别代表短导线和长导线的自感。
,是示波器的二个输入阻抗。在实验中,工作频率是2 MHz,整个电路的尺度不超过4米。短导线回路与长导线回路安排在不同的方向。在这样的电路设计中,电路长度小于等效波长(c/f)的5%,所以它是不能用“传输线理论”进行理论计算的。
为了计算一个RL电路的时间延迟,我们利用了带有电感的基尔霍夫电压定律,即方程式(11)。在我们的实验中,L1和L2分别代表短导线和长导线的分布电感,它们不是单独的电感元件。也就是说,导线的分布电感与导线长度有关。这个设计是与图2中表示的单个电感元件有明显的不同。
直导线的分布电感值由以下近似公式计算 [10] :
(12)
在式(12)中,l为导线长度,r为导线截面的半径。长度以m为单位取数值,计算结果单位是H(亨利)。通过计算,可得直径为1.0 mm,长度为0.4 m的铜导线的分布电感为530 nH;长度为6.4 m的铜导线的分布电感为11.2 mH。由于1.0 m导线的分布电感大约为1.0 mH,对于2 MHz信号,它的阻抗大约为12 Ω;6.8 m导线的分布电感为12 mH,对于2 MHz的信号,阻抗大约为150 Ω。而示波器选择的输入阻抗是1 MΩ,所以无论是12 Ω还是150 Ω,相对于1 MΩ的输入阻抗而言,均是很小的。
我们的实验数据表明,在信号频率超过3 MHz以后,示波器显示的相位出现明显的位移。这个现象很可能是由导线的电感与示波器内部的电容和电感相互作用导致的。在示波器端口的内部一般有10~20 pF的电容,这个电容以及端口附近的分布电容对于交变信号的时间延迟是有一些影响的。可是,在我们的实验中,我们关注的是二个交变信号的时间差,所以示波器端口电容的效应被减掉了。在实验过程中,我们首先交换两个示波器通道,表明交变信号无变化,这说明示波器的二个通道性能一致。
下面,我们计算一个RL电路中,电阻上的电压相对于电动势电压的时间延迟。对于一个RL电路,交变电流可以用指数形式表示
(13)
这里,j代表虚数。于是具有电感的基尔霍夫电压定律表示式(11)可以写为:
(14)
在
的条件下,式(14)可以改写成为
(15)
在式(15)中,Φ代表相位角:
(16)
所以,在RL电路中,电阻R上的电压与电动势U(t)相比较存在一个时间延迟:
(17)
这个时间延迟量与工作频率无关。如果取电感L为10 mH,电阻R为1 M欧姆,那么Dt大约是10 ps。
根据公式(12),直导线的电感值与导线的总长度正相关。如果把公式(12)的时间延迟与交流电的速度相联系,我们引入了下面的工作定义:令RL电路的回路总长度为l,它近似于导线的总长度。我们把导线中交变电场速度定义为:
(18)
对于6米长的铜导线,电感L大约为11 mH。在我们的实验中,电阻R是1 MΩ。根据公式(18),我们得到VAC的理论值:VAC ≈ 1800c,c代表真空光速值。从我们的多次测量,对于频率在3.0 MHz以下的信号,纵向电场的速度超过光速20倍以上,这个结果与频率无关。实验结果表明,交流电在金属导线中可以超光速传输信号和电能。本实验的关键是:电路的分布电容小于1 pF,可以忽略。RL电路中纵向交变电场的时间延迟是由单导线自身的电感引起的,导线自感量与长度有一定的相关性。
从我们许多次的实验表明,导线中低频交流电可以大大超光速,这是RL电路根据公式(11)得到的一个推论。
当工作频率是2 MHz时,它的等效波长(c/f)是150米,而我们实验中的电路长度小于10米。对于这样的实验室尺度内的电路实验,电路专家采用集总电路模型。集总电路模型是不计算导线长度的,其实它隐含了一个假定:交变电信号在导线中的速度是无穷大。所以我们的实验结果表明,在特定条件下交变电信号在导线中的速度超光速20倍以上,这不仅是合理的,而且也是对集总元件电路模型的改进。
5. 结论
本文讨论了坡印亭定理以及集总元件电路模型。
对于集总元件电路模型,从带有电感的RL电路的电压方程式(11),可以计算出大电阻上的电压对于电动势的相位延迟,它等价于时间延迟。这个时间延迟是由直导线的分布电感引起的。所以直导线的分布电感是“因”,大电阻上电压对于电动势的相位延迟是“果”,计算得出的交变电信号在导线中的速度可以超光速是推论。
我们强调指出,式(11)是一个标量方程。由于电源U(t)是电路中一个独立的组成部分,它是外力在电源内部对电荷做功引起的。所以,方程式(11)体现了电路的整体特性以及标量时间。
在方程式(11)中,电流I(t)以及时间变量t也是标量。它表明,对于某一时刻,在电路中不同地点,电流I(t)是相同的。它体现了异地同时性的绝对性。当时间变化时,电路中电流的大小以及相位是随时间整体变化的。所以,交流电在金属导线中由相位变化来传输信息是一种宏观的非局域性效应。“非局域”的超光速物理作用,不仅仅在量子力学领域存在,并且在宏观世界也存在。
在低频交流电路的情况,电源产生的交变电动势直接把能量和信息以纵场的形式同步地传送给电路的各个部分。这种传送能量的方式与电磁波是完全不同的。电路中的低频交变电场具有频率以及相位的特征,可是不存在波长的定义。
我们实验中测量到1纳秒级的时间差,主要归功于本世纪以来示波器技术的进步。我们的贡献仅仅是选对了实验的方法,指出了实验中电路的特定条件。时间测量的误差由示波器的精度决定。
集总元件电路的模型忽略了电信号在电路中传播的有限时间。但是使用现代示波器,可以测量电路中纳秒级的时间,并且在RL电路中可以推算出交流电的速度。典型的RL电路由电源,导线,电阻和电感组成,基本公式是方程式(11),它可以从欧姆定律和基尔霍夫定律推导出来。根据我们的实验结果,考虑到电信号传播的有限时间,集总元件电路的模型可以得到改进。
直流电能的传输过程与位移电流无关,也与坡印亭定理无关。在直流电路的情况下,电路内部的自由电子在电源的电动势的驱动下运动,电动势能转化为自由电子的动能,形成了电流。在这种情况下,坡印亭矢量只是一个数学定义,它没有形成真正的能流,所以电磁能流不是从金属导线的外部传输到内部的。
在推导坡印亭定理的过程中,用到了位移电流项以及法拉第定律。这个过程表明必须有个交变磁场产生交变电场的物理过程。这个物理过程在自由空间以及绝缘介质中的电磁波传输时存在。
在推导坡印亭定理的过程中,当把E的点积代入方程(1)的两边进行运算时,我们必须考虑我们采取微分运算的局部微小点在哪里。如果这个局部微小点在导线之外,则传导电流密度jc为零,这时坡印亭定理(7)退化为方程(10)。
另一方面,如果局部微小点位于导线内部,我们必须从物理源头上搞清楚,导线内部的电场强度E和传导电流密度jc是如何产生的。这个过程需要区分二种不同的情况:
1) 如果它们是由闭合电路中电源的电动势产生的,那么这个物理过程不涉及到交变磁场产生交变电场,也就不涉及坡印亭定理。
2) 如果是电磁波传输到接收天线,在接收天线的导线内产生了电场强度E和电流密度j,那么这个物理过程需要坡印亭定理。
无线电磁波发射的条件必须采用开放电路,而且要求频率足够高。
对于低频闭合交流电路,它不发射电磁波。然而,在低频闭合电路的周围空间,存在低频交变的电场和磁场。由坡印亭定理退化的方程(10),表明导线外的空间存在电磁场能量转换,可是没有电磁波的发射和传播。
总之,坡印亭定理是有一定适用范围的。在有电源的直流电路以及低频交流电路的情况,导线内的电能的传输过程与位移电流无关,也与坡印亭定理无关。
致谢
作者感谢褚君浩院士和殷业教授的有益讨论和帮助。
NOTES
*通讯作者。