重叠网格技术在小型油粘滞阻尼器设计中的应用研究

Overlap Grid Research on the Application of Minitype Oil Viscous Damper Design

摘要: 论文采用URANS方法和运动重叠网格计算盛液封闭容器内的薄板振动绕流问题。数值网格采用两套网格重叠布置的形式，网格运动由用户自定义函数(UDF)实现，湍流模型采用SST k-ω模型，采用有限体积法和PISO算法求解URANS方程。文中通过对带正六边形薄板的小型油粘滞阻尼器进行建模分析及求解。结果表明，这种阻尼器的耗能能力与薄板面积基本呈线性关系，与薄板振幅的平方也呈近似线性关系，一个振动周期内薄板表面压力演化过程的流场显示，有助于增进对此类流动问题的认识。计算结果还表明基于重叠网格技术的CFD数值模拟，可以较好的模拟盛液封闭容器内振动薄板的流动问题。

Abstract: Unsteady Reynolds Averaged Navier Stokes (URANS) methods and moving overlap gird tech-nique are used to calculate the internal flow around thin plate vibrating in vessel filled with vis-cous fluid. Computational grid zones are arranged overlapping each other. The gird moving is carried out by using user define function built in commercial software. The SST k-ω turbulence model, finite volume method and PISO algorithm are employed to solve URANS equations in viscous flow calculation. This paper builds numerical model for a minitype oil viscous damper with hexagon thin plat and solves the internal flow. The results show that the energy dissipation capacity of this damper is not only in linear relationship with the area of the plate but also pro-portional to the square of the vibration amplitude. The flow visualization of the pressure evolu-tion on surface of the oscillating thin plate during a period contributes to insight of flow prob-lem in this kind. Those results also manifest that the present CFD simulation with overlap gird is suitable for calculating the oscillating flow induced by thin plate in closed container filled with viscous fluid.

1. 引言

盛满液体的封闭容器内振动薄板结构的流动模拟问题是设计油粘滞阻尼器需要解决的重要研究课题，具有丰富的工程应用场景 [1] 。近些年来，随着CFD数值模拟技术的不断完善和计算机计算效率的持续提高，数值模拟在油粘滞阻尼器领域的发展很快，但网格生成和运动的模拟方法仍然是关键技术之一 [2] 。

在CFD常见使用的网格种类中，结构网格技术发展较早，具有网格生成技术成熟、数值精度高、壁面粘性力模拟效果好等优点，但其对复杂几何局域的使用能力较弱。非结构网格具备极强的几何适应能力，但其数值精度比结构网格低 [3] 。在实践工程中，计算对象构件自身的功能性决定了其往往具备不规则的几何形体，大多数时候出于缩减建模难度和建模周期，工程分析人员更倾向于是使用非结构网格建模，而代价则是计算精度的部分损失。

重叠网格技术的出现，使得复杂工程结构的结构化建模成为可能。重叠网格的基本原理 [4] [5] 是采用多套网格，将需要计算的复杂流体区域分成具有简单几何边界的计算子区域，每个计算子区域中的网格是单独生成的，各个子区域之间存在着部分或全部的重叠关系，流场基本物理量在重叠区域的边界上通过数值插值进行耦合和匹配。由于重叠网格的单个子区域是独立生成的，且可根据计算人员的设计划分成简单的规则区域，这使得重叠网格拥有结构网格流场计算精度高、计算存储逻辑关系简单高效、壁面粘性估计更准确等优点，更关键的是显著提高了结构网格对复杂几何工程对象的适应能力 [6] 。

不仅如此，将重叠网格技术与网格运动相结合，还可以克服常规动网格技术中网格重划与变形更新时网格质量蜕化的弊端 [7] ，具有强大的模拟复杂运动的能力。当重叠网格与网格运动结合时，常采用两套计算网格，一套为流体计算域的背景网格，一套为包裹被分析物体的前景网格，在计算对象运动的过程中，通过计算软件持续的实时检查背景网格和前景网格的重叠区域，并构造交界面，在此基础上求解整个流场 [8] 。

本文以某小型粘滞阻尼器中薄板内振动问题为工程分析对象，使用ANSYS软件重叠网格进行流体建模，计算获得典型振动频率和振幅条件下的流场分布，并对该振动薄板的阻尼耗能特性进行分析讨论，说明重叠网格技术在此类问题中的应用能力。

2. 小型油粘滞阻尼器模型

某小型油粘滞阻尼器构造如图1所示，封闭容器内盛满硅油，容器中心放置一块薄板，薄板通过连杆与容器外需要施加阻尼的工程对象相连，该对象通过连杆竖向运动连带着薄板上下振动，振动薄板受到粘性硅油提供的阻力，起到消耗振动能量的作用。

通过对硅油运动粘度、薄板形状、面积等参数的调整，可达到阻尼器耗能能力设计的目的。对于容器内的薄板振动问题，尚无通用的流体解析计算方法；而模型试验耗费的周期长、经费多，且不可能对大量工况均开展模型试验寻找最优参数；CFD数值模拟技术在研究此类问题中有着独特的优势。

本研究旨在阐述说明分析方法的适用性。不失一般性的，建模时封闭容器选取为方形柱体，其尺寸为0.3 m × 0.3 m × 0.6 m。核心薄板选取为正六边形，分别计算了面积0.01 m²、0.008 m²、0.006 m²、0.004 m²、0.002 m²共5个工况。

3. CFD数值计算模型

在URANS流动控制方程和SST k-ω湍流方程基础上，采用重叠网格技术进行建模分析。

3.1. URANS控制方程

直接坐标系下，对不可压缩非定常流体的NS程进行雷诺平均，得到非定常雷诺平均的NS方程(URANS)，如下所示 [9]

$\frac{\partial {\bar{U}}_i}{\partial t}+\frac{\partial }{\partial x_j}\left({\bar{U}}_i{\bar{U}}_j\right)=-\frac{1}{\rho }\frac{\partial \bar{P}}{\partial x_i}+v\frac{{\partial }^2{\bar{U}}_i}{\partial x_i\partial x_j}-\frac{\partial {\overline{{u^{″}}_i{u}^{″}}}_j}{\partial x_j}$ (1)

$\frac{\partial {\bar{U}}_i}{\partial x_i}=0$ (2)

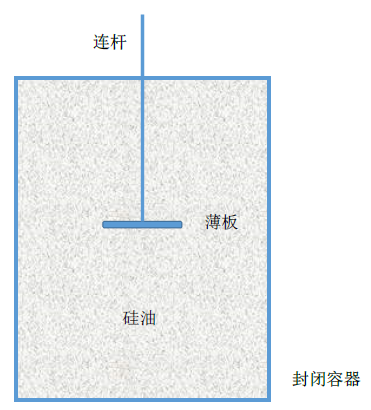
Figure 1. Vertical view of minitype oil viscous damper

图1. 小型油粘滞阻尼器立面示意图

其中

${\bar{U}}_i={\bar{U}}_i\left(x,y,z,t\right)$ (3)

$\bar{P}=\bar{P}\left(x,y,z,t\right)$ (4)

$\overline{{u^{″}}_i{u^{″}}_j}=\overline{{u^{″}}_i{u^{″}}_j}\left(x,y,z,t\right)$ (5)

式(1)为动量方程，式(2)为连续方程。该方程组存在封闭问题，需要引入湍流模型才能对其进行封闭求解。

3.2. SST k-ω湍流模型

SST k-ω湍流模型即剪切压力传输k-ω模型，是标准k-ω模型的升级版，由Menter提出 [10] ，其流动控制方程如下

$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\frac{\partial }{\partial x_j}\left({\Gamma }_k\frac{\partial k}{\partial x_j}\right)+G_k-Y_k+S_k$ (6)

$\frac{\partial }{\partial t}\left(\rho \omega \right)+\frac{\partial }{\partial x_i}\left(\rho \omega u_i\right)=\frac{\partial }{\partial x_j}\left({\Gamma }_k\frac{\partial \omega }{\partial x_j}\right)+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }$ (7)

式(6)为湍动能输运方程，式(7)为比耗散率输运方。Γ_ω、Γ_k为有效扩散项，G_k、G_ω为生成项，Y_ω、Y_k为发散项，D_ω代表正交发散项，S_ω、S_k为源项。

3.3. 边界条件与网格生成

图2所示为数值计算域，方形柱体内壁的6个表面均为无滑移壁面。正六边形型实心薄板居中布置，板厚4 mm，其表面也为无滑移壁面。薄板上下运动设为简谐运动，通过ANSYS Fluent预留的程序接口，编写用户自定义函数(UDF)来实现，振动幅值取为0.02 m，振动频率为5 Hz。流动介质需手动输入参数，硅油密度取963 kg/m³，硅油运动粘度50 cs，动力粘度为0.04815 kg/ms⁻¹。

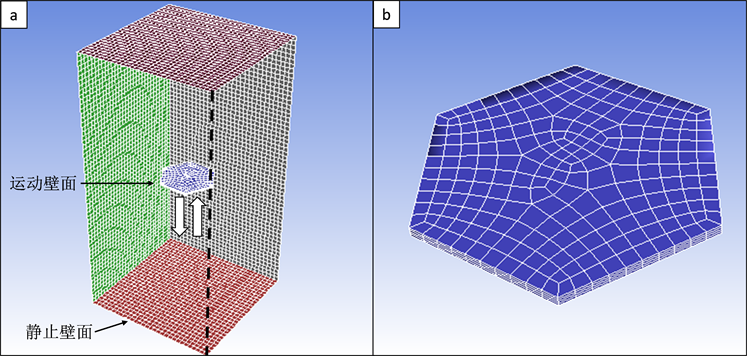
Figure 2. Boundary condition of computational domain and the surface grid of thin plate

图2. 数值计算域边界条件与薄板表面网格划分

本研究采用1套固定背景网格和1套运动前景网格的组合方案。方形柱体容器作为背景网格，按立方体结构网格铺设，网格边长0.01 m，共生成54,000个背景网格。薄板建模于前景网格中，上下表面先采用四边形非结构网格铺满，再按沿法向拉伸生成规则的棱柱体网格，薄板表面布置规则的边界层网格，贴体网格厚度1 mm，共生成82,840个前景网格。网格切片见图3，其中可见背景网格与前景网格的重叠。

计算时采用PISO方法处理压强和速度耦合，空间离散格式均为二阶精度。非定常计算的时间步长为0.002 s，每个时间步内最大迭代步数为30，残差收敛准则均为10⁻⁶。

4. 结果分析与讨论

4.1. 阻力时程与滞回曲线

图4(a)所示为薄板形心竖向运动的位移时程曲线，振幅基本为0.02 m，为较为理想的简谐曲线，可

Figure 3. Slice of the overlap grid

图3. 重叠网格切片图

见UDF函数编写正确。图4(b)所示为振动薄板受到粘性硅油的作用力，即阻尼器需要的阻尼力。从零时刻开始，阻尼力经历了一次短暂的跳跃，这是由于数值计算的初始数值迭代产生的，属于数值意义上的求解过程数据，不对应实际的物理过程。随后，阻尼力进入了绕零轴附近波动的状态，且峰值逐渐趋于稳定。至1.5 s后，薄板受到的阻尼力进入了等幅振荡的状态，表明此时在平板周期等幅振动的扰动下，容器内的硅油流场也已进入了周期振荡，此时视为阻尼器的有效工作状态。

薄板一个运动周期内的阻尼耗能特性可以通过滞回曲线来描述，见图5。从图中可以看出，阻尼器的位移-阻尼力滞回曲线为逆时针方向，说明硅油提供的粘滞阻尼器阻尼力对振动薄板的总做功效应为负，即起到阻尼耗能的作用。从图中还可以看出，当运动位移为零时(简谐运动此时速度最大)，硅油反馈的阻尼力并非最大，说明该阻尼力与运动速度不呈线性关系，不属于线性粘滞阻尼的类型。在一个运动周期内，阻尼力消耗的能量大小等于图中的滞回曲线面积，图5中滞回曲线表明，薄板面积越大，其阻尼耗能的能力越强。

对滞回曲线进行数值积分，得到不同面积薄板单个振动周期内的阻尼耗能，并对其关于薄板面积参数进行线性拟合，如图6所示。从图中结果可以看出，振动薄板做功耗能大小基本与其面积呈线性关系，

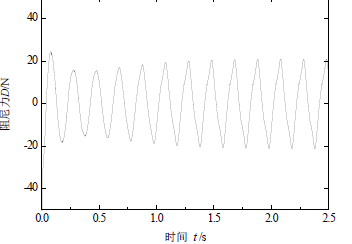(a) (b)

Figure 4. Time history of displacement and drag force

图4. 位移时程与阻尼力时程(面积A = 0.01 m²，振幅h₀ = 0.02 m)

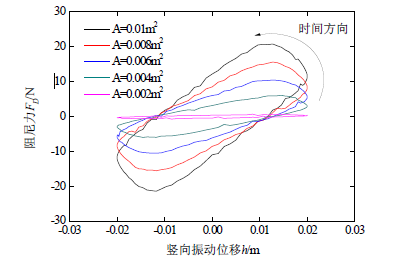
Figure 5. Displacement-drag hysteretic curves of the vibrating thin plate with different area when the amplitude is 0.02 m

图5. 不同面积振动薄板的位移-阻尼力滞回曲线(振幅h₀ = 0.02 m)

这一规律可用于指导阻尼器前期初步设计时的薄板参数选取。

4.2. 薄板表面压强演化

针对正六边形薄板面积为0.01 m²、振幅为0.02 m的工况，使用CFD流场显示技术，取薄板通过平衡位置向上为零时刻，提取薄板在一个运动周期内9个典型时刻(见图7)的表面压力分布。由于薄板为上下对称结构，其运动具有周期的特征，上下表面的压强应具有半周期时间平移的重现的特征，故仅绘制了薄板上表面的压力云图如图8所示。

从图8中可以看出，当薄板通过平衡位置向上运动时(t = 0)，此时运动速度最大，上表面受较大的正压作用，压强分布比较均匀，其平均压力值约为850 Pa。当薄板向上运动至最高位置时(t = T2/8)，此时运动速度为零，上表面受负压作用，其最大负压出现于薄板边缘，上表面中心大部分区域负压分布基本均匀，约为−1200 Pa。当薄板通过平衡位置向上运动时(t = T4/8)，此时运动速度也达到最大，上表面受到更强的负压作用，最大负压仍然位于薄板边缘，但上表面中心大部分区域负压值增加为约−2300 Pa。

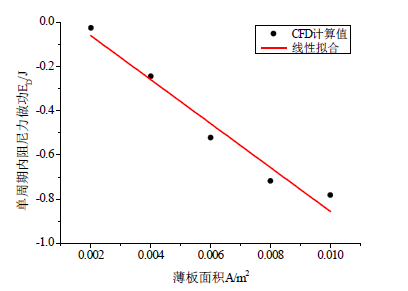
Figure 6. Damping dissipation energy in a period of the vibrating thin plate when the amplitude is 0.02 m

图6. 振动薄板面积与单个振动周期内阻尼耗能关系曲线(振幅h₀ = 0.02 m)

Figure 7. Schematic diagram of the specified moment during a period

图7. 单个运动周期内的典型时刻示意图

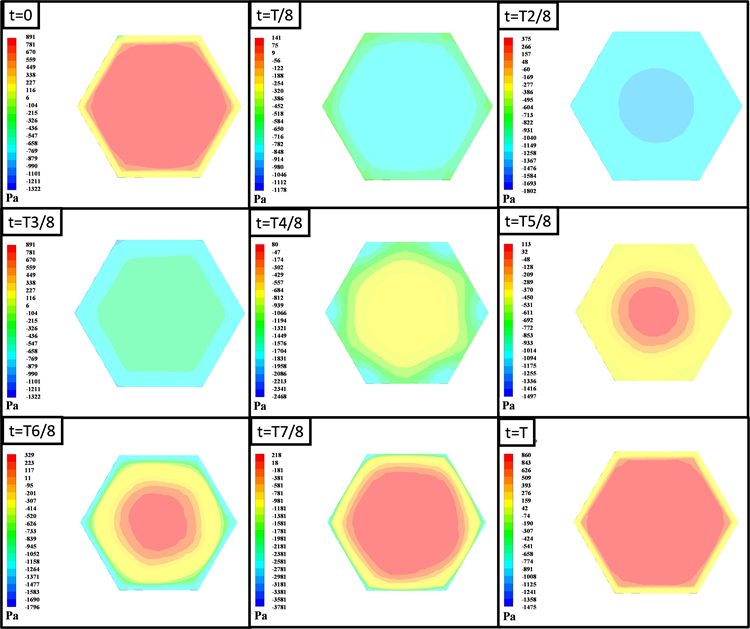
Figure 8. Evolution of the pressure acting on upper surface of the thin plate during a period displayed by filled contour line

图8. 一个振动周期内薄板上表面压力云图演化(面积A = 0.01 m²，振幅h₀ = 0.02 m)

随着薄板继续向下运动至最低位置时(t = T6/8)，此时运动速度为零，上表面中心区域受正压作用，边缘区域受负压作用，越靠近中心正压强越大，最大正压约为330 Pa，越靠近边缘负压强越大，在较大范围内负压约为−400 Pa。当薄板从最低位置向平衡位置恢复时，其上表面负压区逐步缩小，正压区逐渐扩大，直至再次达到平衡位置时(t = T8/8)，上表面再次受到较为均匀的正压作用。

4.3. 薄板振幅的影响

阻尼器的工作对象往往在一定的振幅范围内振动，需要考察其在不同振动幅值水平下的阻尼特性。为此，在保持振动频率不变的前提下，针对薄板面积为0.01 m²的情况，计算了0.005 m、0.01 m、0.015 m、0.02 m、0.025 m、0.03 m共6个振幅条件下的阻尼情况。

图9所示为不同振幅水平下的振动薄板的位移-阻尼力滞回曲线。从图中可看出，小振幅条件下，滞回曲线较为光滑，此时薄板的最大瞬时速度较小，其对流场的扰动相对弱，流场中粘性力占主导优势。随着振幅的增大，滞回曲线表现出区部波动，大振幅薄板的最大瞬时速度较大，可能引起板后局部区域发生流动分离形成漩涡，造成薄板整体受力的波动。此外，滞回曲线形成的封闭滞回环的长轴随着薄板振幅的增大，呈现朝逆时针方向转动的趋势，这也反应了不同振幅水平下流场振荡相对于薄板振荡的滞后程度发生了变化。

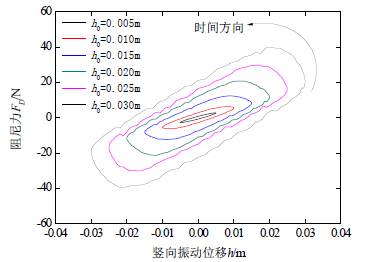
Figure 9. Displacement-drag hysteretic curves of the vibrating thin plate with different amplitude when the area is 0.01 m²

图9. 不同振幅振动薄板的位移-阻尼力滞回曲线(面积A = 0.01 m²)

Figure 10. Function fitting between the damping dissipation energy and the vibration amplitude of thin plate

图10. 阻尼耗能与薄板振幅的函数关系拟合

图10所示为计算得到的不同振幅条件下在一个振动周期内振动薄板所受到流体阻尼力做功的量，并将该部分阻尼耗能与薄板振幅的关系进行多项式函数拟合。通过对比可以发现，线性拟合的结果很不理想，而二次(或更高次的)拟合则可以达到0.995以上的拟合度，这说明了这种阻尼器的耗能能力基本与薄板振幅的平方呈线性关系，使得其在结构动力学上基本可以视为等效线性的粘滞型阻尼器，这一规律可以为该类阻尼器满足不同耗能大小的工程(或教学)需求提供设计参考。

5. 结论

本文初步尝试采用重叠网格方法结合网格运动技术，利用URANS方程和SST k-ω湍流模型成功地数值模拟了盛液封闭容器内振动薄板的流场计算问题。尽管在现阶段受试验条件的限制，计算结果未与试验结果进行对比验证，但从理论分析来看，数值模拟结果基本符合此类流动的一般特征，是比较合理的，后期亦将开展基于其它方法的数值计算进行对比验证。

重叠网格运动技术是一种实用的工程容器内振荡流CFD方法，其在复杂流场网格结构化建模方面有着独特的优势，是未来工程流体计算领域内的一个重要研究方向。我们后期目标是应用该方法对该类小型粘滞阻尼器进行参数优化分析，最终达到服务设计之目的。

基金项目

西南石油大学大学生创新创业训练计划项目(20160615100)；西南石油大学科研启航计划项目(2017QHZ024)资助。