1. 引言
粒子的自旋禀性有着广泛的应用前景,如核物理中的核结构研究、医学核磁共振成像、军事与民用原子导航等。粒子自旋与库仑力一样都是其内禀特性,原子结构、核结构甚至核力等均与粒子自旋相关,因此在粒子的相互作用中自旋的影响实际上往往不可忽略。核物理研究中十分重视核反应截面及反应概率的研究,自旋对核反应截面及概率的有影响国内外均有认知,但长时间内都缺乏不依赖于实验数据的理论分析模型与相应实验手段,目前世界上只有美国布鲁克海文实验室的相对论重离子对撞机(RHIC)带有极化功能,可进行高能极化对撞实验,但对中、低能区尚缺乏验证手段。国内对于极化对撞的研究从公开文献看是十分稀少的,采用的数据均来源于国外,国内的实验研究尚处于空白阶段。
本文以氢核(质子)为例讨论自旋对核反应截面与核反应概率的影响,首先基于量子学与磁学建立了质子的磁荷模型,便于进行磁力分析,然后推导了全极化p-p对撞实验与未极化p-p对撞实验中核反应事件数之比及其核反应截面增量的简明表达式,并基于实验数据对模型进行了验证,通过对比发现文中给出的模型是有效的,可在缺乏实验数据的情况下对极化核反应的预期结果进行较为精确的估算,有实用价值。
2. 理论模型
氢原子模型中,质子只受到核外电子的库仑力、自旋与轨道运动引起磁力作用,由于电子轨道稳定,电子所受到的各种互作用是平衡的,质子亦然。需要说明的是,电子的磁相互作用能不是与库仑互位能相平衡,而是不能大于其轨道能级,否则电子将发生跃迁,也即轨道能级是氢原子中电子与质子间磁互作用能的上限 [1] ,本文使用的氢原子模型如图1所示。
质子在电子磁场中的磁相互作用能为 [1] [2] [3]
(1)
式中
为核磁子,
,B为电子自旋与轨道运动在质子处产生的磁场。
WM可取值为所有氢原子能级精细结构
中值最小的 [4] 。因此,核外电子自旋与轨道运动在质子处产生的磁场为
(2)
由于自旋与轨道运动为质子的内禀特性,磁矩的存在会使质子对电子产生的磁场有响应,即质子会如永磁体一般在磁场中受到磁力作用,质子可视为带有磁荷qm的永磁体,根据磁荷理论,质子磁荷产生的磁
场为 [5]
(3)
r可取为波尔半径,即
,该场可视为核外电子磁场在质子上的感应场,即
(4)
结合(1)、(3)式,则有
(5)
由上式可推导出质子的磁荷为
(6)
对于自由态的质子,由磁荷理论,两质子磁荷间的磁力大小为
(7)
而两质子间的库仑力大小为
(8)
为真空磁导率和介电常数。因此可导出自旋磁力与库仑力之比为
(9)
基于基本物理常数,公式(9)说明质子自旋磁力在数值上是大于库仑力的,但根据磁极取向不同,实际中会产生不同的效果,如磁极异性,则磁力为引力,可以克服库仑斥力,电荷间总的作用力表现为引力,如果磁极同性,则磁力是斥力,电荷间总作用力也表现为斥力,且这个合力的数值大于应有的库仑斥力。在这里,我们感兴趣的是第一种情况,下面继续进行讨论。
如图2所示,质子对撞过程中,假设入射质子动能足以克服库仑势垒,那么在自旋磁引力不起作用的情况下,只有o点的直入射质子可以击中位于d电的质子,如果计及自旋磁力作用,且质子间的作用力表现为引力(即磁极异性对撞),则从以Ra为半径的圆环上以初速V0出射的质子会在引力作用下沿轨迹
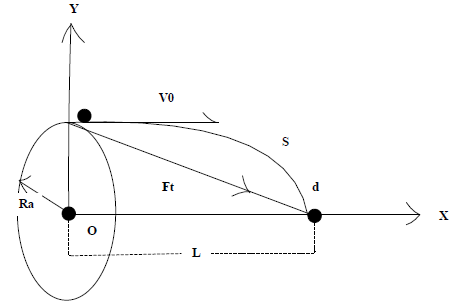
Figure 2. Sketch of particle motion under self-spinning magnetic gravity
图2. 自旋磁引力作用下粒子运动示意图
S运动后也击中d点质子,即在磁引力作用下反应概率会有所提高,Ra可定义为全极化条件下自旋引力的作用半径。令
,δ为磁作用力超出电作用力的比例系数。当圆环上入射的质子能量为E0时,其x向位移与y向位移大致有如下关系
(10)
式中,mp为质子的静质量,此时对撞质子间的合力可表示为
(11)
进一步当x = L (L为对撞区尺寸),y = Ra时,有
(12)
令质子能量为
,最终可导出自旋磁引力半径Ra的表达式为
(13)
设原子核间距为两倍波尔半径2r,那么核反应事件数为
,即圆环上的粒子数与o点质子数之和,而非极化状态下该数仅为1。因此,全极化状态p-p对撞与非极化状态p-p对撞的核反应事件数目之比ζ可近似为
(14)
核反应概率定义为
(15)
式中N为靶核数,x为入射质子在靶中的穿透深度,定义未极化状态与极化状态的核反应概率分别为P1、P2,核反应截面为
、
,则有
(16)
经进一步推导,有
(17)
此即核反应截面增量与反应概率比值之间的关系,而未极化状态下的核反应截面
有实测数据可采用。
公式(7)、(9)可用于质子的磁互作用力计算及p-p对撞时质子间合力计算,公式(13)、(14)、(17)则可用于核反应事件数目、反应概率比值与核反应截面增量的计算,这些公式都是显式的简明公式。
3. 算例
3.1. 模型校验
首先基于美国布鲁克海文实验室RHIC高能质子极化对撞实验数据对本文的模型进行校验,在文献 [6] 中,给出了核反应事件数的测试值,本文计算结果与实验数据的对比如图3所示,质子能区为2.0~2.5 GeV。
通过对比可以发现本文计算结果与实验结果处于同一量级,且核反应事件的数目随能量上升均呈现递减趋势,实验结果在2.15 GeV处存在一突变峰值,而仿真结果是单调衰减的,经分析误差产生的原因包括:1) 模型误差,建立的模型和真实物理本质之间存在偏差,而模型未能很好的计及相应因素;2) 极化率的影响,这个影响因素十分明确,本文建立的是全极化模型,而文献中质子束极化率处于0.6~0.9之间,极化率与核反应事件数呈1/3次方关系,其引起的误差在5%~7%之间;3) 实验误差,文献中对实验的细节没有充分强调,实验环节中也可能存在误差。计算结果与实验结果在整个能区上的(正负)误差分布如图4所示,大部分能区误差处于10%以内,只有2.15 GeV处误差达到24%,扣除极化率误差,大部分
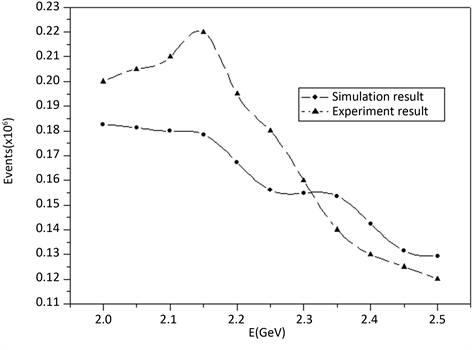
Figure 3. Comparison between the calculated results and RHIC experimental data
图3. 本文计算结果与RHIC实验数据的对比
能区上误差可控制在5%以内。因此,本文的模型是有相当高的可信度的。
3.2. 自旋引起的反应截面增量分析
本例我们分析全极化情况下核反应截面、核反应事件数相对于未极化状态时的增量,考察极化在核反应中所带来的收益。图5是300~1200 MeV能区未极化状态下的p-p核反应截面 [7] ,应用本文模型计算所得的全极化条件下核反应截面增量如图6所示,与之对应的核反应事件比值数如图7所示。
通过计算结果可以发现,在全极化条件下,p-p的核反应概率可提高三个数量级,对应的核反应截面增量也在同一量级。
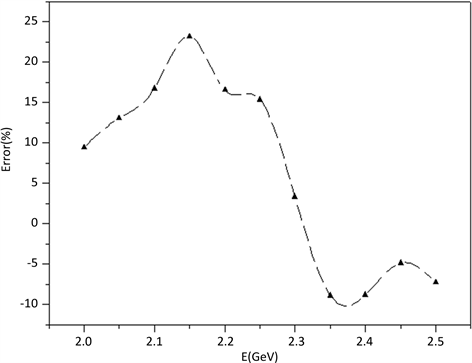
Figure 4. The error curve of experimental data
图4. 与实验数据的误差曲线
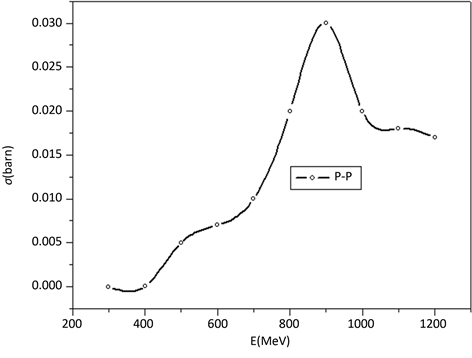
Figure 5. p-p scattering cross section in unpolarized state
图5. 未极化状态下p-p散射截面
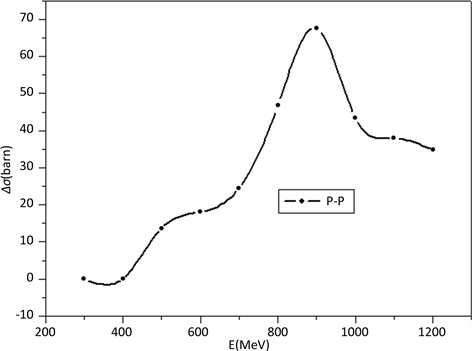
Figure 6. p-p scattering cross section in polarized state
图6. 极化状态下p-p散射截面
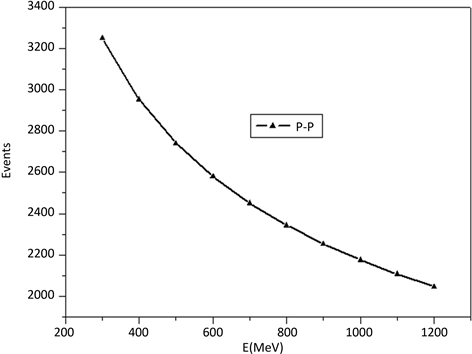
Figure 7. p-p nuclear reaction event in polarized state
图7. 极化状态下p-p核反应事件
3.3. 自旋对低能区反应概率的影响
最后,对低能核反应进行分析,由于缺乏低能p-p核反应截面数据,因此这部分的讨论仅仅局限于极化对于核反应概率的影响。图8给出了10 MeV以下能区p-p全极化对撞的核反应事件比值数据,反应概率可以提高四个数量级。
4. 结束语
本文将质子等效为同时带有电荷和磁荷的粒子,推导了全极化状态下核反应事件增比与核反应截面增量的简明表达式,以便于工程上的快速预测,模型尚不完善,有待后续进一步改进,本文想要强调的
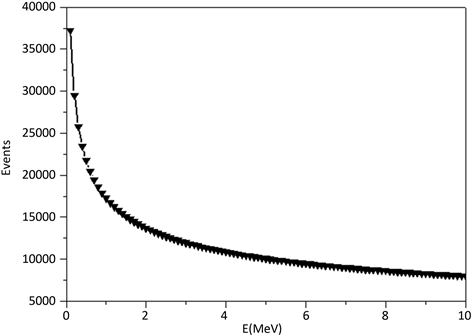
Figure 8. The relationship between the incident nuclear events and the incident proton energy in the low energy region
图8. 低能区核事件与入射质子能量的关系
是原子核拥有库仑与自旋特性,自旋对于核反应的影响不容忽略,合理的利用自旋,对于提升核反应截面(概率)是有益的,通过本文的分析发现,自旋可以用于克服(至少是有效降低)核反应时的库仑势垒,而且规律是质子能量越高,自旋的这种影响越弱,例如在低能区全极化可以使核反应概率增长四个数量级,随着质子能量升高,反应概率的增比反而降低。目前国内尚未开展极化核物理实验研究工作,基础实验数据十分缺乏,希望国内研究机构及团队能在这一领域尽快开展工作。