1. 引言
国内生产总值(GDP)是国民经济核算的核心指标,同时也能很好的衡量一个国家或者地区的国民经济经济发展水平和宏观经济运行状况的重要指标,分析预测国内生产总值(GDP)走势,已经成为政府制定宏观经济政策及宏观经济决策的重要依据和参考。1970年,Box和Jenkins在其联合编著的《Time Series Analysis:Forecasting and Control》一书中,在前人研究的基础上,提出了求和自回归移动平均(ARIMA)模型,系统的阐述了如何对ARIMA模型进行识别、估计、检验以及预测的原理和方法。本文试图利用ARIMA模型对1978至2017年宿州市国内生产总值(GDP)进行分析和建模,并且利用建立的模型对2017年至2020年的国内生产总值(GDP)进行预测,以期为宿州市委市政府制定经济发展目标提供参考。
2. ARIMA模型的结构
ARIMA模型本质上就是差分运算与ARMA模型的组合。考虑非平稳序列
,如果该非平稳序列能通过d次差分后变为平稳序列,则满足如下结构的模型称为ARIMA(p,d,q)模型:
式中,
为平稳可逆ARMA(p,q)模型的自回归系数多项式;
为平稳可逆ARMA(p,q)模型的移动平均系数多项式 [1] 。
3. ARIMA模型的建立与检验
3.1. ARIMA模型建立的方法
通过图1的建模流程,我们可以建立ARIMA模型,实现对非平稳时间序列的建模分析。
3.2. 数据的来源与描述
从《宿州五十年》、《宿州统计年鉴》各卷摘取1978至2017年宿州市国内生产总值,见表1。并根据数据作出图2,从中可以看出宿州市GDP序列具有明显的增长趋势,由图3可以看出自相关系数缓慢递减到零,而后变为负值,结合图4显示可以判断宿州市GDP序列为具有增长趋势的非平稳序列。
3.3. 序列的平稳化处理
对于非平稳时间序列,我们往往利用差分使其转化为平稳时间序列。我们对该序列先使用一阶差分,并选用ADF单根检验确定差分序列的平稳性。观察图5所示一阶差分序列,可以看出该序列仍有明显的
增长趋势。在显著性水平取.05时,通过表2,可以看出ADF单根检验结果p-Value > 0.05,可以看出宿州市GDP一阶差分序列为非平稳序列 [2] [3] 。
我们再次对宿州市GDP序列进行差分运算,即图6。从二阶差分序列图可以粗略看出,宿州市GDP二阶差分序列是平稳的,ADF单根检验结果显示,在显著性水平取0.05时,该序列是平稳的,见表3 [4] 。
3.4. 模型建立与检验
由以上对于宿州市GDP序列的平稳化处理,我们可以确定ARIMA(p,d,q)模型中的参数d为2。为了

Table 1. Statistical table of Suzhou's gross domestic product (GDP) from 1978 to 2017 (100 million yuan)
表1. 1978~2017年宿州市国内生产总值(GDP)统计表(亿元)
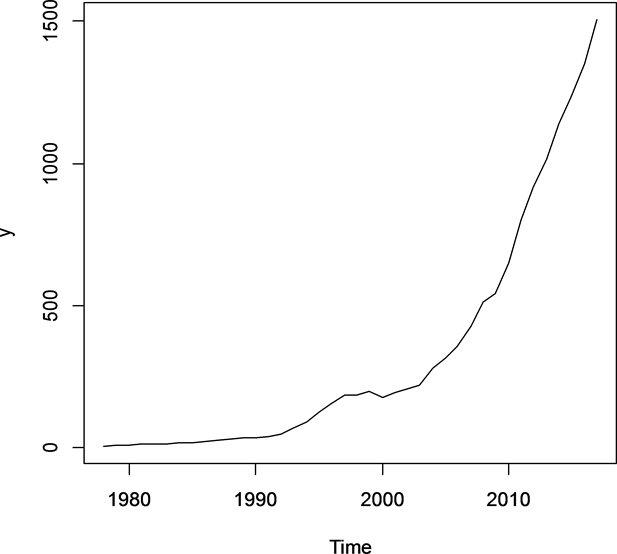
Figure 2. Suzhou’s gross domestic product (GDP) time series from 1978 to 2017
图2. 1978~2017年宿州市国内生产总值(GDP)时序图

Figure 5. Time series first-order differential
图5. 时间序列一阶差分图

Figure 6. Time series second-order differential
图6. 时间序列二阶差分图

Table 2. ADF Single root test results of Suzhou’s GDP first-order differential sequences
表2. 宿州市GDP一阶差分序列ADF单根检验结果

Table 3. ADF single root test results of Suzhou’s GDP second-order differential sequences
表3. 宿州市GDP二阶差分序列ADF单根检验结果
确定模型中参数p,q,我们观察宿州市GDP二阶差分序列的自相关图和偏相关图。
由图7和图8可以看出,该序列的自相关图和偏相关图都是拖尾的,因此可以建立ARIMA模型。
R软件提供了auto.arima()函数,我们可以参考auto.arima()函数定阶,结合GDP二阶差分序列ADF单根检验结果,建立备选模型ARIMA(1,2,1)、ARIMA(2,2,1)、ARIMA(0,2,1)、ARIMA(1,2,2)、ARIMA(2,2,2)和ARIMA(0,2,2) [4] 。
为确定模型拟合的有效性对上述备选模型进行显著性检验即残差序列的纯随机检验,见表4。
LB统计量p-Value均显著大于0.05,可以知道残差序列通过了纯随机性检验,即认为以上模型显著有效 [5] 。
3.5. 模型优化
对于同一个序列我们构造了6个显著有效拟合模型,为了进一步确定最优拟合模型,我们依据AIC信息准则(Akaike information criterion),参考对数似然值(Log likelihood)对以上6个模型进行筛选,见表4 [6] [7] 。

Figure 7. Second-order differential ACF
图7. 二阶差分序列自相关图

Figure 8. Second-order differential PACF
图8. 二阶差分序列偏相关图
从表4可以看出,ARIMA(2,2,2)模型使得AIC值最小,为349.13,且对数似然值对最大,为−169.57。因此ARIMA(2,2,2)模型为相对最优模型 [8] [9] 。
4. 模型的预测
利用建立的ARIMA(2,2,2)模型对宿州市2018~2020年三年GDP进行预测,预测结果见表5。

Table 4. Suzhou’s GDP sequence model significance test results
表4. 宿州市GDP序列模型显著性检验结果

Table 5. Using ARIMA (2,2,2) to predict the GDP results of Suzhou from 2018 to 2020
表5. 利用ARIMA(2,2,2)预测2018-2020年宿州市GDP结果

Figure 9. Second-order differential PACF
图9. 二阶差分序列偏相关图
5. 结论
1) 从图9可以看出,未来三年宿州市GDP会保持平稳快速增长,增速略有下降,这与我国经济发展从高速发展转向高质量发展确实基本吻合,宿州市GDP保持中高速增长水平于现阶段宿州市为欠发达地区的发展实际相一致。
2) 通过对宿州市1978年至2017年GDP序列进行分析和建模,可以说明ARIMA模型在拟合非平稳时间序列时具有很好的效果。本文所建立的ARIMA(2,2,2),可用于宿州市GDP的短期预测,为宿州市制定经济发展目标提供参考。
附录
R语言编程程序
x<-read.table(E:/R/GDP.csv,sep=,header=T)
y<-ts(x$gdp,start=1978)
plot(y)
acf(y)
pacf(y)
y.dif<-diff(y)
plot(y.dif)
library(fBasics)
library(fUnitRoots)
for(i in 1:3)print(adfTest(y.dif,lag=i,type=c))
y.diff<-diff(y.dif)
plot(y.diff)
for(i in 1:3)print(adfTest(y.diff,lag=i,type=c))
acf(y.diff)
pacf(y.diff)
library(zoo)
library(forecast)
auto.arima(y)
y.fit1<-arima(y,order=c(1,2,1))
y.fit1
for(i in 1:2)print(Box.test(y.fit1$residual),lag=6*i)
y.fit2<-arima(y,order=c(2,2,1))
y.fit2
for(i in 1:2)print(Box.test(y.fit2$residual),lag=6*i)
y.fit3<-arima(y,order=c(0,2,1))
y.fit3
for(i in 1:2)print(Box.test(y.fit3$residual),lag=6*i)
y.fit4<-arima(y,order=c(1,2,2))
y.fit4
for(i in 1:2)print(Box.test(y.fit4$residual),lag=6*i)
y.fit5<-arima(y,order=c(2,2,2))
y.fit5
for(i in 1:2)print(Box.test(y.fit5$residual),lag=6*i)
y.fit6<-arima(y,order=c(0,2,2))
y.fit6
for(i in 1:2)print(Box.test(y.fit6$residual),lag=6*i)
y.fore<-forecast(y.fit5,h=3)
y.fore