基于连续离散问题联合求解和群组分析的多目标跟踪技术研究

Multi-Object Tracking Based on Continuous-Discrete Problem Solving and Group Analysis

摘要: 多目标跟踪技术通过对不同目标之间的相互社会关系进行建模，改善单个目标的跟踪性能，并且快速检测和预判场景中可能发生的群体类突发事件。现有的多目标跟踪技术虽在数据关联和轨迹估计上取得平衡，但依然存在诸多问题。本文介绍通过背景建模提取出的场景信息分析并识别目标来约束多目标跟踪，将数据关联和轨迹估计这两个连续和离散的经典子问题结合到统一的框架中求解；与此同时，还提出了基于群组聚类的行为建模策略，得到的语义信息提供相邻目标和轨迹之间的约束，有助于改善跟踪结果。实验表明，本文提出的策略相比经典的多目标跟踪算法准确性更高。

Abstract: Multi-object tracking technique can improve the tracking performance of a single target by mod-eling the mutual social relationship between different targets, and emergencies groups were quickly detected and predicted scenarios that may occur. Although the existing multi-object tracking technology can balance the data association and trajectory estimation, there are still many problems. This paper introduces the scene information extracted from the background modeling and object recognition to constrained multi-target tracking, and combined into a unified framework for solving with the data association and track estimation of both discrete and continuous classic sub-problems; at the same time, we propose the behavior modeling strategy based on group clustering, whose semantic information places the restriction between adjacent target and its track, which can help improve the trace results. The results of the experiment show that the proposed method is more accurate than the classical multi-target tracking algorithm.

1. 引言

多目标跟踪技术是一种能在视频序列中检测出具有某种特征的目标，并确定其大小位置以及运动轨迹的技术。近年来，随着监控技术的不断发展，多目标跟踪技术在民用和军事方面都有着非常广泛的应用。该技术不仅能够对单个目标的社会行为和运动规律进行分析，而且还能够对不同目标之间的相互社会关系进行建模，从而在改善单个目标的跟踪性能基础上，快速检测和预判场景中可能发生的群体突发事件，对于提高智慧安防监控的自动化和智能化水平具有重要意义。

2. 相关研究

多目标跟踪是这几十年来计算机视觉领域的一大热门研究课题，其相关研究在近些年里取得了显著的进步。许多现有的多目标跟踪方法较为依赖于目标检测的结果，即目标在每一帧中通过目标模型独立地进行表示，并在某些情况下结合在线模型来处理光照和外观变化。当跟踪单个目标时，目标跟踪相当于拟合一条满足时域一致性的目标运动轨迹。当同时跟踪多个目标时则因为需要考虑数据关联的问题而变得更加困难，这不仅需要给每个目标分配一个ID，而且还需要对所有目标的运动模式以及目标检测结果的分配同时进行估计。将每个检测结果进行类别标注是在离散域进行的，并且相同的检测结果仅能有一个标签。然而，在时域上的目标位置描述则是在连续状态空间中进行描述的，其还包含了目标的颜色，纹理，尺寸和速度等先验信息。可见，多目标跟踪中的数据关联和轨迹估计这两个不同的子问题是紧密耦合的。

现有的多目标跟踪技术根据其发展可以大致分为两大类。第一类方法仅依赖于过去图像帧的信息来对当前的状态进行递归式估计。早期的卡尔曼滤波方法仅能对目标的线性运动进行建模 [1]，近期越来越多基于采样的滤波器，比如粒子滤波器 [2]等能够求解更为复杂的多模态后验概率。然而，当在精确地近似复杂条件下后验概率的粒子数目快速增加时算法则将会变得难以求解。第二类方法允许某种程度的延迟并且在一个给定的时间窗口中来全局地预测所有的目标轨迹。在这种情况下，会将最优化问题约束到一个有限状态空间中进行求解，即对所有可能的目标位置集合施加约束，比如要求所有轨迹均穿过一个个单独的目标检测结果 [3]或者预先计算得到的Track let集合 [4]。那么，最优解能够在将目标检测结果和Track let进行连接基础上通过能量最小化的方式得到。在一类略微不同的方法中 [5]，候选的目标轨迹集被预先计算，那么可在轨迹层通过求解二次布尔问题将其精简到一个最优的轨迹子集。另一类降低复杂度的方法则是将跟踪区域划分成一个个不连续的且局部全连接的单元。目标的运动通过二进制变量对上述单元进行描述，并通过LP松弛法来获得全局最优解。与上述方法均不同的是，有的方法虽然同属于非递归的方法，但是将所有的离散变量松弛到一个完全的连续状态空间中 [6]。不过，其将导致能量最小化的问题变成高度非凸的优化问题，从而容易陷入局部最小值中 [7]。

综上所述，现有的多目标跟踪技术通过不同的方式在上述两个子问题上取得平衡。一类方法聚焦于数据关联问题，并使用离散优化算法来对该NP困难问题进行求解。然而，这导致了目标轨迹预测的连续性上出现问题，这不仅是由于轨迹需要在数据关联之前先被计算，而且轨迹在空域上是离散的。另一类方法则聚焦于在一个连续状态空间中对轨迹进行估计，但是将数据关联限制在仅从预先计算得到的标签集中进行选择。基于采样的方法虽然尝试将上述离散和连续问题联合起来分析，但是在模型的合理构建和求解上依然存在诸多问题。

近年来，多目标跟踪技术在纯粹的视觉信息基础上深入分析了目标的社会行为特性。通过相邻时间间隔的相似外观 [8]或者根据构建的实时模型 [9][10][11]来进行多目标跟踪，此外人群可以根据相似的运动趋势由不同的组构成，组内部的个体间在一定程度上存在空间依赖性和行动一致性，通过对群组进行行为分析可为目标跟踪提供有用的辅助预测信息 [12][13][14]，把行为分析加入到模型中可以降低数据关联时信息的歧义性 [15]。

3. 算法概述

如何将数据关联和轨迹预测这两个问题更好地联系起来分析是多目标跟踪最为关键的技术难题，为此，本文的创新点主要体现在以下两个方面：

1) 把多目标跟踪问题看作一个连续-离散的联合求解问题，实现数据关联和轨迹预测两大子问题的同步优化。将数据关联和轨迹预测这两个不同但紧密耦合的问题融合到统一的框架中实现递归式联合求解，并在结合微观社会行为分析的基础上利用标签代价函数对不合理的目标轨迹进行惩罚。

2) 在连续离散联合求解的框架基础上，增加目标组的行为建模，多个近邻的目标之间通常具有相似的位置，走向和速度等动力学特征，从而在一定的时域和空域中构成相对稳定的组。根据一种自底向上的分级聚类策略来测度场景中稳定存在的组，通过对组的外观和运动进行分析将有助于改善目标的数据关联和轨迹估计(图1)。

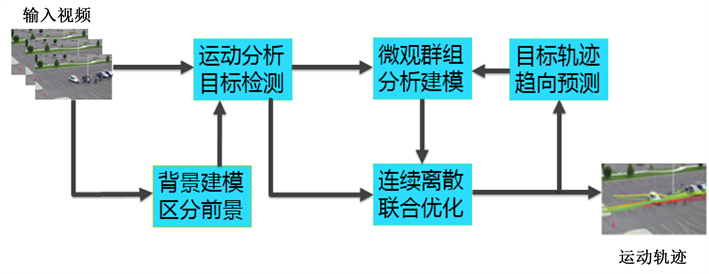
Figure 1. The implementation framework of multi-target tracking technology in this paper

图1. 本文多目标跟踪技术的实现框架

4. 连续离散联合求解算法

4.1. 背景建模与运动分析目标检测

通过对从摄像头获取或者现成的视频图像序列进行分析，将视频图像中的每一个像素点看作是产生像素的随机过程，使用混合高斯背景模型方法，利用像素在较长时间内大量样本值的概率密度等统计信息来表示背景，根据统计差分进行目标像素判断，可以对复杂动态背景进行建模，按照图像中的每一个像素点按不同权值的多个高斯分布叠加建模，得到的序列经过图像形态学处理后达到区分目标和背景的效果 [16]。

4.2. 连续离散问题联合求解

连续离散问题联合求解最开始是由Anton Andriyenko [17]提出的，通过递归的方式最小化能量函数来实现数据关联和轨迹预测的同步优化求解。能量函数由数据项、平滑项和多个标签成本约束项组成。其中，数据项建模了在t时刻某个目标的位置与所对应运动轨迹的相似度；平滑项表示相邻目标之间的相似度；标签项则用来规定合理轨迹所需要满足的多元化约束条件。联合求解方式结合递归的方式进行，进而在实现能量函数最小化近似求解的同时实现最优轨迹组合的选择。

4.3. 连续轨迹模型

跟多目标跟踪的纯粹的离散方法对比，我们使用三次B样条来表示连续空间的个人轨迹，三次B样条适合表示在现实世界中的场景，因为它可以避免离散化的轨迹，并提供了模型之间权衡模型的灵活性和内在的运动平滑。轨迹样条描述了在t时刻轨迹上每个目标的位置，我们假设样条有不同数量的控制点，并参数化矩阵，有利于明确每条轨迹起点和终点，但是往往倾向于呈现出极端值，导致极不可能的运动轨迹出现，为了确保样条不在起点和终点以外采取极端值，在每一个边界加一个Δ，防止相邻帧的其他检测目标属于轨迹。假设我们已经给出了数据关联，我们可以制定能量最小化的轨迹估计问题如下方程(1)：

$E_f^{te}\left(T\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(E_f^{te}\left(T_i\right)+\widehat{E_v^{te}}\left(T_i\right)\right)}$ (1)

$E_f^{te}\left(T_i\right)={\displaystyle \underset{t=s_i}{\overset{e_i}{\sum }}{\displaystyle \underset{j=1}{\overset{\left|D^t\right|}{\sum }}\delta \left[i-f_{d_j^t}\right]}}\cdot c_j^t\cdot {\Vert p_j^t-T_i\left(t\right)\Vert }^2$ (2)

如式(2)，对于每一个轨迹，我们的目标是最大限度地减少所有在有效图像帧的每个目标假设的欧式距离， $\left|D^t\right|$ 表示在t时刻里的目标数量， $\delta \left[a-b\right]$ 表示当a = b时值为1，否则为0。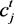表示t时刻j目标对应的置信度， ${\Vert p_j^t-T_i\left(t\right)\Vert }^2$ 表示目标实际距离与轨迹上的对应点的欧式距离。

$\widehat{E_v^{te}}\left(T_i\right)={\displaystyle \underset{\begin{array}{l}{s}_i-△\le t<s_i\\ e_i<t\le e_i+△\end{array}}{\sum }{\Vert v_i^t-T_i\left(t\right)\Vert }^2}$ (3)

${\Vert v_i^t-T_i\left(t\right)\Vert }^2$ 表示通过线性外推得到的虚拟位置V与轨迹上的对应点的欧式距离。Δ表示安全边界，一般取2。三次样条的目的是方便最大限度的能量最小化，在全局封闭的形式下解决最小二乘法问题。

4.4. 离散数据关联

数据关联往往是多目标跟踪最具挑战性的一个方面。我们制定一个利用强大的离散优化方法的多标签问题，实现离散成对的马尔可夫随机场的能量最小化。给出离散成对的马尔可夫随机场的能量最小化的方程：

$E_T^{da}\left(f\right)={\displaystyle \underset{d\in D}{\sum }{U}_d\left(f_d,T\right)}+{\displaystyle \underset{\left(d,d^{\prime }\right)\in E}{\sum }{S}_{d,d^{\prime }}\left(f_d,f_{d^{\prime }},G_d,G_{d^{\prime }}\right)}$ (4)

在式(4)中，数据项建模了t时刻第j个目标的位置与运动轨迹的相似度，用目标位置与其相关轨迹的欧氏距离和该目标的置信度乘积来表示，如式(5)。

$U_{d_j^t}\left(l,T\right)=c_j^t\cdot {\Vert p_j^t-T_l\left(y\right)\Vert }^2$ (5)

平滑项代表了相邻目标之间的相似度，本文中结合了组的信息G，平滑项定义将有权重矩阵 $W\left(d,d^{\prime },G_d,G_{d^{\prime }}\right)$ 和标签矩阵 $L\left(f_d,f_{d^{\prime }}\right)$ 两部分相乘得到，如式(6)。

$S_{d,d^{\prime }}\left(f_d,f_{d^{\prime }},G_d,G_{d^{\prime }}\right)=\eta \cdot W\left(d,d^{\prime },G_d,G_{d^{\prime }}\right)\cdot L\left(f_d,f_{d^{\prime }}\right)$ (6)

在式(6)中， $L\left(f_d,f_{d^{\prime }}\right)=\delta \left[f_{d_j^t}-f_{d_k^{t+1}}\right]$ 在时域上利用了Potts模型对相邻帧的目标标签 $f_{d_j^t}$ 和 $f_{d_j^{t+1}}$ 的一致性进行建模。对于 $W\left(d,d^{\prime },G_d,G_{d^{\prime }}\right)$ 式子，在多目标跟踪过程中，多个邻近的目标之间常见以组的形式进行运动，组内的每个目标之间通常满足较近的间距以及相似的运动速度和运动方向，本项目在基于运动分析的目标检测结果和带有噪声的目标轨迹基础上，对组的定义提出一种时域空域聚类方法，该方法能在较长的时间段内将具有相似速度且走得较近的多个目标划分到同一组中，利用聚类得到群组的信息可以在空域时域上提供相邻目标和轨迹之间的语义约束，从而有助于减少在多目标跟踪所带来的误差。其定义如式(7)所示，规定了当相邻图像帧的目标 $d_j^t$ 和 $d_j^{t+1}$ 对应的组 $G_{d_j^t}$ 和 $G_{d_k^{t+1}}$ 为同一个组时，他们运动的速度 $v_j^t$ 和 $v_k^{t+1}$ 以及方向 $o_j^t$ 和 $o_k^{t+1}$ 需要尽可能接近。

$W\left(d,d^{\prime },G_d,G_{d^{\prime }}\right)=\{\begin{array}{l}\exp \left(-\left({\Vert v_j^t-v_k^{t+1}\Vert }^2+{\Vert o_j^t-o_k^{t+1}\Vert }^2\right)/{\psi }^2\right),\text{if}{G}_{d_j^t}=G_{d_k^{t+1}}\\ const,\text{otherwise}\end{array}$ (7)

在构建基于时域-空域图时，将时域上的j目标检测看作图中的节点，只有满足时域上运动距离变化要求的节点之间才用边进行连接，如图2所示。

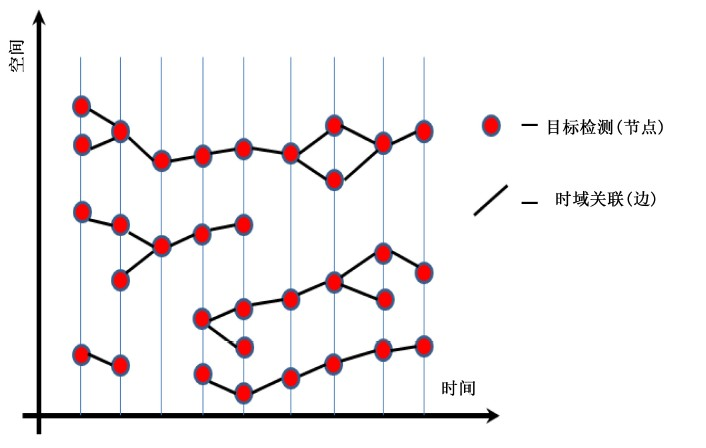
Figure 2. Time domain and airspace connection diagram

图2. 时域-空域连接图

4.5. 标签成本的离散连续跟踪

由于轨迹估计和数据关联方程的制定完成，接下来通过递归的方式最小化能量函数来实现数据关联和轨迹预测的同步优化求解。能量函数由数据项、平滑项和多个标签成本约束项组成，如式(8)。其中，数据项建模了在t时刻某个目标的位置与所对应运动轨迹的相似度；平滑项表示相邻目标之间的相似度；标签项则用来规定合理轨迹所需要满足的多元化约束条件。上述联合求解的方式在原有图切割的基础上结合递归的方式进行，进而在实现能量函数最小化近似求解的同时实现最优轨迹组合的选择。

$E\left(T,f\right)=\underset{数据项}{\underset{︸}{{\displaystyle \underset{d\in D}{\sum }{U}_d\left(f_d,T\right)}}}+\underset{平滑项}{\underset{︸}{{\displaystyle \underset{\left(d,d^{\prime }\right)\in E}{\sum }{S}_{d,d^{\prime }}\left(f_d,f_{d^{\prime }},g_d,g_{d^{\prime }}\right)}}}+\underset{标签项}{\underset{︸}{k\cdot h_f\left(T\right)}}$ (8)

标签项将用来实现轨迹的规范化。主要包含了一下五个标签代价函数，如式(9)：

$h_f\left(T\right)={\displaystyle \underset{\begin{array}{l}i=1\\ \exists d:f_d=i\end{array}}{\overset{N}{\sum }}{h}_i^{dyn}+h_i^{per}+h_i^{fid}+h_i^{col}+h_i^{reg}}$ (9)

1) $h_i^{dyn}$ ：由于现实世界中目标速度受物理约束的限制，对速度影响最大的样条曲线的三次系数施加一个惩罚。其定义如式(10)所示。

$h_i^{dyn}=\lambda \cdot \underset{r}{\max }{C}_i\left(r,1\right)$ (10)

2) $h_i^{per}$ ：执行长而且持久的轨迹来避免不必要的ID交换是关键，通过样条曲线，使我们能够确定每一个轨迹的开始和结束点，并对那些起点和终点均远离图像边界的轨迹进行惩罚。如式(11)，其中，和分别代表第条轨迹的起点和终点，而则代表到图像边界的距离运算。

$h_i^{per}=\mu \cdot \left(\bar{b}\left({\tau }_i\left(s_i\right)\right)+\bar{b}\left({\tau }_i\left(e_i\right)\right)\right)+v\cdot {\left(e_i-s_i\right)}^{-1}$ (11)

3) $h_i^{fid}$ ：表示高阶数据保真度，数据项鼓励轨迹附近的检测，以更好地解释所观察到的图像证据，如式(12)，其中，代表满足上述条件的轨迹中所具有的图像帧数。

$h_i^{fid}=\xi \cdot {\displaystyle \underset{k}{\sum }{\left|G_k\right|}^3}$ (12)

4) $h_i^{col}$ ：表示相互排斥性，如果2个假定的目标位置是彼此接近，加上一个高的罚款，除非至少有一个被标记为离群值在他们最接近的时间，最接近的每个人最小距离的计算和用于定义的标签成本。如式(13)，表示两个轨迹的时间重叠。

$h_i^{col}=\zeta \cdot {\left(\underset{j<i}{\min }\underset{t\in O}{\min }\Vert T_i\left(t\right)-T_j\left(t\right)\Vert \right)}^{-1}$ (13)

5) $h_i^{reg}$ ：一个固定的正则化成本 $h_i^{reg}=1$ 用来惩罚大量存在的轨迹。

在联合求解过程中，最小化能量函数的方式可通过递归的方式进行：首先，在结合标签代价函数的基础上通过传统的图切割实现数据关联的近似最优解；其次，根据数据关联的结果来实现连续轨迹的拟合。上述过程将递归地进行直到能量收敛到全局最小，从而得到优化后的数据关联和轨迹预测结果 [17]。

5. 实验结果与分析

在本文中，我们采用了PETS 2009/2010 benchmark里的S1L1序列以及UCY Computer Graphics Lab里的“Crowds-by-Example”的Zara Data Set分别评价本文的群组分析和连续离散问题联合求解，并采用Zara Data Set来展现与 [17]中算法的效果比较。

图3给出了本文算法在PETS 09 S1L1数据集100帧内下以相同颜色的矩形框表示属于同一组的群组聚类结果。可以看出图像帧中的相似运动方向以及速度的目标群体会判定为同一组，并且稳定存在。图中黑色椭圆框住的目标与图像中大多数目标行动方向一直保持相反，在本文算法中始终判定为孤立组，可以很好地说明本文算法群组聚类的稳定性。通过上述方法，可以实现目标时域空域内的聚类。

本文利用连续离散联合求解的框架在目标数量密集且以群组运动的Zara数据集上运行。

如图4，在第41帧图像中出现一个红色矩形框，但是该区域并没有目标出现，通过第54帧和61帧图像中可以发现粉红色矩形框被红色矩形框替代，原因是系统判定目标相交时发生了身份交换，在第72帧和第80帧图像中可以比较出相邻的两个目标发生了身份交换，由此我们可以发现连续离散联合求解框架在目标数量不多且较分散时跟踪精度较高，但是在行人共进或者发生相交的时候会变得不够稳定。由此本文创新性地提出基于群组分析的多目标跟踪，在原有的基础框架上增加新的约束，提高多目标跟踪的精度。

Figure 3. Group clustering results for PETS 09 S1L1 dataset

图3. PETS 09 S1L1下的群组聚类结果

Figure 4. Tracking results of the [17]algorithm in the Zara Data Set dataset

图4. [17]中算法Zara Data Set数据集中的跟踪结果

Figure 5. Tracking results of our algorithm in the Zara Data Set dataset

图5. 本文算法在Zara数据集下的多目标跟踪结果

如图5，与图4之间比较，第54帧与第61帧中由于群组分析的约束，两条轨迹保持一定的稳定性，没有发生身份交换，并以合理正确的轨迹前进。第72帧与第80帧中黑色椭圆框住的两个目标在 [17]算法中是发生了身份交换，在本文的算法中群组约束起到了一定的作用，没有发生身份交换，实现了正确的轨迹跟踪。

6. 结束语

本文所研究的多目标跟踪技术不仅能对场景中的多位目标进行定位和长时间跟踪，而且还可应用于室内外场景的自主监控，可有效地应用于目标跟踪定位、突发事件预防等方面，从而实现传统安防的技术进一步智能化。本文所提出的算法将数据关联和轨迹预测两个不同但紧密关联的问题融合到统一的框架中实现联合求解，并在此基础上创新性地提出群组的行为分析，有效地改善多目标跟踪的性能。此外，还能将此项目成果结合其他相关技术完成其他目标，实现了技术的推广。

基金项目

王伟明助创基金项目(2016007)；2016年度宁波工程学院学生科研项目；浙江省公益技术应用研究计划项目(2016C33255)；浙江省重点研发计划项目(2018C01086)。